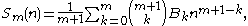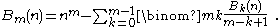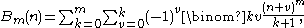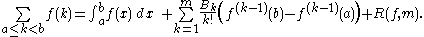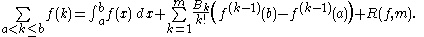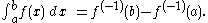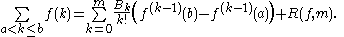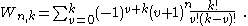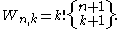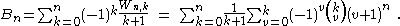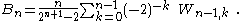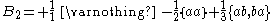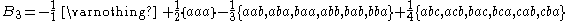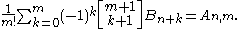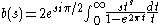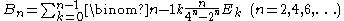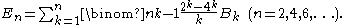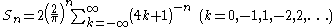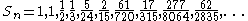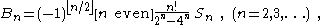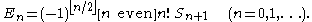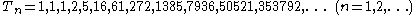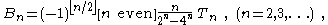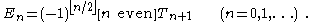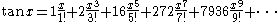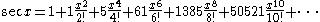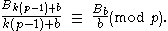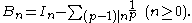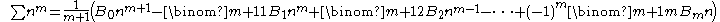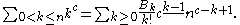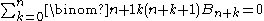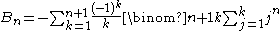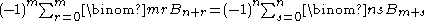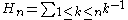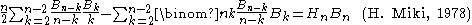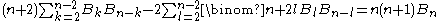Bernoulli number
Encyclopedia
In mathematics
, the Bernoulli numbers Bn are a sequence
of rational number
s with deep connections to number theory
. They are closely related to the values of the Riemann zeta function at negative integers.
There are several conventions for Bernoulli numbers. The most common has Bn = 0 for all odd n other than 1, and B1 = −1/2, but some authors use B1 = +1/2 and some write Bn for B2n. The values of the first few nonzero Bernoulli numbers are (more values below):
The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jakob Bernoulli, after whom they are named, and independently by Japanese mathematician Seki Kōwa. Seki's discovery was posthumously published in 1712 in his work Katsuyo Sampo; Bernoulli's, also posthumously, in his Ars Conjectandi
of 1713.
They appear in the Taylor series
expansions of the tangent and hyperbolic tangent
functions, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.
In note G of Ada Lovelace's
notes on the analytical engine
from 1842, Lovelace describes an algorithm
for generating Bernoulli numbers with Babbage's
machine. As a result, the Bernoulli numbers have the distinction of being the subject of the first computer program
.
of the sum of powers for fixed values of m
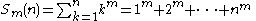
are always polynomial
s in n of degree m + 1. Note that Sm(0) = 0 for all m ≥ 0 because in this case the sum is the empty sum
. The coefficient
s of these polynomials are related to the Bernoulli numbers by Bernoulli's formula:
where B1 = +1/2.
Let n ≥ 0. Taking m to be 0 and B0 = 1 gives the natural number
s 0, 1, 2, 3, ... .
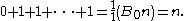
Taking m to be 1 and B1 = 1/2 gives the triangular number
s 0, 1, 3, 6, ... .
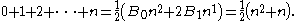
Taking m to be 2 and B2 = 1/6 gives the square pyramidal number
s 0, 1, 5, 14, ... .
Some authors state Bernoulli's formula in a different way:
where B1 = −1/2. In the next section consequences of the resulting differences will be commented on as they are likely to produce some confusion.
Bernoulli's formula is sometimes called Faulhaber's formula after Johann Faulhaber
who also found remarkable ways to calculate sum of powers.
Faulhaber's formula was generalized by V. Guo and J. Zeng to a q-analog
.
For the proof of the equivalence
of the four approaches the reader is referred to mathematical expositions like or .
Unfortunately in the literature the definition is given in two variants: Despite the fact that Bernoulli defined B1 = 1/2, some authors set B1 = −1/2 (more on different conventions below). In order to prevent potential confusions both variants will be described here, side by side.
This equation defines rational numbers Bm(n) for all integers n ≥ 0, m ≥ 0. 00 has to be interpreted as 1. The recursion has its base in B0(n) = 1 for all n. The two variants now follow by setting n = 0 respectively n = 1. Additionally the notation is simplified by erasing the reference to the parameter n.Iverson bracket). Whenever a confusion between the two kinds of definitions might arise it can be avoided by referring to the more general definition and by reintroducing the erased parameter: writing Bm(0) in the first case and Bm(1) in the second will unambiguously denote the value in question.Vandiver's conjecture holds for p, or even just to determine whether p is an irregular prime. It is not feasible to carry out such a computation using the above recursive formulae, since at least (a constant multiple of) p2 arithmetic operations would be required. Fortunately, faster methods have been developed which require only O(p (log p)2) operations (see big-O notation).
Each of these viewpoints leads to a set of more or less different conventions.
This formulation assumes the convention B1 = −1/2. However, if one sets B1 = 1/2 then this formula can also be written as
Here ƒ(0) = ƒ which is a commonly used notation identifying the zero-th derivative of ƒ with ƒ. Moreover, let ƒ(−1) denote an antiderivative
of ƒ. By the fundamental theorem of calculus
,
Thus the last formula can be further simplified to the following succinct form of the Euler–Maclaurin formula
This form is for example the source for the important Euler–MacLaurin expansion of the zeta function (B1 = 1/2)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bernoulli numbers Bn are a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s with deep connections to number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. They are closely related to the values of the Riemann zeta function at negative integers.
There are several conventions for Bernoulli numbers. The most common has Bn = 0 for all odd n other than 1, and B1 = −1/2, but some authors use B1 = +1/2 and some write Bn for B2n. The values of the first few nonzero Bernoulli numbers are (more values below):
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bn | 1 | −1/2 | 1/6 | 0 | −1/30 | 0 | 1/42 | 0 | −1/30 | 0 | 5/66 | 0 | −691/2730 | 0 | 7/6 |
The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jakob Bernoulli, after whom they are named, and independently by Japanese mathematician Seki Kōwa. Seki's discovery was posthumously published in 1712 in his work Katsuyo Sampo; Bernoulli's, also posthumously, in his Ars Conjectandi
Ars Conjectandi
Ars Conjectandi is a combinatorial mathematical paper written by Jakob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, most notably among other combinatorial topics, probability theory: indeed, it is widely regarded as...
of 1713.
They appear in the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansions of the tangent and hyperbolic tangent
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
functions, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.
In note G of Ada Lovelace's
Ada Lovelace
Augusta Ada King, Countess of Lovelace , born Augusta Ada Byron, was an English writer chiefly known for her work on Charles Babbage's early mechanical general-purpose computer, the analytical engine...
notes on the analytical engine
Analytical engine
The Analytical Engine was a proposed mechanical general-purpose computer designed by English mathematician Charles Babbage. It was first described in 1837 as the successor to Babbage's difference engine, a design for a mechanical calculator...
from 1842, Lovelace describes an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for generating Bernoulli numbers with Babbage's
Charles Babbage
Charles Babbage, FRS was an English mathematician, philosopher, inventor and mechanical engineer who originated the concept of a programmable computer...
machine. As a result, the Bernoulli numbers have the distinction of being the subject of the first computer program
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
.
Sum of powers
Closed formsClosed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
of the sum of powers for fixed values of m
are always polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in n of degree m + 1. Note that Sm(0) = 0 for all m ≥ 0 because in this case the sum is the empty sum
Empty sum
In mathematics, an empty sum, or nullary sum, is a summation involving no terms at all. The value of any empty sum of numbers is conventionally taken to be zero...
. The coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s of these polynomials are related to the Bernoulli numbers by Bernoulli's formula:
where B1 = +1/2.
Let n ≥ 0. Taking m to be 0 and B0 = 1 gives the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s 0, 1, 2, 3, ... .
Taking m to be 1 and B1 = 1/2 gives the triangular number
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
s 0, 1, 3, 6, ... .
Taking m to be 2 and B2 = 1/6 gives the square pyramidal number
Square pyramidal number
In mathematics, a pyramid number, or square pyramidal number, is a figurate number that represents the number of stacked spheres in a pyramid with a square base...
s 0, 1, 5, 14, ... .
Some authors state Bernoulli's formula in a different way:
-
,
where B1 = −1/2. In the next section consequences of the resulting differences will be commented on as they are likely to produce some confusion.
Bernoulli's formula is sometimes called Faulhaber's formula after Johann Faulhaber
Johann Faulhaber
Johann Faulhaber was a German mathematician.Born in Ulm, Faulhaber trained as a weaver and later took the role of a surveyor of the city of Ulm. He collaborated with Johannes Kepler and Ludolph van Ceulen...
who also found remarkable ways to calculate sum of powers.
Faulhaber's formula was generalized by V. Guo and J. Zeng to a q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
.
Definitions
Many characterizations of the Bernoulli numbers have been found in the last 300 years, and each could be used to introduce these numbers. Here only four of the most useful ones are mentioned:- a recursive equation,
- an explicit formula,
- a generating function,
- an algorithmic description.
For the proof of the equivalence
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
of the four approaches the reader is referred to mathematical expositions like or .
Unfortunately in the literature the definition is given in two variants: Despite the fact that Bernoulli defined B1 = 1/2, some authors set B1 = −1/2 (more on different conventions below). In order to prevent potential confusions both variants will be described here, side by side.
Recursive definition
The recursive equation is best introduced in a slightly more general form
This equation defines rational numbers Bm(n) for all integers n ≥ 0, m ≥ 0. 00 has to be interpreted as 1. The recursion has its base in B0(n) = 1 for all n. The two variants now follow by setting n = 0 respectively n = 1. Additionally the notation is simplified by erasing the reference to the parameter n.
| Computer | Year | n | Digits* |
|---|---|---|---|
| J. Bernoulli | ~1689 | 10 | 1 |
| L. Euler | 1748 | 30 | 8 |
| J.C. Adams | 1878 | 62 | 36 |
| D.E. Knuth, T.J. Buckholtz | 1967 | 1672 | 3330 |
| G. Fee, S. Plouffe | 1996 | 10000 | 27677 |
| G. Fee, S. Plouffe | 1996 | 100000 | 376755 |
| B.C. Kellner | 2002 | 1000000 | 4767529 |
| O. Pavlyk | 2008 | 10000000 | 57675260 |
| D. Harvey | 2008 | 100000000 | 676752569 |
- Digits is to be understood as the exponent of 10 when B(n) is written as a real in normalized scientific notationScientific notationScientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...
.
Different viewpoints and conventions
The Bernoulli numbers can be regarded from four main viewpoints:- as standalone arithmetical objects,
- as combinatorial objects,
- as values of a sequence of certain polynomials,
- as values of the Riemann zeta function.
Each of these viewpoints leads to a set of more or less different conventions.
Bernoulli numbers as standalone arithmetical objects.
Associated sequence: 1/6, −1/30, 1/42, −1/30,...
This is the viewpoint of Jakob Bernoulli. (See the cutout from his Ars Conjectandi, first edition, 1713). The Bernoulli numbers are understood as numbers, recursive in nature, invented to solve a certain arithmetical problem, the summation of powers, which is the paradigmatic application of the Bernoulli numbers. It is misleading to call this viewpoint 'archaic'. For example Jean-Pierre SerreJean-Pierre SerreJean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
uses it in his highly acclaimed book A Course in Arithmetic which is a standard textbook used at many universities today.
Bernoulli numbers as combinatorial objects.
Associated sequence: 1, +1/2, 1/6, 0,....
This view focuses on the connection between Stirling numbers and Bernoulli numbers and arises naturally in the calculus of finite differences. In its most general and compact form this connection is summarized by the definition of the Stirling polynomials σn(x), formula (6.52) in Concrete Mathematics by Graham, Knuth and Patashnik.
In consequence Bn = n! σn(1) for n ≥ 0.
-
Bernoulli numbers as values of a sequence of certain polynomials.
Assuming the Bernoulli polynomials as already introduced
the Bernoulli numbers can be defined in two different ways:
Bn = Bn(0). Associated sequence: 1, −1/2, 1/6, 0,....
Bn = Bn(1). Associated sequence: 1, +1/2, 1/6, 0,....
The two definitions differ only in the sign of B1. The choice Bn = Bn(0) is the convention used in the Handbook of Mathematical Functions.
Bernoulli numbers as values of the Riemann zeta function.
Associated sequence: 1, +1/2, 1/6, 0,....
This convention agrees with the convention Bn = Bn(1) (for example J. Neukirch and M. Kaneko). The sign '+' for B1 matches the representation of the Bernoulli numbers by the Riemann zeta function. In fact the identity nζ(1 − n) = (−1)n+1Bn valid for all n > 0 is then replaced by the simpler nζ(1 − n) = −Bn. (See the paper of S. C. Woon.)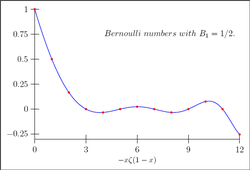
(Note that in the foregoing equation for n = 0 and n = 1 the expression −nζ(1 − n) is to be understood as limx → n −xζ(1 − x).)
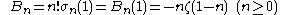
Asymptotic analysis
Arguably the most important application of the Bernoulli number in mathematics is their use in the Euler–MacLaurin formula. Assuming that ƒ is a sufficiently often differentiable function the Euler–MacLaurin formula can be written as
This formulation assumes the convention B1 = −1/2. However, if one sets B1 = 1/2 then this formula can also be written as
Here ƒ(0) = ƒ which is a commonly used notation identifying the zero-th derivative of ƒ with ƒ. Moreover, let ƒ(−1) denote an antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
of ƒ. By the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
,
Thus the last formula can be further simplified to the following succinct form of the Euler–Maclaurin formula
This form is for example the source for the important Euler–MacLaurin expansion of the zeta function (B1 = 1/2)
-
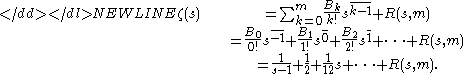
Here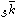
denotes the rising factorial power.
Bernoulli numbers are also frequently used in other kinds of asymptotic expansionAsymptotic expansionIn mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
s.
The following example is the classical Poincaré-type asymptotic expansion of the
digamma function (again B1 = 1/2).
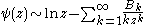
Use in topology
The Kervaire–Milnor formula for the order of the cyclic group of diffeomorphism classes of exotic (4n − 1)-spheresExotic sphereIn differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
which bound parallelizable manifolds involves Bernoulli numbers. Let ESn be the number of such exotic spheres for n ≥ 2, then (see also sequence )
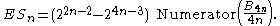
The Hirzebruch signature theorem for the L genus of a smooth orientedOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
closed manifoldClosed manifoldIn mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
of dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
4n also involves Bernoulli numbers.
Combinatorial definitions
The connection of the Bernoulli number to various kinds of combinatorial numbers is based on the classical theory of finite differences and on the combinatorial interpretation of the Bernoulli numbers as an instance of a fundamental combinatorial principle, the inclusion-exclusion principleInclusion-exclusion principleIn combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
.
Connection with Worpitzky numbers
The definition to proceed with was developed by Julius Worpitzky in 1883. Besides elementary arithmetic only the factorial function n! and the power function km is employed. The signless Worpitzky numbers are defined as
They can also be expressed through the Stirling numbers of the second kind
A Bernoulli number is then introduced as an inclusion-exclusion sum of Worpitzky numbers weighted by the sequence 1, 1/2, 1/3,...
This representation has B1 = 1/2.
Worpitzky's representation of the Bernoulli number
B0
=
1/1
B1
=
1/1 − 1/2
B2
=
1/1 − 3/2 + 2/3
B3
=
1/1 − 7/2 + 12/3 − 6/4
B4
=
1/1 − 15/2 + 50/3 − 60/4 + 24/5
B5
=
1/1 − 31/2 + 180/3 − 390/4 + 360/5 − 120/6
B6
=
1/1 − 63/2 + 602/3 − 2100/4 + 3360/5 − 2520/6 + 720/7
A second formula representing the Bernoulli numbers by the Worpitzky numbers is for n ≥ 1
Connection with Stirling numbers of the second kind
A similar combinatorial representation derives from
-
Here the Bernoulli numbers are an inclusion-exclusion over the set of length-n words, where the sum is taken over all words of length n with k distinct letters, and normalized by k + 1. The combinatorics of this representation can be seen from:
Connection with Stirling numbers of the first kind
The two main formulas relating the unsigned Stirling numbers of the first kindStirling numbers of the first kindIn mathematics, Stirling numbers of the first kind, together with the Stirling numbers of the second kind, are the two types of Stirling numbers. They commonly occur in combinatorics, where they appear in the study of permutations. The Stirling numbers of the first and second kind can be...
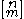to the Bernoulli numbers (with B1 = 1/2) are
and the inversion of this sum (for n ≥ 0, m ≥ 0)
Here the number An,m are the rational Akiyama–Tanigawa number, the first few of which are displayed in the following table.
Akiyama–Tanigawa number
n \ m
0
1
2
3
4
0
1 1/2 1/3 1/4 1/5
1
1/2 1/3 1/4 1/5 ...
2
1/6 1/6 3/20 ... ...
3
0 1/30 ... ... ...
4
−1/30 ... ... ... ...
The Akiyama–Tanigawa numbers satisfy a simple recurrence relation which can be exploited to iteratively compute the Bernoulli numbers. This leads to the algorithm
shown in the section 'algorithmic description' above.
Connection with Eulerian numbers
There are formulas connecting Eulerian numberEulerian numberIn combinatorics the Eulerian number A, is the number of permutations of the numbers 1 to n in which exactly m elements are greater than the previous element...
s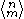
to Bernoulli numbers:
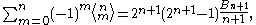
Both formulas are valid for n ≥ 0 if B1 is set to ½. If B1 is set to −½ they are valid only for n ≥ 1 and n ≥ 2 respectively.
A binary tree representation
The Stirling polynomials σn(x) are related to the Bernoulli
numbers by Bn = n!σn(1).
S. C. Woon described an algorithm to compute σn(1) as a binary
tree.
Woon's tree for σn(1)
Woon's recursive algorithm (for n ≥ 1) starts by assigning to the root node
N = [1,2]. Given a node N = [a1,a2,...,
ak] of the tree, the left child of the node is L(N) = [−a1,a2 + 1, a3, ..., ak] and the right child R(N) = [a1,2, a2, ..., ak].
Given a node N the factorial of N is defined as
Restricted to the nodes N of a fixed tree-level n the sum of 1/N! is σn(1), thus
For example B1 = 1!(1/2!), B2 = 2!(−1/3! + 1/(2!2!)), B3 = 3!(1/4! − 1/(2!3!) − 1/(3!2!) + 1/(2!2!2!)).
Asymptotic approximation
Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
expressed the Bernoulli numbers in terms of the Riemann zeta function as
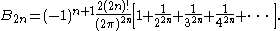
It then follows from the Stirling formula that, as n goes to infinity,
Including more terms from the zeta series yields a better approximation, as does factoring in the asymptotic series in Stirling's approximation.
Integral representation and continuation
The integralIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
has as special values b(2n) = B2n for n > 0. The integral might be considered as a continuation of the Bernoulli numbers to the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
and this was indeed suggested by Peter Luschny in 2004.
For example b(3) = (3/2)ζ(3)Π−3Ι and b(5) = −(15/2) ζ(5) Π −5Ι. Here ζ(n) denotes the Riemann zeta function and Ι the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. It is remarkable that already Leonhard Euler (Opera Omnia, Ser. 1, Vol. 10, p. 351) considered these numbers and calculated
Euler's values are unsigned and real, but obviously his aim was to find a meaningful way to define the Bernoulli numbers at the odd integers n > 1.
The relation to the Euler numbers and π
The Euler numbers are a sequence of integers intimately connected with the Bernoulli numbers. Comparing the
asymptotic expansions of the Bernoulli and the Euler numbers shows that the Euler numbers E2n are in magnitude approximately (2/π)(42n − 22n) times larger than the Bernoulli numbers B2n. In consequence:
This asymptotic equation reveals that π lies in the common root of both the Bernoulli and the Euler numbers. In fact π could be computed from these rational approximations.
Bernoulli numbers can be expressed through the Euler numbers and vice versa. Since for n odd Bn = En = 0 (with the exception B1), it suffices to consider the case when n is even.
These conversion formulas express an inverse relationInverse relationIn mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
between the Bernoulli and the Euler numbers. But more important, there is a deep arithmetic root common to both kinds of numbers, which can be expressed through a more fundamental sequence of numbers, also closely tied to π. These numbers are defined for n > 1 as
and S1 = 1 by convention . The magic of these numbers lies in the fact that they turn out to be rational numbers. This was first proved by Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in a landmark paper ‘De summis serierum reciprocarum’ (On the sums of series of reciprocals) and has fascinated mathematicians ever since. The first few of these numbers are
The Bernoulli numbers and Euler numbers are best understood as special views of these numbers, selected from the sequence Sn and scaled for use in special applications.
The expression [n even] has the value 1 if n is even and 0 otherwise (Iverson bracket).
These identities show that the quotient of Bernoulli and Euler numbers at the beginning of this section is just the special case of Rn = 2Sn / Sn+1 when n is even. The Rn are rational approximations to π and two successive terms always enclose the true value of π. Beginning with n = 1 the sequence starts
These rational numbers also appear in the last paragraph of Euler's paper cited above. But it was only in September 2007 that this classical sequence found its way into the Encyclopedia of Integer Sequences .
An algorithmic view: the Seidel triangle
The sequence Sn has another unexpected yet important property: The denominators of Sn divide the factorial (n − 1)! . In other words: the numbers Tn = Sn(n − 1)! are integers.
Thus the above representations of the Bernoulli and Euler numbers can be rewritten in terms of this sequence as
These identities make it easy to compute the Bernoulli and Euler numbers: the Euler numbers En are given immediately by T2n + 1 and the Bernoulli numbers B2n are obtained from T2n by some easy shifting, avoiding rational arithmetic.
What remains is to find a convenient way to compute the numbers Tn. However, already in 1877 Philipp Ludwig von SeidelPhilipp Ludwig von SeidelPhilipp Ludwig von Seidel was a German mathematician. His mother was Julie Reinhold and his father was Justus Christian Felix Seidel.Lakatos credits von Seidel with discovering, in 1847, the crucial analytic concept of uniform convergence, while analyzing an incorrect proof of Cauchy's.In 1857,...
published an ingenious algorithm which makes it extremely simple to calculate Tn.
Seidel's algorithm for Tn
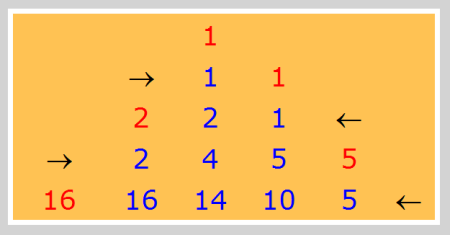
[begin] Start by putting 1 in row 0 and let k denote the number of the row currently being filled. If k is odd, then put the number on the left end of the row k − 1 in the first position of the row k, and fill the row from the left to the right, with every entry being the sum of the number to the left and the number to the upper. At the end of the row duplicate the last number. If k is even, proceed similar in the other direction. [end]
Seidel's algorithm is in fact much more general (see the exposition of Dominique Dumont ) and was rediscovered several times thereafter.
Similar to Seidel's approach D. E. Knuth and T. J. Buckholtz gave a recurrence equation for the numbers T2n and recommended this method for computing B2n and E2n ‘on electronic computers using only simple operations on integers’.
V. I. Arnold rediscovered Seidel's algorithm in and later Millar, Sloane and Young popularized Seidel's algorithm under the name boustrophedon transformBoustrophedon transformIn mathematics, the boustrophedon transform is a procedure which maps one sequence to another. The transformed sequence is computed by filling a triangular array in boustrophedon manner.-Definition:...
.
A combinatorial view: alternating permutations
Around 1880, three years after the publication of Seidel's algorithm, Désiré André proved a now classic result of combinatorial analysis & . Looking at the first terms of the Taylor expansion of the trigonometric functions
tan x and sec x André made a startling discovery.
The coefficients are the Euler numbers of odd and even index, respectively. In consequence the ordinary expansion of tan x + sec x has as coefficients the rational numbers Sn.
André then succeeded by means of a recurrence argument to show that the alternating permutations of odd size are enumerated by the Euler numbers of odd index (also called tangent numbers) and the alternating permutations of even size by the Euler numbers of even index (also called secant numbers).
Generalizations by polynomials
The Bernoulli polynomialsBernoulli polynomialsIn mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
can be regarded as generalizations of the Bernoulli numbers the same as the Euler polynomials are generalizations of the Euler numbers.
Arithmetical properties of the Bernoulli numbers
The Bernoulli numbers can be expressed in terms of the Riemann zeta function as Bn = − nζ(1 − n) for integers n ≥ 0 provided for n = 0 and n = 1 the expression − nζ(1 − n) is understood as the limiting value and the convention B1 = 1/2 is used. This intimately relates them to the values of the zeta function at negative integers. As such, they could be expected to have and do have deep arithmetical properties. For example, the Agoh–Giuga conjecture postulates that p is a prime number if and only if pBp−1 is congruent to −1 modulo p. Divisibility properties of the Bernoulli numbers are related to the ideal class groupIdeal class groupIn mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
s of cyclotomic fieldCyclotomic fieldIn number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
s by a theorem of Kummer and its strengthening in the Herbrand-Ribet theorem, and to class numbers of real quadratic fields by Ankeny–Artin–Chowla.
The Kummer theorems
The Bernoulli numbers are related to Fermat's last theoremFermat's Last TheoremIn number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
(FLT) by KummerErnst KummerErnst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
's theorem , which says:
If the odd prime p does not divide any of the numerators of the Bernoulli numbers B2, B4, ..., Bp−3 then xp + yp + zp = 0 has no solutions in non-zero integers.
Prime numbers with this property are called regular primes. Another classical result of Kummer are the following congruences.
Let p be an odd prime and b an even number such that p − 1 does not divide b. Then for any non-negative integer k
A generalization of these congruences goes by the name of p-adic continuity.
p-adic continuity
If b, m and n are positive integers such that m and n are not divisible by p − 1 and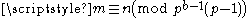
, then
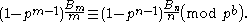
Since Bn = —n ζ(1 — n), this can also be written
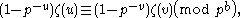
where u = 1 − m and v = 1 − n, so that u and v are nonpositive and not congruent to 1 modulo p − 1. This tells us that the Riemann zeta function, with 1 − p−s taken out of the Euler product formula, is continuous in the p-adic numberP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s on odd negative integers congruent modulo p − 1 to a particular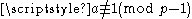
, and so can be extended to a continuous function ζp(s) for all p-adic integers 
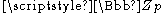, the p-adic zeta function.
Ramanujan's congruences
The following relations, due to Ramanujan, provide a more efficient method for calculating Bernoulli numbers:
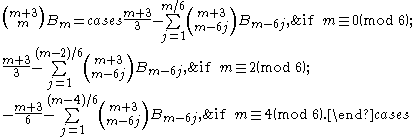
Von Staudt–Clausen theorem
The von Staudt–Clausen theoremVon Staudt–Clausen theoremIn number theory, the von Staudt–Clausen theorem is a result determining the fractional part of Bernoulli numbers, found independently by and ....
was given by Karl Georg Christian von StaudtKarl Georg Christian von StaudtKarl Georg Christian von Staudt was a German mathematician born in the Free Imperial City of Rothenburg, which is now called Rothenburg ob der Tauber in Germany. From 1814 he studied in Gymnasium in Ausbach. He attended the University of Göttingen from 1818 to 1822 where he studied with Gauss who...
and Thomas ClausenThomas Clausen (mathematician)Thomas Clausen was a Danish mathematician and astronomer....
independently in 1840. The theorem affirms the existence of a number In. which is either an integer or , such that
The sum is over the primes p for which p − 1 divides n. These are the same primes which are employed in the Clausen algorithm. The proposition holds true for all n > 0, not only for even n. I1 = 1 and for odd n > 1, In = (and I2n is always an integer).
A consequence of the von Staudt–Clausen theorem is: the denominators of the Bernoulli numbers are square-free and for n ≥ 2 divisible by 6.
Why do the odd Bernoulli numbers vanish?
The sum
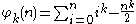
can be evaluated for negative values of the index n. Doing so will show that it is an odd function for even values of k, which implies that the sum has only terms of odd index. This and the formula for the Bernoulli sum imply that B2k+1−m is 0 for m odd and greater than 1; and that the term for B1 is cancelled by the subtraction. The von Staudt Clausen theorem combined with Worpitzky's representation also gives a combinatorial answer to this question (valid for n > 1).
From the von Staudt Clausen theorem it is known that for odd n > 1 the number 2Bn is an integer. This seems trivial if one knows beforehand that in this case Bn = 0. However, by applying Worpitzky's representation one gets
-
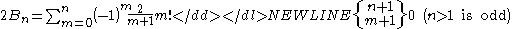
as a sum of integers, which is not trivial. Here a combinatorial fact comes to surface which explains the vanishing of the Bernoulli numbers at odd index. Let Sn,m be the number of surjective maps from {1, 2, ..., n} to {1, 2, ..., m}, then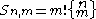
. The last equation can only hold if
This equation can be proved by induction. The first two examples of this equation are
- n = 4: 2 + 8 = 7 + 3,
- n = 6: 2 + 120 + 144 = 31 + 195 + 40.
Thus the Bernoulli numbers vanish at odd index because some non-obvious combinatorial identities are embodied in the Bernoulli numbers.
A restatement of the Riemann hypothesis
The connection between the Bernoulli numbers and the Riemann zeta function is strong enough to provide an alternate formulation of the Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
(RH) which uses only the Bernoulli number. In fact Marcel RieszMarcel RieszMarcel Riesz was a Hungarian mathematician who was born in Győr, Hungary . He moved to Sweden in 1908 and spent the rest of his life there, dying in Lund, where he was a professor from 1926 at Lund University...
proved that the RH is equivalent to the following assertion:
For every ε > 1/4 there exists a constant Cε > 0 (depending on ε) such that |R(x)| < Cε xε as x → ∞.
Here R(x) is the Riesz function
-
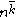denotes the rising factorial power in the notation of D. E. Knuth. The number βn = Bn/n occur frequently in the study of the zeta function and are significant because βn is a p-integer for primes p where p − 1 does not divide n. The βn are called divided Bernoulli number.
Early history
The Bernoulli numbers are rooted in the early history of the computation of sums of integer powers, which have been of interest to mathematicians since antiquity.
Methods to calculate the sum of the first n positive integers, the sum of the squares and of the cubes of the first n positive integers were known, but there were no real 'formulas', only descriptions given entirely in words. Among the great mathematicians of antiquity which considered this problem were: Pythagoras
PythagorasPythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
(c. 572–497 BCE, Greece), ArchimedesArchimedesArchimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
(287–212 BCE, Italy), AryabhataAryabhataAryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
(b. 476, India), Abu Bakr al-Karaji (d. 1019, Persia) and Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham (965–1039, Egypt).
During the late sixteenth and early seventeenth centuries mathematicians made significant progress. In the West Thomas HarriotThomas HarriotThomas Harriot was an English astronomer, mathematician, ethnographer, and translator. Some sources give his surname as Harriott or Hariot or Heriot. He is sometimes credited with the introduction of the potato to Great Britain and Ireland...
(1560–1621) of England, Johann FaulhaberJohann FaulhaberJohann Faulhaber was a German mathematician.Born in Ulm, Faulhaber trained as a weaver and later took the role of a surveyor of the city of Ulm. He collaborated with Johannes Kepler and Ludolph van Ceulen...
(1580–1635) of Germany, Pierre de FermatPierre de FermatPierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
(1601–1665) and fellow French mathematician Blaise PascalBlaise PascalBlaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
(1623–1662) all played important roles.
Thomas Harriot seems to have been the first to derive and write formulas for sums of powers using symbolic notation, but even he calculated only up to the sum of the fourth powers. Johann Faulhaber gave formulas for sums of powers up to the 17th power in his 1631 Academia Algebrae, far higher than anyone before him, but he did not give a general formula.
The Swiss mathematician Jakob Bernoulli (1654–1705) was the first to realize the existence of a single sequence of constants B0, B1, B2, ... which provide a uniform formula for all sums of powers .
The joy Bernoulli experienced when he hit upon the pattern needed to compute quickly and easily the coefficients of his formula for the sum of the c-th powers for any positive integer c can be seen from his comment. He wrote:
“With the help of this table, it took me less than half of a quarter of an hour to find that the tenth powers of the first 1000 numbers being added together will yield the sum
91,409,924,241,424,243,424,241,924,242,500.”
Bernoulli's result was published posthumously in Ars ConjectandiArs ConjectandiArs Conjectandi is a combinatorial mathematical paper written by Jakob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, most notably among other combinatorial topics, probability theory: indeed, it is widely regarded as...
in 1713. Seki Kōwa independently discovered the Bernoulli numbers and his result was published a year earlier, also posthumously, in 1712. However, Seki did not present his method as a formula based on a sequence of constants.
Bernoulli's formula for sums of powers is the most useful and generalizable formulation to date. The coefficients in Bernoulli's formula are now called Bernoulli numbers, following a suggestion of Abraham de MoivreAbraham de MoivreAbraham de Moivre was a French mathematician famous for de Moivre's formula, which links complex numbers and trigonometry, and for his work on the normal distribution and probability theory. He was a friend of Isaac Newton, Edmund Halley, and James Stirling...
.
Bernoulli's formula is sometimes called Faulhaber's formula after Johann Faulhaber who found remarkable ways to calculate sum of powers but never stated Bernoulli's formula. To call Bernoulli's formula Faulhaber's formula does injustice to Bernoulli and simultaneously hides the genius of Faulhaber as Faulhaber's formula is in fact more efficient than Bernoulli's formula. According to Knuth a rigorous proof of Faulhaber’s formula was first published by Carl Jacobi in 1834 . Donald E. Knuth's in-depth study of Faulhaber's formula concludes:
“Faulhaber never discovered the Bernoulli numbers; i.e., he never realized that a single sequence of constants B0, B1, B2, ... would provide a uniform
for all sums of powers. He never mentioned, for example, the fact that almost half of the coefficients turned out to be zero after he had converted his formulas for
from polynomials in N to polynomials in n.”
Reconstruction of 'Summae Potestatum'
The Bernoulli numbers were introduced by Jakob Bernoulli in the book Ars Conjectandi
Ars ConjectandiArs Conjectandi is a combinatorial mathematical paper written by Jakob Bernoulli and published in 1713, eight years after his death, by his nephew, Niklaus Bernoulli. The seminal work consolidated, most notably among other combinatorial topics, probability theory: indeed, it is widely regarded as...
published posthumously in 1713. The main formula can be seen in the second half of the corresponding facsimile. The constant coefficients denoted A, B, C and D by Bernoulli are mapped to the notation which is now prevalent as A = B2, B = B4, C = B6, D = B8. In the expression c·c−1·c−2·c−3 the small dots are used as grouping symbols, not as signs for multiplication. Using today's terminology these expressions are falling factorial powers
. The factorial notation k! as a shortcut for 1 × 2 × ... × k was not introduced until 100 years later. The integral symbol on the left hand side goes back to Gottfried Wilhelm Leibniz in 1675 who used it as a long letter S for "summa" (sum). (The Mathematics Genealogy Project
shows Leibniz as the doctoral adviser of Jakob Bernoulli. See also the Earliest Uses of Symbols of Calculus.) The letter n on the left hand side is not an index of summationSummationSummation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
but gives the upper limit of the range of summation which is to be understood as 1, 2, …, n. Putting things together, for positive c, today a mathematician is likely to write Bernoulli's formula as:
In fact this formula imperatively suggests to set B1 = ½ when switching from the so-called 'archaic' enumeration which uses only the even indices 2, 4, … to the modern form (more on different conventions in the next paragraph). Most striking in this context is the fact that the falling factorial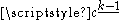
has for k = 0 the value 
.
Thus Bernoulli's formula can and has to be written:
If B1 stands for the value Bernoulli himself has given to the coefficient at that position.
Generalized Bernoulli numbers
The generalized Bernoulli numbers are certain algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s, defined similarly to the Bernoulli numbers, that are related to special valuesSpecial values of L-functionsIn mathematics, the study of special values of L-functions is a subfield of number theory devoted to generalising formulae such as the Leibniz formula for pi, namely...
of Dirichlet L-functions in the same way that Bernoulli numbers are related to special values of the Riemann zeta function.
Let χ be a primitive Dirichlet character modulo f. The generalized Bernoulli numbers attached to χ are defined by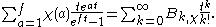
Let ε ∈ {0, 1} be defined by χ(−1) = (−1)ε. Then,- Bk,χ ≠ 0 if, and only if, .
Generalizing the relation between Bernoulli numbers and values of the Riemann zeta function at non-positive integers, one has the for all integers k ≥ 1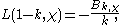
where L(s, χ) is the Dirichlet L-function of χ.
Assorted identities
A compact form of Bernoulli's formula makes use of an abstract symbol B:
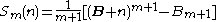
where the symbol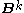
that appears during binomial expansion of the parenthesized term is to be replaced by the Bernoulli number 
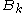(and 
). More suggestively and mnemonically, this may be written as a definite integral:
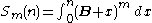
Many other Bernoulli identities can be written compactly with this symbol, e.g.
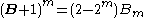
Let n be non-negative and even
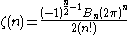
The nth cumulantCumulantIn probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
of the uniformUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on the interval [−1, 0] is Bn/n.
Let n¡ = 1/n! and n ≥ 1.
Then Bn is the following determinant:
Bn =
1
───
n¡
2¡
1¡
0
0
0
...
0
3¡
2¡
1¡
0
0
...
0
4¡
3¡
2¡
1¡
0
...
0
...
...
...
...
...
...
...
(n − 1)¡
...
...
3¡
2¡
1¡
0
n¡
(n − 1)¡
...
...
3¡
2¡
1¡
(n + 1)¡
n¡
(n − 1)¡
...
...
3¡
2¡
Thus the determinant is σn(1), the Stirling polynomial at x = 1.
For even-numbered Bernoulli numbers, B2p is given by the p X p determinant:
B2p =
(−1)p+1
───
(22p − 2)(2p)¡
3¡
1¡
0
0
0
...
0
5¡
3¡
1¡
0
0
...
0
7¡
5¡
3¡
1¡
0
...
0
...
...
...
...
...
...
...
(2p − 3)¡
...
...
5¡
3¡
1¡
0
(2p − 1)¡
(2p − 3)¡
...
...
5¡
3¡
1¡
(2p + 1)¡
(2p − 1)¡
(2p − 3)¡
...
...
5¡
3¡
Let n ≥ 1.
-
Let n ≥ 1. Then
-
Let n ≥ 0. Then (Leopold KroneckerLeopold KroneckerLeopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
1883)
-
Let n ≥ 1 and m ≥ 1. Then
-
Let n ≥ 4 and
the harmonic number. Then
-
Let n ≥ 4. Yuri Matiyasevich found (1997)
-
Let n ≥ 1
-
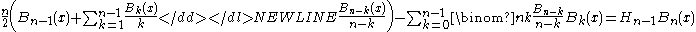
This is an identity by Faber-Pandharipande-Zagier-Gessel. Choose x = 0 or x = 1 to get a Bernoulli number identity according to your favourite convention.
-
The next formula is true for n ≥ 0 if B1 = B1(1) = 1/2, but only for n ≥ 1 if B1 = B1(0) = −1/2.
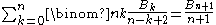
Let n ≥ 0 and [b] = 1 if b is true, 0 otherwise.
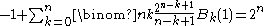
and
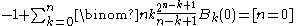
Values of the Bernoulli numbers
Bn = 0 for all odd n other than 1. B1 = 1/2 or −1/2 depending on the convention adopted (see above). The first few non-zero Bernoulli numbers (sequences and in OEIS) are listed below.
n
Numerator
Denominator
Decimal approximation (N/D)
0
1
1
+1.00000000000
1
-1
2
-0.50000000000
2
1
6
+0.16666666667
4
-1
30
-0.03333333333
6
1
42
+0.02380952381
8
-1
30
-0.03333333333
10
5
66
+0.07575757576
12
-691
2730
-0.25311355311
14
7
6
+1.16666666667
16
−3617
510
−7.09215686275
18
43867
798
+54.9711779448
See also
- Kummer's congruences
- poly-Bernoulli number
- q-Bernoulli number
- Bernoulli polynomialsBernoulli polynomialsIn mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
- Riemann zeta function
- Hurwitz zeta function
- Euler number
- Euler summationEuler summationEuler summation is a summability method for convergent and divergent series. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series....
External links
- The first 498 Bernoulli Numbers from Project GutenbergProject GutenbergProject Gutenberg is a volunteer effort to digitize and archive cultural works, to "encourage the creation and distribution of eBooks". Founded in 1971 by Michael S. Hart, it is the oldest digital library. Most of the items in its collection are the full texts of public domain books...
- The first 10,000 Bernoulli numbers
- A multimodular algorithm for computing Bernoulli numbers
- The Bernoulli Number Page
- Bernoulli number programs at LiteratePrograms
- The Computation of Irregular Primes
- Bernoullinumbers in context of Pascal-(Binomial)matrix german version
- summing of like powers in context with Pascal-/Bernoulli-matrix
- Some special properties, sums of Bernoulli-and related numbers
The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.
-
-
-
-
