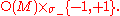Orientability
Encyclopedia


Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, orientability is a property of surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
measuring whether or not it is possible to make a consistent choice of surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
vector at every point. A choice of surface normal allows one to use the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
to define a "clockwise" direction of loops in the surface, as needed by Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
for instance. More generally, orientability of an abstract surface, or manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, measures whether one can consistently choose a "clockwise" orientation for all loops in the manifold. Equivalently, a surface is orientable if a two-dimensional figure such as
 in the space cannot be moved (continuously) around the space and back to where it started so that it looks like its own mirror image
in the space cannot be moved (continuously) around the space and back to where it started so that it looks like its own mirror image  .
.The notion of orientability can be generalized to higher dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s as well. A manifold is orientable if it has a consistent choice of orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, and a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
orientable manifold has exactly two different possible orientations. In this setting, various equivalent formulations of orientability can be given, depending on the desired application and level of generality. Formulations applicable to general topological manifolds often employ methods of homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
, whereas for differentiable manifolds more structure is present, allowing a formulation in terms of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s. An important generalization of the notion of orientability of a space is that of orientability of a family of spaces parameterized by some other space (a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
) for which an orientation must be selected in each of the spaces which varies continuously with respect to changes in the parameter values.
Orientable surfaces
A surface S in the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3 is orientable if a two-dimensional figure (for example,
 ) cannot be moved around the surface and back to where it started so that it looks like its own mirror image (
) cannot be moved around the surface and back to where it started so that it looks like its own mirror image ( ). Otherwise the surface is non-orientable. An abstract surface (i.e., a two-dimensional manifold
). Otherwise the surface is non-orientable. An abstract surface (i.e., a two-dimensional manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
) is orientable if a consistent concept of clockwise rotation can be defined on the surface in a continuous manner. That is to say that a loop going around one way on the surface can never be continuously deformed (without overlapping itself) to a loop going around the opposite way. This turns out to be equivalent to the question of whether the surface contains no subset that is homeomorphic to the Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
. Thus, for surfaces, the Möbius strip may be considered the source of all non-orientability.
For an orientable surface, a consistent choice of "clockwise" (as opposed to counter-clockwise) is called an orientation, and the surface is called oriented. For surfaces embedded in Euclidean space, an orientation is specified by the choice of a continuously varying surface normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
n at every point. If such a normal exists at all, then there are always two ways to select it: n or −n. More generally, an orientable surface admits exactly two orientations, and the distinction between an oriented surface and an orientable surface is subtle and frequently blurred. An orientable surface is an abstract surface that admits an orientation, while an oriented surface is a surface that is abstractly orientable, and has the additional datum of a choice of one of the two possible orientations.
Examples
Most surfaces we encounter in the physical world are orientable. Sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s, planes
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
, and tori
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
are orientable, for example. But Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
s, real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
s, and Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
s are non-orientable. They, as visualized in 3-dimensions, all have just one side. The real projective plane and Klein bottle cannot be embedded in R3, only immersed with nice intersections.
Note that locally an embedded surface always has two sides, so a near-sighted ant crawling on a one-sided surface would think there is an "other side". The essence of one-sidedness is that the ant can crawl from one side of the surface to the "other" without going through the surface or flipping over an edge, but simply by crawling far enough.
In general, the property of being orientable is not equivalent to being two-sided; however, this holds when the ambient space (such as R3 above) is orientable. For example, a torus embedded in

can be one-sided, and a Klein bottle in the same space can be two-sided; here
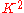 refers to the Klein bottle.
refers to the Klein bottle.Orientation by triangulation
Any surface has a triangulation
Triangulation (topology)
In mathematics, topology generalizes the notion of triangulation in a natural way as follows:A triangulation of a topological space X is a simplicial complex K, homeomorphic to X, together with a homeomorphism h:K\to X....
: a decomposition into triangles such that each edge on a triangle is glued to at most one other edge. Each triangle is oriented by choosing a direction around the perimeter of the triangle, associating a direction to each edge of the triangle. If this is done in such a way that, when glued together, neighboring edges are pointing in the opposite direction, then this determines an orientation of the surface. Such a choice is only possible if the surface is orientable, and in this case there are exactly two different orientations.
If the figure
 can be consistently positioned at all points of the surface without turning into its mirror image, then this will induce an orientation in the above sense on each of the triangles of the triangulation by selecting the direction of each of the triangles based on the order red-green-blue of colors of any of the figures in the interior of the triangle.
can be consistently positioned at all points of the surface without turning into its mirror image, then this will induce an orientation in the above sense on each of the triangles of the triangulation by selecting the direction of each of the triangles based on the order red-green-blue of colors of any of the figures in the interior of the triangle.This approach generalizes to any n-manifold having a triangulation. However, some 4-manifolds do not have a triangulation, and in general for n > 4 some n-manifolds have triangulations that are inequivalent.
Topological definitions
An n-dimensional manifold (either embedded in a finite dimensional vector space, or an abstract manifold) is called non-orientable if it is possible to take the homeomorphic image of an n-dimensional ball in the manifold and move it through the manifold and back to itself, so that at the end of the path, the ball has been reflected, using the same definition as for surfaces above. Equivalently, a n-dimensional manifold is non-orientable if it contains a homeomorphic image of the space formed by taking the direct product of a (n-1)-dimensional ball B and the unit interval [0,1] and gluing the ball B×{0} at one end to the ball B×{1} at other end with a single reflection. For surfaces, this space is a Möbius strip; for 3-manifold3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s, this is a solid Klein bottle
Solid Klein bottle
In mathematics, a solid Klein bottle is a 3-manifold homeomorphic to the quotient space obtained by gluing the top of \scriptstyle D^2 \times I to the bottom by a reflection, i.e...
.
As another alternative definition, in the language of structure groups, an orientable manifold is one whose structure group (a priori GL(n)) can be reduced to the subgroup GL+(n) of orientation-preserving transforms. Concretely, an orientable manifold is one that has a cover of open n-dimensional balls with consistent orientations (i.e. all transition maps are orientation preserving). Here one needs to define what a local orientation means, which can be done using orientations of vector bundles (a local orientation is an orientation of the tangent spaces at a point) or using singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
(an orientation is a choice of generator of the n-th relative homology
Relative homology
In algebraic topology, a branch of mathematics, the homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways...
group
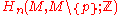
at a point p). A manifold is then said to be orientable if one can choose local orientations consistently throughout the manifold.
Using homology allows one to define orientability for compact n-manifolds without considering local orientations. A compact n-manifold M is orientable if and only if the top homology group,
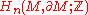 , is isomorphic to
, is isomorphic to  .
.Considering simplicial homology, which applies to any triangulable manifold, allows one to consider this a concrete statement about coherently orienting top-dimensional simplices in a triangulation, as done in the surface case above.
If the manifold has a differentiable structure, one can use the language of differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s (see below).
Orientation of differential manifolds
Another way of thinking about orientability is thinking of it as a choice of "right handedness" vs. "left handedness" at each point in the manifold. A differentiable manifold is said to be orientable if it is possible to select coordinate transitions so that there is a consistent choice of "right-hand" in each coordinate patch. More precisely, the manifold has a coordinate atlas all of whose transition functions have positive Jacobian determinants. A maximal such atlas gives an orientation on the manifold, and the manifold so equipped is then called oriented.Equivalently, a n-dimensional differentiable manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is orientable if there is a consistent choice of oriented basis of tangent vectors
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
at every point of the manifold. This can be formalized in a variety of ways, one of which is the condition that M should possess a volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
: a differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
ω of degree n which is nonzero at every point on the manifold. Given such an n-form, the atlas consisting of local diffeomorphisms sending ω to a positive multiple of the Euclidean volume form on Rn is oriented.
Orientable double cover
A closely related notion uses the idea of covering space. For a connected manifold M take M*, the set of pairs (x, o) where x is a point of M and o is an orientation at x; here we assume M is either smooth so we can choose an orientation on the tangent space at a point or we use singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
to define orientation. Then for every open, oriented subset of M we consider the corresponding set of pairs and define that to be an open set of M*. This gives M* a topology and the projection sending (x, o) to x is then a 2-1 covering map. This covering space is called the orientable double cover, as it is orientable. M* is connected if and only if M is not orientable.
Another way to construct this cover is to divide the loops based at a basepoint into either orientation-preserving or orientation-reversing loops. The orientation preserving loops generate a subgroup of the fundamental group which is either the whole group or of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
two. In the latter case (which means there is an orientation-reversing path), the subgroup corresponds to a connected double covering; this cover is orientable by construction. In the former case, one can simply take two copies of M, each of which corresponds to a different orientation.
Orientation of vector bundles
A real vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, which a priori has a GL(n) structure group, is called orientable when the structure group may be reduced
Reduction of the structure group
In mathematics, in particular the theory of principal bundles, one can ask if a G-bundle "comes from" a subgroup H In mathematics, in particular the theory of principal bundles, one can ask if a...
to
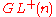 , the group of matrices
, the group of matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with positive determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. For the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, this reduction is always possible if the underlying base manifold is orientable and in fact this provides a convenient way to define the orientability of a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
real manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
: a smooth manifold is defined to be orientable if its tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
is orientable (as a vector bundle). Note that as a manifold in its own right, the tangent bundle is always orientable, even over nonorientable manifolds.
Linear algebra
The notion of orientability is essentially derived from the topology of the real general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
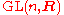 , specifically that the lowest homotopy group
, specifically that the lowest homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
is

an invertible transform of a real vector space is either orientation-preserving or orientation-reversing.
This holds not only for differentiable manifolds but for topological manifolds, as the space of self-homotopy equivalences of a sphere also has two connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
s, which can be denoted the "orientation-preserving" and "orientation-reversing" maps.
The analogous notion for the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
is the alternating group of even permutations
Even and odd permutations
In mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
.
Lorentzian geometry
In Lorentzian geometry, there are two kinds of orientability: space orientability and time orientability. These play a role in the causal structureCausal structure
In mathematical physics, the causal structure of a Lorentzian manifold describes the causal relationships between points in the manifold.- Introduction :In modern physics spacetime is represented by a Lorentzian manifold...
of spacetime. In the context of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a space-time manifold is space orientable if, whenever two right-handed observers head off in rocket ships starting at the same space-time point, and then meet again at another point, they remain right-handed with respect to one another. If a space-time is time-orientable then the two observers will always agree on the direction of time at both points of their meeting. In fact, a space-time is time-orientable if and only if any two observers can agree which of the two meetings preceded the other.
Formally, the pseudo-orthogonal group O(p,q) has a pair of characters
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
: the space orientation character σ+ and the time orientation character σ−,
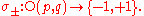
Their product σ = σ+σ− is the determinant, which gives the orientation character. A space-orientation of a pseudo-Riemannian manifold is identified with a section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the associated bundle
Associated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...

where O(M) is the bundle of pseudo-orthogonal frames. Similarly, a time orientation is a section of the associated bundle