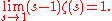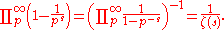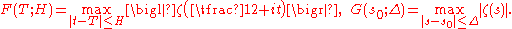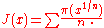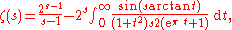Riemann zeta function
Encyclopedia
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of a complex variable s that analytically continues
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
the sum of the infinite series
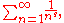 which converges when the real part of s is greater than 1. More general representations of ζ(s) for all s are given below. The Riemann zeta function plays a pivotal role in analytic number theory
which converges when the real part of s is greater than 1. More general representations of ζ(s) for all s are given below. The Riemann zeta function plays a pivotal role in analytic number theoryAnalytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
and has applications in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, and applied statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
.
First results about this function were obtained by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
in the eighteenth century. It is named after Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
, who in the memoir "On the Number of Primes Less Than a Given Magnitude
On the Number of Primes Less Than a Given Magnitude
die Anzahl der Primzahlen unter einer gegebenen is a seminal 8-page paper by Bernhard Riemann published in the November 1859 edition of the Monatsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin.Although it is the only paper he ever published on number theory, it...
", published in 1859, established a relation between its zeros and the distribution of prime numbers
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
.
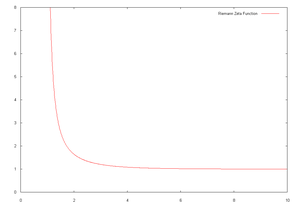
The values of the Riemann zeta function at even positive integers were computed by Euler. The first of them, ζ(2), provides a solution to the Basel problem
Basel problem
The Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate...
. In 1979 Apéry proved the irrationality of ζ(3). The values at negative integer points, also found by Euler, are rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s and play an important role in the theory of modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s. Many generalizations of the Riemann zeta function, such as Dirichlet series, Dirichlet L-functions and L-function
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
s, are known.
Definition
The Riemann zeta function ζ(s) is a function of a complex variable s = σ + it (here, s, σ and t are traditional notations associated to the study of the ζ-function). The following infinite series converges for all complex numbers s with real part greater than 1, and defines ζ(s) in this case: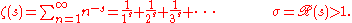
The Riemann zeta function is defined as the analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of the function defined for σ > 1 by the sum of the preceding series.
Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
considered the above series in 1740 for positive integer values of s, and later Chebyshev extended the definition to real s > 1.
The above series is a prototypical Dirichlet series that converges absolutely
Absolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
to an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
for s such that and diverges
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
for all other values of s. Riemann showed that the function defined by the series on the half-plane of convergence can be continued analytically
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to all complex values . For s = 1 the series is the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
which diverges to +∞
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
, and
Thus the Riemann zeta function is a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
on the whole complex s-plane, which is holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
everywhere except for a simple pole at s = 1 with residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
1.
Specific values
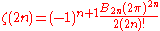
where B2n is a Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
; for negative integers, one has
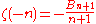
for , so in particular ζ vanishes at the negative even integers because Bm = 0 for all odd m other than 1. No such simple expression is known for odd positive integers.
The values of the zeta function obtained from integral arguments are called zeta constant
Zeta constant
In mathematics, a zeta constant is a number obtained by plugging an integer into the Riemann zeta function. This article provides a number of series identities for the zeta function for integer values.-The Riemann zeta function at 0 and 1:...
s. The following are the most commonly used values of the Riemann zeta function.
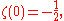

-
- this is the harmonic seriesHarmonic series (mathematics)In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
.
- this is the harmonic series

-
- this is employed in calculating the critical temperature for a Bose–Einstein condensateBose–Einstein condensateA Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
in a box with periodic boundary conditions, and for spin waveSpin waveSpin waves are propagating disturbances in the ordering of magnetic materials. These low-lying collective excitations occur in magnetic lattices with continuous symmetry. From the equivalent quasiparticle point of view, spin waves are known as magnons, which are boson modes of the spin lattice...
physics in magnetic systems.
- this is employed in calculating the critical temperature for a Bose–Einstein condensate

-
- the demonstration of this equality is known as the Basel problemBasel problemThe Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate...
. The reciprocal of this sum answers the question: What is the probability that two numbers selected at random are relatively primeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
?
- the demonstration of this equality is known as the Basel problem
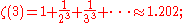
-
- this is called Apéry's constantApéry's constantIn mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
.
- this is called Apéry's constant

-
- Stefan–Boltzmann law and Wien approximation in physics.
Euler product formula
The connection between the zeta function and prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s was discovered by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, who proved the identity
Proof of the Euler product formula for the Riemann zeta function
Leonhard Euler proved the Euler product formula for the Riemann zeta function in his thesis Variae observationes circa series infinitas' ', published by St Petersburg Academy in 1737.-The Euler product formula:...
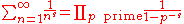
where, by definition, the left hand side is ζ(s) and the infinite product on the right hand side extends over all prime numbers p (such expressions are called Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
s):
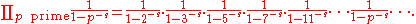
Both sides of the Euler product formula converge for Re(s) > 1. The proof of Euler's identity
Proof of the Euler product formula for the Riemann zeta function
Leonhard Euler proved the Euler product formula for the Riemann zeta function in his thesis Variae observationes circa series infinitas' ', published by St Petersburg Academy in 1737.-The Euler product formula:...
uses only the formula for the geometric series and the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. Since the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
, obtained when s = 1, diverges, Euler's formula (which becomes
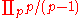 ) implies that there are infinitely many primes
) implies that there are infinitely many primesEuclid's theorem
Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. There are several well-known proofs of the theorem.-Euclid's proof:...
.
The Euler product formula can be used to calculate the asymptotic probability that s randomly selected integers are set-wise coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. Intuitively, the probability that any single number is divisible by a prime (or any integer), p is 1/p. Hence the probability that s numbers are all divisible by this prime is 1/ps, and the probability that at least one of them is not is . Now, for distinct primes, these divisibility events are mutually independent because the candidate divisors are coprime (a number is divisible by coprime divisors n and m if and only if it is divisible by nm, an event which occurs with probability 1/(nm).) Thus the asymptotic probability that s numbers are coprime is given by a product over all primes,
(More work is required to derive this result formally.)
The functional equation
The Riemann zeta function satisfies the functional equationFunctional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...

where Γ(s) is the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, which is an equality of meromorphic functions valid on the whole complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. This equation relates values of the Riemann zeta function at the points s and . The functional equation (owing to the properties of sin) implies that ζ(s) has a simple zero at each even negative integer s = − 2n — these are the trivial zeros of ζ(s).For s an even positive integer, the product sin(πs/2)Γ(1−s) is regular and the functional equation relates the values of the Riemann zeta function at odd negative integers and even positive integers.
The functional equation was established by Riemann in his 1859 paper On the Number of Primes Less Than a Given Magnitude
On the Number of Primes Less Than a Given Magnitude
die Anzahl der Primzahlen unter einer gegebenen is a seminal 8-page paper by Bernhard Riemann published in the November 1859 edition of the Monatsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin.Although it is the only paper he ever published on number theory, it...
and used to construct the analytic continuation in the first place. An equivalent relationship had been conjectured by Euler over a hundred years earlier, in 1749, for the Dirichlet eta function (alternating zeta function)
-

Incidentally, this relation is interesting also because it actually exhibits ζ(s) as a Dirichlet series (of the η-function) which is convergent (albeit non-absolutely) in the larger half-plane σ > 0 (not just σ > 1), up to an elementary factor.
Riemann also found a symmetric version of the functional equation, given by first defining
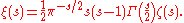
The functional equation is then given by
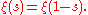
(Riemann defined a similar but different function which he called ξ(t).)
Zeros, the critical line, and the Riemann hypothesis
The functional equation shows that the Riemann zeta function has zeros at .. . These are called the trivial zeros. They are trivial in the sense that their existence is relatively easy to prove, for example, from sin(πs/2) being 0 in the functional equation. The non-trivial zeros have captured far more attention because their distribution not only is far less understood but, more importantly, their study yields impressive results concerning prime numbers and related objects in number theory. It is known that any non-trivial zero lies in the open strip {s ∈ C: 0 < Re(s) < 1}, which is called the critical strip. The Riemann hypothesis Riemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
Riemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
, considered one of the greatest unsolved problems in mathematics, asserts that any non-trivial zero s has Re(s) = 1/2. In the theory of the Riemann zeta function, the set {s ∈ C: Re(s) = 1/2} is called the critical line. For the Riemann zeta function on the critical line, see Z-functionZ functionIn mathematics, the Z-function is a function used for studying theRiemann zeta-function along the critical line where the real part of theargument is one-half.It is also called the Riemann-Siegel Z-function,the Riemann-Siegel zeta-function,...
.
The Hardy–Littlewood conjectures
In 1914 Godfrey Harold HardyG. H. HardyGodfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
proved that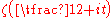 has infinitely many real zeros.
has infinitely many real zeros.
Let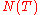 be the total number of real zeros,
be the total number of real zeros, 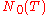 be the total number of zeros of odd order of the function
be the total number of zeros of odd order of the function 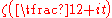 , lying on the interval
, lying on the interval
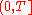 .
.
The next two conjectures of HardyG. H. HardyGodfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and John Edensor LittlewoodJohn Edensor LittlewoodJohn Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
on the distance between real zeros of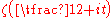 and on the density of zeros of
and on the density of zeros of 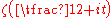 on the intervals
on the intervals  for sufficiently great
for sufficiently great  ,
, 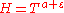 and with as less as possible value of
and with as less as possible value of  , where
, where  is an arbitrarily small number, open two new directions in the investigation of the Riemann zeta function:
is an arbitrarily small number, open two new directions in the investigation of the Riemann zeta function:
1. for any there exists such
there exists such 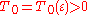 that for
that for  and
and  the interval
the interval  contains a zero of odd order of the function
contains a zero of odd order of the function 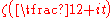 .
.
2. for any there exist
there exist 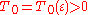 and
and 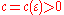 , such that for
, such that for  and
and 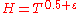 the inequality
the inequality 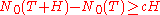 is true.
is true.
The Selberg conjecture
In 1942 Atle SelbergAtle SelbergAtle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
investigated the problem of Hardy–Littlewood 2 and proved that for any there exists such
there exists such 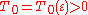 and
and 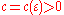 , such that for
, such that for  and
and  the inequality
the inequality  is true.
is true.
In his turn, SelbergAtle SelbergAtle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
claim a conjecture that it's possible to decrease the value of the exponent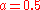 for
for 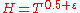 .
.
In 1984 Anatolii Alexeevitch KaratsubaAnatolii Alexeevitch KaratsubaAnatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...
proved that for a fixed satisfying the condition
satisfying the condition
 , a sufficiently large
, a sufficiently large  and
and 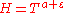 ,
, 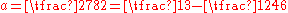 , the interval
, the interval  contains at least
contains at least 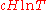 real zeros of the Riemann zeta function
real zeros of the Riemann zeta function 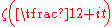 and therefore confirmed the Selberg conjecture.
and therefore confirmed the Selberg conjecture.
The estimates of Atle Selberg and Karatsuba can not be improved in respect of the order of growth as .
.
In 1992 A.A. KaratsubaAnatolii Alexeevitch KaratsubaAnatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...
proved, that an analog of the Selberg conjecture holds for «almost all» intervals ,
, 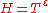 , where
, where  is an arbitrarily small fixed positive number. The Karatsuba method permits to investigate zeros of the Riemann zeta-function on «supershort» intervals of the critical line, that is, on the intervals
is an arbitrarily small fixed positive number. The Karatsuba method permits to investigate zeros of the Riemann zeta-function on «supershort» intervals of the critical line, that is, on the intervals  , the length
, the length  of which grows slower than any, even arbitrarily small degree
of which grows slower than any, even arbitrarily small degree  . In particular, he proved that for any given numbers
. In particular, he proved that for any given numbers  ,
,  satisfying the conditions
satisfying the conditions 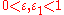 almost all intervals
almost all intervals  for
for  contain at least
contain at least 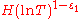 zeros of the function
zeros of the function 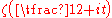 . This estimate is quite close to the one that follows from the Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. This estimate is quite close to the one that follows from the Riemann hypothesisRiemann hypothesisIn mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.
Other results
The location of the Riemann zeta function's zeros is of great importance in the theory of numbers. From the fact that all non-trivial zeros lie in the critical strip one can deduce the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. A better result is that ≠ 0 whenever |t| ≥ 3 and

The strongest result of this kind one can hope for is the truth of the Riemann hypothesis, which would have many profound consequences in the theory of numbers.
It is known that there are infinitely many zeros on the critical line. LittlewoodJohn Edensor LittlewoodJohn Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
showed that if the sequence (γn) contains the imaginary parts of all zeros in the upper half-plane in ascending order, then
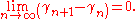
The critical line theorem asserts that a positive percentage of the nontrivial zeros lies on the critical line.
In the critical strip, the zero with smallest non-negative imaginary part is ... Directly from the functional equation one sees that the non-trivial zeros are symmetric about the axis Re(s) = 1/2. Furthermore, the fact that ζ(s) = ζ(s*)* for all complex (* indicating complex conjugation) implies that the zeros of the Riemann zeta function are symmetric about the real axis.
The statistics of the Riemann zeta zeros are a topic of interest to mathematicians because of their connection to big problems like the Riemann hypothesis, distribution of prime numbers, etc. Through connections with random matrixRandom matrixIn probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
theory and quantum chaosQuantum chaosQuantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
, the appeal is even broader. The fractal structure of the Riemann zeta zero distribution has been studied using rescaled range analysis. The self-similarity of the zero distribution is quite remarkable, and is characterized by a large fractal dimensionFractal dimensionIn fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
of 1.9. This rather large fractal dimension is found over zeros covering at least fifteen orders of magnitude, and also for the zeros of other L-functionL-functionThe theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
s.
Various properties
For sums involving the zeta-function at integer and half-integer values, see rational zeta seriesRational zeta seriesIn mathematics, a rational zeta series is the representation of an arbitrary real number in terms of a series consisting of rational numbers and the Riemann zeta function or the Hurwitz zeta function...
.
Reciprocal
The reciprocal of the zeta function may be expressed as a Dirichlet series over the Möbius functionMöbius functionThe classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
μ(n):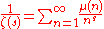
for every complex number s with real part > 1. There are a number of similar relations involving various well-known multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
s; these are given in the article on the Dirichlet series.
The Riemann hypothesis is equivalent to the claim that this expression is valid when the real part of s is greater than 1/2.
Universality
The critical strip of the Riemann zeta function has the remarkable property of universality. This zeta-function universalityZeta function universalityIn mathematics, the universality of zeta-functions is the remarkable ability of the Riemann zeta-function and other, similar, functions, such as the Dirichlet L-functions, to approximate arbitrary non-vanishing holomorphic functions arbitrarily well....
states that there exists some location on the critical strip that approximates any holomorphic function arbitrarily well. Since holomorphic functions are very general, this property is quite remarkable.
Estimates of the maximum of the modulus of the zeta function
Let the functions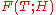 and
and 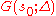 be defined by the equalities
be defined by the equalities
Here is a sufficiently large positive number,
is a sufficiently large positive number,  ,
, 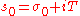 ,
, 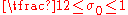 ,
,  . Estimating the values
. Estimating the values  and
and  from below shows, how large (in modulus) values
from below shows, how large (in modulus) values 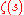 can take on short intervals of the critical line or in small neighborhoods of points lying in the critical strip
can take on short intervals of the critical line or in small neighborhoods of points lying in the critical strip  .
.
The case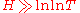 was studied by Ramachandra; the case
was studied by Ramachandra; the case  , where
, where  is a sufficiently large constant, is trivial.
is a sufficiently large constant, is trivial.
KaratsubaAnatolii Alexeevitch KaratsubaAnatolii Alexeevitch Karatsuba was a Russian mathematician, who authored the first fast multiplication method: the Karatsuba algorithm, a fast procedure for multiplying large numbers.- Studies and work :...
proved, in particular, that if the values and
and  exceed certain sufficiently small constants, then the estimates
exceed certain sufficiently small constants, then the estimates

hold, where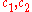 are certain absolute constants.
are certain absolute constants.
The argument of the Riemann zeta-function
The function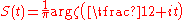 is called the argument of the Riemann zeta function.
is called the argument of the Riemann zeta function.
Here is the increment of an arbitrary continuous branch of
is the increment of an arbitrary continuous branch of 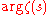 along the broken line joining the points
along the broken line joining the points  and
and 
There are some theorems on properties of the function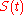 . Among those results are the mean value theorems for
. Among those results are the mean value theorems for  and its first integral
and its first integral 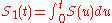 on intervals of the real line, and also the theorem claiming that every interval
on intervals of the real line, and also the theorem claiming that every interval  for
for 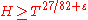 contains at least
contains at least
points where the function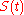 changes sign. Earlier similar results were obtained by Atle SelbergAtle SelbergAtle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
changes sign. Earlier similar results were obtained by Atle SelbergAtle SelbergAtle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
for the case
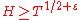 .
.
Mellin transform
The Mellin transformMellin transformIn mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
of a function ƒ(x) is defined as
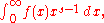
in the region where the integral is defined. There are various expressions for the zeta-function as a Mellin transform. If the real part of s is greater than one, we have
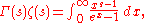
where Γ denotes the Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. By modifying the contour Riemann showed that
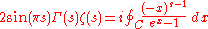
for all s, where the contour C starts and ends at +∞ and circles the origin once.
We can also find expressions which relate to prime numbers and the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. If π(x) is the prime-counting function, then

for values with .
A similar Mellin transform involves the Riemann prime-counting function J(x), which counts prime powers pn with a weight of 1/n, so that
Now we have
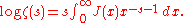
These expressions can be used to prove the prime number theorem by means of the inverse Mellin transform. Riemann's prime-counting function is easier to work with, and π(x) can be recovered from it by Möbius inversionMöbius inversion formulaIn mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
.
Theta functions
The Riemann zeta function can be given formally by a divergent Mellin transform
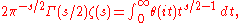
in terms of Jacobi's theta function

However this integral does not converge for any value of s and so needs to be regularized: this gives the following expression for the zeta function:
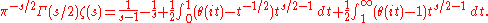
Laurent series
The Riemann zeta function is meromorphic with a single pole of order one at
s = 1. It can therefore be expanded as a Laurent seriesLaurent seriesIn mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
about s = 1;
the series development then is
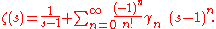
The constants γn here are called the Stieltjes constants and can be defined
by the limitLimit of a sequenceThe limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
-

The constant term γ0 is the Euler–Mascheroni constant.
Integral
For all the integral relation
the integral relation
holds true, which may be used for a numerical evaluation of the Zeta-function.
Rising factorial
Another series development using the rising factorialPochhammer symbolIn mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
valid for the entire complex plane is

This can be used recursively to extend the Dirichlet series definition to all complex numbers.
The Riemann zeta function also appears in a form similar to the Mellin transform in an integral over the Gauss–Kuzmin–Wirsing operator acting on xs−1; that context gives rise to a series expansion in terms of the falling factorial.
Hadamard product
On the basis of Weierstrass's factorization theoremWeierstrass factorization theoremIn mathematics, the Weierstrass factorization theorem in complex analysis, named after Karl Weierstrass, asserts that entire functions can be represented by a product involving their zeroes...
, Hadamard gave the infinite product expansion
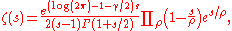
where the product is over the non-trivial zeros ρ of ζ and the letter γ again denotes the Euler–Mascheroni constantEuler–Mascheroni constantThe Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
. A simpler infinite product expansion is
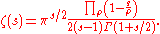
This form clearly displays the simple pole at s = 1, the trivial zeros at −2, −4, ... due to the gamma function term in the denominator, and the non-trivial zeros at s = ρ.
Logarithmic derivative on the critical strip
-

where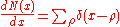 is the density of zeros of ζ on the critical strip 0 < Re(s) < 1 (δ is the Dirac delta distribution, and the sum is over the nontrivial zeros ρ of ζ).
is the density of zeros of ζ on the critical strip 0 < Re(s) < 1 (δ is the Dirac delta distribution, and the sum is over the nontrivial zeros ρ of ζ).
Globally convergent series
A globally convergent series for the zeta function, valid for all complex numbers s except for some integer n, was conjectured by Konrad KnoppKonrad KnoppHe also authored two texts on functions of a complex variable as well as a problem book:He also produced the sixth edition of the three-volume work :-References:...
and proved by Helmut HasseHelmut HasseHelmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
in 1930 (cf. Euler summationEuler summationEuler summation is a summability method for convergent and divergent series. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series....
):
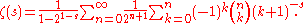
The series only appeared in an Appendix to Hasse's paper, and did not become generally known until it was rediscovered more than 60 years later (see Sondow, 1994).
Peter BorweinPeter BorweinPeter Benjamin Borwein is a Canadian mathematicianand a professor at Simon Fraser University. He is known as a co-discoverer of the Bailey-Borwein-Plouffe algorithm for computing π.-First interest in mathematics:...
has shown a very rapidly convergent series suitable for high precision numerical calculations. The algorithm, making use of Chebyshev polynomials, is described in the article on the Dirichlet eta function.
Applications
The zeta function occurs in applied statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
(see Zipf's law and Zipf–Mandelbrot law).
Zeta function regularizationZeta function regularizationIn mathematics and theoretical physics, zeta function regularization is a type of regularization or summability method that assigns finite values to divergent sums or products, and in particular can be used to define determinants and traces of some self-adjoint operators...
is used as one possible means of regularizationRegularization (physics)-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
of divergent seriesDivergent seriesIn mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
in quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. In one notable example, the Riemann
zeta-function shows up explicitly in the calculation of the Casimir effectCasimir effectIn quantum field theory, the Casimir effect and the Casimir–Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, like capacitors placed a few micrometers apart, without any external electromagnetic field...
. The zeta function is also useful for the analysis of dynamical systems, see .
Generalizations
There are a number of related zeta functions that can be considered to be generalizations of the Riemann zeta function. These include the Hurwitz zeta function

(the convergent series representation was given by Helmut HasseHelmut HasseHelmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
in 1930, cf. Hurwitz zeta function), which coincides with the Riemann zeta function when q = 1 (note that the lower limit of summation in the Hurwitz zeta function is 0, not 1), the Dirichlet L-functions and the Dedekind zeta-function. For other related functions see the articles Zeta function and L-functionL-functionThe theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
.
The polylogarithm is given by

which coincides with the Riemann zeta function when z = 1.
The Lerch transcendent is given by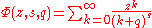
which coincides with the Riemann zeta function when z = 1 and q = 1 (note that the lower limit of summation in the Lerch transcendent is 0, not 1).
The Clausen function Cls(θ) that can be chosen as the real or imaginary part of Lis(e iθ).
The multiple zeta functions are defined by

One can analytically continue these functions to the n-dimensional complex space. The special values of these functions are called multiple zeta values by number theorists and have been connected to many different branches in mathematics and physics.
See also
- Generalized Riemann hypothesisGeneralized Riemann hypothesisThe Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global L-functions, which are formally similar to the Riemann zeta-function...
- Riemann–Siegel theta function
- Prime zeta function
- 1 + 2 + 3 + 4 + ···
External links
- Riemann Zeta Function, in Wolfram Mathworld — an explanation with a more mathematical approach
- Tables of selected zeros
- Prime Numbers Get Hitched A general, non-technical description of the significance of the zeta function in relation to prime numbers.
- X-Ray of the Zeta Function Visually oriented investigation of where zeta is real or purely imaginary.
- Formulas and identities for the Riemann Zeta function functions.wolfram.com
- Riemann Zeta Function and Other Sums of Reciprocal Powers, section 23.2 of Abramowitz and StegunAbramowitz and StegunAbramowitz and Stegun is the informal name of a mathematical reference work edited by Milton Abramowitz and Irene Stegun of the U.S. National Bureau of Standards...
- The Riemann Hypothesis - A Visual Exploration — a visual exploration of the Riemann Hypothesis and Zeta Function
- Generalized Riemann hypothesis
-
-