Inverse relation
Encyclopedia
In mathematics
, the inverse relation of a binary relation
is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'. In formal terms, if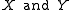
are sets and 
is a relation
from X to Y then
is the relation defined so that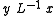 
if and only if 
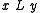(Halmos 1975, p. 40). In another way, 
.
The notation comes by analogy with that for an inverse function
. Though many functions do not have an inverse; every relation does.
The inverse relation is also called the converse relation or transpose relation (in view of its similarity with the transpose
of a matrix: these are the most familiar examples of dagger categories
), and may be written as LC, LT, L~ or
.
Note that, despite the notation, the converse relation is not an inverse in the sense of composition of relations
:
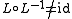in general.
(in the language of dagger categories
, it is self-adjoint).
If a relation is reflexive
, irreflexive, symmetric
, antisymmetric
, asymmetric
, transitive
, total
, trichotomous, a partial order, total order
, strict weak order, total preorder (weak order), or an equivalence relation
, its inverse is too.
However, if a relation is extendable, this need not be the case for the inverse.
The operation of taking a relation to its inverse gives the category of relations
Rel the structure of a dagger category
.
The the set of all binary relation
s B(X) on a set X is a semigroup with involution
with the involution being the mapping of a relation to its inverse relation.
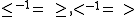, etc.
The inverse relation of a function
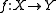is the relation 
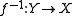defined by 
.
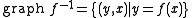This is not necessarily a function: One necessary condition is that f be injective, since else
is multi-valued. This condition is sufficient for 
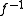being a partial function
, and it is clear that
then is a (total) function if and only if
f is surjective.
In that case, i.e. if f is bijective,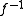
may be called the inverse function
of f.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the inverse relation of a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'. In formal terms, if
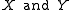are sets and is a relationfrom X to Y then
is the relation defined so that 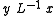if and only if 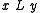(Halmos 1975, p. 40). In another way, .The notation comes by analogy with that for an inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
. Though many functions do not have an inverse; every relation does.
The inverse relation is also called the converse relation or transpose relation (in view of its similarity with the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of a matrix: these are the most familiar examples of dagger categories
Dagger category
In mathematics, a dagger category is a category equipped with a certain structure called dagger or involution...
), and may be written as LC, LT, L~ or
.Note that, despite the notation, the converse relation is not an inverse in the sense of composition of relations
Composition of relations
In mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
:
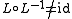in general.Properties
A relation equal to its inverse is a symmetric relationSymmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
(in the language of dagger categories
Dagger category
In mathematics, a dagger category is a category equipped with a certain structure called dagger or involution...
, it is self-adjoint).
If a relation is reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, irreflexive, symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
, antisymmetric
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
, asymmetric
Asymmetric relation
Asymmetric often means, simply: not symmetric. In this sense an asymmetric relation is a binary relation which is not a symmetric relation.That is,\lnot....
, transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, total
Total relation
In mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
, trichotomous, a partial order, total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
, strict weak order, total preorder (weak order), or an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, its inverse is too.
However, if a relation is extendable, this need not be the case for the inverse.
The operation of taking a relation to its inverse gives the category of relations
Category of relations
In mathematics, the category Rel has the class of sets as objects and binary relations as morphisms.A morphism R : A → B in this category is a relation between the sets A and B, so ....
Rel the structure of a dagger category
Dagger category
In mathematics, a dagger category is a category equipped with a certain structure called dagger or involution...
.
The the set of all binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s B(X) on a set X is a semigroup with involution
Semigroup with involution
In mathematics, in semigroup theory, an involution in a semigroup is a transformation of the semigroup which is its own inverse and which is an anti-automorphism of the semigroup. A semigroup in which an involution is defined is called a semigroup with involution...
with the involution being the mapping of a relation to its inverse relation.
Examples
For usual (maybe strict or partial) order relations, the converse is the naively expected "opposite" order, e.g.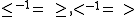, etc.Inverse relation of a function
A function is invertible if and only if its inverse relation is a function, in which case the inverse relation is the inverse function.The inverse relation of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
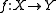is the relation 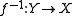defined by 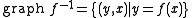.This is not necessarily a function: One necessary condition is that f be injective, since else
is multi-valued. This condition is sufficient for 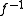being a partial functionPartial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
, and it is clear that
then is a (total) function if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
f is surjective.
In that case, i.e. if f is bijective,
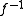may be called the inverse functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of f.
See also
- BijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
- Function (mathematics)Function (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
- Inverse functionInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
- Inverse relationshipInverse relationshipAn inverse or negative relationship is a mathematical relationship in which one variable, say y, decreases as another, say x, increases. For a linear relation, this can be expressed as y = a-bx, where -b is a constant value less than zero and a is a constant...
- Relation (mathematics)Relation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...