
P-adic number
Encyclopedia
In mathematics
, and chiefly number theory
, the p-adic number system for any prime number
p extends the ordinary arithmetic
of the rational numbers in a way different from the extension of the rational number system
to the real
and complex number
systems. The extension is achieved by an alternative interpretation of the concept of absolute value
.
First described by Kurt Hensel
in 1897, the p-adic numbers were motivated primarily by an attempt to bring the ideas and techniques of power series methods into number theory. Their influence now extends far beyond this. For example, the field of p-adic analysis
essentially provides an alternative form of calculus
.
More formally, for a given prime p, the field
Qp of p-adic numbers is a completion
of the rational number
s. The field Qp is also given a topology
derived from a metric
, which is itself derived from an alternative valuation
on the rational numbers. This metric space is complete in the sense that every Cauchy sequence
converges to a point in Qp. This is what allows the development of calculus on Qp, and it is the interaction of this analytic and algebraic structure which gives the p-adic number systems their power and utility.
The p in p-adic is a variable
and may be replaced with a constant
(yielding, for instance, "the 2-adic numbers") or another placeholder variable (for expressions such as "the ℓ-adic numbers").
In the standard decimal representation, almost all
real number
s do not have a terminating decimal representation. For example, 1/3 is represented as a non-terminating decimal as follows

Informally, non-terminating decimals are easily understood, because it is clear that a real number can be approximated to any required degree of precision
by a terminating decimal. If two decimal expansions differ only after the 10th decimal place, they are quite close to one another; and if they differ only after the 20th decimal place, they are even closer.
10-adic numbers use a similar non-terminating expansion, but with a different concept of "closeness" called a metric
. Whereas two decimal expansions are close to one another if they differ by a large negative power of 10, two 10-adic expansions are close if they differ by a large positive power of 10. Thus 3333 and 4333, which differ by 103, are close in the 10-adic metric, and 33333333 and 43333333 are even closer, differing by 107.
In the 10-adic metric, the following sequence of numbers gets closer and closer to −1:


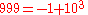
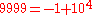
and taking this sequence to its limit, we can say (informally) that the 10-adic expansion of −1 is
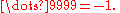
In this notation, 10-adic expansions can be extended indefinitely to the left, in contrast to decimal expansions, which can be extended indefinitely to the right. Note that this is not the only way to write p-adic numbers—for alternatives see the Notation section below.
More formally, a 10-adic number can be defined as

where each of the ai is a digit
taken from the set {0, 1, …..., 9} and the initial index n may be positive, negative or 0, but must be finite. From this definition, it is clear that positive integers and positive rational number
s with terminating decimal expansions will have terminating 10-adic expansions that are identical to their decimal expansions. Other numbers may have non-terminating 10-adic expansions.
It is possible to define addition, subtraction, and multiplication on 10-adic numbers in a consistent way, so that the 10-adic numbers form a commutative ring
.
We can create 10-adic expansions for negative numbers as follows
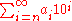

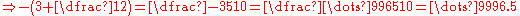
and fractions which have non-terminating decimal expansions also have non-terminating 10-adic expansions. For example
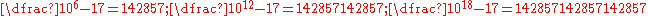

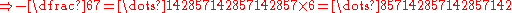

Generalizing the last example, we can find a 10-adic expansion for any rational number p⁄q such that q is co-prime to 10; Euler's theorem guarantees that if q is co-prime to 10, then there is an n such that 10n − 1 is a multiple of q.
However, 10-adic numbers have one major drawback. It is possible to find pairs of non-zero 10-adic numbers whose product is 0. In other words, the 10-adic numbers are not a domain because they contain zero divisor
s. This turns out to be because 10 is a composite number
which is not a power of a prime. This problem is avoided by using a prime number p as the base
of the number system instead of 10.
can be written in a base p expansion in the form
where the ai are integers in {0, …, p − 1}. For example, the binary
expansion of 35 is 1·25 + 0·24 + 0·23 + 0·22 + 1·21 + 1·20, often written in the shorthand notation 1000112.
The familiar approach to extending this description to the larger domain of the rationals (and, ultimately, to the reals) is to use sums of the form:

A definite meaning is given to these sums based on Cauchy sequence
s, using the absolute value
as metric. Thus, for example, 1/3 can be expressed in base 5 as the limit of the sequence 0.1313131313...5. In this formulation, the integers are precisely those numbers for which ai = 0 for all i < 0.
As an alternative, if we extend the base p expansions by allowing infinite sums of the form
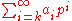
where k is some (not necessarily positive) integer, we obtain the p-adic expansions defining the field
Qp of p-adic numbers. Those p-adic numbers for which ai = 0 for all i < 0 are also called the p-adic integers. The p-adic integers form a subring
of Qp, denoted Zp. (Not to be confused with the ring of integers modulo p which is also sometimes written Zp. To avoid ambiguity, Z/pZ or Z/(p) are often used to represent the integers modulo p.)
Intuitively, as opposed to p-adic expansions which extend to the right as sums of ever smaller, increasingly negative powers of the base p (as is done for the real numbers as described above), these are numbers whose p-adic expansion to the left are allowed to go on forever. For example, the p-adic expansion of 1/3 in base 5 is …1313132, i.e. the limit of the sequence 2, 32, 132, 3132, 13132, 313132, 1313132,… . Multiplying this infinite sum by 3 in base 5 gives …0000001. As there are no negative powers of 5 in this expansion of 1/3 (i.e. no numbers to the right of the decimal point), we see that 1/3 is a p-adic integer in base 5.
While it is possible to use this approach to rigorously define p-adic numbers and explore their properties, just as in the case of real numbers other approaches are generally preferred. Hence we want to define a notion of infinite sum which makes these expressions meaningful, and this is most easily accomplished by the introduction of the p-adic metric. Two different but equivalent solutions to this problem are presented in the Constructions section below.
of p increase from right to left. With this right-to-left notation the 3-adic expansion of 1/5, for example, is written as
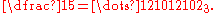
When performing arithmetic in this notation, digits are carried to the left. It is also possible to write p-adic expansions so that the powers of p increase from left to right, and digits are carried to the right. With this left-to-right notation the 3-adic expansion of 1/5 is
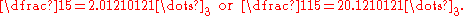
p-adic expansions may be written with other sets of digits instead of {0, 1, …, p − 1}. For example, the 3-adic expansion of 1/5 can be written using balanced ternary
digits {1,0,1} as

In fact any set of p integers which are in distinct residue classes modulo
p may be used as p-adic digits. In number theory, Teichmüller digits are sometimes used.
s can be defined as equivalence classes of Cauchy sequence
s of rational number
s; this allows us to, for example, write 1 as 1.000… = 0.999… . The definition of a Cauchy sequence relies on the metric
chosen, though, so if we choose a different one, we can construct numbers other than the real numbers. The usual metric which yields the real numbers is called the Euclidean metric.
For a given prime p, we define the p-adic absolute value in Q as follows:
for any non-zero rational number x, there is a unique integer n allowing us to write x = pn(a/b), where neither of the integers a and b is divisible
by p. Unless the numerator or denominator of x in lowest terms contains p as a factor, n will be 0. Now define |x|p = p−n. We also define |0|p = 0.
For example with x = 63/550 = 2−1 32 5−2 7 11−1
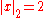


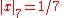


This definition of |x|p has the effect that high powers of p become "small".
By the fundamental theorem of arithmetic
, for a given non-zero rational number x there is a unique finite set of distinct primes and a corresponding sequence of non-zero integers
and a corresponding sequence of non-zero integers  such that:
such that: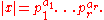
It then follows that for all
for all 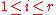 , and
, and 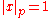 for any other prime
for any other prime 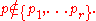
It is a theorem of Ostrowski
that each absolute value
on Q is equivalent either to the Euclidean absolute value, the trivial absolute value, or to one of the p-adic absolute values for some prime p. The p-adic absolute value defines a metric dp on Q by setting
The field Qp of p-adic numbers can then be defined as the completion of the metric space (Q,dp); its elements are equivalence classes of Cauchy sequences, where two sequences are called equivalent if their difference converges to zero. In this way, we obtain a complete metric space which is also a field and contains Q.
It can be shown that in Qp, every element x may be written in a unique way as
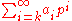
where k is some integer and each ai is in {0, …, p − 1}. This series converges
to x with respect to the metric dp.
With this absolute value, the field Qp is a local field
.
We start with the inverse limit
of the rings
Z/pnZ (see modular arithmetic
): a p-adic integer is then a sequence
(an)n≥1 such that an is in
Z/pnZ, and if n ≤ m, then
an ≡ am (mod pn).
Every natural number m defines such a sequence (an) by an = m mod pn and can therefore be regarded as a p-adic integer. For example, in this case 35 as a 2-adic integer would be written as the sequence (1, 3, 3, 3, 3, 35, 35, 35, …).
The operators of the ring amount to pointwise addition and multiplication of such sequences. This is well defined because addition and multiplication commute with the mod operator, see modular arithmetic.
Moreover, every sequence (an) where the first element is not 0 has an inverse. In that case, for every n, an and p are coprime
, and so an and pn are relatively prime. Therefore, each an has an inverse mod pn, and the sequence of these inverses, (bn), is the sought inverse of (an). For example, consider the p-adic integer corresponding to the natural number 7; as a 2-adic number, it would be written (1, 3, 7, 7, 7, 7, 7, ...). This object's inverse would be written as an ever-increasing sequence that begins (1, 3, 7, 7, 23, 55, 55, 183, 439, 439, 1463 ...). Naturally, this 2-adic integer has no corresponding natural number.
Every such sequence can alternatively be written as a series of the form we considered above. For instance, in the 3-adics, the sequence (2, 8, 8, 35, 35, ...) can be written as 2 + 2·3 + 0·32 + 1·33 + 0·34 + ... The partial sums of this latter series are the elements of the given sequence.
The ring of p-adic integers has no zero divisors, so we can take the field of fractions
to get the field Qp of p-adic numbers. Note that in this field of fractions, every non-integer p-adic number can be uniquely written as p−nu with a natural number
n and a unit in the p-adic integers u. This means that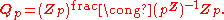
Note that , where
, where 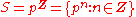 is a multiplicative subset (contains the unit and closed under multiplication) of a commutative ring with unit
is a multiplicative subset (contains the unit and closed under multiplication) of a commutative ring with unit  , is an algebraic construction called the ring of fractions of
, is an algebraic construction called the ring of fractions of  by
by  .
.
of the finite rings Z/pkZ, but is nonetheless uncountable
, and has the cardinality of the continuum
. Accordingly, the field Qp is uncountable. The endomorphism ring
of the Prüfer p-group
of rank n, denoted Z(p∞)n, is the ring of n×n matrices over the p-adic integers; this is sometimes referred to as the Tate module
.
The p-adic numbers contain the rational numbers Q and form a field of characteristic
0. This field cannot be turned into an ordered field
.
Let the topology τ on Zp be defined by taking as a basis all sets of the form Ua(n) = {n + λ pa for λ in Zp and a in N}. Then Zp is a compactification
of Z, under the derived topology (it is not a compactification of Z with its usual topology). The relative topology on Z as a subset of Zp is called the p-adic topology on Z.
The topology of the set of p-adic integers is that of a Cantor set
; the topology of the set of p-adic numbers is that of a Cantor set minus a point (which would naturally be called infinity). In particular, the space of p-adic integers is compact
while the space of p-adic numbers is not; it is only locally compact.
As metric space
s, both the p-adic integers and the p-adic numbers are complete.
The real numbers have only a single proper algebraic extension
, the complex number
s; in other words, this quadratic extension is already algebraically closed
. By contrast, the algebraic closure
of the p-adic numbers has infinite degree. Furthermore, Qp has infinitely many inequivalent algebraic extensions. Also contrasting the case of real numbers, the algebraic closure of Qp is not (metrically) complete. Its (metric) completion is called Cp. Here an end is reached, as Cp is algebraically closed.
The field Cp is isomorphic to the field C of complex numbers, so we may regard Cp as the complex numbers endowed with an exotic metric. It should be noted that the proof of existence of such a field isomorphism relies on the axiom of choice, and does not provide an explicit example of such an isomorphism.
The p-adic numbers contain the nth cyclotomic field
(n>2) if and only if n divides p − 1. For instance, the nth cyclotomic field is a subfield of Q13 if and only if n = 1, 2, 3, 4, 6, or 12. In particular, there is no multiplicative p-torsion in the p-adic numbers, if p > 2. Also, -1 is the only non-trivial torsion element in 2-adic numbers.
Given a natural number k, the index of the multiplicative group of the k-th powers of the non-zero elements of Qp in the multiplicative group of Qp is finite.
The number e
, defined as the sum of reciprocals of factorial
s, is not a member of any p-adic field; but ep is a p-adic number for all p except 2, for which one must take at least the fourth power. (Thus a number with similar properties as e - namely a pth root of ep - is a member of the algebraic closure of the p-adic numbers for all p.)
Over the reals, the only functions whose derivative
is zero are the constant functions. This is not true over Qp. For instance, the function
has zero derivative everywhere but is not even locally constant
at 0.
Given any elements r∞, r2, r3, r5, r7, ... where rp is in Qp (and Q∞ stands for R), it is possible to find a sequence (xn) in Q such that for all p (including ∞), the limit of xn in Qp is rp.
The field Qp is a locally compact Hausdorff space
.
If is a finite Galois extension
is a finite Galois extension
of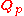 ,
,
the Galois group
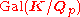 is solvable
is solvable
.
Thus, the Galois group is prosolvable.
is prosolvable.
, its reciprocal will require 2n−1 bits to represent.
s, in an analogous way. This will be described now.
Suppose D is a Dedekind domain
and E is its field of fractions
. Pick a non-zero prime ideal
P of D. If x is a non-zero element of E, then xD is a fractional ideal
and can be uniquely factored as a product of positive and negative powers of non-zero prime ideals of D. We write ordP(x) for the exponent of P in this factorization, and for any choice of number c greater than 1 we can set
Completing with respect to this absolute value |.|P yields a field EP, the proper generalization of the field of p-adic numbers to this setting.
The choice of c does not change the completion (different choices yield the same concept of Cauchy sequence, so the same completion).
It is convenient, when the residue field
D/P is finite, to take for c the size of D/P.
For example, when E is a number field, Ostrowski's theorem
says that every non-trivial non-Archimedean absolute value
on E arises as some |.|P. The remaining non-trivial absolute values
on E arise from the different embeddings of E into the real or complex numbers. (In fact, the non-Archimedean absolute values can be considered as simply the different embeddings of E into the fields Cp, thus putting the description of all
the non-trivial absolute values of a number field on a common footing.)
Often, one needs to simultaneously keep track of all the above mentioned completions when E is a number field (or more generally a global field
), which are seen as encoding "local" information. This is accomplished by adele ring
s and idele groups.
's local-global principle is said to hold for an equation if it can be solved over the rational numbers if and only if
it can be solved over the real number
s and over the p-adic numbers for every prime p.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and chiefly number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the p-adic number system for any prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p extends the ordinary arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
of the rational numbers in a way different from the extension of the rational number system
Number system
In mathematics, a 'number system' is a set of numbers, , together with one or more operations, such as addition or multiplication....
to the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
systems. The extension is achieved by an alternative interpretation of the concept of absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
.
First described by Kurt Hensel
Kurt Hensel
Kurt Wilhelm Sebastian Hensel was a German mathematician born in Königsberg, Prussia.He was the son of the landowner and entrepreneur Sebastian Hensel, brother of the philosopher Paul Hensel, grandson of the composer Fanny Mendelssohn and the painter Wilhelm Hensel, and a descendant of the...
in 1897, the p-adic numbers were motivated primarily by an attempt to bring the ideas and techniques of power series methods into number theory. Their influence now extends far beyond this. For example, the field of p-adic analysis
P-adic analysis
In mathematics, p-adic analysis is a branch of number theory that deals with the mathematical analysis of functions of p-adic numbers....
essentially provides an alternative form of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
.
More formally, for a given prime p, the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
Qp of p-adic numbers is a completion
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
of the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. The field Qp is also given a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
derived from a metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, which is itself derived from an alternative valuation
P-adic order
In number theory, for a given prime number p, the p-adic order or additive p-adic valuation of a number n is the highest exponent ν such that pν divides n. It is commonly abbreviated νp. The most important application of the p-adic order is in constructing the field of p-adic numbers...
on the rational numbers. This metric space is complete in the sense that every Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
converges to a point in Qp. This is what allows the development of calculus on Qp, and it is the interaction of this analytic and algebraic structure which gives the p-adic number systems their power and utility.
The p in p-adic is a variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
and may be replaced with a constant
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
(yielding, for instance, "the 2-adic numbers") or another placeholder variable (for expressions such as "the ℓ-adic numbers").
Introduction
This section is an informal introduction to p-adic numbers, using examples from the ring of 10-adic numbers. (Base 10 was chosen to highlight the analogy with decimals. The 10-adic numbers are generally not used in mathematics: since 10 is not prime, the 10-adics are not a field.) More formal constructions and properties are given below.In the standard decimal representation, almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s do not have a terminating decimal representation. For example, 1/3 is represented as a non-terminating decimal as follows

Informally, non-terminating decimals are easily understood, because it is clear that a real number can be approximated to any required degree of precision
Accuracy and precision
In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...
by a terminating decimal. If two decimal expansions differ only after the 10th decimal place, they are quite close to one another; and if they differ only after the 20th decimal place, they are even closer.
10-adic numbers use a similar non-terminating expansion, but with a different concept of "closeness" called a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
. Whereas two decimal expansions are close to one another if they differ by a large negative power of 10, two 10-adic expansions are close if they differ by a large positive power of 10. Thus 3333 and 4333, which differ by 103, are close in the 10-adic metric, and 33333333 and 43333333 are even closer, differing by 107.
In the 10-adic metric, the following sequence of numbers gets closer and closer to −1:


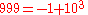
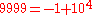
and taking this sequence to its limit, we can say (informally) that the 10-adic expansion of −1 is
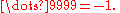
In this notation, 10-adic expansions can be extended indefinitely to the left, in contrast to decimal expansions, which can be extended indefinitely to the right. Note that this is not the only way to write p-adic numbers—for alternatives see the Notation section below.
More formally, a 10-adic number can be defined as

where each of the ai is a digit
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
taken from the set {0, 1, …..., 9} and the initial index n may be positive, negative or 0, but must be finite. From this definition, it is clear that positive integers and positive rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s with terminating decimal expansions will have terminating 10-adic expansions that are identical to their decimal expansions. Other numbers may have non-terminating 10-adic expansions.
It is possible to define addition, subtraction, and multiplication on 10-adic numbers in a consistent way, so that the 10-adic numbers form a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
.
We can create 10-adic expansions for negative numbers as follows
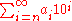

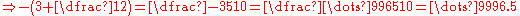
and fractions which have non-terminating decimal expansions also have non-terminating 10-adic expansions. For example
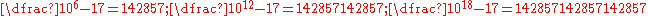

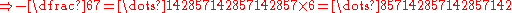

Generalizing the last example, we can find a 10-adic expansion for any rational number p⁄q such that q is co-prime to 10; Euler's theorem guarantees that if q is co-prime to 10, then there is an n such that 10n − 1 is a multiple of q.
However, 10-adic numbers have one major drawback. It is possible to find pairs of non-zero 10-adic numbers whose product is 0. In other words, the 10-adic numbers are not a domain because they contain zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s. This turns out to be because 10 is a composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
which is not a power of a prime. This problem is avoided by using a prime number p as the base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
of the number system instead of 10.
p-adic expansions
If p is a fixed prime number, then any positive integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
can be written in a base p expansion in the form

where the ai are integers in {0, …, p − 1}. For example, the binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
expansion of 35 is 1·25 + 0·24 + 0·23 + 0·22 + 1·21 + 1·20, often written in the shorthand notation 1000112.
The familiar approach to extending this description to the larger domain of the rationals (and, ultimately, to the reals) is to use sums of the form:

A definite meaning is given to these sums based on Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s, using the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
as metric. Thus, for example, 1/3 can be expressed in base 5 as the limit of the sequence 0.1313131313...5. In this formulation, the integers are precisely those numbers for which ai = 0 for all i < 0.
As an alternative, if we extend the base p expansions by allowing infinite sums of the form
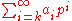
where k is some (not necessarily positive) integer, we obtain the p-adic expansions defining the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
Qp of p-adic numbers. Those p-adic numbers for which ai = 0 for all i < 0 are also called the p-adic integers. The p-adic integers form a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of Qp, denoted Zp. (Not to be confused with the ring of integers modulo p which is also sometimes written Zp. To avoid ambiguity, Z/pZ or Z/(p) are often used to represent the integers modulo p.)
Intuitively, as opposed to p-adic expansions which extend to the right as sums of ever smaller, increasingly negative powers of the base p (as is done for the real numbers as described above), these are numbers whose p-adic expansion to the left are allowed to go on forever. For example, the p-adic expansion of 1/3 in base 5 is …1313132, i.e. the limit of the sequence 2, 32, 132, 3132, 13132, 313132, 1313132,… . Multiplying this infinite sum by 3 in base 5 gives …0000001. As there are no negative powers of 5 in this expansion of 1/3 (i.e. no numbers to the right of the decimal point), we see that 1/3 is a p-adic integer in base 5.
While it is possible to use this approach to rigorously define p-adic numbers and explore their properties, just as in the case of real numbers other approaches are generally preferred. Hence we want to define a notion of infinite sum which makes these expressions meaningful, and this is most easily accomplished by the introduction of the p-adic metric. Two different but equivalent solutions to this problem are presented in the Constructions section below.
Notation
There are several different conventions for writing p-adic expansions. So far this article has used a notation for p-adic expansions in which powersExponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of p increase from right to left. With this right-to-left notation the 3-adic expansion of 1/5, for example, is written as
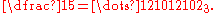
When performing arithmetic in this notation, digits are carried to the left. It is also possible to write p-adic expansions so that the powers of p increase from left to right, and digits are carried to the right. With this left-to-right notation the 3-adic expansion of 1/5 is
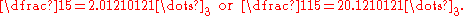
p-adic expansions may be written with other sets of digits instead of {0, 1, …, p − 1}. For example, the 3-adic expansion of 1/5 can be written using balanced ternary
Balanced ternary
Balanced ternary is a non-standard positional numeral system , useful for comparison logic. It is a ternary system, but unlike the standard ternary system, the digits have the values −1, 0, and 1...
digits {1,0,1} as

In fact any set of p integers which are in distinct residue classes modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
p may be used as p-adic digits. In number theory, Teichmüller digits are sometimes used.
Analytic approach
The real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s can be defined as equivalence classes of Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s; this allows us to, for example, write 1 as 1.000… = 0.999… . The definition of a Cauchy sequence relies on the metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
chosen, though, so if we choose a different one, we can construct numbers other than the real numbers. The usual metric which yields the real numbers is called the Euclidean metric.
For a given prime p, we define the p-adic absolute value in Q as follows:
for any non-zero rational number x, there is a unique integer n allowing us to write x = pn(a/b), where neither of the integers a and b is divisible
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
by p. Unless the numerator or denominator of x in lowest terms contains p as a factor, n will be 0. Now define |x|p = p−n. We also define |0|p = 0.
For example with x = 63/550 = 2−1 32 5−2 7 11−1
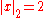


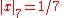


This definition of |x|p has the effect that high powers of p become "small".
By the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
, for a given non-zero rational number x there is a unique finite set of distinct primes
 and a corresponding sequence of non-zero integers
and a corresponding sequence of non-zero integers  such that:
such that: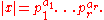
It then follows that
 for all
for all 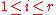 , and
, and 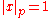 for any other prime
for any other prime 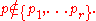
It is a theorem of Ostrowski
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
that each absolute value
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
on Q is equivalent either to the Euclidean absolute value, the trivial absolute value, or to one of the p-adic absolute values for some prime p. The p-adic absolute value defines a metric dp on Q by setting

The field Qp of p-adic numbers can then be defined as the completion of the metric space (Q,dp); its elements are equivalence classes of Cauchy sequences, where two sequences are called equivalent if their difference converges to zero. In this way, we obtain a complete metric space which is also a field and contains Q.
It can be shown that in Qp, every element x may be written in a unique way as
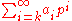
where k is some integer and each ai is in {0, …, p − 1}. This series converges
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
to x with respect to the metric dp.
With this absolute value, the field Qp is a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
.
Algebraic approach
In the algebraic approach, we first define the ring of p-adic integers, and then construct the field of fractions of this ring to get the field of p-adic numbers.We start with the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the rings
Z/pnZ (see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
): a p-adic integer is then a sequence
(an)n≥1 such that an is in
Z/pnZ, and if n ≤ m, then
an ≡ am (mod pn).
Every natural number m defines such a sequence (an) by an = m mod pn and can therefore be regarded as a p-adic integer. For example, in this case 35 as a 2-adic integer would be written as the sequence (1, 3, 3, 3, 3, 35, 35, 35, …).
The operators of the ring amount to pointwise addition and multiplication of such sequences. This is well defined because addition and multiplication commute with the mod operator, see modular arithmetic.
Moreover, every sequence (an) where the first element is not 0 has an inverse. In that case, for every n, an and p are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
, and so an and pn are relatively prime. Therefore, each an has an inverse mod pn, and the sequence of these inverses, (bn), is the sought inverse of (an). For example, consider the p-adic integer corresponding to the natural number 7; as a 2-adic number, it would be written (1, 3, 7, 7, 7, 7, 7, ...). This object's inverse would be written as an ever-increasing sequence that begins (1, 3, 7, 7, 23, 55, 55, 183, 439, 439, 1463 ...). Naturally, this 2-adic integer has no corresponding natural number.
Every such sequence can alternatively be written as a series of the form we considered above. For instance, in the 3-adics, the sequence (2, 8, 8, 35, 35, ...) can be written as 2 + 2·3 + 0·32 + 1·33 + 0·34 + ... The partial sums of this latter series are the elements of the given sequence.
The ring of p-adic integers has no zero divisors, so we can take the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
to get the field Qp of p-adic numbers. Note that in this field of fractions, every non-integer p-adic number can be uniquely written as p−nu with a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n and a unit in the p-adic integers u. This means that
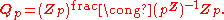
Note that
 , where
, where 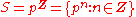 is a multiplicative subset (contains the unit and closed under multiplication) of a commutative ring with unit
is a multiplicative subset (contains the unit and closed under multiplication) of a commutative ring with unit  , is an algebraic construction called the ring of fractions of
, is an algebraic construction called the ring of fractions of  by
by 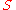 .
.Properties
The ring of p-adic integers is the inverse limitInverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the finite rings Z/pkZ, but is nonetheless uncountable
Uncountable set
In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
, and has the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
. Accordingly, the field Qp is uncountable. The endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of the Prüfer p-group
Prüfer group
In mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z, for a prime number p is the unique p-group in which every element has p pth roots. The group is named after Heinz Prüfer...
of rank n, denoted Z(p∞)n, is the ring of n×n matrices over the p-adic integers; this is sometimes referred to as the Tate module
Tate module
In mathematics, a Tate module of an abelian group, named for John Tate, is a module constructed from an abelian group A. Often, this construction is made in the following situation: G is a commutative group scheme over a field K, Ks is the separable closure of K, and A = G...
.
The p-adic numbers contain the rational numbers Q and form a field of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0. This field cannot be turned into an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
.
Let the topology τ on Zp be defined by taking as a basis all sets of the form Ua(n) = {n + λ pa for λ in Zp and a in N}. Then Zp is a compactification
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
of Z, under the derived topology (it is not a compactification of Z with its usual topology). The relative topology on Z as a subset of Zp is called the p-adic topology on Z.
The topology of the set of p-adic integers is that of a Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
; the topology of the set of p-adic numbers is that of a Cantor set minus a point (which would naturally be called infinity). In particular, the space of p-adic integers is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
while the space of p-adic numbers is not; it is only locally compact.
As metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, both the p-adic integers and the p-adic numbers are complete.
The real numbers have only a single proper algebraic extension
Algebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
, the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s; in other words, this quadratic extension is already algebraically closed
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
. By contrast, the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the p-adic numbers has infinite degree. Furthermore, Qp has infinitely many inequivalent algebraic extensions. Also contrasting the case of real numbers, the algebraic closure of Qp is not (metrically) complete. Its (metric) completion is called Cp. Here an end is reached, as Cp is algebraically closed.
The field Cp is isomorphic to the field C of complex numbers, so we may regard Cp as the complex numbers endowed with an exotic metric. It should be noted that the proof of existence of such a field isomorphism relies on the axiom of choice, and does not provide an explicit example of such an isomorphism.
The p-adic numbers contain the nth cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
(n>2) if and only if n divides p − 1. For instance, the nth cyclotomic field is a subfield of Q13 if and only if n = 1, 2, 3, 4, 6, or 12. In particular, there is no multiplicative p-torsion in the p-adic numbers, if p > 2. Also, -1 is the only non-trivial torsion element in 2-adic numbers.
Given a natural number k, the index of the multiplicative group of the k-th powers of the non-zero elements of Qp in the multiplicative group of Qp is finite.
The number e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, defined as the sum of reciprocals of factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s, is not a member of any p-adic field; but ep is a p-adic number for all p except 2, for which one must take at least the fourth power. (Thus a number with similar properties as e - namely a pth root of ep - is a member of the algebraic closure of the p-adic numbers for all p.)
Over the reals, the only functions whose derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is zero are the constant functions. This is not true over Qp. For instance, the function
- f: Qp → Qp, f(x) = (1/|x|p)2 for x ≠ 0, f(0) = 0,
has zero derivative everywhere but is not even locally constant
Locally constant function
In mathematics, a function f from a topological space A to a set B is called locally constant, if for every a in A there exists a neighborhood U of a, such that f is constant on U....
at 0.
Given any elements r∞, r2, r3, r5, r7, ... where rp is in Qp (and Q∞ stands for R), it is possible to find a sequence (xn) in Q such that for all p (including ∞), the limit of xn in Qp is rp.
The field Qp is a locally compact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
If
 is a finite Galois extension
is a finite Galois extensionGalois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of
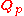 ,
,the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
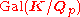 is solvable
is solvableSolvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
.
Thus, the Galois group
 is prosolvable.
is prosolvable.Rational arithmetic
Hehner and Horspool proposed in 1979 the use of a p-adic representation for rational numbers on computers. The primary advantage of such a representation is that addition, subtraction, and multiplication can be done in a straightforward manner analogous to similar methods for binary integers; and division is even simpler, resembling multiplication. However, it has the disadvantage that representations can be much larger than simply storing the numerator and denominator in binary; for example, if 2n−1 is a Mersenne primeMersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
, its reciprocal will require 2n−1 bits to represent.
Generalizations and related concepts
The reals and the p-adic numbers are the completions of the rationals; it is also possible to complete other fields, for instance general algebraic number fieldAlgebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s, in an analogous way. This will be described now.
Suppose D is a Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
and E is its field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
. Pick a non-zero prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
P of D. If x is a non-zero element of E, then xD is a fractional ideal
Fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
and can be uniquely factored as a product of positive and negative powers of non-zero prime ideals of D. We write ordP(x) for the exponent of P in this factorization, and for any choice of number c greater than 1 we can set

Completing with respect to this absolute value |.|P yields a field EP, the proper generalization of the field of p-adic numbers to this setting.
The choice of c does not change the completion (different choices yield the same concept of Cauchy sequence, so the same completion).
It is convenient, when the residue field
Residue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
D/P is finite, to take for c the size of D/P.
For example, when E is a number field, Ostrowski's theorem
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
says that every non-trivial non-Archimedean absolute value
Absolute value (algebra)
In mathematics, an absolute value is a function which measures the "size" of elements in a field or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:* | x | ≥ 0,*...
on E arises as some |.|P. The remaining non-trivial absolute values
on E arise from the different embeddings of E into the real or complex numbers. (In fact, the non-Archimedean absolute values can be considered as simply the different embeddings of E into the fields Cp, thus putting the description of all
the non-trivial absolute values of a number field on a common footing.)
Often, one needs to simultaneously keep track of all the above mentioned completions when E is a number field (or more generally a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
), which are seen as encoding "local" information. This is accomplished by adele ring
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
s and idele groups.
Local-global principle
Helmut HasseHelmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
's local-global principle is said to hold for an equation if it can be solved over the rational numbers if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it can be solved over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s and over the p-adic numbers for every prime p.
External links
- p-adic number at Springer On-line Encyclopaedia of MathematicsEncyclopaedia of MathematicsThe Encyclopaedia of Mathematics is a large reference work in mathematics. It is available in book form and on CD-ROM....
- Completion of Algebraic Closure - on-line lecture notes by Brian Conrad
- An Introduction to p-adic Numbers and p-adic Analysis - on-line lecture notes by Andrew Baker, 2007

