Zeno's paradoxes
Encyclopedia
Zeno's paradoxes are a set of problems generally thought to have been devised by Greek
philosopher Zeno of Elea
(ca. 490 - 430 BC) to support Parmenides's
doctrine that "all is one" and that, contrary to the evidence of our senses, the belief in plurality and change is mistaken, and in particular that motion
is nothing but an illusion
. It is usually assumed, based on Plato's
Parmenides 128c-d, that Zeno took on the project of creating these paradox
es because other philosophers had created paradoxes against Parmenides's view. Thus Zeno can be interpreted as saying that to assume there is plurality is even more absurd than assuming there is only "the One". (Parmenides 128d). Plato makes Socrates
claim that Zeno and Parmenides were essentially arguing exactly the same point (Parmenides 128a-b).
Some of Zeno's nine surviving paradoxes (preserved in Aristotle's
Physics
and Simplicius's
commentary thereon) are essentially equivalent to one another. Aristotle offered a refutation of some of them. Three of the strongest and most famous—that of Achilles
and the tortoise
, the Dichotomy
argument, and that of an arrow in flight—are presented in detail below.
Zeno's arguments are perhaps the first examples of a method of proof called reductio ad absurdum
also known as proof by contradiction. They are also credited as a source of the dialectic
method used by Socrates
.
Some mathematicians, such as Carl Boyer, hold that Zeno's paradoxes are simply mathematical problems, for which modern calculus
provides a mathematical solution.
Some philosophers, however, say that Zeno's paradoxes and their variations (see Thomson's lamp
) remain relevant metaphysical
problems.
The origins of the paradoxes are somewhat unclear. Diogenes Laertius
, a fourth source for information about Zeno and his teachings, citing Favorinus
, says that Zeno's teacher Parmenides
, was the first to introduce the Achilles and the Tortoise Argument. But in a later passage, Laertius attributes the origin of the paradox to Zeno, explaining that Favorinus disagrees.
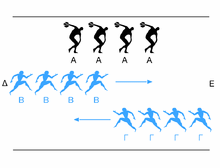
and the Tortoise
, Achilles is in a footrace with the tortoise. Achilles allows the tortoise a head start
of 100 metres, for example. If we suppose that each racer starts running at some constant speed (one very fast and one very slow), then after some finite time
, Achilles will have run 100 metres, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say, 10 metres. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles reaches somewhere the tortoise has been, he still has farther to go. Therefore, because there are an infinite number of points Achilles must reach where the tortoise has already been, he can never overtake the tortoise.

The resulting sequence can be represented as:
This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility.
This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can neither be completed nor begun, and so all motion must be an illusion
.
This argument is called the Dichotomy
because it involves repeatedly splitting a distance into two parts. It contains some of the same elements as the Achilles and the Tortoise paradox, but with a more apparent conclusion of motionlessness. It is also known as the Race Course paradox. Some, like Aristotle, regard the Dichotomy as really just another version of Achilles and the Tortoise.
There are two versions of the dichotomy paradox. In the other version, before Homer could reach the stationary bus, he must reach half of the distance to it. Before reaching the last half, he must complete the next quarter of the distance. Reaching the next quarter, he must then cover the next eighth of the distance, then the next sixteenth, and so on. There are thus an infinite number of steps that must first be accomplished before he could reach the bus, with no way to establish the size of any "last" step. Expressed this way, the dichotomy paradox is very much analogous to that of Achilles and the tortoise.
paradox), Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that in any one (durationless) instant of time, the arrow is neither moving to where it is, nor to where it is not.
It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.
Whereas the first two paradoxes presented divide space, this paradox starts by dividing time—and not into segments, but into points.
Paradox of the Grain of Millet:
The Moving Rows (or Stadium):
For an expanded account of Zeno's arguments as presented by Aristotle, see Simplicius'
commentary On Aristotle's Physics.
, Diogenes the Cynic said nothing upon hearing Zeno's arguments, but stood up and walked, in order to demonstrate the falsity of Zeno's conclusions. To fully solve any of the paradoxes, however, one needs to show what is wrong with the argument, not just the conclusions. Through history, several solutions have been proposed, among the earliest recorded being those of Aristotle and Archimedes.
Aristotle
(384 BC−322 BC) remarked that as the distance decreases, the time needed to cover those distances also decreases, so that the time needed also becomes increasingly small.
Aristotle also distinguished "things infinite in respect of divisibility" (such as a unit of space that can be mentally divided into ever smaller units while remaining spatially the same) from things (or distances) that are infinite in extension ("with respect to their extremities").
Before 212 BC, Archimedes
had developed a method to derive a finite answer for the sum of infinitely many terms that get progressively smaller. (See: Geometric series, 1/4 + 1/16 + 1/64 + 1/256 + · · ·
, The Quadrature of the Parabola
.) Modern calculus achieves the same result, using more rigorous methods (see convergent series, where the "reciprocals of powers of 2" series, equivalent to the Dichotomy Paradox, is listed as convergent). These methods allow the construction of solutions based on the conditions stipulated by Zeno, i.e. the amount of time taken at each step is geometrically decreasing.
Aristotle's objection to the arrow paradox was that "Time is not composed of indivisible nows any more than any other magnitude is composed of indivisibles."
Saint Thomas Aquinas, commenting on Aristotle's objection, wrote "Instants are not parts of time, for time is not made up of instants any more than a magnitude is made of points, as we have already proved. Hence it does not follow that a thing is not in motion in a given time, just because it is not in motion in any instant of that time."
Bertrand Russell
offered what is known as the "at-at theory of motion". It agrees that there can be no motion "during" a durationless instant, and contends that all that is required for motion is that the arrow be at one point at one time, at another point another time, and at appropriate points between those two points for intervening times. In this view motion is a function of position with respect to time.
Nick Huggett argues that Zeno is begging the question
when he says that objects that occupy the same space as they do at rest must be at rest.
Peter Lynds
has argued that all of Zeno's motion paradoxes are resolved by the conclusion that instants in time and instantaneous magnitudes do not actually exist.
Lynds argues that an object in relative motion cannot have a determined relative position (for if it did, it could not be in motion), and so cannot have its motion fractionally dissected as though it does as in the paradoxes.
Another proposed solution is to question one of the assumptions of Zeno used in his paradoxes (particularly the Dichotomy), which is that between any two different points in space (or time), there is always another point. Without this assumption there are only a finite number of distances between two points, hence there is no infinite sequence of movements, and the paradox is resolved. The ideas of Planck length and Planck time
in modern physics place a limit on the measurement of time and space, if not on time and space themselves. According to Hermann Weyl
, the assumption that space is made of finite and discrete units is subject to a further problem, given by the "tile argument" or "distance function problem".
According to this, the length of the hypotenuse of a right angled triangle in discretized space is always equal to the length of one of the two sides, in contradiction to geometry. Jean Paul van Bendegem has argued that the Tile Argument can be resolved, and that discretization can therefore remove the paradox.
Hans Reichenbach
has proposed that the paradox may arise from considering space and time as separate entities. In a theory like general relativity, which presumes a single space-time continuum, the paradox may be blocked.
and Cauchy
developed a rigorous formulation of the logic and calculus involved. These works resolved the mathematics involving infinite processes.
While mathematics can be used to calculate where and when the moving Achilles will overtake the Tortoise of Zeno's paradox, philosophers such as Brown and Moorcroft
claim that mathematics does not address the central point in Zeno's argument, and that solving the mathematical issues does not solve every issue the paradoxes raise.
Zeno's arguments are often misrepresented in the popular literature. That is, Zeno is often said to have argued that the sum of an infinite number of terms must itself be infinite–with the result that not only the time, but also the distance to be travelled, become infinite. However, none of the original ancient sources has Zeno discussing the sum of any infinite series. Simplicius has Zeno saying "it is impossible to traverse an infinite number of things in a finite time". This presents Zeno's problem not with finding the sum, but rather with finishing a task with an infinite number of steps: how can one ever get from A to B, if an infinite number of (non-instantaneous) events can be identified that need to precede the arrival at B, and one cannot reach even the beginning of a "last event"?
Today there is still a debate on the question of whether or not Zeno's paradoxes have been resolved. In The History of Mathematics, Burton writes, "Although Zeno's argument confounded his contemporaries, a satisfactory explanation incorporates a now-familiar idea, the notion of a 'convergent infinite series.'"
Bertrand Russell
offered a "solution" to the paradoxes based on modern physics, but Brown concludes "Given the history of 'final resolutions', from Aristotle onwards, it's probably foolhardy to think we've reached the end. It may be that Zeno's arguments on motion, because of their simplicity and universality, will always serve as a kind of 'Rorschach image'
onto which people can project their most fundamental phenomenological concerns (if they have any)."
physicists E. C. G. Sudarshan and B. Misra studying quantum mechanics discovered that the dynamical evolution (motion) of a quantum system can be hindered (or even inhibited) through observation of the system.
This effect is usually called the "quantum Zeno effect" as it is strongly reminiscent of Zeno's arrow paradox.
This effect was first theorized in 1958.
and hybrid systems, the system behaviour is called Zeno if it includes an infinite number of discrete steps in a finite amount of time.
Some formal verification
techniques exclude these behaviours from analysis, if they are not equivalent to non-Zeno behaviour.
In systems design
these behaviours will also often be excluded from system models, since they cannot be implemented with a digital controller.
A simple example of a system showing Zeno behavior is a bouncing ball coming to rest. The physics of a bouncing ball can be mathematically analyzed in such a way, ignoring factors other than rebound, to predict an infinite number of bounces.
Greek
Greek may refer to anything related to:*Greece, a country in south-eastern Europe*Greeks, an ethnic group*Greek language, or more specifically:**Mycenaean Greek, **Ancient Greek,...
philosopher Zeno of Elea
Zeno of Elea
Zeno of Elea was a pre-Socratic Greek philosopher of southern Italy and a member of the Eleatic School founded by Parmenides. Aristotle called him the inventor of the dialectic. He is best known for his paradoxes, which Bertrand Russell has described as "immeasurably subtle and profound".- Life...
(ca. 490 - 430 BC) to support Parmenides's
Parmenides
Parmenides of Elea was an ancient Greek philosopher born in Elea, a Greek city on the southern coast of Italy. He was the founder of the Eleatic school of philosophy. The single known work of Parmenides is a poem, On Nature, which has survived only in fragmentary form. In this poem, Parmenides...
doctrine that "all is one" and that, contrary to the evidence of our senses, the belief in plurality and change is mistaken, and in particular that motion
Motion (physics)
In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
is nothing but an illusion
Illusion
An illusion is a distortion of the senses, revealing how the brain normally organizes and interprets sensory stimulation. While illusions distort reality, they are generally shared by most people....
. It is usually assumed, based on Plato's
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
Parmenides 128c-d, that Zeno took on the project of creating these paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
es because other philosophers had created paradoxes against Parmenides's view. Thus Zeno can be interpreted as saying that to assume there is plurality is even more absurd than assuming there is only "the One". (Parmenides 128d). Plato makes Socrates
Socrates
Socrates was a classical Greek Athenian philosopher. Credited as one of the founders of Western philosophy, he is an enigmatic figure known chiefly through the accounts of later classical writers, especially the writings of his students Plato and Xenophon, and the plays of his contemporary ...
claim that Zeno and Parmenides were essentially arguing exactly the same point (Parmenides 128a-b).
Some of Zeno's nine surviving paradoxes (preserved in Aristotle's
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
Physics
Physics (Aristotle)
The Physics of Aristotle is one of the foundational books of Western science and philosophy...
and Simplicius's
Simplicius of Cilicia
Simplicius of Cilicia, was a disciple of Ammonius Hermiae and Damascius, and was one of the last of the Neoplatonists. He was among the pagan philosophers persecuted by Justinian in the early 6th century, and was forced for a time to seek refuge in the Persian court, before being allowed back into...
commentary thereon) are essentially equivalent to one another. Aristotle offered a refutation of some of them. Three of the strongest and most famous—that of Achilles
Achilles
In Greek mythology, Achilles was a Greek hero of the Trojan War, the central character and the greatest warrior of Homer's Iliad.Plato named Achilles the handsomest of the heroes assembled against Troy....
and the tortoise
Tortoise
Tortoises are a family of land-dwelling reptiles of the order of turtles . Like their marine cousins, the sea turtles, tortoises are shielded from predators by a shell. The top part of the shell is the carapace, the underside is the plastron, and the two are connected by the bridge. The tortoise...
, the Dichotomy
Dichotomy
A dichotomy is any splitting of a whole into exactly two non-overlapping parts, meaning it is a procedure in which a whole is divided into two parts...
argument, and that of an arrow in flight—are presented in detail below.
Zeno's arguments are perhaps the first examples of a method of proof called reductio ad absurdum
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
also known as proof by contradiction. They are also credited as a source of the dialectic
Dialectic
Dialectic is a method of argument for resolving disagreement that has been central to Indic and European philosophy since antiquity. The word dialectic originated in Ancient Greece, and was made popular by Plato in the Socratic dialogues...
method used by Socrates
Socrates
Socrates was a classical Greek Athenian philosopher. Credited as one of the founders of Western philosophy, he is an enigmatic figure known chiefly through the accounts of later classical writers, especially the writings of his students Plato and Xenophon, and the plays of his contemporary ...
.
Some mathematicians, such as Carl Boyer, hold that Zeno's paradoxes are simply mathematical problems, for which modern calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
provides a mathematical solution.
Some philosophers, however, say that Zeno's paradoxes and their variations (see Thomson's lamp
Thomson's lamp
Thomson's lamp is a puzzle that is a variation on Zeno's paradoxes. It was devised by philosopher James F. Thomson, who also coined the term supertask....
) remain relevant metaphysical
Metaphysics
Metaphysics is a branch of philosophy concerned with explaining the fundamental nature of being and the world, although the term is not easily defined. Traditionally, metaphysics attempts to answer two basic questions in the broadest possible terms:...
problems.
The origins of the paradoxes are somewhat unclear. Diogenes Laertius
Diogenes Laertius
Diogenes Laertius was a biographer of the Greek philosophers. Nothing is known about his life, but his surviving Lives and Opinions of Eminent Philosophers is one of the principal surviving sources for the history of Greek philosophy.-Life:Nothing is definitively known about his life...
, a fourth source for information about Zeno and his teachings, citing Favorinus
Favorinus
Favorinus of Arelata was a Roman sophist and philosopher who flourished during the reign of Hadrian.He was of Gaulish ancestry, born in Arelate . He is described as a hermaphrodite by birth...
, says that Zeno's teacher Parmenides
Parmenides
Parmenides of Elea was an ancient Greek philosopher born in Elea, a Greek city on the southern coast of Italy. He was the founder of the Eleatic school of philosophy. The single known work of Parmenides is a poem, On Nature, which has survived only in fragmentary form. In this poem, Parmenides...
, was the first to introduce the Achilles and the Tortoise Argument. But in a later passage, Laertius attributes the origin of the paradox to Zeno, explaining that Favorinus disagrees.
Achilles and the tortoise
In the paradox of AchillesAchilles
In Greek mythology, Achilles was a Greek hero of the Trojan War, the central character and the greatest warrior of Homer's Iliad.Plato named Achilles the handsomest of the heroes assembled against Troy....
and the Tortoise
Tortoise
Tortoises are a family of land-dwelling reptiles of the order of turtles . Like their marine cousins, the sea turtles, tortoises are shielded from predators by a shell. The top part of the shell is the carapace, the underside is the plastron, and the two are connected by the bridge. The tortoise...
, Achilles is in a footrace with the tortoise. Achilles allows the tortoise a head start
Head start (positioning)
In positioning, a head start is a start in advance of the starting position of others in competition, or simply toward the finish line or desired outcome...
of 100 metres, for example. If we suppose that each racer starts running at some constant speed (one very fast and one very slow), then after some finite time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, Achilles will have run 100 metres, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say, 10 metres. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles reaches somewhere the tortoise has been, he still has farther to go. Therefore, because there are an infinite number of points Achilles must reach where the tortoise has already been, he can never overtake the tortoise.
The dichotomy paradox
Suppose Homer wants to catch a stationary bus. Before he can get there, he must get halfway there. Before he can get halfway there, he must get a quarter of the way there. Before traveling a quarter, he must travel one-eighth; before an eighth, one-sixteenth; and so on.
The resulting sequence can be represented as:

This description requires one to complete an infinite number of tasks, which Zeno maintains is an impossibility.
This sequence also presents a second problem in that it contains no first distance to run, for any possible (finite) first distance could be divided in half, and hence would not be first after all. Hence, the trip cannot even begin. The paradoxical conclusion then would be that travel over any finite distance can neither be completed nor begun, and so all motion must be an illusion
Illusion
An illusion is a distortion of the senses, revealing how the brain normally organizes and interprets sensory stimulation. While illusions distort reality, they are generally shared by most people....
.
This argument is called the Dichotomy
Dichotomy
A dichotomy is any splitting of a whole into exactly two non-overlapping parts, meaning it is a procedure in which a whole is divided into two parts...
because it involves repeatedly splitting a distance into two parts. It contains some of the same elements as the Achilles and the Tortoise paradox, but with a more apparent conclusion of motionlessness. It is also known as the Race Course paradox. Some, like Aristotle, regard the Dichotomy as really just another version of Achilles and the Tortoise.
There are two versions of the dichotomy paradox. In the other version, before Homer could reach the stationary bus, he must reach half of the distance to it. Before reaching the last half, he must complete the next quarter of the distance. Reaching the next quarter, he must then cover the next eighth of the distance, then the next sixteenth, and so on. There are thus an infinite number of steps that must first be accomplished before he could reach the bus, with no way to establish the size of any "last" step. Expressed this way, the dichotomy paradox is very much analogous to that of Achilles and the tortoise.
The arrow paradox
In the arrow paradox (also known as the fletcher'sFletching
Fletching is the aerodynamic stabilization of arrows or darts with materials such as feathers, each piece of which is referred to as a fletch. The word is related to the French word flèche, meaning "arrow," via Old French; the ultimate root is Frankish fliukka...
paradox), Zeno states that for motion to occur, an object must change the position which it occupies. He gives an example of an arrow in flight. He states that in any one (durationless) instant of time, the arrow is neither moving to where it is, nor to where it is not.
It cannot move to where it is not, because no time elapses for it to move there; it cannot move to where it is, because it is already there. In other words, at every instant of time there is no motion occurring. If everything is motionless at every instant, and time is entirely composed of instants, then motion is impossible.
Whereas the first two paradoxes presented divide space, this paradox starts by dividing time—and not into segments, but into points.
Three other paradoxes as given by Aristotle
Paradox of Place:- "… if everything that exists has a place, place too will have a place, and so on ad infinitumAd infinitumAd infinitum is a Latin phrase meaning "to infinity."In context, it usually means "continue forever, without limit" and thus can be used to describe a non-terminating process, a non-terminating repeating process, or a set of instructions to be repeated "forever," among other uses...
."
Paradox of the Grain of Millet:
- "… there is no part of the millet that does not make a sound: for there is no reason why any such part should not in any length of time fail to move the air that the whole bushel moves in falling. In fact it does not of itself move even such a quantity of the air as it would move if this part were by itself: for no part even exists otherwise than potentially."
The Moving Rows (or Stadium):
- "The fourth argument is that concerning the two rows of bodies, each row being composed of an equal number of bodies of equal size, passing each other on a race-course as they proceed with equal velocity in opposite directions, the one row originally occupying the space between the goal and the middle point of the course and the other that between the middle point and the starting-post. This...involves the conclusion that half a given time is equal to double that time."
For an expanded account of Zeno's arguments as presented by Aristotle, see Simplicius'
Simplicius of Cilicia
Simplicius of Cilicia, was a disciple of Ammonius Hermiae and Damascius, and was one of the last of the Neoplatonists. He was among the pagan philosophers persecuted by Justinian in the early 6th century, and was forced for a time to seek refuge in the Persian court, before being allowed back into...
commentary On Aristotle's Physics.
Proposed solutions
According to SimpliciusSimplicius of Cilicia
Simplicius of Cilicia, was a disciple of Ammonius Hermiae and Damascius, and was one of the last of the Neoplatonists. He was among the pagan philosophers persecuted by Justinian in the early 6th century, and was forced for a time to seek refuge in the Persian court, before being allowed back into...
, Diogenes the Cynic said nothing upon hearing Zeno's arguments, but stood up and walked, in order to demonstrate the falsity of Zeno's conclusions. To fully solve any of the paradoxes, however, one needs to show what is wrong with the argument, not just the conclusions. Through history, several solutions have been proposed, among the earliest recorded being those of Aristotle and Archimedes.
Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
(384 BC−322 BC) remarked that as the distance decreases, the time needed to cover those distances also decreases, so that the time needed also becomes increasingly small.
Aristotle also distinguished "things infinite in respect of divisibility" (such as a unit of space that can be mentally divided into ever smaller units while remaining spatially the same) from things (or distances) that are infinite in extension ("with respect to their extremities").
Before 212 BC, Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
had developed a method to derive a finite answer for the sum of infinitely many terms that get progressively smaller. (See: Geometric series, 1/4 + 1/16 + 1/64 + 1/256 + · · ·
1/4 + 1/16 + 1/64 + 1/256 + · · ·
In mathematics, the infinite series 1/4 + 1/16 + 1/64 + 1/256 + · · · is an example of one of the first infinite series to be summed in the history of mathematics; it was used by Archimedes circa 250–200 BC. Its sum is 1/3...
, The Quadrature of the Parabola
The Quadrature of the Parabola
The Quadrature of the Parabola is a treatise on geometry, written by Archimedes in the 3rd century BC. Written as a letter to his friend Dositheus, the work presents 24 propositions regarding parabolas, culminating in a proof that the area of a parabolic segment is 4/3 that of a certain inscribed...
.) Modern calculus achieves the same result, using more rigorous methods (see convergent series, where the "reciprocals of powers of 2" series, equivalent to the Dichotomy Paradox, is listed as convergent). These methods allow the construction of solutions based on the conditions stipulated by Zeno, i.e. the amount of time taken at each step is geometrically decreasing.
Aristotle's objection to the arrow paradox was that "Time is not composed of indivisible nows any more than any other magnitude is composed of indivisibles."
Saint Thomas Aquinas, commenting on Aristotle's objection, wrote "Instants are not parts of time, for time is not made up of instants any more than a magnitude is made of points, as we have already proved. Hence it does not follow that a thing is not in motion in a given time, just because it is not in motion in any instant of that time."
Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
offered what is known as the "at-at theory of motion". It agrees that there can be no motion "during" a durationless instant, and contends that all that is required for motion is that the arrow be at one point at one time, at another point another time, and at appropriate points between those two points for intervening times. In this view motion is a function of position with respect to time.
Nick Huggett argues that Zeno is begging the question
Begging the question
Begging the question is a type of logical fallacy in which the proposition to be proven is assumed implicitly or explicitly in the premise....
when he says that objects that occupy the same space as they do at rest must be at rest.
Peter Lynds
Peter Lynds
Peter Lynds is a New Zealander who first drew attention in 2003 with the publication of a physics paper about time, mechanics and Zeno's paradoxes....
has argued that all of Zeno's motion paradoxes are resolved by the conclusion that instants in time and instantaneous magnitudes do not actually exist.
Lynds argues that an object in relative motion cannot have a determined relative position (for if it did, it could not be in motion), and so cannot have its motion fractionally dissected as though it does as in the paradoxes.
Another proposed solution is to question one of the assumptions of Zeno used in his paradoxes (particularly the Dichotomy), which is that between any two different points in space (or time), there is always another point. Without this assumption there are only a finite number of distances between two points, hence there is no infinite sequence of movements, and the paradox is resolved. The ideas of Planck length and Planck time
Planck time
In physics, the Planck time, , is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length...
in modern physics place a limit on the measurement of time and space, if not on time and space themselves. According to Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, the assumption that space is made of finite and discrete units is subject to a further problem, given by the "tile argument" or "distance function problem".
According to this, the length of the hypotenuse of a right angled triangle in discretized space is always equal to the length of one of the two sides, in contradiction to geometry. Jean Paul van Bendegem has argued that the Tile Argument can be resolved, and that discretization can therefore remove the paradox.
Hans Reichenbach
Hans Reichenbach
Hans Reichenbach was a leading philosopher of science, educator and proponent of logical empiricism...
has proposed that the paradox may arise from considering space and time as separate entities. In a theory like general relativity, which presumes a single space-time continuum, the paradox may be blocked.
The paradoxes in modern times
Infinite processes remained theoretically troublesome in mathematics until the late 19th century. The epsilon-delta version of WeierstrassKarl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
and Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
developed a rigorous formulation of the logic and calculus involved. These works resolved the mathematics involving infinite processes.
While mathematics can be used to calculate where and when the moving Achilles will overtake the Tortoise of Zeno's paradox, philosophers such as Brown and Moorcroft
claim that mathematics does not address the central point in Zeno's argument, and that solving the mathematical issues does not solve every issue the paradoxes raise.
Zeno's arguments are often misrepresented in the popular literature. That is, Zeno is often said to have argued that the sum of an infinite number of terms must itself be infinite–with the result that not only the time, but also the distance to be travelled, become infinite. However, none of the original ancient sources has Zeno discussing the sum of any infinite series. Simplicius has Zeno saying "it is impossible to traverse an infinite number of things in a finite time". This presents Zeno's problem not with finding the sum, but rather with finishing a task with an infinite number of steps: how can one ever get from A to B, if an infinite number of (non-instantaneous) events can be identified that need to precede the arrival at B, and one cannot reach even the beginning of a "last event"?
Today there is still a debate on the question of whether or not Zeno's paradoxes have been resolved. In The History of Mathematics, Burton writes, "Although Zeno's argument confounded his contemporaries, a satisfactory explanation incorporates a now-familiar idea, the notion of a 'convergent infinite series.'"
Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
offered a "solution" to the paradoxes based on modern physics, but Brown concludes "Given the history of 'final resolutions', from Aristotle onwards, it's probably foolhardy to think we've reached the end. It may be that Zeno's arguments on motion, because of their simplicity and universality, will always serve as a kind of 'Rorschach image'
Rorschach test
The Rorschach test is a psychological test in which subjects' perceptions of inkblots are recorded and then analyzed using psychological interpretation, complex algorithms, or both. Some psychologists use this test to examine a person's personality characteristics and emotional functioning...
onto which people can project their most fundamental phenomenological concerns (if they have any)."
The quantum Zeno effect
In 1977,physicists E. C. G. Sudarshan and B. Misra studying quantum mechanics discovered that the dynamical evolution (motion) of a quantum system can be hindered (or even inhibited) through observation of the system.
This effect is usually called the "quantum Zeno effect" as it is strongly reminiscent of Zeno's arrow paradox.
This effect was first theorized in 1958.
Zeno behavior
In the field of verification and design of timedTimed event system
The General System has been described in [Zeigler76] and [ZPK00] with the stand points to define the time base, the admissible input segments, the system states, the state trajectory with an admissible input segment, the output for a given state....
and hybrid systems, the system behaviour is called Zeno if it includes an infinite number of discrete steps in a finite amount of time.
Some formal verification
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
techniques exclude these behaviours from analysis, if they are not equivalent to non-Zeno behaviour.
In systems design
Systems design
Systems design is the process of defining the architecture, components, modules, interfaces, and data for a system to satisfy specified requirements. One could see it as the application of systems theory to product development...
these behaviours will also often be excluded from system models, since they cannot be implemented with a digital controller.
A simple example of a system showing Zeno behavior is a bouncing ball coming to rest. The physics of a bouncing ball can be mathematically analyzed in such a way, ignoring factors other than rebound, to predict an infinite number of bounces.
Writings about Zeno’s paradoxes
Zeno’s paradoxes have inspired many writers- Leo TolstoyLeo TolstoyLev Nikolayevich Tolstoy was a Russian writer who primarily wrote novels and short stories. Later in life, he also wrote plays and essays. His two most famous works, the novels War and Peace and Anna Karenina, are acknowledged as two of the greatest novels of all time and a pinnacle of realist...
in War and PeaceWar and PeaceWar and Peace is a novel by the Russian author Leo Tolstoy, first published in 1869. The work is epic in scale and is regarded as one of the most important works of world literature...
(Part 11,Chapter I) discusses the race of Achilles and the tortoise when critiquing "historical science". - In the dialogue "What the Tortoise Said to AchillesWhat the Tortoise Said to Achilles"What the Tortoise Said to Achilles", written by Lewis Carroll in 1895 for the philosophical journal Mind, is a brief dialogue which problematises the foundations of logic. The title alludes to one of Zeno's paradoxes of motion, in which Achilles could never overtake the tortoise in a race...
", Lewis CarrollLewis CarrollCharles Lutwidge Dodgson , better known by the pseudonym Lewis Carroll , was an English author, mathematician, logician, Anglican deacon and photographer. His most famous writings are Alice's Adventures in Wonderland and its sequel Through the Looking-Glass, as well as the poems "The Hunting of the...
describes what happens at the end of the race. The tortoise discusses with Achilles a simple deductive argument. Achilles fails in demonstrating the argument because the tortoise leads him into an infinite regression. - In Gödel, Escher, Bach by Douglas HofstadterDouglas HofstadterDouglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
, the various chapters are separated by dialogues between Achilles and the tortoise, inspired by Lewis Carroll’s works. - The Argentinian writer Jorge Luis BorgesJorge Luis BorgesJorge Francisco Isidoro Luis Borges Acevedo , known as Jorge Luis Borges , was an Argentine writer, essayist, poet and translator born in Buenos Aires. In 1914 his family moved to Switzerland where he attended school, receiving his baccalauréat from the Collège de Genève in 1918. The family...
discusses Zeno’s paradoxes many times in his work, showing their relationship with infinityInfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
. Borges also used Zeno’s paradoxes as a metaphor for some situations described by Kafka. Jorge Luis BorgesJorge Luis BorgesJorge Francisco Isidoro Luis Borges Acevedo , known as Jorge Luis Borges , was an Argentine writer, essayist, poet and translator born in Buenos Aires. In 1914 his family moved to Switzerland where he attended school, receiving his baccalauréat from the Collège de Genève in 1918. The family...
traces, in an essay entitled "Avatars of the Tortoise", the many recurrences of this paradox in works of philosophy. The successive references he traces are Agrippa the Skeptic, Thomas AquinasThomas AquinasThomas Aquinas, O.P. , also Thomas of Aquin or Aquino, was an Italian Dominican priest of the Catholic Church, and an immensely influential philosopher and theologian in the tradition of scholasticism, known as Doctor Angelicus, Doctor Communis, or Doctor Universalis...
, Hermann Lotze, F.H. Bradley and William JamesWilliam JamesWilliam James was a pioneering American psychologist and philosopher who was trained as a physician. He wrote influential books on the young science of psychology, educational psychology, psychology of religious experience and mysticism, and on the philosophy of pragmatism...
. - In Tom StoppardTom StoppardSir Tom Stoppard OM, CBE, FRSL is a British playwright, knighted in 1997. He has written prolifically for TV, radio, film and stage, finding prominence with plays such as Arcadia, The Coast of Utopia, Every Good Boy Deserves Favour, Professional Foul, The Real Thing, and Rosencrantz and...
's play JumpersJumpersJumpers is a 1972 play by Tom Stoppard. It explores and satirises the field of academic philosophy, likening it to a less-than skilful competitive gymnastics display...
, the philosopher George Moore attempts a practical disproof with bow and arrow of the Dichotomy Paradox, with disastrous consequences for the hare and the tortoise. - Harry MulischHarry MulischHarry Kurt Victor Mulisch was a Dutch author. He wrote more than 80 novels, plays, essays, poems and philosophical reflections. These have been translated into more than 20 languages....
's philosophical magnum opus, De compositie van de wereld (Amsterdam, 1980) is based on Zeno's Paradoxes mostly. Along with Herakleitos' thoughts and Cusanus' coïncidentia oppositorum they constitute the foundation for his own system of the 'octave'. - In the novel Small GodsSmall GodsSmall Gods is the thirteenth of Terry Pratchett's Discworld novels, published in 1992. It tells the origin of the god Om, and his relations with his prophet, the reformer Brutha...
by Terry PratchettTerry PratchettSir Terence David John "Terry" Pratchett, OBE is an English novelist, known for his frequently comical work in the fantasy genre. He is best known for his popular and long-running Discworld series of comic fantasy novels...
the prophet Brutha encounters several Ephebian (Greek) philosophers in the country, attempting to disprove Zeno's paradox by shooting arrows at a succession of tortoises. So far, this has resulted only in a succession of "tortoise-kabobs."
See also
- Ross-Littlewood paradox
- Incommensurable magnitudes
- Philosophy of space and timePhilosophy of space and timePhilosophy of space and time is the branch of philosophy concerned with the issues surrounding the ontology, epistemology, and character of space and time. While such ideas have been central to philosophy from its inception, the philosophy of space and time was both an inspiration for and a...
- Solvitur ambulandoSolvitur ambulandoSolvitur ambulando is a Latin term which means:* it is solved by walking* the problem is solved by a practical experimentDiogenes of Sinope, also known as "Diogenes the Cynic," is said to have replied to the argument that motion is unreal by standing up and walking away.The phrase appears early in...
- SupertaskSupertaskIn philosophy, a supertask is a quantifiably infinite number of operations that occur sequentially within a finite interval of time. Supertasks are called "hypertasks" when the number of operations becomes innumerably infinite. The term supertask was coined by the philosopher James F...
- What the Tortoise Said to AchillesWhat the Tortoise Said to Achilles"What the Tortoise Said to Achilles", written by Lewis Carroll in 1895 for the philosophical journal Mind, is a brief dialogue which problematises the foundations of logic. The title alludes to one of Zeno's paradoxes of motion, in which Achilles could never overtake the tortoise in a race...
- Zeno machineZeno machineIn mathematics and computer science, Zeno machines are a hypothetical computational model related to Turing machines that allows a countably infinite number of algorithmic steps to be performed in finite time...
External links
- Silagadze, Z . K. "Zeno meets modern science,"
- Zeno's Paradox: Achilles and the Tortoise by Jon McLoone, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Kevin Brown on Zeno and the Paradox of Motion

