
The Quadrature of the Parabola
Encyclopedia

The Quadrature of the Parabola is a treatise on geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, written by Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
in the 3rd century BC. Written as a letter to his friend Dositheus, the work presents 24 propositions regarding parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
s, culminating in a proof that the area of a parabolic segment (the region enclosed by a parabola and a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
) is 4/3 that of a certain inscribe
Inscribe
right|thumb|An inscribed triangle of a circleIn geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "Figure F is inscribed in figure G" means precisely the same thing as "figure G is circumscribed about...
d triangle.
The statement of the problem used the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
. Archimedes may have dissected the area into infinitely many triangles whose areas form a geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
. He computes the sum of the resulting geometric series, and proves that this is the area of the parabolic segment. This represents the most sophisticated use of the method of exhaustion in ancient mathematics, and remained unsurpassed until the development of integral calculus in the 17th century, being succeeded by Cavalieri's quadrature formula.
In 1906 Heiberg suggested that Archimedes' proof was written as
4A/3 = A + A/4 + A/12
Main theorem
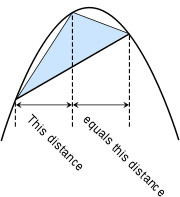
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
of the parabola, and the third vertex is the point of tangency such that the given tangent is parallel to the chord. From Proposition 1 (Quadrature of the Parabola), this means that a line from the third vertex, which is drawn parallel to the axis (or the axis itself), divides the chord into equal segments. The main theorem claims that the area of the parabolic segment is 4/3 that of the inscribed triangle.
Structure of the text
Archimedes gives two proofs of the main theorem. The first uses abstract mechanicsMechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, with Archimedes arguing that the weight of the segment will balance the weight of the triangle when placed on an appropriate lever
Lever
In physics, a lever is a rigid object that is used with an appropriate fulcrum or pivot point to either multiply the mechanical force that can be applied to another object or resistance force , or multiply the distance and speed at which the opposite end of the rigid object travels.This leverage...
. The second, more famous proof uses pure geometry, specifically the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
.
Of the twenty-four propositions, the first three are quoted without proof from Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's Elements of Conics (a lost work by Euclid on conic sections). Propositions four and five establish elementary properties of the parabola; propositions six through seventeen give the mechanical proof of the main theorem; and propositions eighteen through twenty-four present the geometric proof.
Dissection of the parabolic segment
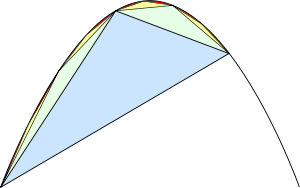
Areas of the triangles
In propositions eighteen through twenty-one, Archimedes proves that the area of each green triangle is one eighth of the area of the blue triangle. From a modern point of view, this is because the green triangle has half the width and a fourth of the height: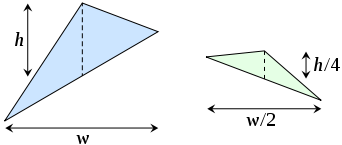
By extension, each of the yellow triangles has one eighth the area of a green triangle, each of the red triangles has one eighth the area of a yellow triangle, and so on. Using the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
, it follows that the total area of the parabolic segment is given by
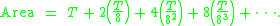
Here T represents the area of the large blue triangle, the second term represents the total area of the two green triangles, the third term represents the total area of the four yellow triangles, and so forth. This simplifies to give
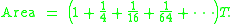
Sum of the series
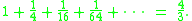
The expression on the left is a geometric series—each successive term is one fourth of the previous term. In modern mathematics, the formula above is a special case of the sum formula for a geometric series.
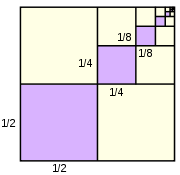
Archimedes evaluates the sum using an entirely geometric method, illustrated in the picture to the right. This picture shows a unit square which has been dissected into an infinity of smaller squares. Each successive purple square has one fourth the area of the previous square, with the total purple area being the sum
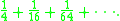
However, the purple squares are congruent to either set of yellow squares, and so cover 1/3 of the area of the unit square. It follows that the series above sums to 4/3.
See also
- ArchimedesArchimedesArchimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
- History of calculusHistory of calculusCalculus, historically known as infinitesimal calculus, is a mathematical discipline focused on limits, functions, derivatives, integrals, and infinite series. Ideas leading up to the notions of function, derivative, and integral were developed throughout the 17th century, but the decisive step was...
- Method of exhaustionMethod of exhaustionThe method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
- Geometric series

