Mathematical space - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a space is a set with some added structure

Mathematical structure

In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....

.

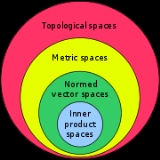
Mathematical spaces often form a hierarchy, i.e., one space may inherit all the characteristics of a parent space. For instance, all inner product space

Inner product space

In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

s are also normed vector space

Normed vector space

In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....

s, because the inner product induces a norm

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

on the inner product space such that:

Modern mathematics treats "space" quite differently compared to classical mathematics.

Before the golden age of geometry

In the ancient mathematics, "space" was a geometric abstraction of the
three-dimensional space observed in the everyday life. Axiomatic method had been the main research tool since Euclid

Euclid

Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...

(about 300 BC). The method of coordinates (analytic geometry

Analytic geometry

Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...

) was adopted by René Descartes

René Descartes

René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...

in 1637. At that time geometric theorems were treated as an absolute objective truth knowable through intuition and reason, similar to objects of natural science; and axioms were treated as obvious implications of definitions.

Two equivalence relations between geometric figures were used: congruence and similarity. Translations, rotations and reflections transform a figure into congruent figures; homotheties — into similar figures. For example, all circles are mutually similar, but ellipses are not similar to circles. A third equivalence relation, introduced by projective geometry

Projective geometry

In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...

(Gaspard Monge

Gaspard Monge

Gaspard Monge, Comte de Péluse was a French mathematician, revolutionary, and was inventor of descriptive geometry. During the French Revolution, he was involved in the complete reorganization of the educational system, founding the École Polytechnique...

, 1795), corresponds to projective transformations. Not only ellipses but also parabolas and hyperbolas turn into circles under appropriate projective transformations; they all are projectively equivalent figures.

The relation between the two geometries, Euclidean and projective, shows that mathematical objects are not given to us with their structure. Rather, each mathematical theory describes its objects by some of their properties, precisely those that are put as axioms at the foundations of the theory.

Distances and angles are never mentioned in the axioms of the projective geometry and therefore cannot appear in its theorems. The question "what is the sum of the three angles of a triangle" is meaningful in the Euclidean geometry but meaningless in the projective geometry.

A different situation appeared in the 19th century: in some geometries the sum of the three angles of a triangle is well-defined but different from the classical value (180 degrees). The non-Euclidean hyperbolic geometry, introduced by Nikolai Lobachevsky in 1829 and János Bolyai

János Bolyai

János Bolyai was a Hungarian mathematician, known for his work in non-Euclidean geometry.Bolyai was born in the Transylvanian town of Kolozsvár , then part of the Habsburg Empire , the son of Zsuzsanna Benkő and the well-known mathematician Farkas Bolyai.-Life:By the age of 13, he had mastered...

in 1832 (and Carl Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

in 1816, unpublished) stated that the sum depends on the triangle and is always less than 180 degrees. Eugenio Beltrami

Eugenio Beltrami

Eugenio Beltrami was an Italian mathematician notable for his work concerning differential geometry and mathematical physics...

in 1868 and Felix Klein

Felix Klein

Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...

in 1871 obtained Euclidean "models" of the non-Euclidean hyperbolic geometry, and thereby completely justified this theory.

This discovery forced the abandonment of the pretensions to the absolute truth of Euclidean geometry. It showed that axioms are not "obvious", nor "implications of definitions". Rather, they are hypotheses. To what extent do they correspond to an experimental reality? This important physical problem no longer has anything to do with mathematics. Even if a "geometry" does not correspond to an experimental reality, its theorems remain no less "mathematical truths".

A Euclidean model of a non-Euclidean geometry is a clever choice of some objects existing in Euclidean space and some relations between these objects that satisfy all axioms (therefore, all theorems) of the non-Euclidean geometry. These Euclidean objects and relations "play" the non-Euclidean geometry like contemporary actors playing an ancient performance. Relations between the actors only mimic relations between the characters in the play. Likewise, the chosen relations between the chosen objects of the Euclidean model only mimic the non-Euclidean relations. It shows that relations between objects are essential in mathematics, while the nature of the objects is not.

The golden age and afterwards: dramatic change

According to Nicolas Bourbaki

Nicolas Bourbaki

Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...

, the period between 1795 ("Geometrie descriptive" of Monge) and 1872 (the "Erlangen program

Erlangen program

An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...

me" of Klein) can be called the golden age of geometry. Analytic geometry made a great progress and succeeded in replacing theorems of classical geometry with computations via invariants of transformation groups. Since that time new theorems of classical geometry interest amateurs rather than professional mathematicians.

However, it does not mean that the heritage of the classical geometry was lost. According to Bourbaki,
"passed over in its role as an autonomous and living science, classical geometry is thus transfigured into a universal language of contemporary mathematics".

According to the famous inaugural lecture given by Bernhard Riemann

Bernhard Riemann

Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....

in 1854, every mathematical object parametrized by

real numbers may be treated as a point of the

-dimensional space of all such objects.
Nowadays mathematicians follow this idea routinely and find it extremely suggestive to use the terminology of classical geometry nearly everywhere.

In order to fully appreciate the generality of this approach one should note that mathematics is "a pure theory of forms, which has as its purpose, not the combination of quantities, or of their images, the numbers, but objects of thought" (Hermann Hankel

Hermann Hankel

Hermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....

, 1867).

Functions are important mathematical objects. Usually they form infinite-dimensional spaces, as noted already by Riemann
and elaborated in the 20 century by functional analysis.

An object parametrized by

complex numbers may be treated as a point of a complex

-dimensional space. However, the same object is also parametrized by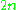

real numbers (real parts and imaginary parts of the complex numbers), thus, a point of a real

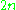-dimensional space. The complex dimension differs from the real dimension. This is only the tip of the iceberg. The "algebraic" concept of dimension applies to linear spaces. The "topological" concept of dimension applies to topological spaces. There is also Hausdorff dimension

Hausdorff dimension

thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...

for metric spaces; this one can be non-integer (especially for fractals). Some kinds of spaces (for instance, measure spaces) admit no concept of dimension at all.

The original space investigated by Euclid is now called "the three-dimensional Euclidean space". Its axiomatization, started by Euclid 23 centuries ago, was finalized in the 20 century by David Hilbert

David Hilbert

David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...

, Alfred Tarski

Alfred Tarski

Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...

and George Birkhoff

George David Birkhoff

-External links:* − from National Academies Press, by Oswald Veblen....

. This approach describes the space via undefined primitives (such as "point", "between", "congruent") constrained by a number of axioms. Such a definition "from scratch" is now of little use, since it does not reveal the relation of this space to other spaces. The modern approach defines the three-dimensional Euclidean space more algebraically, via linear spaces and quadratic forms, namely, as an affine space whose difference space is a three-dimensional inner product space.

Also a three-dimensional projective space is now defined non-classically, as the space of all one-dimensional subspaces (that is, straight lines through the origin) of a four-dimensional linear space.

A space consists now of selected mathematical objects (for instance, functions on another space, or subspaces of another space, or just elements of a set) treated as points, and selected relationships between these points. It shows that spaces are just mathematical structures. One may expect that the structures called "spaces" are more geometric than others, but this is not always true. For example, a differentiable manifold (called also smooth manifold) is much more geometric than a measurable space, but no one calls it "differentiable space" (nor "smooth space").

Three taxonomic ranks

Spaces are classified on three levels. Given that each mathematical theory describes its objects by some of their properties, the first question to ask is: which properties?

For example, the upper-level classification distinguishes between Euclidean and projective spaces, since the distance between two points is defined in Euclidean spaces but undefined in projective spaces. These are spaces of different type.

Another example. The question "what is the sum of the three angles of a triangle" makes sense in a Euclidean space but not in a projective space; these are spaces of different type. In a non-Euclidean space the question makes sense but is answered differently, which is not an upper-level distinction.

Also the distinction between a Euclidean plane and a Euclidean 3-dimensional space is not an upper-level distinction; the question "what is the dimension" makes sense in both cases.

In terms of Bourbaki
the upper-level classification is related to "typical characterization" (or "typification"). However, it is not the same (since two equivalent structures may differ in typification).

On the second level of classification one takes into account answers to especially important questions (among the questions that make sense according to the first level). For example, this level distinguishes between Euclidean and non-Euclidean spaces; between finite-dimensional and infinite-dimensional spaces; between compact and non-compact spaces, etc.

In terms of Bourbaki the second-level classification is the classification by "species". Unlike biological taxonomy, a space may belong to several species.

On the third level of classification, roughly speaking, one takes into account answers to all possible questions (that make sense according to the first level). For example, this level distinguishes between spaces of different dimension, but does not distinguish between a plane of a three-dimensional Euclidean space, treated as a two-dimensional Euclidean space, and the set of all pairs of real numbers, also treated as a two-dimensional Euclidean space. Likewise it does not distinguish between different Euclidean models of the same non-Euclidean space.

More formally, the third level classifies spaces up to isomorphism. An isomorphism between two spaces is defined as a one-to-one correspondence between the points of the first space and the points of the second space, that preserves all relations between the points, stipulated by the given "typification". Mutually isomorphic spaces are thought of as copies of a single space. If one of them belongs to a given species then they all do.

The notion of isomorphism sheds light on the upper-level classification. Given a one-to-one correspondence between two spaces of the same type, one may ask whether it is an isomorphism or not. This question makes no sense for two spaces of different type.

Isomorphisms to itself are called automorphisms. Automorphisms of a Euclidean space are motions and reflections. Euclidean space is homogeneous in the sense that every point can be transformed into every other point by some automorphism.

Two relations between spaces, and a property of spaces

Topological notions (continuity, convergence, open sets, closed sets etc.) are defined naturally in every Euclidean space. In other words, every Euclidean space is also a topological space. Every isomorphism between two Euclidean spaces is also an isomorphism between the corresponding topological spaces (called "homeomorphism

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

"), but the converse is wrong: a homeomorphism may distort distances. In terms of Bourbaki, "topological space" is an underlying structure of the "Euclidean space" structure. Similar ideas occur in category theory

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

: the category of Euclidean spaces is a concrete category over the category of topological spaces; the forgetful (or "stripping") functor maps the former category to the latter category.

A three-dimensional Euclidean space is a special case of a Euclidean space. In terms of Bourbaki, the species of three-dimensional Euclidean space is richer than the species of Euclidean space. Likewise, the species of compact topological space is richer than the species of topological space.

Euclidean axioms leave no freedom, they determine uniquely all geometric properties of the space. More exactly: all three-dimensional Euclidean spaces are mutually isomorphic. In this sense we have "the" three-dimensional Euclidean space. In terms of Bourbaki, the corresponding theory is univalent. In contrast, topological spaces are generally non-isomorphic, their theory is multivalent. A similar idea occurs in mathematical logic: a theory is called categorical if all its models of the same cardinality are mutually isomorphic. According to Bourbaki, the study of multivalent theories is the most striking feature which distinguishes modern mathematics from classical mathematics.

Linear and topological spaces

Two basic spaces are linear spaces (called also vector spaces) and topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

s.

Linear spaces are of algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

ic nature; there are real linear spaces (over the field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s),
complex linear spaces (over the field of complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s), and more generally, linear spaces over any field. Every complex linear space is also a real linear space (the latter underlies the former), since each real number is also a complex number.
For example, the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

treated as a one-dimensional complex linear space may be downgraded to a two-dimensional real linear space. In contrast, the real line

Real line

In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...

can be treated as a one-dimensional real linear space but not a complex linear space. See also Examples of vector spaces#Field extensions.
Linear operations, given in a linear space by definition, lead to such notions as straight lines (and planes, and other linear subspaces); parallel lines; ellipses (and ellipsoids). However, orthogonal (perpendicular) lines cannot be defined, and circles cannot be singled out among ellipses. The dimension of a linear space is defined as the maximal number of linearly independent

Linear independence

In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...

vectors or, equivalently, as the minimal number of vectors that span the space; it may be finite or infinite. Two linear spaces over the same field are isomorphic if and only if they are of the same dimension.

Topological spaces are of analytic

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

nature. Open set

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

s, given in a topological space by definition, lead to such notions as continuous function

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

s, paths, maps; convergent sequences, limits; interior, boundary, exterior. However, uniform continuity

Uniform continuity

In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...

, bounded set

Bounded set

In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...

s, Cauchy sequence

Cauchy sequence

In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...

s, differentiable function

Differentiable function

In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...

s (paths, maps) remain undefined. Isomorphism

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...

s between topological spaces are traditionally called homeomorphisms; these are one-to-one correspondences continuous in both directions. The open interval

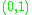is homeomorphic to the whole real line

Real line

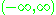but not homeomorphic to the closed interval

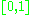, nor to a circle. The surface of a cube is homeomorphic to a sphere (the surface of a ball) but not homeomorphic to a torus. Euclidean spaces of different dimensions are not homeomorphic, which seems evident, but is not easy to prove. Dimension of a topological space is difficult to define; "inductive dimension" and "Lebesgue covering dimension" are used. Every subset of a topological space is itself a topological space (in contrast, only linear subsets of a linear space are linear spaces). Arbitrary topological spaces, investigated by general topology

General topology

In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...

(called also point-set topology) are too diverse for a complete classification (up to homeomorphism). They are inhomogeneous (in general). Compact topological spaces are an important class of topological spaces ("species" of this "type"). Every continuous function is bounded on such space. The closed interval

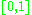and the extended real line

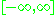are compact; the open interval

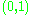and the line

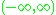are not. Geometric topology investigates manifolds (another "species" of this "type"); these are topological spaces locally homeomorphic to Euclidean spaces. Low-dimensional manifolds are completely classified (up to homeomorphism).

The two structures discussed above (linear and topological) are both underlying structures of the "linear topological space" structure. That is, a linear topological space is both a linear (real or complex) space and a (homogeneous, in fact) topological space. However, an arbitrary combination of these two structures is generally not a linear topological space; the two structures must conform, namely, the linear operations must be continuous.

Every finite-dimensional (real or complex) linear space is a linear topological space in the sense that it carries one and only one topology that makes it a linear topological space. The two structures, "finite-dimensional (real or complex) linear space" and "finite-dimensional linear topological space", are thus equivalent, that is, mutually underlying. Accordingly, every invertible linear transformation of a finite-dimensional linear topological space is a homeomorphism. In the infinite dimension, however, different topologies conform to a given linear structure, and invertible linear transformations are generally not homeomorphisms.

Affine and projective spaces

It is convenient to introduce affine

Affine space

In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...

and projective space

Projective space

In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....

s by means of linear spaces, as follows. An

-dimensional linear subspace of an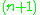

-dimensional linear space, being itself an

-dimensional linear space, is not homogeneous; it contains a special point, the origin. Shifting it by a vector external to it, one obtains an

-dimensional affine space. It is homogeneous. In the words of John Baez, "an affine space is a vector space that's forgotten its origin". A straight line in the affine space is, by definition, its intersection with a two-dimensional linear subspace (plane through the origin) of the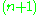

-dimensional linear space. Every linear space is also an affine space.

Every point of the affine space is its intersection with a one-dimensional linear subspace (line through the origin) of the

-dimensional linear space. However, some one-dimensional subspaces are parallel to the affine space; in some sense, they intersect it at infinity. The set of all one-dimensional linear subspaces of an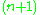

-dimensional linear space is, by definition, an

-dimensional projective space. Choosing an

-dimensional affine space as before one observes that the affine space is embedded as a proper subset into the projective space. However, the projective space itself is homogeneous. A straight line in the projective space, by definition, corresponds to a two-dimensional linear subspace of the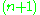

-dimensional linear space.

Defined this way, affine and projective spaces are of algebraic nature; they can be real, complex, and more generally, over any field.

Every real (or complex) affine or projective space is also a topological space. An affine space is a non-compact manifold; a projective space is a compact manifold.

Metric and uniform spaces

Distances between points are defined in a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

. Every metric space is also a topological space. Bounded sets and Cauchy sequences are defined in a metric space (but not just in a topological space). Isomorphisms between metric spaces are called isometries. A metric space is called complete if all Cauchy sequences converge. Every incomplete space is isometrically embedded into its completion. Every compact metric space is complete; the real line is non-compact but complete; the open interval

is incomplete.

A topological space is called metrizable, if it underlies a metric space. All manifolds are metrizable.

Every Euclidean space is also a complete metric space. Moreover, all geometric notions immanent to a Euclidean space can be characterized in terms of its metric. For example, the straight segment connecting two given points

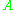and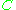

consists of all points

such that the distance between

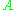and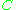

is equal to the sum of two distances, between

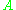and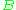

and between

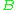and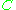

.

Uniform space

Uniform space

In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...

s do not introduce distances, but still allow one to use uniform continuity, Cauchy sequences, completeness and completion. Every uniform space is also a topological space. Every linear topological space (metrizable or not) is also a uniform space. More generally, every commutative topological group is also a uniform space. A non-commutative topological group, however, carries two uniform structures, one left-invariant, the other right-invariant. Linear topological spaces are complete in finite dimension but generally incomplete in infinite dimension.

Normed, Banach, inner product, and Hilbert spaces

Vectors in a Euclidean space are a linear space, but each vector

has also a length, in other words, norm,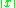

. A (real or complex) linear space endowed with a norm is a normed space. Every normed space is both a linear topological space and a metric space. A Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

is a complete normed space. Many spaces of sequences or functions are infinite-dimensional Banach spaces.

The set of all vectors of norm less than one is called the unit ball of a normed space. It is a convex, centrally symmetric set, generally not an ellipsoid; for example, it may be a polygon (on the plane). The parallelogram law (called also parallelogram identity)

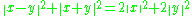generally fails in normed spaces, but holds for vectors in Euclidean spaces, which follows from the fact that the squared Euclidean norm of a vector is its inner product to itself.

An inner product space

Inner product space

is a (real or complex) linear space endowed with a bilinear (or sesquilinear) form satisfying some conditions and called inner product. Every inner product space is also a normed space. A normed space underlies an inner product space if and only if it satisfies the parallelogram law, or equivalently, if its unit ball is an ellipsoid. Angles between vectors are defined in inner product spaces. A Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

is defined as a complete inner product space. (Some authors insist that it must be complex, others admit also real Hilbert spaces.) Many spaces of sequences or functions are infinite-dimensional Hilbert spaces. Hilbert spaces are very important for quantum theory

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

.

All

-dimensional real inner product spaces are mutually isomorphic. One may say that the

-dimensional Euclidean space is the

-dimensional real inner product space that's forgotten its origin.

Smooth and Riemannian manifolds (spaces)

Smooth manifolds are not called "spaces", but could be. Smooth (differentiable) functions, paths, maps, given in a smooth manifold by definition, lead to tangent spaces. Every smooth manifold is a (topological) manifold. Smooth surfaces in a finite-dimensional linear space (like the surface of an ellipsoid, not a polytope) are smooth manifolds. Every smooth manifold can be embedded into a finite-dimensional linear space. A smooth path in a smooth manifold has (at every point) the tangent vector, belonging to the tangent space (attached to this point). Tangent spaces to an

-dimensional smooth manifold are

-dimensional linear spaces. A smooth function has (at every point) the differential, – a linear functional on the tangent space. Real (or complex) finite-dimensional linear, affine and projective spaces are also smooth manifolds.

A Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

, or Riemann space, is a smooth manifold whose tangent spaces are endowed with inner product (satisfying some conditions). Euclidean spaces are also Riemann spaces. Smooth surfaces in Euclidean spaces are Riemann spaces. A hyperbolic non-Euclidean space is also a Riemann space. A curve in a Riemann space has the length. A Riemann space is both a smooth manifold and a metric space; the length of the shortest curve is the distance. The angle between two curves intersecting at a point is the angle between their tangent lines.

Waiving positivity of inner product on tangent spaces one gets pseudo-Riemann (especially, Lorentzian) spaces very important for general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

Measurable, measure, and probability spaces

Waiving distances and angles while retaining volumes (of geometric bodies) one moves toward measure theory. Besides the volume, a measure generalizes area, length, mass (or charge) distribution, and also probability distribution, according to Andrei Kolmogorov's approach to probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

.

A "geometric body" of classical mathematics is much more regular than just a set of points. The boundary of the body is of zero volume. Thus, the volume of the body is the volume of its interior, and the interior can be exhausted by an infinite sequence of cubes. In contrast, the boundary of an arbitrary set of points can be of non-zero volume (an example: the set of all rational points inside a given cube). Measure theory succeeded in extending the notion of volume (or another measure) to a vast class of sets, so-called measurable sets. Indeed, non-measurable sets never occur in applications, but anyway, the theory must restrict itself to measurable sets (and functions).

Measurable sets, given in a measurable space by definition, lead to measurable functions and maps. In order to turn a topological space into a measurable space one endows it with a σ-algebra. The σ-algebra of Borel set

Borel set

In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...

s is most popular, but not the only choice (Baire set

Baire set

In mathematics, more specifically in measure theory, the notion of a Baire set is important in the understanding of particular relations between measure theory and topology. In particular, an understanding of Baire sets aids in intuition when one deals with measures on non-metrizable topological...

s, universally measurable set

Universally measurable set

In mathematics, a subset A of a Polish space X is universally measurable if it is measurable with respect to every complete probability measure on X that measures all Borel subsets of X. In particular, a universally measurable set of reals is necessarily Lebesgue measurable below.Every analytic...

s etc. are used sometimes). Alternatively, a σ-algebra can be generated by a given collection of sets (or functions) irrespective of any topology. Quite often, different topologies lead to the same σ-algebra (for example, the norm topology and the weak topology

Weak topology

In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...

on a separable Hilbert space). Every subset of a measurable space is itself a measurable space.

Standard measurable spaces (called also standard Borel spaces) are especially useful. Every Borel set (in particular, every closed set and every open set) in a Euclidean space (and more generally, in a complete separable metric space) is a standard measurable space. All uncountable standard measurable spaces are mutually isomorphic.

A measure space is a measurable space endowed with a measure. A Euclidean space with Lebesgue measure is a measure space. Integration theory defines integrability and integrals of measurable functions on a measure space.

Sets of measure 0, called null sets, are negligible. Accordingly, a

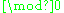isomorphism is defined as isomorphism between subsets of full measure (that is, with negligible complement).

A probability space

Probability space

In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...

is a measure space such that the measure of the whole space is equal to 1. The product of any family (finite or not) of probability spaces is a probability space. In contrast, for measure spaces in general, only the product of finitely many spaces is defined. Accordingly, there are many infinite-dimensional probability measures (especially, Gaussian measure

Gaussian measure

In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...

s), but no infinite-dimensional Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

.

Standard probability space

Standard probability space

In probability theory, a standard probability space is a probability space satisfying certain assumptions introduced by Vladimir Rokhlin in 1940...

s are especially useful. Every probability measure on a standard measurable space leads to a standard probability space. The product of a sequence (finite or not) of standard probability spaces is a standard probability space. All non-atomic standard probability spaces are mutually isomorphic

one of them is the interval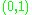

with Lebesgue measure.

These spaces are less geometric. In particular, the idea of dimension, applicable (in one form or another) to all other spaces, does not apply to measurable, measure and probability spaces.