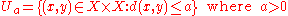Uniform space
Encyclopedia
In the mathematical field of topology
, a uniform space is a set with a uniform structure. Uniform spaces are topological space
s with additional structure which is used to define uniform properties
such as completeness
, uniform continuity
and uniform convergence.
The conceptual difference between uniform and topological structures is that in a uniform space, one can formalize certain notions of relative closeness and closeness of points. In other words, ideas like "x is closer to a than y is to b" make sense in uniform spaces. By comparison, in a general topological space, given sets A,B it is meaningful to say that a point x is arbitrarily close to A (i.e., in the closure of A), or perhaps that A is a smaller neighborhood of x than B, but notions of closeness of points and relative closeness are not described well by topological structure alone.
Uniform spaces generalize metric space
s and topological group
s and therefore underlie most of analysis
.
X × X (Φ is called the uniform structure or uniformity of X and its elements entourages (French
: neighborhoods or surroundings)) that satisfies the following axioms:
If the last property is omitted we call the space quasiuniform.
One usually writes U[x]={y : (x,y)∈U}. On a graph, a typical entourage is drawn as a blob surrounding the "y=x" diagonal; the U[x]’s are then the vertical cross-sections. If (x,y) ∈ U, one says that x and y are U-close. Similarly, if all pairs of points in a subset A of X are U-close (i.e., if A × A is contained in U), A is called U-small. An entourage U is symmetric if (x,y) ∈ U precisely when (y,x) ∈ U. The first axiom states that each point is U-close to itself for each entourage U. The third axiom guarantees that being "both U-close and V-close" is also a closeness relation in the uniformity. The fourth axiom states that for each entourage U there is an entourage V which is "half as large". Finally, the last axiom states the essentially symmetric property "closeness" with respect to a uniform structure.
A fundamental system of entourages of a uniformity Φ is any set B of entourages of Φ such that every entourage of Ф contains a set belonging to B. Thus, by property 2 above, a fundamental systems of entourages B is enough to specify the uniformity Φ unambiguously: Φ is the set of subsets of X × X that contain a set of B. Every uniform space has a fundamental system of entourages consisting of symmetric entourages.
The right intuition about uniformities is provided by the example of metric space
s: if (X,d) is a metric space, the sets
form a fundamental system of entourages for the standard uniform structure of X. Then x and y are Ua-close precisely when the distance between x and y is at most a.
A uniformity Φ is finer than another uniformity Ψ on the same set if Φ ⊇ Ψ; in that case Ψ is said to be coarser than Φ.
, an approach which is particularly useful in functional analysis
(with pseudometrics provided by seminorms). More precisely, let f: X × X → R be a pseudometric on a set X. The inverse images Ua = f –1([0,a]) for a > 0 can be shown to form a fundamental system of entourages of a uniformity. The uniformity generated by the Ua is the uniformity defined by the single pseudometric f. Certain authors call spaces the topology of which is defined in terms of pseudometrics gauge spaces.
For a family (fi) of pseudometrics on X, the uniform structure defined by the family is the least upper bound of the uniform structures defined by the individual pseudometrics fi. A fundamental system of entourages of this uniformity is provided by the set of finite intersections of entourages of the uniformities defined by the individual pseudometrics fi. If the family of pseudometrics is finite, it can be seen that the same uniform structure is defined by a single pseudometric, namely the upper envelope sup fi of the family.
Less trivially, it can be shown that a uniform structure that admits a countable fundamental system of entourages (and hence in particular a uniformity defined by a countable family of pseudometrics) can be defined by a single pseudometric. A consequence is that any uniform structure can be defined as above by a (possibly uncountable) family of pseudometrics (see Bourbaki: General Topology Chapter IX §1 no. 4).
of X, forming a filter
when ordered by star refinement. One says cover P is a star refinement
of cover Q, written P <* Q, if for every A ∈ P, there is a U ∈ Q such that if A ∩ B ≠ ø, B ∈ P, then B ⊆ U. Axiomatically, this reduces to:
Given a point x and a uniform cover P, one can consider the union of the members of P that contain x as a typical neighbourhood of x of "size" P, and this intuitive measure applies uniformly over the space.
Given a uniform space in the entourage sense, define a cover P to be uniform if there is some entourage U such that for each x ∈ X, there is an A ∈ P such that U[x] ⊆ A. These uniform covers form a uniform space as in the second definition. Conversely, given a uniform space in the uniform cover sense, the supersets of ⋃{A × A : A ∈ P}, as P ranges over the uniform covers, are the entourages for a uniform space as in the first definition. Moreover, these two transformations are inverses of each other.
by defining a subset O of X to be open if and only if for every x in O there exists an entourage V such that V[x] is a subset of O. In this topology, the neighbourhood filter of a point x is {V[x] : V∈Φ}. This can be proved with a recursive use of the existence of a "half-size" entourage. Compared to a general topological space the existence of the uniform structure makes possible the comparison of sizes of neighbourhoods: V[x] and V[y] are considered to be of the "same size".
The topology defined by a uniform structure is said to be induced by the uniformity. A uniform structure on a topological space is compatible with the topology if the topology defined by the uniform structure coincides with the original topology. In general several different uniform structures can be compatible with a given topology on X.
Every uniformizable space is a completely regular topological space. Moreover, for a uniformizable space X the following are equivalent:
The topology of a uniformizable space is always a symmetric topology; that is, the space is an R0-space.
Conversely, each completely regular space is uniformizable. A uniformity compatible with the topology of a completely regular space X can be defined as the coarsest uniformity which makes all continuous real-valued functions on X uniformly continuous. A fundamental system of entourages for this uniformity is provided by all finite intersections of sets (f × f)-1(V),
where f is a continuous real-valued function on X and V is an entourage of the uniform space R. This uniformity defines a topology, which is clearly coarser than the original topology of X; that it is also finer than the original topology (hence coincides with it) is a simple consequence of complete regularity: for any x ∈ X and a neighbourhood V of x, there is a continuous real-valued function f with f(x)=0 and equal to 1 in the complement of V.
In particular, a compact Hausdorff space is uniformizable. In fact, for a compact Hausdorff space X the set of all neighbourhoods of the diagonal in X × X form the unique uniformity compatible with the topology.
A Hausdorff uniform space is metrizable if its uniformity can be defined by a countable family of pseudometrics. Indeed, as discussed above, such a uniformity can be defined by a single pseudometric, which is necessarily a metric if the space is Hausdorff. In particular, if the topology of a vector space
is Hausdorff and definable by a countable family of seminorms, it is metrizable.
s between topological space
s, which preserve topological properties, are the uniform continuous functions between uniform spaces, which preserve uniform properties. Uniform spaces with uniform maps form a category
. An isomorphism
between uniform spaces is called a uniform isomorphism
.
A uniformly continuous function is defined as one where inverse images of entourages are again entourages, or equivalently, one where the inverse images of uniform covers are again uniform covers.
All uniformly continuous functions are continuous with respect to the induced topologies.
s, one works with Cauchy filters (or Cauchy net
s).
A Cauchy filter F on a uniform space X is a filter
F such that for every entourage U, there exists A∈F with A×A ⊆ U. In other words, a filter is Cauchy if it contains "arbitrarily small" sets. It follows from the definitions that each filter that converges (with respect to the topology defined by the uniform structure) is a Cauchy filter.
A Cauchy filter is called minimal if it contains no smaller (i.e., coarser) Cauchy filter (other than itself). It can be shown that every Cauchy filter contains a unique minimal Cauchy filter. The neighbourhood filter of each point (the filter consisting of all neighbourhoods of the point) is a minimal Cauchy filter.
Conversely, a uniform space is called complete if every Cauchy filter converges. Any compact Hausdorff space is a complete uniform space with respect to the unique uniformity compatible with the topology.
Complete uniform space enjoy the following important property: if f: A → Y is a uniformly continuous function from a dense subset A of a uniform space X into a complete uniform space Y, then f can be extended (uniquely) into a uniformly continuous function on all of X.
A topological space which can be made into a complete uniform space, whose uniformity induces the original topology, is called a completely uniformizable space
.
The Hausdorff completion Y is unique up to isomorphism. As a set, Y can be taken to consist of the minimal Cauchy filters on X. As the neighbourhood filter B(x) of each point x in X is a minimal Cauchy filter, the map i can be defined by mapping x to B(x). The map i thus defined is in general not injective; in fact, the graph of the equivalence relation i(x) = i(x ') is the intersection of all entourages of X, and thus i is injective precisely when X is Hausdorff.
The uniform structure on Y is defined as follows: for each symmetric entourage V (i.e., such that (x,y) is in V precisely when (y,x) is in V), let C(V) be the set of all pairs (F,G) of minimal Cauchy filters which have in common at least one V-small set. The sets C(V) can be shown to form a fundamental system of entourages; Y is equipped with the uniform structure thus defined.
The set i(X) is then a dense subset of Y. If X is Hausdorff, then i is an isomorphism onto i(X), and thus X can be identified with a dense subset of its completion. Moreover, i(X) is always Hausdorff; it is called the Hausdorff uniform space associated with X. If R denotes the equivalence relation i(x) = i(x '), then the quotient space X/R is homeomorphic to i(X).
gave the first explicit definition of a uniform structure in 1937, uniform concepts, like completeness, were discussed using metric spaces. Nicolas Bourbaki
provided the definition of uniform structure in terms of entourages in the book Topologie Générale and John Tukey
gave the uniform cover definition. Weil also characterized uniform spaces in terms of a family of pseudometrics.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a uniform space is a set with a uniform structure. Uniform spaces are topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s with additional structure which is used to define uniform properties
Uniform property
In the mathematical field of topology a uniform property or uniform invariant is a property of a uniform space which is invariant under uniform isomorphisms....
such as completeness
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
, uniform continuity
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
and uniform convergence.
The conceptual difference between uniform and topological structures is that in a uniform space, one can formalize certain notions of relative closeness and closeness of points. In other words, ideas like "x is closer to a than y is to b" make sense in uniform spaces. By comparison, in a general topological space, given sets A,B it is meaningful to say that a point x is arbitrarily close to A (i.e., in the closure of A), or perhaps that A is a smaller neighborhood of x than B, but notions of closeness of points and relative closeness are not described well by topological structure alone.
Uniform spaces generalize metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s and topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s and therefore underlie most of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
Entourage definition
A uniform space (X, Φ) is a set X equipped with a nonempty family Φ of subsets of the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
X × X (Φ is called the uniform structure or uniformity of X and its elements entourages (French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
: neighborhoods or surroundings)) that satisfies the following axioms:
- if U is in Φ, then U contains the diagonal Δ = { (x, x) : x ∈ X }.
- if U is in Φ and V is a subset of X × X which contains U, then V is in Φ
- if U and V are in Φ, then U ∩ V is in Φ
- if U is in Φ, then there exists V in Φ such that, whenever (x, y) and (y, z) are in V, then (x, z) is in U.
- if U is in Φ, then U-1 = { (y, x) : (x, y) in U } is also in Φ
If the last property is omitted we call the space quasiuniform.
One usually writes U[x]={y : (x,y)∈U}. On a graph, a typical entourage is drawn as a blob surrounding the "y=x" diagonal; the U[x]’s are then the vertical cross-sections. If (x,y) ∈ U, one says that x and y are U-close. Similarly, if all pairs of points in a subset A of X are U-close (i.e., if A × A is contained in U), A is called U-small. An entourage U is symmetric if (x,y) ∈ U precisely when (y,x) ∈ U. The first axiom states that each point is U-close to itself for each entourage U. The third axiom guarantees that being "both U-close and V-close" is also a closeness relation in the uniformity. The fourth axiom states that for each entourage U there is an entourage V which is "half as large". Finally, the last axiom states the essentially symmetric property "closeness" with respect to a uniform structure.
A fundamental system of entourages of a uniformity Φ is any set B of entourages of Φ such that every entourage of Ф contains a set belonging to B. Thus, by property 2 above, a fundamental systems of entourages B is enough to specify the uniformity Φ unambiguously: Φ is the set of subsets of X × X that contain a set of B. Every uniform space has a fundamental system of entourages consisting of symmetric entourages.
The right intuition about uniformities is provided by the example of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s: if (X,d) is a metric space, the sets
form a fundamental system of entourages for the standard uniform structure of X. Then x and y are Ua-close precisely when the distance between x and y is at most a.
A uniformity Φ is finer than another uniformity Ψ on the same set if Φ ⊇ Ψ; in that case Ψ is said to be coarser than Φ.
Pseudometrics definition
Uniform spaces may be defined alternatively and equivalently using systems of pseudometricsPseudometric space
In mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
, an approach which is particularly useful in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
(with pseudometrics provided by seminorms). More precisely, let f: X × X → R be a pseudometric on a set X. The inverse images Ua = f –1([0,a]) for a > 0 can be shown to form a fundamental system of entourages of a uniformity. The uniformity generated by the Ua is the uniformity defined by the single pseudometric f. Certain authors call spaces the topology of which is defined in terms of pseudometrics gauge spaces.
For a family (fi) of pseudometrics on X, the uniform structure defined by the family is the least upper bound of the uniform structures defined by the individual pseudometrics fi. A fundamental system of entourages of this uniformity is provided by the set of finite intersections of entourages of the uniformities defined by the individual pseudometrics fi. If the family of pseudometrics is finite, it can be seen that the same uniform structure is defined by a single pseudometric, namely the upper envelope sup fi of the family.
Less trivially, it can be shown that a uniform structure that admits a countable fundamental system of entourages (and hence in particular a uniformity defined by a countable family of pseudometrics) can be defined by a single pseudometric. A consequence is that any uniform structure can be defined as above by a (possibly uncountable) family of pseudometrics (see Bourbaki: General Topology Chapter IX §1 no. 4).
Uniform cover definition
A uniform space (X,Θ) is a set X equipped with a distinguished family of uniform covers Θ from the set of coveringsCover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
of X, forming a filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
when ordered by star refinement. One says cover P is a star refinement
Star refinement
In mathematics, specifically in the study of topology and open covers of a topological space X, a star refinement is a particular kind of refinement of an open cover of X....
of cover Q, written P <* Q, if for every A ∈ P, there is a U ∈ Q such that if A ∩ B ≠ ø, B ∈ P, then B ⊆ U. Axiomatically, this reduces to:
- {X} is a uniform cover.
- If P <* Q and P is a uniform cover, then Q is also a uniform cover.
- If P and Q are uniform covers, then there is a uniform cover R that star-refines both P and Q.
Given a point x and a uniform cover P, one can consider the union of the members of P that contain x as a typical neighbourhood of x of "size" P, and this intuitive measure applies uniformly over the space.
Given a uniform space in the entourage sense, define a cover P to be uniform if there is some entourage U such that for each x ∈ X, there is an A ∈ P such that U[x] ⊆ A. These uniform covers form a uniform space as in the second definition. Conversely, given a uniform space in the uniform cover sense, the supersets of ⋃{A × A : A ∈ P}, as P ranges over the uniform covers, are the entourages for a uniform space as in the first definition. Moreover, these two transformations are inverses of each other.
Topology of uniform spaces
Every uniform space X becomes a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
by defining a subset O of X to be open if and only if for every x in O there exists an entourage V such that V[x] is a subset of O. In this topology, the neighbourhood filter of a point x is {V[x] : V∈Φ}. This can be proved with a recursive use of the existence of a "half-size" entourage. Compared to a general topological space the existence of the uniform structure makes possible the comparison of sizes of neighbourhoods: V[x] and V[y] are considered to be of the "same size".
The topology defined by a uniform structure is said to be induced by the uniformity. A uniform structure on a topological space is compatible with the topology if the topology defined by the uniform structure coincides with the original topology. In general several different uniform structures can be compatible with a given topology on X.
Uniformizable spaces
A topological space is called uniformizable if there is a uniform structure compatible with the topology.Every uniformizable space is a completely regular topological space. Moreover, for a uniformizable space X the following are equivalent:
- X is a Kolmogorov spaceKolmogorov spaceIn topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
- X is a Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
- X is a Tychonoff spaceTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
- for any compatible uniform structure, the intersection of all entourages is the diagonal {(x, x) : x in X}.
The topology of a uniformizable space is always a symmetric topology; that is, the space is an R0-space.
Conversely, each completely regular space is uniformizable. A uniformity compatible with the topology of a completely regular space X can be defined as the coarsest uniformity which makes all continuous real-valued functions on X uniformly continuous. A fundamental system of entourages for this uniformity is provided by all finite intersections of sets (f × f)-1(V),
where f is a continuous real-valued function on X and V is an entourage of the uniform space R. This uniformity defines a topology, which is clearly coarser than the original topology of X; that it is also finer than the original topology (hence coincides with it) is a simple consequence of complete regularity: for any x ∈ X and a neighbourhood V of x, there is a continuous real-valued function f with f(x)=0 and equal to 1 in the complement of V.
In particular, a compact Hausdorff space is uniformizable. In fact, for a compact Hausdorff space X the set of all neighbourhoods of the diagonal in X × X form the unique uniformity compatible with the topology.
A Hausdorff uniform space is metrizable if its uniformity can be defined by a countable family of pseudometrics. Indeed, as discussed above, such a uniformity can be defined by a single pseudometric, which is necessarily a metric if the space is Hausdorff. In particular, if the topology of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
is Hausdorff and definable by a countable family of seminorms, it is metrizable.
Uniform continuity
Similar to continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s between topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, which preserve topological properties, are the uniform continuous functions between uniform spaces, which preserve uniform properties. Uniform spaces with uniform maps form a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
. An isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between uniform spaces is called a uniform isomorphism
Uniform isomorphism
In the mathematical field of topology a uniform isomorphism or uniform homeomorphism is a special isomorphism between uniform spaces which respects uniform properties.-Definition:...
.
A uniformly continuous function is defined as one where inverse images of entourages are again entourages, or equivalently, one where the inverse images of uniform covers are again uniform covers.
All uniformly continuous functions are continuous with respect to the induced topologies.
Completeness
Generalising the notion of complete metric space, one can also define completeness for uniform spaces. Instead of working with Cauchy sequenceCauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s, one works with Cauchy filters (or Cauchy net
Cauchy net
In mathematics, a Cauchy net generalizes the notion of Cauchy sequence to nets defined on uniform spaces.A net is a Cauchy net if for every entourage V there exists γ such that for all α, β ≥ γ, is a member of V. More generally, in a Cauchy space, a net is Cauchy if the filter generated by the...
s).
A Cauchy filter F on a uniform space X is a filter
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
F such that for every entourage U, there exists A∈F with A×A ⊆ U. In other words, a filter is Cauchy if it contains "arbitrarily small" sets. It follows from the definitions that each filter that converges (with respect to the topology defined by the uniform structure) is a Cauchy filter.
A Cauchy filter is called minimal if it contains no smaller (i.e., coarser) Cauchy filter (other than itself). It can be shown that every Cauchy filter contains a unique minimal Cauchy filter. The neighbourhood filter of each point (the filter consisting of all neighbourhoods of the point) is a minimal Cauchy filter.
Conversely, a uniform space is called complete if every Cauchy filter converges. Any compact Hausdorff space is a complete uniform space with respect to the unique uniformity compatible with the topology.
Complete uniform space enjoy the following important property: if f: A → Y is a uniformly continuous function from a dense subset A of a uniform space X into a complete uniform space Y, then f can be extended (uniquely) into a uniformly continuous function on all of X.
A topological space which can be made into a complete uniform space, whose uniformity induces the original topology, is called a completely uniformizable space
Completely uniformizable space
In mathematics, a topological space is called completely uniformizable if there exists at least one complete uniformity that induces the topology T...
.
Hausdorff completion of a uniform space
As with metric spaces, every uniform space X has a Hausdorff completion: that is, there exists a complete Hausdorff uniform space Y and a uniformly continuous map i: X → Y with the following property:- for any uniformly continuous mapping f of X into a complete Hausdorff uniform space Z, there is a unique uniformly continuous map g: Y → Z such that f = gi.
The Hausdorff completion Y is unique up to isomorphism. As a set, Y can be taken to consist of the minimal Cauchy filters on X. As the neighbourhood filter B(x) of each point x in X is a minimal Cauchy filter, the map i can be defined by mapping x to B(x). The map i thus defined is in general not injective; in fact, the graph of the equivalence relation i(x) = i(x ') is the intersection of all entourages of X, and thus i is injective precisely when X is Hausdorff.
The uniform structure on Y is defined as follows: for each symmetric entourage V (i.e., such that (x,y) is in V precisely when (y,x) is in V), let C(V) be the set of all pairs (F,G) of minimal Cauchy filters which have in common at least one V-small set. The sets C(V) can be shown to form a fundamental system of entourages; Y is equipped with the uniform structure thus defined.
The set i(X) is then a dense subset of Y. If X is Hausdorff, then i is an isomorphism onto i(X), and thus X can be identified with a dense subset of its completion. Moreover, i(X) is always Hausdorff; it is called the Hausdorff uniform space associated with X. If R denotes the equivalence relation i(x) = i(x '), then the quotient space X/R is homeomorphic to i(X).
Examples
- Every metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(M, d) can be considered as a uniform space. Indeed, since a metric is a fortiori a pseudometric, the pseudometric definition furnishes M with a uniform structure. A fundamental system of entourages of this uniformity is provided by the sets
This uniform structure on M generates the usual metric space topology on M. However, different metric spaces can have the same uniform structure (trivial example is provided by a constant multiple of a metric). This uniform structure produces also equivalent definitions of uniform continuity Uniform continuityIn mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
Uniform continuityIn mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
and completeness for metric spaces. - Using metrics, a simple example of distinct uniform structures with coinciding topologies can be constructed. For instance, let d1(x,y) = | x − y | be the usual metric on R and let d2(x,y) = | ex − ey |. Then both metrics induce the usual topology on R, yet the uniform structures are distinct, since { (x,y) : | x − y | < 1 } is an entourage in the uniform structure for d1 but not for d2. Informally, this example can be seen as taking the usual uniformity and distorting it through the action of a continuous yet non-uniformly continuous function.
- Every topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
G (in particular, every topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
) becomes a uniform space if we define a subset V of G × G to be an entourage if and only if it contains the set { (x, y) : x⋅y−1 in U } for some neighborhood U of the identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of G. This uniform structure on G is called the right uniformity on G, because for every a in G, the right multiplication x → x⋅a is uniformly continuous with respect to this uniform structure. One may also define a left uniformity on G; the two need not coincide, but they both generate the given topology on G.
History
Before André WeilAndré Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
gave the first explicit definition of a uniform structure in 1937, uniform concepts, like completeness, were discussed using metric spaces. Nicolas Bourbaki
Nicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
provided the definition of uniform structure in terms of entourages in the book Topologie Générale and John Tukey
John Tukey
John Wilder Tukey ForMemRS was an American statistician.- Biography :Tukey was born in New Bedford, Massachusetts in 1915, and obtained a B.A. in 1936 and M.Sc. in 1937, in chemistry, from Brown University, before moving to Princeton University where he received a Ph.D...
gave the uniform cover definition. Weil also characterized uniform spaces in terms of a family of pseudometrics.
See also
- Uniform isomorphismUniform isomorphismIn the mathematical field of topology a uniform isomorphism or uniform homeomorphism is a special isomorphism between uniform spaces which respects uniform properties.-Definition:...
- Uniform propertyUniform propertyIn the mathematical field of topology a uniform property or uniform invariant is a property of a uniform space which is invariant under uniform isomorphisms....
- Uniformly connected spaceUniformly connected spaceIn topology and related areas of mathematics a uniformly connected space or Cantor connected space is a uniform space U such that every uniformly continuous function from U to a discrete uniform space is constant....
- Completely uniformizable spaceCompletely uniformizable spaceIn mathematics, a topological space is called completely uniformizable if there exists at least one complete uniformity that induces the topology T...
- Complete metric space
- Uniform continuityUniform continuityIn mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
- Space (mathematics)