Linear independence
Encyclopedia
In linear algebra
, a family of vector
s is linearly independent if none of them can be written as a linear combination
of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent. For instance, in the three-dimensional real vector space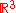
we have the following example.
Here the first three vectors are linearly independent; but the fourth vector equals 9 times the first plus 5 times the second plus 4 times the third, so the four vectors together are linearly dependent. Linear dependence is a property of the family, not of any particular vector; for example in this case we could just as well write the first vector as a linear combination of the last three.
In probability theory
and statistics
there is an unrelated measure of linear dependence between random variable
s.
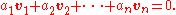
Note that the zero on the right is the zero vector, not the number zero.
If such scalars do not exist, then the vectors are said to be linearly independent.
Alternatively, linear independence can be directly defined as follows: a set of vectors is linearly independent if and only if the only representations of the zero vector as linear combinations of its elements are trivial solution
solutions i.e. whenever a1, a2, ..., an are scalars such that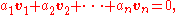
if and only if ai = 0 for i = 1, 2, ..., n.
A set of vectors is then said to be linearly dependent if it is not linearly independent.
More generally, let V be a vector space over a field
K, and let {vi | i∈I} be a family of elements of V. The family is linearly dependent over K if there exists a family {aj | j∈J} of elements of K, not all zero, such that
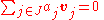
where the index set J is a nonempty, finite subset of I.
A set X of elements of V is linearly independent if the corresponding family {x}x∈X is linearly independent.
Equivalently, a family is dependent if a member is in the linear span
of the rest of the family, i.e., a member is a linear combination
of the rest of the family.
A set of vectors which is linearly independent and spans
some vector space, forms a basis
for that vector space. For example, the vector space of all polynomials in x over the reals has for a basis the (infinite) subset {1, x, x2, ...}.
In this example the "5 miles north" vector and the "6 miles east" vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third "7.81 miles northeast" vector is a linear combination
of the other two vectors, and it makes the set of vectors linearly dependent, that is, one of the three vectors is unnecessary.
Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, n linearly independent vectors are required to describe any location in n-dimensional space.
are linearly independent.
s such that
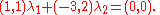
Taking each coordinate alone, this means
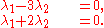
Solving for λ1 and λ2, we find that λ1 = 0 and λ2 = 0.
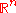are linearly dependent if and only if
the determinant
of the matrix
formed by taking the vectors as its columns is zero.
In this case, the matrix formed by the vectors is
We may write a linear combination of the columns as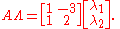
We are interested in whether AΛ = 0 for some nonzero vector Λ. This depends on the determinant of A, which is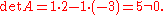
Since the determinant
is non-zero, the vectors (1, 1) and (−3, 2) are linearly independent.
Otherwise, suppose we have m vectors of n coordinates, with m < n. Then A is an n×m matrix and Λ is a column vector with m entries, and we are again interested in AΛ = 0. As we saw previously, this is equivalent to a list of n equations. Consider the first m rows of A, the first m equations; any solution of the full list of equations must also be true of the reduced list. In fact, if 〈i1,...,im〉 is any list of m rows, then the equation must be true for those rows.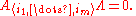
Furthermore, the reverse is true. That is, we can test whether the m vectors are linearly dependent by testing whether
for all possible lists of m rows. (In case m = n, this requires only one determinant, as above. If m > n, then it is a theorem that the vectors must be linearly dependent.) This fact is valuable for theory; in practical calculations more efficient methods are available.
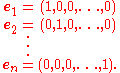
Then e1, e2, ..., en are linearly independent.
Since
then ai = 0 for all i in {1, ..., n}.
of all function
s of a real variable t. Then the functions et and e2t in V are linearly independent.
for all values of t. We need to show that a = 0 and b = 0. In order to do this, we divide through by et (which is never zero) and subtract to obtain
In other words, the function bet must be independent of t, which only occurs when b = 0. It follows that a is also zero.
, 
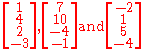
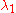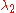and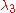 
such that
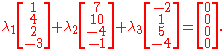
Forming the simultaneous equations:
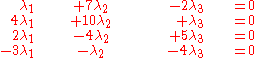
we can solve (using, for example, Gaussian elimination
) to obtain: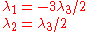
where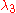
can be chosen arbitrarily.
Since these are nontrivial results, the vectors are linearly dependent.
(a1, ..., an) with n scalar
components, not all zero, such that
If such a linear dependence exists, then the n vectors are linearly dependent. It makes sense to identify two linear dependences if one arises as a non-zero multiple of the other, because in this case the two describe the same linear relationship among the vectors. Under this identification, the set of all linear dependences among v1, ...., vn is a projective space
.
is sometimes called a measure of "linear dependence" between two random variable
s. That does not mean the same thing as in the context of linear algebra
. When the covariance is normalized, one obtains the correlation matrix. From it, one can obtain the Pearson coefficient, which gives us the goodness of the fit for the best possible linear function
describing the relation between the variables. In this sense covariance is a linear gauge of dependence.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a family of vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s is linearly independent if none of them can be written as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent. For instance, in the three-dimensional real vector space
we have the following example.Here the first three vectors are linearly independent; but the fourth vector equals 9 times the first plus 5 times the second plus 4 times the third, so the four vectors together are linearly dependent. Linear dependence is a property of the family, not of any particular vector; for example in this case we could just as well write the first vector as a linear combination of the last three.
In probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
there is an unrelated measure of linear dependence between random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s.
Definition
A finite subset of n vectors, v1, v2, ..., vn, from the vector space V, is linearly dependent if and only if there exists a set of n scalars, a1, a2, ..., an, not all zero, such that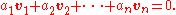Note that the zero on the right is the zero vector, not the number zero.
If such scalars do not exist, then the vectors are said to be linearly independent.
Alternatively, linear independence can be directly defined as follows: a set of vectors is linearly independent if and only if the only representations of the zero vector as linear combinations of its elements are trivial solution
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
solutions i.e. whenever a1, a2, ..., an are scalars such that
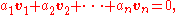
if and only if ai = 0 for i = 1, 2, ..., n.
A set of vectors is then said to be linearly dependent if it is not linearly independent.
More generally, let V be a vector space over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, and let {vi | i∈I} be a family of elements of V. The family is linearly dependent over K if there exists a family {aj | j∈J} of elements of K, not all zero, such that
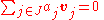
where the index set J is a nonempty, finite subset of I.
A set X of elements of V is linearly independent if the corresponding family {x}x∈X is linearly independent.
Equivalently, a family is dependent if a member is in the linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of the rest of the family, i.e., a member is a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the rest of the family.
A set of vectors which is linearly independent and spans
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
some vector space, forms a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for that vector space. For example, the vector space of all polynomials in x over the reals has for a basis the (infinite) subset {1, x, x2, ...}.
Geometric meaning
A geographic example may help to clarify the concept of linear independence. A person describing the location of a certain place might say, "It is 5 miles north and 6 miles east of here." This is sufficient information to describe the location, because the geographic coordinate system may be considered as a 2-dimensional vector space (ignoring altitude). The person might add, "The place is 7.81 miles northeast of here." Although this last statement is true, it is not necessary.In this example the "5 miles north" vector and the "6 miles east" vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third "7.81 miles northeast" vector is a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the other two vectors, and it makes the set of vectors linearly dependent, that is, one of the three vectors is unnecessary.
Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, n linearly independent vectors are required to describe any location in n-dimensional space.
Example I
The vectors (1, 1) and (−3, 2) in are linearly independent.Proof
Let λ1 and λ2 be two real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s such that
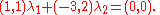
Taking each coordinate alone, this means
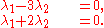
Solving for λ1 and λ2, we find that λ1 = 0 and λ2 = 0.
Alternative method using determinants
An alternative method uses the fact that n vectors in are linearly dependent if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
formed by taking the vectors as its columns is zero.
In this case, the matrix formed by the vectors is
We may write a linear combination of the columns as
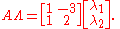
We are interested in whether AΛ = 0 for some nonzero vector Λ. This depends on the determinant of A, which is
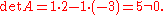
Since the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is non-zero, the vectors (1, 1) and (−3, 2) are linearly independent.
Otherwise, suppose we have m vectors of n coordinates, with m < n. Then A is an n×m matrix and Λ is a column vector with m entries, and we are again interested in AΛ = 0. As we saw previously, this is equivalent to a list of n equations. Consider the first m rows of A, the first m equations; any solution of the full list of equations must also be true of the reduced list. In fact, if 〈i1,...,im〉 is any list of m rows, then the equation must be true for those rows.
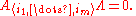
Furthermore, the reverse is true. That is, we can test whether the m vectors are linearly dependent by testing whether
for all possible lists of m rows. (In case m = n, this requires only one determinant, as above. If m > n, then it is a theorem that the vectors must be linearly dependent.) This fact is valuable for theory; in practical calculations more efficient methods are available.
Example II
Let V = Rn and consider the following elements in V: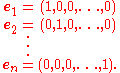Then e1, e2, ..., en are linearly independent.
Proof
Suppose that a1, a2, ..., an are elements of R such thatSince
then ai = 0 for all i in {1, ..., n}.
Example III
Let V be the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of all function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s of a real variable t. Then the functions et and e2t in V are linearly independent.
Proof
Suppose a and b are two real numbers such that- aet + be2t = 0
for all values of t. We need to show that a = 0 and b = 0. In order to do this, we divide through by et (which is never zero) and subtract to obtain
- bet = −a.
In other words, the function bet must be independent of t, which only occurs when b = 0. It follows that a is also zero.
Example IV
The following vectors in R4 are linearly dependent.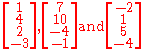Proof
We need to find scalars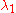, 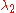and 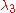such that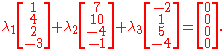Forming the simultaneous equations:
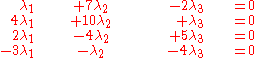
we can solve (using, for example, Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
) to obtain:
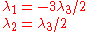
where
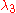can be chosen arbitrarily.Since these are nontrivial results, the vectors are linearly dependent.
Projective space of linear dependences
A linear dependence among vectors v1, ..., vn is a tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
(a1, ..., an) with n scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
components, not all zero, such that
If such a linear dependence exists, then the n vectors are linearly dependent. It makes sense to identify two linear dependences if one arises as a non-zero multiple of the other, because in this case the two describe the same linear relationship among the vectors. Under this identification, the set of all linear dependences among v1, ...., vn is a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
.
Linear dependence between random variables
The covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
is sometimes called a measure of "linear dependence" between two random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. That does not mean the same thing as in the context of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. When the covariance is normalized, one obtains the correlation matrix. From it, one can obtain the Pearson coefficient, which gives us the goodness of the fit for the best possible linear function
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
describing the relation between the variables. In this sense covariance is a linear gauge of dependence.
See also
- OrthogonalityOrthogonalityOrthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
- MatroidMatroidIn combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
– a generalization of the concept - Linear independence of functions
- Gram determinant
External links
- Online Notes on Linear Independence.
- Linearly Dependent Functions at WolframMathWorld.
- Tutorial and interactive program on Linear Independence.
- Introduction to Linear Independence at KhanAcademy.