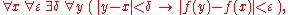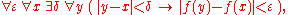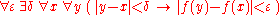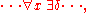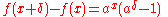Uniform continuity
Encyclopedia
In mathematics
, a function
f is uniformly continuous if, roughly speaking, it is possible to guarantee that f(x) and f(y) be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot depend on x and y themselves. For instance, any isometry
(distance-preserving map) between metric space
s is uniformly continuous.
Every uniformly continuous function between metric spaces is continuous
. Uniform continuity, unlike continuity, relies on the ability to compare the sizes of neighbourhood
s of distinct points of a given space. In an arbitrary topological space
this may not be possible. Instead, uniform continuity can be defined on a metric space where such comparisons are possible, or more generally on a uniform space
.
The equicontinuity
of a set of functions is a generalization of the concept of uniform continuity.
Every continuous function on a closed and bounded (i.e., compact) interval is uniformly continuous.
ε > 0 there exists δ > 0 such that for every x, y ∈ X with d1(x, y) < δ, we have that d2(f(x), f(y)) < ε.
If X and Y are subsets of the real number
s, d1 and d2 can be the standard Euclidean norm, || · ||, yielding the definition: for all ε > 0 there exists a δ > 0 such that for all x, y ∈ X, |x − y| < δ implies |f(x) − f(y)| < ε.
The difference between being uniformly continuous, and simply being continuous at every point, is that in uniform continuity the value of δ depends only on ε and not on the point in the domain.
itself is a local (more precisely, pointwise) property of a function—that is, a function f is continuous, or not, at a particular point. When we speak of a function being continuous on an interval
, we mean only that it is continuous at each point of the interval. In contrast, uniform continuity is a global property of f, in the sense that the standard definition refers to pairs of points rather than individual points. On the other hand, it is possible to give a local definition in terms of the natural extension f*, see below.
, but the converse does not hold. Consider for instance the function
. Given an arbitrarily small positive real number 
, uniform continuity requires the existence of a positive number 
such that for all 
with 
, we have 
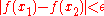. But
and for all sufficiently large x this quantity is greater than
.
The image of a totally bounded
subset under a uniformly continuous function is totally bounded. However, the image of a bounded subset of an arbitrary metric space under a uniformly continuous function need not be bounded as is shown by the counterexample of the identity function from the integers endowed with the discrete metric to the integers endowed with the usual Euclidean metric.
The Heine–Cantor theorem
asserts that every continuous function on a compact set is uniformly continuous. In particular, if a function is continuous on a closed bounded interval
of the real line, it is uniformly continuous on that interval. The Darboux integrability
of continuous functions follows almost immediately from the uniform continuity theorem.
If a real-valued function
is continuous on 
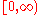and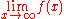 
exists (and is finite), then 
is uniformly continuous. In particular, every element of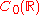 
, the space of continuous functions on 
that vanish at infinity, is uniformly continuous. This is a generalization of the Heine-Cantor theorem mentioned above, since 
.
, a real-valued function f of a real variable is microcontinuous at a point a precisely if the difference f(a + δ) − f(a) is infinitesimal whenever δ is infinitesimal. Thus f is continuous on a set A in R precisely if such f is microcontinuous at every real point a ∈ A. Uniform continuity can be expressed as the condition that (the natural extension of) f is microcontinuous not only at real points in A, but at all points in its non-standard counterpart (natural extension) *A in *R (see non-standard calculus
for more details and examples).
we have
Continuity of a function for every point x of an interval can thus be expressed by a formula starting with the quantification
which is equivalent to
whereas for uniform continuity, the order of the second and third quantifiers is reversed:
(the domains of the variables have been deliberately left out so as to emphasize quantifier order). Thus for continuity at each point, one takes an arbitrary point x, and then there must exist a distance δ,
while for uniform continuity a single δ must work ("uniformly") for all points x (and y):
a
continuous function. When can f be extended to a continuous function on all of X?
If S is closed in X, the answer is given by the Tietze extension theorem: always. So it is necessary and sufficient to extend f to the closure of S in X: that is, we may assume without loss of generality that S is dense in X, and this has the further pleasant consequence that if the extension exists, it is unique.
Let us suppose moreover that X is complete, so that X is
the completion of S. Then a continuous function
extends to all of X if and only if f is Cauchy-continuous
, i. e., the image under f of a Cauchy sequence remains Cauchy. (In general, Cauchy continuity is necessary and sufficient for extension of f to the completion of X, so is a priori stronger than extendability to X.)
It is easy to see that every uniformly continuous function is Cauchy-continuous and thus extends to X. The converse does not hold, since the function
is, as seen above, not uniformly continuous, but it is continuous and thus -- since R is complete -- Cauchy continuous. In general, for functions defined on unbounded spaces like R, uniform continuity is a rather strong condition. It is desirable to have a weaker condition from which to deduce extendability.
For example, suppose a > 1 is a real number. At the precalculus level, the function
can be given a precise definition only for rational values of x (assuming the existence of qth roots of positive real numbers, an application of the Intermediate Value Theorem). One would like to extend f to a function defined on all of R. The identity
shows that f is not uniformly continuous on all of Q; however for any bounded interval I the restriction of f to
is uniformly continuous, hence Cauchy-continuous, hence f extends to a continuous function on I. But since this holds for every I, there is then a unique extension of f to a continuous function on all of R.
More generally, a continuous function
whose restriction to every bounded subset of S is uniformly continuous is extendable to X, and the converse holds if X is locally compact.
A typical application of the extendability of a uniform continuous function is the proof of the inverse Fourier transformation formula. We first prove that the formula is true for test functions, there are densely many of them. We then extend the inverse map to the whole space using the fact that linear map is continuous; thus, uniformly continuous.
and 
, the notion of uniform continuity of a map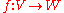 
becomes: for any neighborhood 
of zero in 
, there exists a neighborhood 
of zero in 
such that 
implies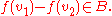 
For linear transformation
s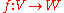
, uniform continuity is equivalent to continuity. This fact is frequently used implicitly in functional analysis
to extend a linear map off a dense subspace of a Banach space
.
s,
the most natural and general setting for the study of uniform continuity are the uniform space
s.
A function f : X → Y between uniform space is called uniformly continuous if for every entourage V in Y there exists an entourage U in X such that for every (x1, x2) in U we have (f(x1), f(x2)) in V.
In this setting, it is also true that uniformly continuous maps transform Cauchy sequences into Cauchy sequences and that continuous maps on compact uniform spaces are automatically uniformly continuous.
Each compact Hausdorff space possesses exactly one uniform structure compatible with the topology. A consequence is a generalisation of the Heine-Cantor theorem: each continuous function from a compact Hausdorff space to a uniform space is uniformly continuous.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f is uniformly continuous if, roughly speaking, it is possible to guarantee that f(x) and f(y) be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot depend on x and y themselves. For instance, any isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
(distance-preserving map) between metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s is uniformly continuous.
Every uniformly continuous function between metric spaces is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Uniform continuity, unlike continuity, relies on the ability to compare the sizes of neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
s of distinct points of a given space. In an arbitrary topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
this may not be possible. Instead, uniform continuity can be defined on a metric space where such comparisons are possible, or more generally on a uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
.
The equicontinuity
Equicontinuity
In mathematical analysis, a family of functions is equicontinuous if all the functions are continuous and they have equal variation over a given neighbourhood, in a precise sense described herein...
of a set of functions is a generalization of the concept of uniform continuity.
Every continuous function on a closed and bounded (i.e., compact) interval is uniformly continuous.
Definition for functions on metric spaces
Given metric spaces (X, d1) and (Y, d2), a function f : X → Y is called uniformly continuous if for every real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
ε > 0 there exists δ > 0 such that for every x, y ∈ X with d1(x, y) < δ, we have that d2(f(x), f(y)) < ε.
If X and Y are subsets of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, d1 and d2 can be the standard Euclidean norm, || · ||, yielding the definition: for all ε > 0 there exists a δ > 0 such that for all x, y ∈ X, |x − y| < δ implies |f(x) − f(y)| < ε.
The difference between being uniformly continuous, and simply being continuous at every point, is that in uniform continuity the value of δ depends only on ε and not on the point in the domain.
Local versus global
ContinuityContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
itself is a local (more precisely, pointwise) property of a function—that is, a function f is continuous, or not, at a particular point. When we speak of a function being continuous on an interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
, we mean only that it is continuous at each point of the interval. In contrast, uniform continuity is a global property of f, in the sense that the standard definition refers to pairs of points rather than individual points. On the other hand, it is possible to give a local definition in terms of the natural extension f*, see below.
Examples and properties
- Every Lipschitz continuous map between two metric spaces is uniformly continuous. In particular, every function which is differentiable and has bounded derivative is uniformly continuous. More generally, every Hölder continuous function is uniformly continuous.
- Every member of a uniformly equicontinuous set of functions is uniformly continuous.
- The tangent function is continuous on the interval (−π/2, π/2) but is not uniformly continuous on that interval.
- The exponential function x
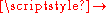ex is continuous everywhere on the real line but is not uniformly continuous on the line.
Properties
Every uniformly continuous function is continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, but the converse does not hold. Consider for instance the function
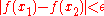. Given an arbitrarily small positive real number , uniform continuity requires the existence of a positive number such that for all with , we have . But
and for all sufficiently large x this quantity is greater than
.The image of a totally bounded
Totally bounded space
In topology and related branches of mathematics, a totally bounded space is a space that can be covered by finitely many subsets of any fixed "size" . The smaller the size fixed, the more subsets may be needed, but any specific size should require only finitely many subsets...
subset under a uniformly continuous function is totally bounded. However, the image of a bounded subset of an arbitrary metric space under a uniformly continuous function need not be bounded as is shown by the counterexample of the identity function from the integers endowed with the discrete metric to the integers endowed with the usual Euclidean metric.
The Heine–Cantor theorem
Heine–Cantor theorem
In mathematics, the Heine–Cantor theorem, named after Eduard Heine and Georg Cantor, states that if M and N are metric spaces and M is compact then every continuous functionis uniformly continuous....
asserts that every continuous function on a compact set is uniformly continuous. In particular, if a function is continuous on a closed bounded interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of the real line, it is uniformly continuous on that interval. The Darboux integrability
Darboux integral
In real analysis, a branch of mathematics, the Darboux integral or Darboux sum is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of...
of continuous functions follows almost immediately from the uniform continuity theorem.
If a real-valued function
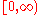is continuous on and 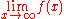exists (and is finite), then is uniformly continuous. In particular, every element of 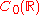, the space of continuous functions on that vanish at infinity, is uniformly continuous. This is a generalization of the Heine-Cantor theorem mentioned above, since .Non-standard analysis
In non-standard analysisNon-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
, a real-valued function f of a real variable is microcontinuous at a point a precisely if the difference f(a + δ) − f(a) is infinitesimal whenever δ is infinitesimal. Thus f is continuous on a set A in R precisely if such f is microcontinuous at every real point a ∈ A. Uniform continuity can be expressed as the condition that (the natural extension of) f is microcontinuous not only at real points in A, but at all points in its non-standard counterpart (natural extension) *A in *R (see non-standard calculus
Non-standard calculus
In mathematics, non-standard calculus is the modern application of infinitesimals, in the sense of non-standard analysis, to differential and integral calculus...
for more details and examples).
Characterization via sequences
For a function between Euclidean spaces, uniform continuity can be defined in terms of how the function behaves on sequences . More specifically, let A be a subset of Rn. A function f : A → Rm is uniformly continuous if and only if for every pair of sequences xn and yn such thatwe have
Relationship with Continuity
The mathematical statements that a function is continuous on an interval I and the definition that a function is uniformly continuous on the same interval are structurally very similar.Continuity of a function for every point x of an interval can thus be expressed by a formula starting with the quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
which is equivalent to
whereas for uniform continuity, the order of the second and third quantifiers is reversed:
(the domains of the variables have been deliberately left out so as to emphasize quantifier order). Thus for continuity at each point, one takes an arbitrary point x, and then there must exist a distance δ,
while for uniform continuity a single δ must work ("uniformly") for all points x (and y):
Relations with the extension problem
Let X be a metric space, S a subset of X, and acontinuous function. When can f be extended to a continuous function on all of X?
If S is closed in X, the answer is given by the Tietze extension theorem: always. So it is necessary and sufficient to extend f to the closure of S in X: that is, we may assume without loss of generality that S is dense in X, and this has the further pleasant consequence that if the extension exists, it is unique.
Let us suppose moreover that X is complete, so that X is
the completion of S. Then a continuous function
extends to all of X if and only if f is Cauchy-continuousCauchy-continuous function
In mathematics, a Cauchy-continuous, or Cauchy-regular, function is a special kind of continuous function between metric spaces...
, i. e., the image under f of a Cauchy sequence remains Cauchy. (In general, Cauchy continuity is necessary and sufficient for extension of f to the completion of X, so is a priori stronger than extendability to X.)
It is easy to see that every uniformly continuous function is Cauchy-continuous and thus extends to X. The converse does not hold, since the function
is, as seen above, not uniformly continuous, but it is continuous and thus -- since R is complete -- Cauchy continuous. In general, for functions defined on unbounded spaces like R, uniform continuity is a rather strong condition. It is desirable to have a weaker condition from which to deduce extendability.For example, suppose a > 1 is a real number. At the precalculus level, the function
can be given a precise definition only for rational values of x (assuming the existence of qth roots of positive real numbers, an application of the Intermediate Value Theorem). One would like to extend f to a function defined on all of R. The identity
shows that f is not uniformly continuous on all of Q; however for any bounded interval I the restriction of f to
is uniformly continuous, hence Cauchy-continuous, hence f extends to a continuous function on I. But since this holds for every I, there is then a unique extension of f to a continuous function on all of R.More generally, a continuous function
whose restriction to every bounded subset of S is uniformly continuous is extendable to X, and the converse holds if X is locally compact.A typical application of the extendability of a uniform continuous function is the proof of the inverse Fourier transformation formula. We first prove that the formula is true for test functions, there are densely many of them. We then extend the inverse map to the whole space using the fact that linear map is continuous; thus, uniformly continuous.
Generalization to topological vector spaces
In the special case of two topological vector spaces and , the notion of uniform continuity of a map 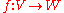becomes: for any neighborhood of zero in , there exists a neighborhood of zero in such that implies 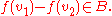For linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s
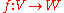, uniform continuity is equivalent to continuity. This fact is frequently used implicitly in functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
to extend a linear map off a dense subspace of a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
Generalization to uniform spaces
Just as the most natural and general setting for continuity is topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s,
the most natural and general setting for the study of uniform continuity are the uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s.
A function f : X → Y between uniform space is called uniformly continuous if for every entourage V in Y there exists an entourage U in X such that for every (x1, x2) in U we have (f(x1), f(x2)) in V.
In this setting, it is also true that uniformly continuous maps transform Cauchy sequences into Cauchy sequences and that continuous maps on compact uniform spaces are automatically uniformly continuous.
Each compact Hausdorff space possesses exactly one uniform structure compatible with the topology. A consequence is a generalisation of the Heine-Cantor theorem: each continuous function from a compact Hausdorff space to a uniform space is uniformly continuous.