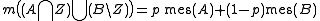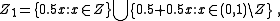Standard probability space
Encyclopedia
In probability theory
, a standard probability space (called also Lebesgue–Rokhlin probability space or just Lebesgue space; the latter term is ambiguous) is a probability space
satisfying certain assumptions introduced by Vladimir Rokhlin in 1940. He showed that the unit interval
endowed with the Lebesgue measure
has important advantages over general probability spaces, and can be used as a probability space for all practical purposes in probability theory. The theory of standard probability spaces was started by von Neumann
in 1932 and shaped by Vladimir Rokhlin in 1940. The dimension of the unit interval is not a concern, which was clear already to Norbert Wiener
. He constructed the Wiener process
(also called Brownian motion
) in the form of a measurable map
from the unit interval to the space of continuous functions
.
in 1932 and shaped by Vladimir Rokhlin in 1940. For modernized presentations see , , and .
Nowadays standard probability spaces may be (and often are) treated in the framework of descriptive set theory
, via standard Borel spaces
, see for example . This approach, natural for experts in descriptive set theory, is based on the isomorphism theorem for standard Borel spaces whose proof is very difficult for non-experts in descriptive set theory. The original approach of Rokhlin, based on measure theory, leads to much simpler proofs (since measure theory may neglect null set
s, in contrast to descriptive set theory).
Standard probability spaces are used routinely in ergodic theory
, which cannot be said on probability theory. Some probabilists hold the following opinion: only standard probability spaces are pertinent to probability theory, thus, it is a pity that the standardness is not included into the definition of probability space. Others disagree, however.
Arguments against standardness:
Arguments in favour of standardness:
s are assumed to be complete
.
between two probability spaces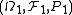 ,
, 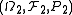 is an invertible
is an invertible
map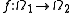 such that
such that 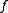 and
and 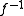 both are (measurable and) measure preserving maps.
both are (measurable and) measure preserving maps.
Two probability spaces are isomorphic, if there exists an isomorphism between them.
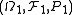 ,
,  are isomorphic
are isomorphic 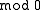 , if there exist null set
, if there exist null set
s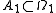 ,
,  such that the probability spaces
such that the probability spaces 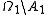 ,
, 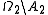 are isomorphic (being endowed naturally with sigma-fields and probability measures).
are isomorphic (being endowed naturally with sigma-fields and probability measures).
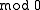 to an interval with Lebesgue measure, a finite or countable set of atoms, or a combination (disjoint union) of both.
to an interval with Lebesgue measure, a finite or countable set of atoms, or a combination (disjoint union) of both.
See , , and . See also , and . In the measure is assumed finite, not necessarily probabilistic. In atoms are not allowed.
 may be thought of as the product
may be thought of as the product  of a continuum of copies of the real line
of a continuum of copies of the real line  . One may endow
. One may endow 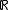 with a probability measure, say, the standard normal distribution
with a probability measure, say, the standard normal distribution  , and treat the space of functions as the product
, and treat the space of functions as the product 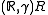 of a continuum of identical probability spaces
of a continuum of identical probability spaces 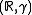 . The product measure
. The product measure
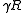 is a probability measure on
is a probability measure on 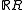 . Many non-experts are inclined to believe that
. Many non-experts are inclined to believe that 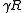 describes the so-called white noise
describes the so-called white noise
.
However, it does not. For the white noise, its integral from 0 to 1 should be a random variable distributed N(0, 1). In contrast, the integral (from 0 to 1) of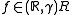 is undefined. Even worse, ƒ fails to be almost surely
is undefined. Even worse, ƒ fails to be almost surely
measurable. Still worse, the probability of ƒ being measurable is undefined. And the worst thing: if X is a random variable distributed (say) uniformly on (0, 1) and independent of ƒ, then ƒ(X) is not a random variable at all! (It lacks measurability.)
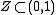 be a set whose inner
be a set whose inner
Lebesgue measure is equal to 0, but outer
Lebesgue measure – to 1 (thus,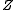 is nonmeasurable to extreme). There exists a probability measure
is nonmeasurable to extreme). There exists a probability measure 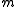 on
on 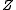 such that
such that  for every Lebesgue measurable
for every Lebesgue measurable  . (Here
. (Here 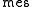 is the Lebesgue measure.) Events and random variables on the probability space
is the Lebesgue measure.) Events and random variables on the probability space 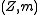 (treated
(treated 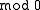 ) are in a natural one-to-one correspondence with events and random variables on the probability space
) are in a natural one-to-one correspondence with events and random variables on the probability space 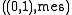 . Many non-experts are inclined to conclude that the probability space
. Many non-experts are inclined to conclude that the probability space  is as good as
is as good as  .
.
However, it is not. A random variable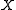 defined by
defined by 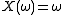 is distributed uniformly on
is distributed uniformly on  . The conditional measure, given
. The conditional measure, given 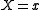 , is just a single atom (at
, is just a single atom (at  ), provided that
), provided that 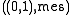 is the underlying probability space. However, if
is the underlying probability space. However, if 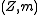 is used instead, then the conditional measure does not exist when
is used instead, then the conditional measure does not exist when 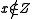 .
.
A perforated circle is constructed similarly. Its events and random variables are the same as on the usual circle. The group of rotations acts on them naturally. However, it fails to act on the perforated circle.
See also .
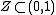 be as in the previous example. Sets of the form
be as in the previous example. Sets of the form 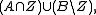 where
where 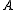 and
and 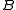 are arbitrary Lebesgue measurable sets, are a σ-algebra
are arbitrary Lebesgue measurable sets, are a σ-algebra 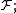 it contains the Lebesgue σ-algebra and
it contains the Lebesgue σ-algebra and  The formula
The formula
gives the general form of a probability measure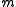 on
on 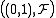 that extends the Lebesgue measure; here
that extends the Lebesgue measure; here 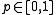 is a parameter. To be specific, we choose
is a parameter. To be specific, we choose 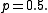 Many non-experts are inclined to believe that such an extension of the Lebesgue measure is at least harmless.
Many non-experts are inclined to believe that such an extension of the Lebesgue measure is at least harmless.
However, it is the perforated interval in disguise. The map
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a standard probability space (called also Lebesgue–Rokhlin probability space or just Lebesgue space; the latter term is ambiguous) is a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
satisfying certain assumptions introduced by Vladimir Rokhlin in 1940. He showed that the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
endowed with the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
has important advantages over general probability spaces, and can be used as a probability space for all practical purposes in probability theory. The theory of standard probability spaces was started by von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
in 1932 and shaped by Vladimir Rokhlin in 1940. The dimension of the unit interval is not a concern, which was clear already to Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
. He constructed the Wiener process
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
(also called Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
) in the form of a measurable map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
from the unit interval to the space of continuous functions
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
.
Short history
The theory of standard probability spaces was started by von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
in 1932 and shaped by Vladimir Rokhlin in 1940. For modernized presentations see , , and .
Nowadays standard probability spaces may be (and often are) treated in the framework of descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, via standard Borel spaces
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
, see for example . This approach, natural for experts in descriptive set theory, is based on the isomorphism theorem for standard Borel spaces whose proof is very difficult for non-experts in descriptive set theory. The original approach of Rokhlin, based on measure theory, leads to much simpler proofs (since measure theory may neglect null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
s, in contrast to descriptive set theory).
Standard probability spaces are used routinely in ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, which cannot be said on probability theory. Some probabilists hold the following opinion: only standard probability spaces are pertinent to probability theory, thus, it is a pity that the standardness is not included into the definition of probability space. Others disagree, however.
Arguments against standardness:
- the definition of standardness is technically demanding;
- the same about the theorems based on that definition;
- it is possible (and natural) to build all the probability theory without the standardness;
- eventsEvent (probability theory)In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
and random variables are essential, while probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
s are auxiliary and should not be taken too seriously.
Arguments in favour of standardness:
- conditioningConditioning (probability)Beliefs depend on the available information. This idea is formalized in probability theory by conditioning. Conditional probabilities, conditional expectations and conditional distributions are treated on three levels: discrete probabilities, probability density functions, and measure theory...
is easy and natural on standard probability spaces, otherwise it becomes obscure; - the same for measure-preserving transformations between probability spaces, group actions on a probability space, etc.;
- ergodic theoryErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
uses standard probability spaces routinely and successfully; - being unable to eliminate these (auxiliary) probability spaces, we should make them as useful as possible.
Definition
One of several well-known equivalent definitions of the standardness is given below, after some preparations. All probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
s are assumed to be complete
Complete measure
In mathematics, a complete measure is a measure space in which every subset of every null set is measurable...
.
Isomorphism
An isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between two probability spaces
 ,
,  is an invertible
is an invertibleInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
map
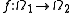 such that
such that 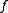 and
and 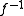 both are (measurable and) measure preserving maps.
both are (measurable and) measure preserving maps.Two probability spaces are isomorphic, if there exists an isomorphism between them.
Isomorphism modulo zero
Two probability spaces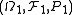 ,
,  are isomorphic
are isomorphic 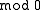 , if there exist null set
, if there exist null setNull set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
s
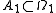 ,
,  such that the probability spaces
such that the probability spaces 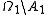 ,
, 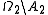 are isomorphic (being endowed naturally with sigma-fields and probability measures).
are isomorphic (being endowed naturally with sigma-fields and probability measures).Standard probability space
A probability space is standard, if it is isomorphic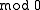 to an interval with Lebesgue measure, a finite or countable set of atoms, or a combination (disjoint union) of both.
to an interval with Lebesgue measure, a finite or countable set of atoms, or a combination (disjoint union) of both.See , , and . See also , and . In the measure is assumed finite, not necessarily probabilistic. In atoms are not allowed.
A naive white noise
The space of all functions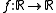 may be thought of as the product
may be thought of as the product 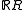 of a continuum of copies of the real line
of a continuum of copies of the real line 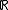 . One may endow
. One may endow 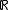 with a probability measure, say, the standard normal distribution
with a probability measure, say, the standard normal distribution  , and treat the space of functions as the product
, and treat the space of functions as the product 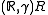 of a continuum of identical probability spaces
of a continuum of identical probability spaces 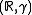 . The product measure
. The product measureProduct measure
In mathematics, given two measurable spaces and measures on them, one can obtain the product measurable space and the product measure on that space...
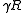 is a probability measure on
is a probability measure on 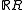 . Many non-experts are inclined to believe that
. Many non-experts are inclined to believe that 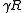 describes the so-called white noise
describes the so-called white noiseWhite noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
.
However, it does not. For the white noise, its integral from 0 to 1 should be a random variable distributed N(0, 1). In contrast, the integral (from 0 to 1) of
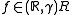 is undefined. Even worse, ƒ fails to be almost surely
is undefined. Even worse, ƒ fails to be almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
measurable. Still worse, the probability of ƒ being measurable is undefined. And the worst thing: if X is a random variable distributed (say) uniformly on (0, 1) and independent of ƒ, then ƒ(X) is not a random variable at all! (It lacks measurability.)
A perforated interval
Let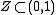 be a set whose inner
be a set whose innerInner measure
In mathematics, in particular in measure theory, an inner measure is a function on the set of all subsets of members of a given σ-algebra with values in the extended real numbers satisfying some technical conditions...
Lebesgue measure is equal to 0, but outer
Outer measure
In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
Lebesgue measure – to 1 (thus,
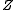 is nonmeasurable to extreme). There exists a probability measure
is nonmeasurable to extreme). There exists a probability measure 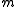 on
on 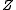 such that
such that  for every Lebesgue measurable
for every Lebesgue measurable  . (Here
. (Here 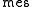 is the Lebesgue measure.) Events and random variables on the probability space
is the Lebesgue measure.) Events and random variables on the probability space 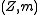 (treated
(treated 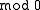 ) are in a natural one-to-one correspondence with events and random variables on the probability space
) are in a natural one-to-one correspondence with events and random variables on the probability space 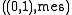 . Many non-experts are inclined to conclude that the probability space
. Many non-experts are inclined to conclude that the probability space  is as good as
is as good as  .
.However, it is not. A random variable
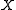 defined by
defined by 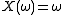 is distributed uniformly on
is distributed uniformly on  . The conditional measure, given
. The conditional measure, given 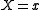 , is just a single atom (at
, is just a single atom (at  ), provided that
), provided that 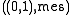 is the underlying probability space. However, if
is the underlying probability space. However, if 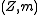 is used instead, then the conditional measure does not exist when
is used instead, then the conditional measure does not exist when 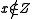 .
.A perforated circle is constructed similarly. Its events and random variables are the same as on the usual circle. The group of rotations acts on them naturally. However, it fails to act on the perforated circle.
See also .
A superfluous measurable set
Let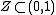 be as in the previous example. Sets of the form
be as in the previous example. Sets of the form 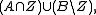 where
where 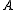 and
and 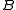 are arbitrary Lebesgue measurable sets, are a σ-algebra
are arbitrary Lebesgue measurable sets, are a σ-algebra 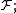 it contains the Lebesgue σ-algebra and
it contains the Lebesgue σ-algebra and  The formula
The formula
gives the general form of a probability measure
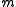 on
on 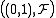 that extends the Lebesgue measure; here
that extends the Lebesgue measure; here 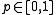 is a parameter. To be specific, we choose
is a parameter. To be specific, we choose 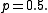 Many non-experts are inclined to believe that such an extension of the Lebesgue measure is at least harmless.
Many non-experts are inclined to believe that such an extension of the Lebesgue measure is at least harmless.However, it is the perforated interval in disguise. The map
-
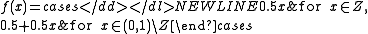
is an isomorphism between and the perforated interval corresponding to the set
and the perforated interval corresponding to the set
another set of inner Lebesgue measure 0 but outer Lebesgue measure 1.
See also .
A criterion of standardness
Standardness of a given probability space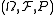 is equivalent to a certain property of a measurable map
is equivalent to a certain property of a measurable map  from
from 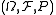 to a measurable space
to a measurable space 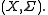 Interestingly, the answer (standard, or not) does not depend on the choice of
Interestingly, the answer (standard, or not) does not depend on the choice of 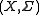 and
and 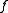 . This fact is quite useful; one may adapt the choice of
. This fact is quite useful; one may adapt the choice of  and
and 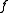 to the given
to the given 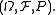 No need to examine all cases. It may be convenient to examine a random variable
No need to examine all cases. It may be convenient to examine a random variable 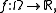 a random vector
a random vector 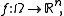 a random sequence
a random sequence 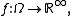 or a sequence of events
or a sequence of events  treates as a sequence of two-valued random variables,
treates as a sequence of two-valued random variables, 
Two conditions will be imposed on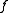 (to be injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
(to be injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
, and generating). Below it is assumed that such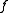 is given. The question of its existence will be addressed afterwards.
is given. The question of its existence will be addressed afterwards.
The probability space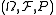 is assumed to be completeComplete measureIn mathematics, a complete measure is a measure space in which every subset of every null set is measurable...
is assumed to be completeComplete measureIn mathematics, a complete measure is a measure space in which every subset of every null set is measurable...
(otherwise it cannot be standard).
A single random variable
A measurable function induces a pushforward measurePushforward measureIn measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
induces a pushforward measurePushforward measureIn measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
, --- the probability measure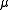 on
on 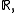 defined by
defined by
-
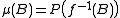 for Borel sets
for Borel sets 
(It is nothing but the distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the random variable.) The image is always a set of full outer measure,
is always a set of full outer measure,
but its inner measureInner measureIn mathematics, in particular in measure theory, an inner measure is a function on the set of all subsets of members of a given σ-algebra with values in the extended real numbers satisfying some technical conditions...
can differ (see a perforated interval). In other words, need not be a set of full measure
need not be a set of full measure 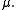
A measurable function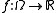 is called generating if
is called generating if 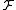 is the completion of the σ-algebra of inverse images
is the completion of the σ-algebra of inverse images  where
where 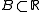 runs over all Borel sets.
runs over all Borel sets.
Caution. The following condition is not sufficient for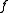 to be generating: for every
to be generating: for every 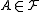 there exists a Borel set
there exists a Borel set  such that
such that  (
( means symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
means symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
).
Theorem. Let a measurable function be injective and generating, then the following two conditions are equivalent:
be injective and generating, then the following two conditions are equivalent:
-
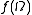 is of full measure
is of full measure 
-
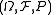 is a standard probability space.
is a standard probability space.
See also .
A random vector
The same theorem holds for any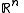 (in place of
(in place of 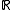 ). A measurable function
). A measurable function  may be thought of as a finite sequence of random variables
may be thought of as a finite sequence of random variables 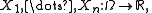 and
and  is generating if and only if
is generating if and only if  is the completion of the σ-algebra generated by
is the completion of the σ-algebra generated by 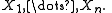
A random sequence
The theorem still holds for the space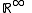 of infinite sequences. A measurable function
of infinite sequences. A measurable function 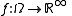 may be thought of as an infinite sequence of random variables
may be thought of as an infinite sequence of random variables 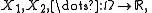 and
and 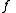 is generating if and only if
is generating if and only if  is the completion of the σ-algebra generated by
is the completion of the σ-algebra generated by 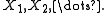
A sequence of events
In particular, if the random variables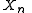 take on only two values 0 and 1, we deal with a measurable function
take on only two values 0 and 1, we deal with a measurable function 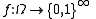 and a sequence of sets
and a sequence of sets  The function
The function  is generating if and only if
is generating if and only if 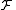 is the completion of the σ-algebra generated by
is the completion of the σ-algebra generated by 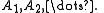
In the pioneering work sequences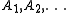 that correspond to injective, generating
that correspond to injective, generating 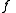 are called bases of the probability space
are called bases of the probability space 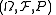 (see ). A basis is called complete mod 0, if
(see ). A basis is called complete mod 0, if 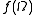 is of full measure
is of full measure 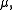 see . In the same section Rokhlin proved that if a probability space is complete mod 0 with respect to some basis, then it is complete mod 0 with respect to every other basis, and defines Lebesgue spaces by this completeness property. See also and .
see . In the same section Rokhlin proved that if a probability space is complete mod 0 with respect to some basis, then it is complete mod 0 with respect to every other basis, and defines Lebesgue spaces by this completeness property. See also and .
Additional remarks
The four cases treated above are mutually equivalent, and can be united, since the measurable spaces
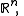
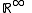 and
and 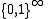 are mutually isomorphic; they all are standard measurable spaces (in other words, standard Borel spaces).
are mutually isomorphic; they all are standard measurable spaces (in other words, standard Borel spaces).
Existence of an injective measurable function from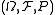 to a standard measurable space
to a standard measurable space  does not depend on the choice of
does not depend on the choice of 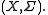 Taking
Taking 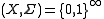 we get the property well-known as being countably separated (but called separable in ).
we get the property well-known as being countably separated (but called separable in ).
Existence of a generating measurable function from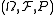 to a standard measurable space
to a standard measurable space 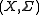 also does not depend on the choice of
also does not depend on the choice of  Taking
Taking 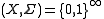 we get the property well-known as being countably generated (mod 0), see .
we get the property well-known as being countably generated (mod 0), see .
Probability space Countably separated Countably generated Standard Interval with Lebesgue measure Naive white noise Perforated interval
Every injective measurable function from a standard probability space to a standard measurable space is generating. See , , . This property does not hold for the non-standard probability space dealt with in the subsection "A superfluous measurable set" above.
Caution. The property of being countably generated is invariant under mod 0 isomorphisms, but the property of being countably separated is not. In fact, a standard probability space is countably separated if and only if the cardinality of
is countably separated if and only if the cardinality of  does not exceed continuumCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
does not exceed continuumCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
(see ). A standard probability space may contain a null set of any cardinality, thus, it need not be countably separated. However, it always contains a countably separated subset of full measure.
Equivalent definitions
Let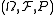 be a complete probability space such that the cardinality of
be a complete probability space such that the cardinality of 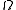 does not exceed continuum (the general case is reduced to this special case, see the caution above).
does not exceed continuum (the general case is reduced to this special case, see the caution above).
Via absolute measurability
Definition.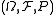 is standard if it is countably separated, countably generated, and absolutely measurable.
is standard if it is countably separated, countably generated, and absolutely measurable.
See and . "Absolutely measurable" means: measurable in every countably separated, countably generated probability space containing it.
Via perfectness
Definition.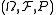 is standard if it is countably separated and perfect.
is standard if it is countably separated and perfect.
See . "Perfect" means that for every measurable function from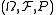 to
to  the image measure is regularRegular measureIn mathematics, a regular measure on a topological space is a measure for which every measurable set is "approximately open" and "approximately closed".-Definition:...
the image measure is regularRegular measureIn mathematics, a regular measure on a topological space is a measure for which every measurable set is "approximately open" and "approximately closed".-Definition:...
. (Here the image measure is defined on all sets whose inverse images belong to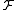 , irrespective of the Borel structure of
, irrespective of the Borel structure of  ).
).
Via topology
Definition.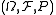 is standard if there exists a topologyTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is standard if there exists a topologyTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
 on
on 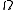 such that
such that
- the topological space
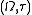 is metrizable;
is metrizable; -
 is the completion of the σ-algebra generated by
is the completion of the σ-algebra generated by  (that is, by all open sets);
(that is, by all open sets); - for every
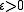 there exists a compact set
there exists a compact set 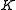 in
in  such that
such that 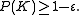
See .
Verifying the standardness
Every probability distribution on the space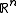 turns it into a standard probability space. (Here, a probability distribution means a probability measure defined initially on the Borel sigma-algebra and completed.)
turns it into a standard probability space. (Here, a probability distribution means a probability measure defined initially on the Borel sigma-algebra and completed.)
The same holds on every Polish spacePolish spaceIn the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
, see , , , and .
For example, the Wiener measure turns the Polish space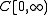 (of all continuous functions
(of all continuous functions 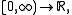 endowed with the topologyTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
endowed with the topologyTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
of local uniform convergence) into a standard probability space.
Another example: for every sequence of random variables, their joint distribution turns the Polish space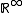 (of sequences; endowed with the product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
(of sequences; endowed with the product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
) into a standard probability space.
(Thus, the idea of dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, very natural for topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, is utterly inappropriate for standard probability spaces.)
The productProduct measureIn mathematics, given two measurable spaces and measures on them, one can obtain the product measurable space and the product measure on that space...
of two standard probability spaces is a standard probability space.
The same holds for the product of countably many spaces, see , , and .
A measurable subset of a standard probability space is a standard probability space. It is assumed that the set is not a null set, and is endowed with the conditional measure. See and .
Every probability measureProbability measureIn mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on a standard Borel space turns it into a standard probability space.
Regular conditional probabilities
In the discrete setup, the conditional probability is another probability measure, and the conditional expectation may be treated as the (usual) expectation with respect to the conditional measure, see conditional expectationConditional expectationIn probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
. In the non-discrete setup, conditioning is often treated indirectly, since the condition may have probability 0, see conditional expectationConditional expectationIn probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
. As a result, a number of well-known facts have special 'conditional' counterparts. For example: linearity of the expectation; Jensen's inequality (see conditional expectationConditional expectationIn probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
); Hölder's inequalityHölder's inequalityIn mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
; the monotone convergence theorem, etc.
Given a random variable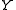 on a probability space
on a probability space  , it is natural to try constructing a conditional measure
, it is natural to try constructing a conditional measure 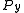 , that is, the conditional distributionConditional distributionGiven two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
, that is, the conditional distributionConditional distributionGiven two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
of given
given 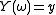 . In general this is impossible (see ). However, for a standard probability space
. In general this is impossible (see ). However, for a standard probability space  this is possible, and well-known as canonical system of measures (see ), which is basically the same as conditional probability measures (see ), disintegration of measureDisintegration theoremIn mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures...
this is possible, and well-known as canonical system of measures (see ), which is basically the same as conditional probability measures (see ), disintegration of measureDisintegration theoremIn mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures...
(see ), and regular conditional probabilitiesRegular conditional probabilityRegular conditional probability is a concept that has developed to overcome certain difficulties in formally defining conditional probabilities for continuous probability distributions...
(see ).
The conditional Jensen's inequality is just the (usual) Jensen's inequality applied to the conditional measure. The same holds for many other facts.
Measure preserving transformations
Given two probability spaces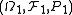 ,
,  and a measure preserving map
and a measure preserving map  , the image
, the image 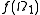 need not cover the whole
need not cover the whole 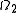 , it may miss a null set. It may seem that
, it may miss a null set. It may seem that 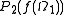 has to be equal to 1, but it is not so. The outer measure of
has to be equal to 1, but it is not so. The outer measure of  is equal to 1, but the inner measure may differ. However, if the probability spaces
is equal to 1, but the inner measure may differ. However, if the probability spaces  ,
, 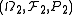 are standard then
are standard then 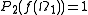 , see . If
, see . If 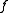 is also one-to-one then every
is also one-to-one then every 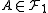 satisfies
satisfies 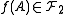 ,
, 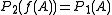 . Therefore
. Therefore 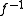 is measurable (and measure preserving). See and . See also .
is measurable (and measure preserving). See and . See also .
"There is a coherent way to ignore the sets of measure 0 in a measure space" . Striving to get rid of null sets, mathematicians often use equivalence classes of measurable sets or functions. Equivalence classes of measurable subsets of a probability space form a normed complete Boolean algebraComplete Boolean algebraIn mathematics, a complete Boolean algebra is a Boolean algebra in which every subset has a supremum . Complete Boolean algebras are used to construct Boolean-valued models of set theory in the theory of forcing...
called the measure algebra (or metric structure). Every measure preserving map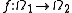 leads to a homomorphism
leads to a homomorphism  of measure algebras; basically,
of measure algebras; basically,  for
for 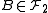 .
.
It may seem that every homomorphism of measure algebras has to correspond to some measure preserving map, but it is not so. However, for standard probability spaces each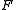 corresponds to some
corresponds to some 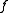 . See , , .
. See , , .
-