
Contributions of Leonhard Euler to mathematics
Encyclopedia
The 18th-century Swiss mathematician Leonhard Euler
(1707–1783) is among the most prolific and successful mathematicians in the history of the field
. His seminal work had a profound impact in numerous areas of mathematics and he is widely credited for introducing and popularizing modern notation and terminology, particularly in analysis.
, now also known as Euler's number. The use of the Greek letter
to denote the ratio of a circle's circumference to its diameter
was also popularized by Euler (although it did not originate with him). He is also credited for inventing the notation i
to denote .
.
 Euler made important contributions to complex analysis
Euler made important contributions to complex analysis
. He discovered the scientific notation. He discovered what is now known as Euler's formula
, that for any real number
 , the complex exponential function
, the complex exponential function
satisfies

This has been called "the most remarkable formula in mathematics " by Richard Feynman
.
Euler's identity is a special case of this:
This identity is particularly remarkable as it involves e, , i, 1, and 0, arguably the five most important constants in mathematics.
, i, 1, and 0, arguably the five most important constants in mathematics.
was at the forefront of 18th century mathematical research, and the Bernoullis—family friends of Euler—were responsible for much of the early progress in the field. Understanding the infinite was naturally the major focus of Euler's research. While some of Euler's proofs may not have been acceptable under modern standards of rigor, his ideas were responsible for many great advances. First of all, Euler introduced the concept of a function
, and introduced the use of the exponential function
and logarithms in analytic proofs.
Euler frequently used the logarithm function as a tool in analysis problems, and discovered new ways by which they could be used. He discovered ways to express various logarithmic functions in terms of power series, and successfully defined logarithms for complex and negative numbers, thus greatly expanding the scope where logarithms could be applied in mathematics. Most researchers in the field long held the view that for any positive real
for any positive real  since by using the additivity property of logarithms
since by using the additivity property of logarithms  . In a 1747 letter to Jean Le Rond d'Alembert
. In a 1747 letter to Jean Le Rond d'Alembert
, Euler defined the natural logarithm of -1 as a pure imaginary
a pure imaginary
.
Euler is well known in analysis for his frequent use and development of power series: that is, the expression of functions as sums of infinitely many terms, such as

Notably, Euler discovered the power series expansions for e and the inverse tangent function
 .
.
His daring (and, by modern standards, technically incorrect) use of power series enabled him to solve the famous Basel problem
in 1735:

In addition, Euler elaborated the theory of higher transcendental functions by introducing the gamma function
and introduced a new method for solving quartic equations. He also found a way to calculate integrals with complex limits, foreshadowing the development of complex analysis
. Euler invented the calculus of variations
including its most well-known result, the Euler-Lagrange equation
.
Euler also pioneered the use of analytic methods to solve number theory problems. In doing so, he united two disparate branches of mathematics and introduced a new field of study, analytic number theory
. In breaking ground for this new field, Euler created the theory of hypergeometric series
, q-series, hyperbolic trigonometric functions and the analytic theory of continued fractions. For example, he proved the infinitude of primes using the divergence of the harmonic series, and used analytic methods to gain some understanding of the way prime numbers are distributed. Euler's work in this area led to the development of the prime number theorem
.
. A lot of his early work on number theory was based on the works of Pierre de Fermat
, and developed some of Fermat's ideas.
One focus of Euler's work was to link the nature of prime distribution with ideas in analysis. He proved that the sum of the reciprocals of the primes diverges. In doing so, he discovered the connection between Riemann zeta function and prime numbers, known as the Euler product formula for the Riemann zeta function
.
Euler proved Newton's identities
, Fermat's little theorem
, Fermat's theorem on sums of two squares, and made distinct contributions to the Lagrange's four-square theorem
. He also invented the totient function φ(n) which assigns to a positive integer n the number of positive integers less than n and coprime to n. Using properties of this function he was able to generalize Fermat's little theorem to what would become known as Euler's theorem. He further contributed significantly to the understanding of perfect numbers, which had fascinated mathematicians since Euclid
. Euler made progress toward the prime number theorem and conjectured the law of quadratic reciprocity
. The two concepts are regarded as the fundamental theorems of number theory, and his ideas paved the way for Carl Friedrich Gauss
.
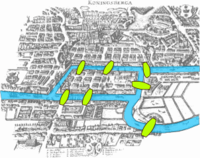 In 1736 Euler solved, or rather proved unsolvable, a problem known as the seven bridges of Königsberg. The city of Königsberg
In 1736 Euler solved, or rather proved unsolvable, a problem known as the seven bridges of Königsberg. The city of Königsberg
, Kingdom of Prussia
(now Kaliningrad, Russia) is set on the Pregel River, and included two large islands which were connected to each other and the mainland by seven bridges. The question is whether it is possible to walk with a route that crosses each bridge exactly once, and return to the starting point.
Euler's solution of the Königsberg bridge problem is considered to be the first theorem of graph theory
. In addition, his recognition that the key information was the number of bridges and the list of their endpoints (rather than their exact positions) presaged the development of topology
.
 Euler also made contributions to the understanding of planar graphs. He introduced a formula governing the relationship between the number of edges, vertices, and faces of a convex polyhedron. Given such a polyhedron, the alternating sum of vertices, edges and faces equals a constant: V-E+F=2. This constant, χ, is the Euler characteristic
Euler also made contributions to the understanding of planar graphs. He introduced a formula governing the relationship between the number of edges, vertices, and faces of a convex polyhedron. Given such a polyhedron, the alternating sum of vertices, edges and faces equals a constant: V-E+F=2. This constant, χ, is the Euler characteristic
of the plane. The study and generalization of this equation, specially by Cauchy
and Lhuillier, is at the origin of topology
. Euler characteristic, which may be generalized to any topological space
as the alternating sum of the Betti number
s, naturally arises from homology
. In particular, it is equal to 2-2g for a closed oriented surface
with genus g and to 2-k for a non-orientable surface with k crosscaps. This property led to the definition of rotation system
s in topological graph theory
.
, Fourier series
, Venn diagram
s, Euler numbers, e
and π
constants, continued fractions and integrals. He integrated Leibniz
's differential calculus
with Newton's Method of Fluxions
, and developed tools that made it easier to apply calculus to physical problems. In particular, he made great strides in improving numerical approximation
of integrals, inventing what are now known as the Euler approximations. The most notable of these approximations are Euler method and the Euler–Maclaurin formula. He also facilitated the use of differential equation
s, in particular introducing the Euler-Mascheroni constant
:

One of Euler's more unusual interests was the application of mathematical ideas in music
. In 1739 he wrote the Tentamen novae theoriae musicae, hoping to eventually integrate music theory
as part of mathematics. This part of his work, however did not receive wide attention and was once described as too mathematical for musicians and too musical for mathematicians.
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
(1707–1783) is among the most prolific and successful mathematicians in the history of the field
History of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
. His seminal work had a profound impact in numerous areas of mathematics and he is widely credited for introducing and popularizing modern notation and terminology, particularly in analysis.
Mathematical notation
Euler introduced much of the mathematical notation in use today, such as the notation f(x) to describe a function and the modern notation for the trigonometric functions. He was the first to use the letter e for the base of the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
, now also known as Euler's number. The use of the Greek letter

Pi (letter)
Pi is the sixteenth letter of the Greek alphabet, representing . In the system of Greek numerals it has a value of 80. Letters that arose from pi include Cyrillic Pe , Coptic pi , and Gothic pairthra .The upper-case letter Π is used as a symbol for:...
to denote the ratio of a circle's circumference to its diameter
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
was also popularized by Euler (although it did not originate with him). He is also credited for inventing the notation i
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
to denote
 .
.Complex analysis

Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. He discovered the scientific notation. He discovered what is now known as Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
, that for any real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
 , the complex exponential function
, the complex exponential functionExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
satisfies

This has been called "the most remarkable formula in mathematics " by Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
.
Euler's identity is a special case of this:

This identity is particularly remarkable as it involves e,
 , i, 1, and 0, arguably the five most important constants in mathematics.
, i, 1, and 0, arguably the five most important constants in mathematics.Analysis
The development of calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
was at the forefront of 18th century mathematical research, and the Bernoullis—family friends of Euler—were responsible for much of the early progress in the field. Understanding the infinite was naturally the major focus of Euler's research. While some of Euler's proofs may not have been acceptable under modern standards of rigor, his ideas were responsible for many great advances. First of all, Euler introduced the concept of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, and introduced the use of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
and logarithms in analytic proofs.
Euler frequently used the logarithm function as a tool in analysis problems, and discovered new ways by which they could be used. He discovered ways to express various logarithmic functions in terms of power series, and successfully defined logarithms for complex and negative numbers, thus greatly expanding the scope where logarithms could be applied in mathematics. Most researchers in the field long held the view that
 for any positive real
for any positive real  since by using the additivity property of logarithms
since by using the additivity property of logarithms  . In a 1747 letter to Jean Le Rond d'Alembert
. In a 1747 letter to Jean Le Rond d'AlembertJean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
, Euler defined the natural logarithm of -1 as
 a pure imaginary
a pure imaginaryComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
.
Euler is well known in analysis for his frequent use and development of power series: that is, the expression of functions as sums of infinitely many terms, such as

Notably, Euler discovered the power series expansions for e and the inverse tangent function
 .
.His daring (and, by modern standards, technically incorrect) use of power series enabled him to solve the famous Basel problem
Basel problem
The Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate...
in 1735:

In addition, Euler elaborated the theory of higher transcendental functions by introducing the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and introduced a new method for solving quartic equations. He also found a way to calculate integrals with complex limits, foreshadowing the development of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. Euler invented the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
including its most well-known result, the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
.
Euler also pioneered the use of analytic methods to solve number theory problems. In doing so, he united two disparate branches of mathematics and introduced a new field of study, analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
. In breaking ground for this new field, Euler created the theory of hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
, q-series, hyperbolic trigonometric functions and the analytic theory of continued fractions. For example, he proved the infinitude of primes using the divergence of the harmonic series, and used analytic methods to gain some understanding of the way prime numbers are distributed. Euler's work in this area led to the development of the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
.
Number theory
Euler's great interest in number theory can be traced to the influence of his friend in the St. Peterburg Academy, Christian GoldbachChristian Goldbach
Christian Goldbach was a German mathematician who also studied law. He is remembered today for Goldbach's conjecture.-Biography:...
. A lot of his early work on number theory was based on the works of Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
, and developed some of Fermat's ideas.
One focus of Euler's work was to link the nature of prime distribution with ideas in analysis. He proved that the sum of the reciprocals of the primes diverges. In doing so, he discovered the connection between Riemann zeta function and prime numbers, known as the Euler product formula for the Riemann zeta function
Proof of the Euler product formula for the Riemann zeta function
Leonhard Euler proved the Euler product formula for the Riemann zeta function in his thesis Variae observationes circa series infinitas' ', published by St Petersburg Academy in 1737.-The Euler product formula:...
.
Euler proved Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
, Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
, Fermat's theorem on sums of two squares, and made distinct contributions to the Lagrange's four-square theorem
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
. He also invented the totient function φ(n) which assigns to a positive integer n the number of positive integers less than n and coprime to n. Using properties of this function he was able to generalize Fermat's little theorem to what would become known as Euler's theorem. He further contributed significantly to the understanding of perfect numbers, which had fascinated mathematicians since Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
. Euler made progress toward the prime number theorem and conjectured the law of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
. The two concepts are regarded as the fundamental theorems of number theory, and his ideas paved the way for Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
.
Graph theory and topology

Königsberg
Königsberg was the capital of East Prussia from the Late Middle Ages until 1945 as well as the northernmost and easternmost German city with 286,666 inhabitants . Due to the multicultural society in and around the city, there are several local names for it...
, Kingdom of Prussia
Kingdom of Prussia
The Kingdom of Prussia was a German kingdom from 1701 to 1918. Until the defeat of Germany in World War I, it comprised almost two-thirds of the area of the German Empire...
(now Kaliningrad, Russia) is set on the Pregel River, and included two large islands which were connected to each other and the mainland by seven bridges. The question is whether it is possible to walk with a route that crosses each bridge exactly once, and return to the starting point.
Euler's solution of the Königsberg bridge problem is considered to be the first theorem of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. In addition, his recognition that the key information was the number of bridges and the list of their endpoints (rather than their exact positions) presaged the development of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.

Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the plane. The study and generalization of this equation, specially by Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
and Lhuillier, is at the origin of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Euler characteristic, which may be generalized to any topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
as the alternating sum of the Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s, naturally arises from homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
. In particular, it is equal to 2-2g for a closed oriented surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
with genus g and to 2-k for a non-orientable surface with k crosscaps. This property led to the definition of rotation system
Rotation system
In combinatorial mathematics, rotation systems encode embeddings of graphs onto orientable surfaces, by describing the circular ordering of a graph's edges around each vertex....
s in topological graph theory
Topological graph theory
In mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs....
.
Applied mathematics
Some of Euler's greatest successes were in applying analytic methods to real world problems, describing numerous applications of Bernoulli's numbersBernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
, Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
s, Euler numbers, e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
and π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
constants, continued fractions and integrals. He integrated Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
's differential calculus
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
with Newton's Method of Fluxions
Method of Fluxions
Method of Fluxions is a book by Isaac Newton. The book was completed in 1671, and published in 1736. Fluxions is Newton's term for differential calculus...
, and developed tools that made it easier to apply calculus to physical problems. In particular, he made great strides in improving numerical approximation
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
of integrals, inventing what are now known as the Euler approximations. The most notable of these approximations are Euler method and the Euler–Maclaurin formula. He also facilitated the use of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, in particular introducing the Euler-Mascheroni constant
Euler-Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
:

One of Euler's more unusual interests was the application of mathematical ideas in music
Music
Music is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...
. In 1739 he wrote the Tentamen novae theoriae musicae, hoping to eventually integrate music theory
Music theory
Music theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
as part of mathematics. This part of his work, however did not receive wide attention and was once described as too mathematical for musicians and too musical for mathematicians.
Works
The works which Euler published separately are:- Dissertatio physica de sono (Dissertation on the physics of sound) (Basel, 1727, in quarto)
- Mechanica, sive motus scientia analytice; expasita (St Petersburg, 1736, in 2 vols. quarto)
- Einleitung in die Arithmetik (ibid., 1738, in 2 vols. octavo), in German and Russian
- Tentamen novae theoriae musicae (ibid. 1739, in quarto)
- Methodus inveniendi lineas curvas, maximi minimive proprietate gaudentes (Lausanne, 1744, in quarto)
- Additamentum II (English translation)
- Theoria motuum planetarum et cometarum (Berlin, 1744, in quarto)
- Beantwortung, &c. or Answers to Different Questions respecting Comets (ibid., 1744, in octavo)
- Neue Grundsatze, &c. or New Principles of Artillery, translated from the English of Benjamin Robins, with notes and illustrations (ibid., 1745, in octavo)
- Opuscula varii argumenti (ibid., 1746–1751, in 3 vols. quarto)
- Novae et carrectae tabulae ad loco lunae computanda (ibid., 1746, in quarto)
- Tabulae astronomicae solis et lunae (ibid., in quarto)
- Gedanken, &c. or Thoughts on the Elements of Bodies (ibid. in quarto)
- Rettung der gall-lichen Offenbarung, &c., Defence of Divine Revelation against Free-thinkers (ibid., 1747, in quarto)
- Introductio in analysin infinitorum (Introduction to the analysis of the infinites)(Lausanne, 1748, in 2 vols. quarto)
- Scientia navalis, seu tractatus de construendis ac dirigendis navibus (St Petersburg, 1749, in 2 vols. quarto)
- Exposé concernant l’examen de la lettre de M. de Leibnitz (1752, its English translation)
- Theoria motus lunae (Berlin, 1753, in quarto)
- Dissertatio de principio mininiae actionis, una cum examine objectionum cl. prof. Koenigii (ibid., 1753, in octavo)
- Institutiones calculi differentialis, cum ejus usu in analysi Intuitorum ac doctrina serierum (ibid., 1755, in quarto)
- Constructio lentium objectivarum, &c. (St Petersburg, 1762, in quarto)
- Theoria motus corporum solidorum seu rigidorum (Rostock, 1765, in quarto)
- Institutiones, calculi integralis (St Petersburg, 1768–1770, in 3 vols. quarto)
- Lettres a une Princesse d'Allernagne sur quelques sujets de physique et de philosophie (St Petersburg, 1768–1772, in 3 vols. octavo)
- Anleitung zur Algebra Elements of Algebra (ibid., 1770, in octavo); Dioptrica (ibid., 1767–1771, in 3 vols. quarto)
- Theoria motuum lunge nova methodo pertr. arctata' (ibid., 1772, in quarto)
- Novae tabulae lunares (ibid., in octavo); La théorie complete de la construction et de la manteuvre des vaisseaux (ibid., 1773, in octavo)
- Eclaircissements svr etablissements en favour taut des veuves que des marts, without a date
- Opuscula analytica (St Petersburg, 1783–1785, in 2 vols. quarto). See Rudio, Leonhard Euler (Basel, 1884).

