
Calculus of variations
Encyclopedia
Calculus of variations is a field of mathematics
that deals with extremizing functionals
, as opposed to ordinary calculus
which deals with functions
. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown functions and their derivatives. The interest is in extremal functions that make the functional attain a maximum or minimum value – or stationary functions – those where the rate of change of the functional is precisely zero.
Perhaps the simplest example of such a problem is to find the curve of shortest length, or geodesic
, connecting two points. If there are no constraints, the solution is obviously a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as geodesic
s. A related problem is posed by Fermat's principle
: light follows the path of shortest optical length connecting two points, where the optical length depends upon the material of the medium. One corresponding concept in mechanics
is the principle of least action
.
Many important problems involve functions of several variables. Solutions of boundary value problems for the Laplace equation satisfy the Dirichlet principle. Plateau's problem
requires finding a surface of minimal area that spans a given contour in space: the solution or solutions can often be found by dipping a wire frame in a solution of soap suds. Although such experiments are relatively easy to perform, their mathematical interpretation is far from simple: there may be more than one locally minimizing surface, and they may have non-trivial topology.
problem raised by Johann Bernoulli
(1696). It immediately occupied the attention of Jakob Bernoulli and the Marquis de l'Hôpital
, but Leonhard Euler
first elaborated the subject. His contributions began in 1733, and his Elementa Calculi Variationum gave to the science its name. Lagrange
contributed extensively to the theory, and Legendre
(1786) laid down a method, not entirely satisfactory, for the discrimination of maxima and minima. Isaac Newton
and Gottfried Leibniz
also gave some early attention to the subject. To this discrimination Vincenzo Brunacci (1810), Carl Friedrich Gauss
(1829), Siméon Poisson (1831), Mikhail Ostrogradsky (1834), and Carl Jacobi
(1837) have been among the contributors. An important general work is that of Sarrus
(1842) which was condensed and improved by Cauchy (1844). Other valuable treatises and memoirs have been written by Strauch
(1849), Jellett (1850), Otto Hesse
(1857), Alfred Clebsch
(1858), and Carll (1885), but perhaps the most important work of the century is that of Weierstrass. His celebrated course on the theory is epoch-making, and it may be asserted that he was the first to place it on a firm and unquestionable foundation. The 20th
and the 23rd
Hilbert problems published in 1900 enticed further development. In the 20th century David Hilbert
, Emmy Noether
, Leonida Tonelli
, Henri Lebesgue
and Jacques Hadamard
among others made significant contributions. Marston Morse
applied calculus of variations in what is now called Morse theory
. Lev Pontryagin, Ralph Rockafellar
and Clarke
developed new mathematical tools for optimal control theory, a generalisation of calculus of variations.
 is defined as
is defined as
A functional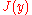 defined on some appropriate space of functions
defined on some appropriate space of functions  with norm
with norm 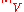 is said to have a weak minimum at the function
is said to have a weak minimum at the function 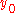 if there exists some
if there exists some  such that, for all functions y with
such that, for all functions y with 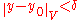 ,
,
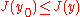 .
.
Weak maxima are defined similarly, with the inequality in the last equation reversed. In most problems, is the space of r-times continuously differentiable functions on a compact subset
is the space of r-times continuously differentiable functions on a compact subset  of the real line, with its norm given by
of the real line, with its norm given by
 .
.
This norm is just the sum of the supremum norms of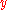 and its derivatives.
and its derivatives.
A functional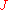 is said to have a strong minimum at
is said to have a strong minimum at  if there exists some
if there exists some  such that, for all functions
such that, for all functions 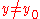 with
with 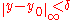 ,
,  . Strong maximum is defined similarly, but with the inequality in the last equation reversed.
. Strong maximum is defined similarly, but with the inequality in the last equation reversed.
The difference between strong and weak extrema is that, for a strong extremum,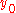 is a local extremum relative to the set of
is a local extremum relative to the set of  -close functions with respect to the supremum norm. In general this (supremum) norm is different from the norm
-close functions with respect to the supremum norm. In general this (supremum) norm is different from the norm 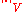 that V has been endowed with. If
that V has been endowed with. If 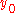 is a strong extremum for
is a strong extremum for 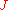 then it is also a weak extremum, but the converse may not hold. Finding strong extrema is more difficult than finding weak extrema and in what follows it will be assumed that we are looking for weak extrema.
then it is also a weak extremum, but the converse may not hold. Finding strong extrema is more difficult than finding weak extrema and in what follows it will be assumed that we are looking for weak extrema.
Consider the functional:
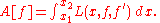
The function should have at least one derivative in order to satisfy the requirements for valid application of the function; further, if the functional
should have at least one derivative in order to satisfy the requirements for valid application of the function; further, if the functional 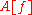 attains its local minimum at
attains its local minimum at 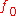 and
and 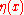 is an arbitrary function that has at least one derivative and vanishes at the endpoints
is an arbitrary function that has at least one derivative and vanishes at the endpoints 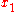 and
and  , then we must have
, then we must have
for any number ε close to 0. Therefore, the derivative of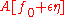 with respect to ε (the first variation
with respect to ε (the first variation
of A) must vanish at ε = 0.
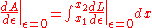
Since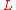 is a function of
is a function of  and
and 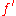 , the term
, the term

with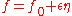 . Therefore,
. Therefore,
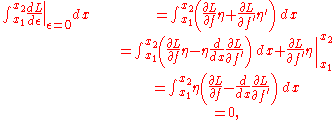
where we have used the chain rule
in the second line and integration by parts
in the third. The last term in the third line vanishes because at the end points. Finally, according to the fundamental lemma of calculus of variations
at the end points. Finally, according to the fundamental lemma of calculus of variations
, we find that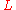 will satisfy the Euler–Lagrange equation
will satisfy the Euler–Lagrange equation
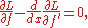
In general this gives a second-order ordinary differential equation
which can be solved to obtain the extremal . The Euler–Lagrange equation is a necessary, but not sufficient, condition for an extremal. Sufficient conditions for an extremal are discussed in the references.
. The Euler–Lagrange equation is a necessary, but not sufficient, condition for an extremal. Sufficient conditions for an extremal are discussed in the references.
In order to illustrate this process, consider the problem of finding the shortest curve in the plane that connects two points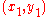 and
and 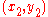 . The arc length
. The arc length
is given by

with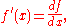
and where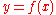 ,
, 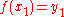 , and
, and 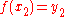 .
.
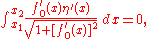
for any choice of the function . We may interpret this condition as the vanishing of all directional derivative
. We may interpret this condition as the vanishing of all directional derivative
s of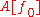 in the space of differentiable functions, and this is formalized by requiring the Fréchet derivative
in the space of differentiable functions, and this is formalized by requiring the Fréchet derivative
of to vanish at
to vanish at 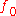 . If we assume that
. If we assume that  has two continuous derivatives (or if we consider weak derivative
has two continuous derivatives (or if we consider weak derivative
s), then we may use integration by parts
:

with the substitution
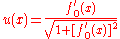
then we have
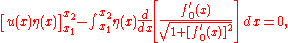
but the first term is zero since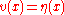 was chosen to vanish at
was chosen to vanish at 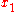 and
and 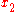 where the evaluation is taken. Therefore,
where the evaluation is taken. Therefore,
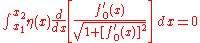
for any twice differentiable function that vanishes at the endpoints of the interval.
that vanishes at the endpoints of the interval.
We can now apply the fundamental lemma of calculus of variations
: If

for any sufficiently differentiable function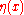 within the integration range that vanishes at the endpoints of the interval, then it follows that
within the integration range that vanishes at the endpoints of the interval, then it follows that 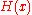 is identically zero on its domain.
is identically zero on its domain.
Therefore,

It follows from this equation that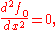
and hence the extremals are straight lines.
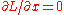 . In that case, the Euler-Lagrange equation can be simplified using the Beltrami identity
. In that case, the Euler-Lagrange equation can be simplified using the Beltrami identity
:
 http://planetmath.org/encyclopedia/BeltramiIdentity.html
http://planetmath.org/encyclopedia/BeltramiIdentity.html
where is a constant. The left hand side is the Legendre transformation
is a constant. The left hand side is the Legendre transformation
of L with respect to f '.
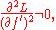
then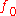 has two continuous derivatives, and it satisfies the Euler-Lagrange equation.
has two continuous derivatives, and it satisfies the Euler-Lagrange equation.
However Lavrentiev
in 1926 showed that there are circumstances where there is no optimum solution but one can be approached arbitrarily closely by increasing numbers of sections. For instance the following:
Here a zig zag path gives a better solution than any smooth path and increasing the number of sections improves the solution.

Plateau's problem
consists of finding a function that minimizes the surface area while assuming prescribed values on the boundary of D; the solutions are called minimal surfaces. The Euler-Lagrange equation for this problem is nonlinear: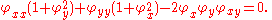
See Courant (1950) for details.
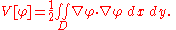
The functional V is to be minimized among all trial functions φ that assume prescribed values on the boundary of D. If u is the minimizing function and v is an arbitrary smooth function that vanishes on the boundary of D, then the first variation of must vanish:
must vanish:
Provided that u has two derivatives, we may apply the divergence theorem to obtain
where C is the boundary of D, s is arclength along C and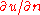 is the normal derivative of u on C. Since v vanishes on C and the first variation vanishes, the result is
is the normal derivative of u on C. Since v vanishes on C and the first variation vanishes, the result is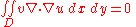
for all smooth functions v that vanish on the boundary of D. The proof for the case of one dimensional integrals may be adapted to this case to show that in D.
in D.
The difficulty with this reasoning is the assumption that the minimizing function u must have two derivatives. Riemann argued that the existence of a smooth minimizing function was assured by the connection with the physical problem: membranes do indeed assume configurations with minimal potential energy. Riemann named this idea the Dirichlet principle in honor of his teacher Dirichlet. However Weierstrass gave an example of a variational problem with no solution: minimize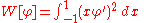
among all functions φ that satisfy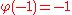 and
and
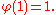
W can be made arbitrarily small by choosing piecewise linear functions that
make a transition between -1 and 1 in a small neighborhood of the origin. However, there is no function that makes W=0. The resulting controversy over the validity of Dirichlet's principle is explained in
http://turnbull.mcs.st-and.ac.uk/~history/Biographies/Riemann.html .
Eventually it was shown that Dirichlet's principle is valid, but it requires a sophisticated application of the regularity theory for elliptic partial differential equations; see Jost and Li-Jost (1998).
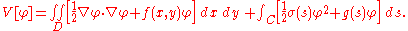
This corresponds to an external force density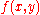 in D, an external force
in D, an external force  on the boundary C, and elastic forces with modulus
on the boundary C, and elastic forces with modulus 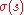 acting on C. The function that minimizes the potential energy with no restriction on its boundary values will be denoted by u. Provided that f and g are continuous, regularity theory implies that the minimizing function u will have two derivatives. In taking the first variation, no boundary condition need be imposed on the increment v. The first variation of
acting on C. The function that minimizes the potential energy with no restriction on its boundary values will be denoted by u. Provided that f and g are continuous, regularity theory implies that the minimizing function u will have two derivatives. In taking the first variation, no boundary condition need be imposed on the increment v. The first variation of
 is given by
is given by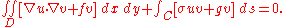
If we apply the divergence theorem, the result is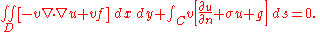
If we first set v=0 on C, the boundary integral vanishes, and we conclude as before that
in D. Then if we allow v to assume arbitrary boundary values, this implies that u must satisfy the boundary condition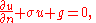
on C. Note that this boundary condition is a consequence of the minimizing property of u: it is not imposed beforehand. Such conditions are called natural boundary conditions.
The preceding reasoning is not valid if vanishes identically on C. In such a case, we could allow a trial function
vanishes identically on C. In such a case, we could allow a trial function
 , where c is a constant. For such a trial function,
, where c is a constant. For such a trial function,
By appropriate choice of c, V can assume any value unless the quantity inside the brackets vanishes. Therefore the variational problem is meaningless unless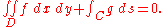
This condition implies that net external forces on the system are in equilibrium. If these forces are in equilibrium, then the variational problem has a solution, but it is not unique, since an arbitrary constant may be added. Further details and examples are in Courant and Hilbert (1953).
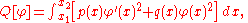
where φ is restricted to functions that satisfy the boundary conditions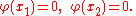
Let R be a normalization integral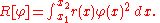
The functions and
and 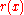 are required to be everywhere positive and bounded away from zero. The primary variational problem is to minimize the ratio Q/R among all φ satisfying the endpoint conditions. It is shown below that the Euler-Lagrange equation for the minimizing u is
are required to be everywhere positive and bounded away from zero. The primary variational problem is to minimize the ratio Q/R among all φ satisfying the endpoint conditions. It is shown below that the Euler-Lagrange equation for the minimizing u is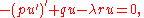
where λ is the quotient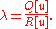
It can be shown (see Gelfand and Fomin 1963) that the minimizing u has two derivatives and satisfies the Euler-Lagrange equation. The associated λ will be denoted by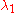 ; it is the lowest eigenvalue for this equation and boundary conditions. The associated minimizing function will be denoted by
; it is the lowest eigenvalue for this equation and boundary conditions. The associated minimizing function will be denoted by 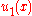 . This variational characterization of eigenvalues leads to the Rayleigh-Ritz method: choose an approximating u as a linear combination of basis functions (for example trigonometric functions) and carry out a finite-dimensional minimization among such linear combinations. This method is often surprisingly accurate.
. This variational characterization of eigenvalues leads to the Rayleigh-Ritz method: choose an approximating u as a linear combination of basis functions (for example trigonometric functions) and carry out a finite-dimensional minimization among such linear combinations. This method is often surprisingly accurate.
The next smallest eigenvalue and eigenfunction can be obtained by minimizing Q under the additional constraint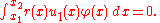
This procedure can be extended to obtain the complete sequence of eigenvalues and eigenfunctions for the problem.
The variational problem also applies to more general boundary conditions. Instead of requiring that φ vanish at the endpoints, we may not impose any condition at the endpoints, and set
where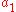 and
and 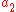 are arbitrary. If we set
are arbitrary. If we set 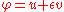 the first variation for the ratio
the first variation for the ratio 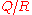 is
is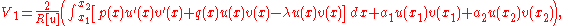
where λ is given by the ratio as previously.
as previously.
After integration by parts,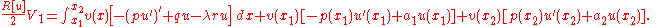
If we first require that v vanish at the endpoints, the first variation will vanish for all such v only if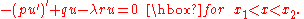
If u satisfies this condition, then the first variation will vanish for arbitrary v only if
These latter conditions are the natural boundary conditions for this problem, since they are not imposed on trial functions for the minimization, but are instead a consequence of the minimization.
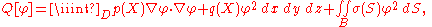
and
Let u be the function that minimizes the quotient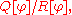
with no condition prescribed on the boundary B. The Euler-Lagrange equation satisfied by u is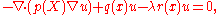
where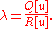
The minimizing u must also satisfy the natural boundary condition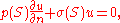
on the boundary B. This result depends upon the regularity theory for elliptic partial differential equations; see Jost and Li-Jost (1998) for details. Many extensions, including completeness results, asymptotic properties of the eigenvalues and results concerning the nodes of the eigenfunctions are in Courant and Hilbert (1953).
states that light takes a path that (locally) minimizes the optical length between its endpoints. If the x-coordinate is chosen as the parameter along the path, and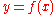 along the path, then the optical length is given by
along the path, then the optical length is given by

where the refractive index depends upon the material.
depends upon the material.
If we try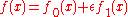
then the first variation
of A (the derivative of A with respect to ε) is

After integration by parts of the first term within brackets, we obtain the Euler-Lagrange equation

The light rays may be determined by integrating this equation. This formalism is used in the context of Lagrangian optics and Hamiltonian optics
.
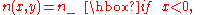

where and
and  are constants. Then the Euler-Lagrange equation holds as before in the region where x<0 or x>0, and in fact the path is a straight line there, since the refractive index is constant. At the x=0, f must be continuous, but f' may be discontinuous. After integration by parts in the separate regions and using the Euler-Lagrange equations, the first variation takes the form
are constants. Then the Euler-Lagrange equation holds as before in the region where x<0 or x>0, and in fact the path is a straight line there, since the refractive index is constant. At the x=0, f must be continuous, but f' may be discontinuous. After integration by parts in the separate regions and using the Euler-Lagrange equations, the first variation takes the form

The factor multiplying is the sine of angle of the incident ray with the x axis, and the factor multiplying
is the sine of angle of the incident ray with the x axis, and the factor multiplying  is the sine of angle of the refracted ray with the x axis. Snell's law
is the sine of angle of the refracted ray with the x axis. Snell's law
for refraction requires that these terms be equal. As this calculation demonstrates, Snell's law is equivalent to vanishing of the first variation of the optical path length.
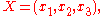 let t be a parameter, let
let t be a parameter, let 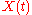 be the parametric representation of a curve C, and let
be the parametric representation of a curve C, and let  be its tangent vector. The optical length of the curve is given by
be its tangent vector. The optical length of the curve is given by
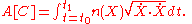
Note that this integral is invariant with respect to changes in the parametric representation of C. The Euler-Lagrange equations for a minimizing curve have the symmetric form
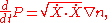
where
It follows from the definition that P satisfies
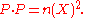
Therefore the integral may also be written as
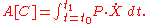
This form suggests that if we can find a function ψ whose gradient is given by P, then the integral A is given by the difference of ψ at the endpoints of the interval of integration. Thus the problem of studying the curves that make the integral stationary can be related to the study of the level surfaces of ψ. In order to find such a function, we turn to the wave equation, which governs the propagation of light. This formalism is used in the context of Lagrangian optics and Hamiltonian optics
.
The wave equation
for an inhomogeneous medium is
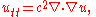
where c is the velocity, which generally depends upon X. Wave fronts for light are characteristic surfaces for this partial differential equation: they satisfy
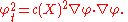
We may look for solutions in the form

In that case, ψ satisfies

where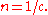 According to the theory of first-order partial differential equations, if
According to the theory of first-order partial differential equations, if  then P satisfies
then P satisfies

along a system of curves (the light rays) that are given by
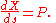
These equations for solution of a first-order partial differential equation are identical to the Euler-Lagrange equations if we make the identification
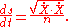
We conclude that the function ψ is the value of the minimizing integral A as a function of the upper end point. That is, when a family of minimizing curves is constructed, the values of the optical length satisfy the characteristic equation corresponding the wave equation. Hence, solving the associated partial differential equation of first order is equivalent to finding families of solutions of the variational problem. This is the essential content of the Hamilton-Jacobi theory, which applies to more general variational problems.
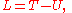
where T is the kinetic energy of a mechanical system and U its potential energy. Hamilton's principle
(or the action principle) states that the motion of a conservative holonomic (integrable constraints) mechanical system is such that the action integral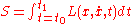
is stationary with respect to variations in the path x(t).
The Euler-Lagrange equations for this system are known as Lagrange's equations: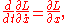
and they are equivalent to Newton's equations of motion (for such systems).
The conjugate momenta P are defined by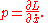
For example, if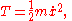
then
Hamiltonian mechanics
results if the conjugate momenta are introduced in place of , and the Lagrangian L is replaced by the Hamiltonian H defined by
, and the Lagrangian L is replaced by the Hamiltonian H defined by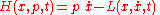
The Hamiltonian is the total energy of the system: H = T + U.
Analogy with Fermat's principle suggests that solutions of Lagrange's equations (the particle trajectories) may be described in terms of level surfaces of some function of X. This function is a solution of the Hamilton-Jacobi equation: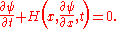
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
that deals with extremizing functionals
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
, as opposed to ordinary calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
which deals with functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown functions and their derivatives. The interest is in extremal functions that make the functional attain a maximum or minimum value – or stationary functions – those where the rate of change of the functional is precisely zero.
Perhaps the simplest example of such a problem is to find the curve of shortest length, or geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
, connecting two points. If there are no constraints, the solution is obviously a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. A related problem is posed by Fermat's principle
Fermat's principle
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
: light follows the path of shortest optical length connecting two points, where the optical length depends upon the material of the medium. One corresponding concept in mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
is the principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
.
Many important problems involve functions of several variables. Solutions of boundary value problems for the Laplace equation satisfy the Dirichlet principle. Plateau's problem
Plateau's problem
In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who was interested in soap films. The problem is considered part of the calculus of variations...
requires finding a surface of minimal area that spans a given contour in space: the solution or solutions can often be found by dipping a wire frame in a solution of soap suds. Although such experiments are relatively easy to perform, their mathematical interpretation is far from simple: there may be more than one locally minimizing surface, and they may have non-trivial topology.
History
The calculus of variations may be said to begin with the brachistochrone curveBrachistochrone curve
A Brachistochrone curve , or curve of fastest descent, is the curve between two points that is covered in the least time by a point-like body that starts at the first point with zero speed and is constrained to move along the curve to the second point, under the action of constant gravity and...
problem raised by Johann Bernoulli
Johann Bernoulli
Johann Bernoulli was a Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family...
(1696). It immediately occupied the attention of Jakob Bernoulli and the Marquis de l'Hôpital
Guillaume de l'Hôpital
Guillaume François Antoine, Marquis de l'Hôpital was a French mathematician. His name is firmly associated with l'Hôpital's rule for calculating limits involving indeterminate forms 0/0 and ∞/∞...
, but Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
first elaborated the subject. His contributions began in 1733, and his Elementa Calculi Variationum gave to the science its name. Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
contributed extensively to the theory, and Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
(1786) laid down a method, not entirely satisfactory, for the discrimination of maxima and minima. Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
also gave some early attention to the subject. To this discrimination Vincenzo Brunacci (1810), Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
(1829), Siméon Poisson (1831), Mikhail Ostrogradsky (1834), and Carl Jacobi
Carl Gustav Jakob Jacobi
Carl Gustav Jacob Jacobi was a German mathematician, widely considered to be the most inspiring teacher of his time and is considered one of the greatest mathematicians of his generation.-Biography:...
(1837) have been among the contributors. An important general work is that of Sarrus
Sarrus
Sarrus is the last name of :* Pierre-Auguste Sarrus , French musician and inventor* Pierre Frédéric Sarrus , French mathematicianSarrus may also refer to:...
(1842) which was condensed and improved by Cauchy (1844). Other valuable treatises and memoirs have been written by Strauch
Strauch
Strauch, a German word meaning bush or shrub, may refer to :* Adolfo Strauch, a survivor of the Uruguayan Air Force Flight 571 crash* Adolph Strauch , a renowned landscape architect* Alexander Strauch , multiple people...
(1849), Jellett (1850), Otto Hesse
Otto Hesse
Ludwig Otto Hesse was a German mathematician. Hesse was born in Königsberg, Prussia, and died in Munich, Bavaria. He worked on algebraic invariants...
(1857), Alfred Clebsch
Alfred Clebsch
Rudolf Friedrich Alfred Clebsch was a German mathematician who made important contributions to algebraic geometry and invariant theory. He attended the University of Königsberg and was habilitated at Berlin. He subsequently taught in Berlin and Karlsruhe...
(1858), and Carll (1885), but perhaps the most important work of the century is that of Weierstrass. His celebrated course on the theory is epoch-making, and it may be asserted that he was the first to place it on a firm and unquestionable foundation. The 20th
Hilbert's twentieth problem
Hilbert's twentieth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. It asks whether all boundary value problems can be solved...
and the 23rd
Hilbert's twenty-third problem
Hilbert's twenty-third problem is the last of Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert. In contrast with Hilbert's other 22 problems, his 23rd is not so much a specific "problem" as an encouragement towards further development of the calculus of variations...
Hilbert problems published in 1900 enticed further development. In the 20th century David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, Emmy Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
, Leonida Tonelli
Leonida Tonelli
Leonida Tonelli was an Italian mathematician, most noted for creating Tonelli's theorem, usually considered a forerunner to Fubini's theorem.-External links:...
, Henri Lebesgue
Henri Lebesgue
Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...
and Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
among others made significant contributions. Marston Morse
Marston Morse
Harold Calvin Marston Morse was an American mathematician best known for his work on the calculus of variations in the large, a subject where he introduced the technique of differential topology now known as Morse theory...
applied calculus of variations in what is now called Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
. Lev Pontryagin, Ralph Rockafellar
R. Tyrrell Rockafellar
* for the George Dantzig Prize in 1994 in Optima, Issue 44 page 5.- Books :* Rockafellar, R. Tyrrell. Conjugate duality and optimization. Lectures given at the Johns Hopkins University, Baltimore, Md., June, 1973. Conference Board of the Mathematical Sciences Regional Conference Series in Applied...
and Clarke
Clarke
Clarke is a common surname, being the 20th most common surname in England as of 2008. Clarke is an English surname and is a variant of Clark, Clerk or Clerke; the word deriving from the Old English word 'clerc' for a cleric or scribe. It is from a medieval occupational name for a scribe or...
developed new mathematical tools for optimal control theory, a generalisation of calculus of variations.
Weak and strong extrema
The supremum norm (also called infinity norm) for real, continuous, bounded functions on a topological space is defined as
is defined as
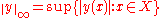 .
.
A functional
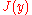 defined on some appropriate space of functions
defined on some appropriate space of functions  with norm
with norm 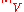 is said to have a weak minimum at the function
is said to have a weak minimum at the function 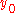 if there exists some
if there exists some  such that, for all functions y with
such that, for all functions y with 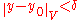 ,
,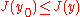 .
.Weak maxima are defined similarly, with the inequality in the last equation reversed. In most problems,
 is the space of r-times continuously differentiable functions on a compact subset
is the space of r-times continuously differentiable functions on a compact subset  of the real line, with its norm given by
of the real line, with its norm given by .
.This norm is just the sum of the supremum norms of
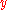 and its derivatives.
and its derivatives.A functional
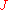 is said to have a strong minimum at
is said to have a strong minimum at  if there exists some
if there exists some  such that, for all functions
such that, for all functions 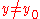 with
with 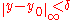 ,
,  . Strong maximum is defined similarly, but with the inequality in the last equation reversed.
. Strong maximum is defined similarly, but with the inequality in the last equation reversed.The difference between strong and weak extrema is that, for a strong extremum,
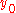 is a local extremum relative to the set of
is a local extremum relative to the set of  -close functions with respect to the supremum norm. In general this (supremum) norm is different from the norm
-close functions with respect to the supremum norm. In general this (supremum) norm is different from the norm 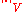 that V has been endowed with. If
that V has been endowed with. If 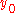 is a strong extremum for
is a strong extremum for 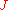 then it is also a weak extremum, but the converse may not hold. Finding strong extrema is more difficult than finding weak extrema and in what follows it will be assumed that we are looking for weak extrema.
then it is also a weak extremum, but the converse may not hold. Finding strong extrema is more difficult than finding weak extrema and in what follows it will be assumed that we are looking for weak extrema.The Euler–Lagrange equation
Under ideal conditions, the maxima and minima of a given function may be located by finding the points where its derivative vanishes (i.e., is equal to zero). By analogy, solutions of smooth variational problems may be obtained by solving the associated Euler–Lagrange equation.Consider the functional:
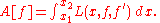
The function
 should have at least one derivative in order to satisfy the requirements for valid application of the function; further, if the functional
should have at least one derivative in order to satisfy the requirements for valid application of the function; further, if the functional 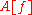 attains its local minimum at
attains its local minimum at 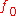 and
and 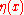 is an arbitrary function that has at least one derivative and vanishes at the endpoints
is an arbitrary function that has at least one derivative and vanishes at the endpoints 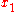 and
and  , then we must have
, then we must have
for any number ε close to 0. Therefore, the derivative of
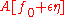 with respect to ε (the first variation
with respect to ε (the first variationFirst variation
In applied mathematics and the calculus of variations, the first variation of a functional J is defined as the linear functional \delta J mapping the function h to...
of A) must vanish at ε = 0.
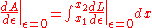
Since
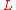 is a function of
is a function of  and
and 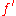 , the term
, the term
with
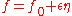 . Therefore,
. Therefore,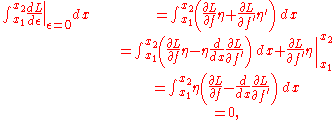
where we have used the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
in the second line and integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
in the third. The last term in the third line vanishes because
 at the end points. Finally, according to the fundamental lemma of calculus of variations
at the end points. Finally, according to the fundamental lemma of calculus of variationsFundamental lemma of calculus of variations
In mathematics, specifically in the calculus of variations, the fundamental lemma in the calculus of variations is a lemma that is typically used to transform a problem from its weak formulation into its strong formulation .-Statement:A function is said to be of class C^k if it is k-times...
, we find that
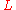 will satisfy the Euler–Lagrange equation
will satisfy the Euler–Lagrange equation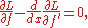
In general this gives a second-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
which can be solved to obtain the extremal
 . The Euler–Lagrange equation is a necessary, but not sufficient, condition for an extremal. Sufficient conditions for an extremal are discussed in the references.
. The Euler–Lagrange equation is a necessary, but not sufficient, condition for an extremal. Sufficient conditions for an extremal are discussed in the references.In order to illustrate this process, consider the problem of finding the shortest curve in the plane that connects two points
 and
and 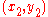 . The arc length
. The arc lengthArc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
is given by

with
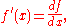
and where
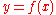 ,
, 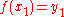 , and
, and 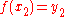 .
.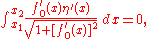
for any choice of the function
 . We may interpret this condition as the vanishing of all directional derivative
. We may interpret this condition as the vanishing of all directional derivativeDirectional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
s of
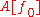 in the space of differentiable functions, and this is formalized by requiring the Fréchet derivative
in the space of differentiable functions, and this is formalized by requiring the Fréchet derivativeFréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
of
 to vanish at
to vanish at 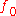 . If we assume that
. If we assume that  has two continuous derivatives (or if we consider weak derivative
has two continuous derivatives (or if we consider weak derivativeWeak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
s), then we may use integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
:

with the substitution
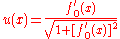
then we have
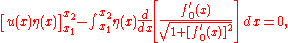
but the first term is zero since
 was chosen to vanish at
was chosen to vanish at  and
and 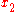 where the evaluation is taken. Therefore,
where the evaluation is taken. Therefore,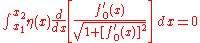
for any twice differentiable function
 that vanishes at the endpoints of the interval.
that vanishes at the endpoints of the interval.We can now apply the fundamental lemma of calculus of variations
Fundamental lemma of calculus of variations
In mathematics, specifically in the calculus of variations, the fundamental lemma in the calculus of variations is a lemma that is typically used to transform a problem from its weak formulation into its strong formulation .-Statement:A function is said to be of class C^k if it is k-times...
: If

for any sufficiently differentiable function
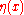 within the integration range that vanishes at the endpoints of the interval, then it follows that
within the integration range that vanishes at the endpoints of the interval, then it follows that 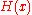 is identically zero on its domain.
is identically zero on its domain.Therefore,

It follows from this equation that
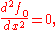
and hence the extremals are straight lines.
The Beltrami Identity
Frequently in physical problems, it turns out that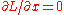 . In that case, the Euler-Lagrange equation can be simplified using the Beltrami identity
. In that case, the Euler-Lagrange equation can be simplified using the Beltrami identityBeltrami identity
The Beltrami identity is an identity in the calculus of variations. It says that a function u which is an extremal of the integralI=\int_a^b L \, dxsatisfies the differential equation...
:
 http://planetmath.org/encyclopedia/BeltramiIdentity.html
http://planetmath.org/encyclopedia/BeltramiIdentity.htmlwhere
 is a constant. The left hand side is the Legendre transformation
is a constant. The left hand side is the Legendre transformationLegendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
of L with respect to f '.
du Bois Reymond's theorem
The discussion thus far has assumed that extremal functions possess two continuous derivatives, although the existence of the integral A requires only first derivatives of trial functions. The condition that the first variation vanish at an extremal may be regarded as a weak form of the Euler-Lagrange equation. The theorem of du Bois Reymond asserts that this weak form implies the strong form. If L has continuous first and second derivatives with respect to all of its arguments, and if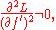
then
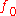 has two continuous derivatives, and it satisfies the Euler-Lagrange equation.
has two continuous derivatives, and it satisfies the Euler-Lagrange equation.The Lavrentiev phenomenon
Hilbert was the first to give good conditions for the Euler Lagrange equations to give a stationary solution. Within a convex area and a positive thrice differentiable Lagrangian the solutions are composed of a countable collection of sections that either go along the boundary or satisfy the Euler Lagrange equations in the interior.However Lavrentiev
Mikhail Lavrentyev
Mikhail Alekseevich Lavrentyev or Lavrentiev was an outstanding Soviet mathematician and hydrodynamicist.-Biography:...
in 1926 showed that there are circumstances where there is no optimum solution but one can be approached arbitrarily closely by increasing numbers of sections. For instance the following:

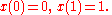
Here a zig zag path gives a better solution than any smooth path and increasing the number of sections improves the solution.
Functions of several variables
Variational problems that involve multiple integrals arise in numerous applications. For example, if φ(x,y) denotes the displacement of a membrane above the domain D in the x,y plane, then its potential energy is proportional to its surface area:
Plateau's problem
Plateau's problem
In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who was interested in soap films. The problem is considered part of the calculus of variations...
consists of finding a function that minimizes the surface area while assuming prescribed values on the boundary of D; the solutions are called minimal surfaces. The Euler-Lagrange equation for this problem is nonlinear:
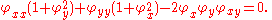
See Courant (1950) for details.
Dirichlet's principle
It is often sufficient to consider only small displacements of the membrane, whose energy difference from no displacement is approximated by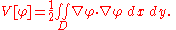
The functional V is to be minimized among all trial functions φ that assume prescribed values on the boundary of D. If u is the minimizing function and v is an arbitrary smooth function that vanishes on the boundary of D, then the first variation of
 must vanish:
must vanish:
Provided that u has two derivatives, we may apply the divergence theorem to obtain

where C is the boundary of D, s is arclength along C and
 is the normal derivative of u on C. Since v vanishes on C and the first variation vanishes, the result is
is the normal derivative of u on C. Since v vanishes on C and the first variation vanishes, the result is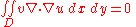
for all smooth functions v that vanish on the boundary of D. The proof for the case of one dimensional integrals may be adapted to this case to show that
 in D.
in D.The difficulty with this reasoning is the assumption that the minimizing function u must have two derivatives. Riemann argued that the existence of a smooth minimizing function was assured by the connection with the physical problem: membranes do indeed assume configurations with minimal potential energy. Riemann named this idea the Dirichlet principle in honor of his teacher Dirichlet. However Weierstrass gave an example of a variational problem with no solution: minimize
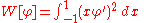
among all functions φ that satisfy
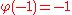 and
and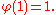
W can be made arbitrarily small by choosing piecewise linear functions that
make a transition between -1 and 1 in a small neighborhood of the origin. However, there is no function that makes W=0. The resulting controversy over the validity of Dirichlet's principle is explained in
http://turnbull.mcs.st-and.ac.uk/~history/Biographies/Riemann.html .
Eventually it was shown that Dirichlet's principle is valid, but it requires a sophisticated application of the regularity theory for elliptic partial differential equations; see Jost and Li-Jost (1998).
Generalization to other boundary value problems
A more general expression for the potential energy of a membrane is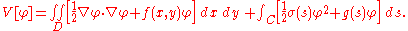
This corresponds to an external force density
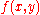 in D, an external force
in D, an external force  on the boundary C, and elastic forces with modulus
on the boundary C, and elastic forces with modulus 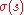 acting on C. The function that minimizes the potential energy with no restriction on its boundary values will be denoted by u. Provided that f and g are continuous, regularity theory implies that the minimizing function u will have two derivatives. In taking the first variation, no boundary condition need be imposed on the increment v. The first variation of
acting on C. The function that minimizes the potential energy with no restriction on its boundary values will be denoted by u. Provided that f and g are continuous, regularity theory implies that the minimizing function u will have two derivatives. In taking the first variation, no boundary condition need be imposed on the increment v. The first variation of is given by
is given by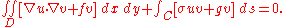
If we apply the divergence theorem, the result is
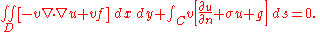
If we first set v=0 on C, the boundary integral vanishes, and we conclude as before that

in D. Then if we allow v to assume arbitrary boundary values, this implies that u must satisfy the boundary condition
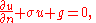
on C. Note that this boundary condition is a consequence of the minimizing property of u: it is not imposed beforehand. Such conditions are called natural boundary conditions.
The preceding reasoning is not valid if
 vanishes identically on C. In such a case, we could allow a trial function
vanishes identically on C. In such a case, we could allow a trial function , where c is a constant. For such a trial function,
, where c is a constant. For such a trial function,
By appropriate choice of c, V can assume any value unless the quantity inside the brackets vanishes. Therefore the variational problem is meaningless unless
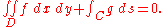
This condition implies that net external forces on the system are in equilibrium. If these forces are in equilibrium, then the variational problem has a solution, but it is not unique, since an arbitrary constant may be added. Further details and examples are in Courant and Hilbert (1953).
Eigenvalue problems
Both one-dimensional and multi-dimensional eigenvalue problems can be formulated as variational problems.Sturm-Liouville problems
The Sturm-Liouville eigenvalue problem involves a general quadratic form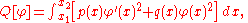
where φ is restricted to functions that satisfy the boundary conditions
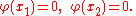
Let R be a normalization integral
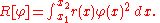
The functions
 and
and 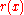 are required to be everywhere positive and bounded away from zero. The primary variational problem is to minimize the ratio Q/R among all φ satisfying the endpoint conditions. It is shown below that the Euler-Lagrange equation for the minimizing u is
are required to be everywhere positive and bounded away from zero. The primary variational problem is to minimize the ratio Q/R among all φ satisfying the endpoint conditions. It is shown below that the Euler-Lagrange equation for the minimizing u is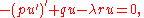
where λ is the quotient
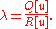
It can be shown (see Gelfand and Fomin 1963) that the minimizing u has two derivatives and satisfies the Euler-Lagrange equation. The associated λ will be denoted by
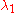 ; it is the lowest eigenvalue for this equation and boundary conditions. The associated minimizing function will be denoted by
; it is the lowest eigenvalue for this equation and boundary conditions. The associated minimizing function will be denoted by 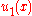 . This variational characterization of eigenvalues leads to the Rayleigh-Ritz method: choose an approximating u as a linear combination of basis functions (for example trigonometric functions) and carry out a finite-dimensional minimization among such linear combinations. This method is often surprisingly accurate.
. This variational characterization of eigenvalues leads to the Rayleigh-Ritz method: choose an approximating u as a linear combination of basis functions (for example trigonometric functions) and carry out a finite-dimensional minimization among such linear combinations. This method is often surprisingly accurate.The next smallest eigenvalue and eigenfunction can be obtained by minimizing Q under the additional constraint
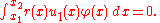
This procedure can be extended to obtain the complete sequence of eigenvalues and eigenfunctions for the problem.
The variational problem also applies to more general boundary conditions. Instead of requiring that φ vanish at the endpoints, we may not impose any condition at the endpoints, and set

where
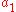 and
and 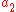 are arbitrary. If we set
are arbitrary. If we set 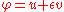 the first variation for the ratio
the first variation for the ratio 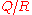 is
is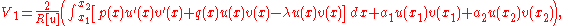
where λ is given by the ratio
 as previously.
as previously.After integration by parts,
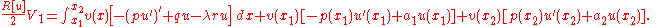
If we first require that v vanish at the endpoints, the first variation will vanish for all such v only if
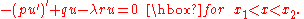
If u satisfies this condition, then the first variation will vanish for arbitrary v only if

These latter conditions are the natural boundary conditions for this problem, since they are not imposed on trial functions for the minimization, but are instead a consequence of the minimization.
Eigenvalue problems in several dimensions
Eigenvalue problems in higher dimensions are defined in analogy with the one-dimensional case. For example, given a domain D with boundary B in three dimensions we may define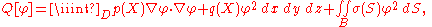
and

Let u be the function that minimizes the quotient
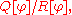
with no condition prescribed on the boundary B. The Euler-Lagrange equation satisfied by u is
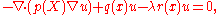
where
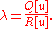
The minimizing u must also satisfy the natural boundary condition
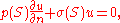
on the boundary B. This result depends upon the regularity theory for elliptic partial differential equations; see Jost and Li-Jost (1998) for details. Many extensions, including completeness results, asymptotic properties of the eigenvalues and results concerning the nodes of the eigenfunctions are in Courant and Hilbert (1953).
Applications
Some applications of the Calculus of variations include:- The derivation of the CatenaryCatenaryIn physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
shape - The BrachistochroneBrachistochrone curveA Brachistochrone curve , or curve of fastest descent, is the curve between two points that is covered in the least time by a point-like body that starts at the first point with zero speed and is constrained to move along the curve to the second point, under the action of constant gravity and...
problem - Isoperimetric problems
- Geodesics on surfaces
- Minimal surfaces and Plateau's problemPlateau's problemIn mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who was interested in soap films. The problem is considered part of the calculus of variations...
- Optimal ControlOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
Fermat's principle
Fermat's principleFermat's principle
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
states that light takes a path that (locally) minimizes the optical length between its endpoints. If the x-coordinate is chosen as the parameter along the path, and
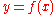 along the path, then the optical length is given by
along the path, then the optical length is given by
where the refractive index
 depends upon the material.
depends upon the material.If we try
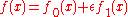
then the first variation
First variation
In applied mathematics and the calculus of variations, the first variation of a functional J is defined as the linear functional \delta J mapping the function h to...
of A (the derivative of A with respect to ε) is

After integration by parts of the first term within brackets, we obtain the Euler-Lagrange equation

The light rays may be determined by integrating this equation. This formalism is used in the context of Lagrangian optics and Hamiltonian optics
Hamiltonian optics
Lagrangian optics and Hamiltonian optics are two formulations of geometrical optics which share much of the mathematical formalism with Lagrangian mechanics and Hamiltonian mechanics.-Hamilton's principle:...
.
Snell's law
There is a discontinuity of the refractive index when light enters or leaves a lens. Let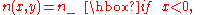

where
 and
and  are constants. Then the Euler-Lagrange equation holds as before in the region where x<0 or x>0, and in fact the path is a straight line there, since the refractive index is constant. At the x=0, f must be continuous, but f' may be discontinuous. After integration by parts in the separate regions and using the Euler-Lagrange equations, the first variation takes the form
are constants. Then the Euler-Lagrange equation holds as before in the region where x<0 or x>0, and in fact the path is a straight line there, since the refractive index is constant. At the x=0, f must be continuous, but f' may be discontinuous. After integration by parts in the separate regions and using the Euler-Lagrange equations, the first variation takes the form
The factor multiplying
 is the sine of angle of the incident ray with the x axis, and the factor multiplying
is the sine of angle of the incident ray with the x axis, and the factor multiplying  is the sine of angle of the refracted ray with the x axis. Snell's law
is the sine of angle of the refracted ray with the x axis. Snell's lawSnell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
for refraction requires that these terms be equal. As this calculation demonstrates, Snell's law is equivalent to vanishing of the first variation of the optical path length.
Fermat's principle in three dimensions
It is expedient to use vector notation: let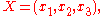 let t be a parameter, let
let t be a parameter, let 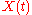 be the parametric representation of a curve C, and let
be the parametric representation of a curve C, and let  be its tangent vector. The optical length of the curve is given by
be its tangent vector. The optical length of the curve is given by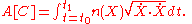
Note that this integral is invariant with respect to changes in the parametric representation of C. The Euler-Lagrange equations for a minimizing curve have the symmetric form
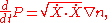
where

It follows from the definition that P satisfies
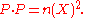
Therefore the integral may also be written as
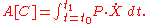
This form suggests that if we can find a function ψ whose gradient is given by P, then the integral A is given by the difference of ψ at the endpoints of the interval of integration. Thus the problem of studying the curves that make the integral stationary can be related to the study of the level surfaces of ψ. In order to find such a function, we turn to the wave equation, which governs the propagation of light. This formalism is used in the context of Lagrangian optics and Hamiltonian optics
Hamiltonian optics
Lagrangian optics and Hamiltonian optics are two formulations of geometrical optics which share much of the mathematical formalism with Lagrangian mechanics and Hamiltonian mechanics.-Hamilton's principle:...
.
Connection with the wave equation
The wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
for an inhomogeneous medium is
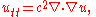
where c is the velocity, which generally depends upon X. Wave fronts for light are characteristic surfaces for this partial differential equation: they satisfy
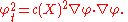
We may look for solutions in the form

In that case, ψ satisfies

where
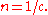 According to the theory of first-order partial differential equations, if
According to the theory of first-order partial differential equations, if  then P satisfies
then P satisfies
along a system of curves (the light rays) that are given by
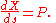
These equations for solution of a first-order partial differential equation are identical to the Euler-Lagrange equations if we make the identification
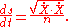
We conclude that the function ψ is the value of the minimizing integral A as a function of the upper end point. That is, when a family of minimizing curves is constructed, the values of the optical length satisfy the characteristic equation corresponding the wave equation. Hence, solving the associated partial differential equation of first order is equivalent to finding families of solutions of the variational problem. This is the essential content of the Hamilton-Jacobi theory, which applies to more general variational problems.
The action principle
In classical mechanics, the action, S, is defined as the time integral of the Lagrangian, L. The Lagrangian is the difference of energies,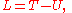
where T is the kinetic energy of a mechanical system and U its potential energy. Hamilton's principle
Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
(or the action principle) states that the motion of a conservative holonomic (integrable constraints) mechanical system is such that the action integral
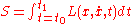
is stationary with respect to variations in the path x(t).
The Euler-Lagrange equations for this system are known as Lagrange's equations:
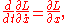
and they are equivalent to Newton's equations of motion (for such systems).
The conjugate momenta P are defined by
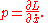
For example, if
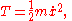
then

Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
results if the conjugate momenta are introduced in place of
 , and the Lagrangian L is replaced by the Hamiltonian H defined by
, and the Lagrangian L is replaced by the Hamiltonian H defined by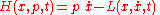
The Hamiltonian is the total energy of the system: H = T + U.
Analogy with Fermat's principle suggests that solutions of Lagrange's equations (the particle trajectories) may be described in terms of level surfaces of some function of X. This function is a solution of the Hamilton-Jacobi equation:
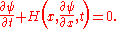
See also
- First variationFirst variationIn applied mathematics and the calculus of variations, the first variation of a functional J is defined as the linear functional \delta J mapping the function h to...
- Isoperimetric inequality
- Variational principleVariational principleA variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
- Fermat's principleFermat's principleIn optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
- Principle of least actionPrinciple of least actionIn physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
- Infinite-dimensional optimizationInfinite-dimensional optimizationIn certain optimization problems the unknown optimal solution might not be a number or a vector, but rather a continuous quantity, for example a function or the shape of a body...
- Functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
- Perturbation methods
- Young measureYoung measureIn mathematical analysis, a Young measure is a parameterized measure that is associated with certain subsequences of a given bounded sequence of measurable functions. Young measures have applications in the calculus of variations and the study of nonlinear partial differential equations...
- Optimal controlOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
- Direct method in calculus of variationsDirect method in calculus of variationsIn the calculus of variations, a topic in mathematics, the direct method is a general method for constructing a proof of the existence of a minimizer for a given functional, introduced by Zaremba and David Hilbert around 1900. The method relies on methods of functional analysis and topology...
- Noether's theoremNoether's theoremNoether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
Reference books
- Gelfand, I.M.Israel GelfandIsrael Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
and Fomin, S.V.Sergei FominSergei Vasilyevich Fomin was a Soviet mathematician whowas co-author with Kolmogorov of Introductory real analysis,and co-author with I.M. Gelfand of Calculus of Variations ,both books that are widely read in Russian and in English....
: Calculus of Variations, Dover Publ., 2000. - Lebedev, L.P. and Cloud, M.J.: The Calculus of Variations and Functional Analysis with Optimal Control and Applications in Mechanics, World Scientific, 2003, pages 1–98.
- Charles Fox: An Introduction to the Calculus of Variations, Dover Publ., 1987.
- Forsyth, A.R.: Calculus of Variations, Dover, 1960.
- Sagan, Hans: Introduction to the Calculus of Variations, Dover, 1992.
- Weinstock, Robert: Calculus of Variations with Applications to Physics and Engineering, Dover, 1974.
- Clegg, J.C.: Calculus of Variations, Interscience Publishers Inc., 1968.
- Courant, R.Richard CourantRichard Courant was a German American mathematician.- Life :Courant was born in Lublinitz in the German Empire's Prussian Province of Silesia. During his youth, his parents had to move quite often, to Glatz, Breslau, and in 1905 to Berlin. He stayed in Breslau and entered the university there...
: Dirichlet's principle, conformal mapping and minimal surfaces. Interscience, 1950. - Courant, R. and D. HilbertDavid HilbertDavid Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
: Methods of Mathematical Physics, Vol I. Interscience Press, 1953. - Elsgolc, L.E.: Calculus of Variations, Pergamon Press Ltd., 1962.
- Jost, J. and X. Li-Jost: Calculus of Variations. Cambridge University Press, 1998.
- Bolza, O.Oskar BolzaOskar Bolza was a German mathematician, and student of Felix Klein. He was born in Bad Bergzabern, Rhenish Palatinate, and his parents were Luise Koenig and Moritz Bolza....
: Lectures on the Calculus of Variations. Chelsea Publishing Company, 1904, available on Digital Mathematics library http://quod.lib.umich.edu/cgi/t/text/text-idx?c=umhistmath;idno=ACM2513. 2nd edition republished in 1961, paperback in 2005, ISBN 978-1418182014.

