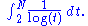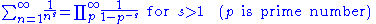Analytic number theory
Encyclopedia
In mathematics
, analytic number theory is a branch of number theory
that uses methods from mathematical analysis
to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions
. Another major milestone in the subject is the prime number theorem
.
Analytic number theory can be split up into two major parts, divided more by the type of problems they attempt to solve than fundamental differences in technique. Multiplicative number theory
deals with the distribution of the prime number
s, such as estimating the number of primes in an interval, and includes the prime number theorem and Dirichlet's theorem on primes in arithmetic progressions. Additive number theory
is concerned with the additive structure of the integers, such as Goldbach's conjecture
that every even number greater than 2 is the sum of two primes. One of the main results in additive number theory is the solution to Waring's problem
.
Developments within analytic number theory are often refinements of earlier techniques, which reduce the error terms and widen their applicability. For example, the circle method
of Hardy
and Littlewood
was conceived as applying to power series near the unit circle
in the complex plane
; it is now thought of in terms of finite exponential sums (that is, on the unit circle, but with the power series truncated). The needs of diophantine approximation
are for auxiliary functions that aren't generating function
s—their coefficients are constructed by use of a pigeonhole principle—and involve several complex variables
.
The fields of diophantine approximation and transcendence theory have expanded, to the point that the techniques have been applied to the Mordell conjecture.
The biggest technical change after 1950 has been the development of sieve methods
as a tool, particularly in multiplicative problems. These are combinatorial
in nature, and quite varied. The extremal branch of combinatorial theory has in return been greatly influenced by the value placed in analytic number theory on quantitative upper and lower bounds. Another recent development is probabilistic number theory
, which uses tools from probability theory to estimate the distribution of number theoretic functions, such as how many prime divisors a number has.
showed that there are an infinite number of primes but it is very difficult to find an efficient method for determining whether or not a number is prime, especially a large number. A related but easier problem is to determine the asymptotic distribution of the prime numbers; that is, a rough description of how many primes are smaller than a given number. Gauss, amongst others, after computing a large list of primes, conjectured that the number of primes less than or equal to a large number N is close to the value of the integral
In 1859 Bernhard Riemann
used complex analysis and a special meromorphic function now known as the Riemann zeta function to derive an analytic expression for the number of primes less than or equal to a real number x. Remarkably, the main term in Riemann's formula was exactly the above integral, lending substantial weight to Gauss's conjecture. Riemann found that the error terms in this expression, and hence the manner in which the primes are distributed, are closely related to the complex zeros of the zeta function. Using Riemann's ideas and by getting more information on the zeros of the zeta function, Jacques Hadamard
and Charles Jean de la Vallée-Poussin
managed to complete the proof of Gauss's conjecture. In particular, they proved that if
then
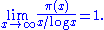
This remarkable result is what is now known as the Prime Number Theorem
. It is a central result in analytic number theory. Loosely speaking, it states that given a large number N, the number of primes less than or equal to N is about N/log(N).
More generally, the same question can be asked about the number of primes in any arithmetic progression
a+nq for any integer n. In one of the first applications of analytic techniques to number theory, Dirichlet proved that any arithmetic progression with a and q coprime contains infinitely many primes. The prime number theorem can be generalised to this problem; letting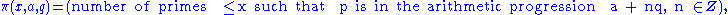
then if a and q are coprime,

There are also many deep and wide ranging conjectures in number theory whose proofs seem too difficult for current techniques, such as the Twin prime conjecture
which asks whether there are infinitely many primes p such that p + 2 is prime. On the assumption of the Elliott-Halberstam conjecture
it has been proven recently (by Daniel Goldston
, János Pintz
, Cem Yıldırım
) that there are infinitely many primes p such that p + k is prime for some positive even k less than 16.
, which asks whether it is possible, for any k ≥ 2, to write any positive integer as the sum of a bounded number of kth powers,
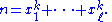
The case for squares, k = 2, was answered
by Lagrange in 1770, who proved that every positive integer is the sum of at most four squares. The general case was proved by Hilbert
in 1909, using algebraic techniques which gave no explicit bounds. An important breakthrough was the application of analytic tools to the problem by Hardy
and Littlewood
. These techniques are known as the circle method, and give explicit upper bounds for the function G(k), the smallest number of kth powers needed, such as Vinogradov
's bound
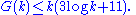
One of the most important examples is the Gauss circle problem
, which asks for integers points (x y) which satisfy
In geometrical terms, given a circle centered about the origin in the plane with radius r, the problem asks how many integer lattice points lie on or inside the circle. It is not hard to prove that the answer is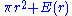 , where
, where 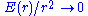 as
as 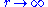 . Again, the difficult part and a great achievement of analytic number theory is obtaining specific upper bounds on the error term E(r).
. Again, the difficult part and a great achievement of analytic number theory is obtaining specific upper bounds on the error term E(r).
It was shown by Gauss that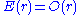 . In general, an O(r) error term would be possible with the unit circle (or, more properly, the closed unit disk) replaced by the dilates of any bounded planar region with piecewise smooth boundary. Furthermore, replacing the unit circle by the unit square, the error term for the general problem can be as large as a linear function of r. Therefore getting an error bound of the form
. In general, an O(r) error term would be possible with the unit circle (or, more properly, the closed unit disk) replaced by the dilates of any bounded planar region with piecewise smooth boundary. Furthermore, replacing the unit circle by the unit square, the error term for the general problem can be as large as a linear function of r. Therefore getting an error bound of the form 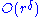
for some in the case of the circle is a significant improvement. The first to attain this was
in the case of the circle is a significant improvement. The first to attain this was
Sierpiński in 1906, who showed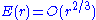 . In 1915, Hardy and Landau
. In 1915, Hardy and Landau
each showed that one does not have . Since then the goal has been to show that for each fixed
. Since then the goal has been to show that for each fixed  there exists a real number
there exists a real number 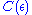 such that
such that 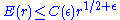 .
.
In 2000 Huxley
showed that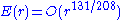 , which is the best published result.
, which is the best published result.
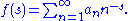
Depending on the choice of coefficients , this series may converge everywhere, nowhere, or on some half plane. In many cases, even where the series does not converge everywhere, the holomorphic function it defines may be analytically continued to a meromorphic function on the entire complex plane. The utility of functions like this in multiplicative problems can be seen in the formal identity
, this series may converge everywhere, nowhere, or on some half plane. In many cases, even where the series does not converge everywhere, the holomorphic function it defines may be analytically continued to a meromorphic function on the entire complex plane. The utility of functions like this in multiplicative problems can be seen in the formal identity

hence the coefficients of the product of two Dirichlet series are the multiplicative convolutions of the original coefficients. Furthermore, techniques such as partial summation and Tauberian theorems can be used to get information about the coefficients from analytic information about the Dirichlet series. Thus a common method for estimating a multiplicative function is to express it as a Dirichlet series (or a product of simpler Dirichlet series using convolution identities), examine this series as a complex function and then convert this analytic information back into information about the original function.
implies that
Euler's proof of the infinity of prime number
s makes use of the divergence of the term at the left hand side for s = 1 (the so-called harmonic series
), a purely analytic result. Euler was also the first to use analytical arguments for the purpose of studying properties of integers, specifically by constructing generating power series
. This was the beginning of analytic number theory.
Later, Riemann considered this function for complex values of s and showed that this function can be extended to a meromorphic function
on the entire plane with a simple pole at s = 1. This function is now known as the Riemann Zeta function and is denoted by ζ(s). There is a plethora of literature on this function and the function is a special case of the more general Dirichlet L-functions.
Analytic number theorists are often interested in the error of approximations such as the prime number theorem. In this case, the error is smaller than x/log x. Riemann's formula for π(x) shows that the error term in this approximation can be expressed in terms of the zeros of the zeta function. In his 1859 paper
, Riemann conjectured that all the "non-trivial" zeros of ζ lie on the line but never provided a proof of this statement. This famous and long-standing conjecture is known as the Riemann Hypothesis
but never provided a proof of this statement. This famous and long-standing conjecture is known as the Riemann Hypothesis
and has many deep implications in number theory; in fact, many important theorems have been proved under the assumption that the hypothesis is true. For example under the assumption of the Riemann Hypothesis, the error term in the prime number theorem is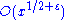 .
.
In the early 20th century G.H.Hardy and Littlewood
proved many results about the zeta function in an attempt to prove the Riemann Hypothesis. In fact, in 1914,
Hardy proved that there were infinitely many zeros of the zeta function on the critical line
This led to several theorems describing the density of the zeros on the critical line.
On specialized aspects the following books have become especially well-known:
Certain topics have not yet reached book form in any depth. Some examples are
(i) Montgomery's pair correlation conjecture
and the work that initiated from it,
(ii) the new results of Goldston, Pintz and Yilidrim on small gaps between primes
, and
(iii) the Green–Tao theorem showing that arbitrarily long arithmetic progressions of primes exist.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, analytic number theory is a branch of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
that uses methods from mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic progressions
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
. Another major milestone in the subject is the prime number theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
.
Analytic number theory can be split up into two major parts, divided more by the type of problems they attempt to solve than fundamental differences in technique. Multiplicative number theory
Multiplicative number theory
Multiplicative number theory is a subfield of analytic number theory that deals with prime numbers and with factorization and divisors. The focus is usually on developing approximate formulas for counting these objects in various contexts. The prime number theorem is a key result in this subject...
deals with the distribution of the prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, such as estimating the number of primes in an interval, and includes the prime number theorem and Dirichlet's theorem on primes in arithmetic progressions. Additive number theory
Additive number theory
In number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian groups and commutative semigroups with an operation of addition. Additive number theory has...
is concerned with the additive structure of the integers, such as Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
that every even number greater than 2 is the sum of two primes. One of the main results in additive number theory is the solution to Waring's problem
Waring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
.
Developments within analytic number theory are often refinements of earlier techniques, which reduce the error terms and widen their applicability. For example, the circle method
Hardy-Littlewood circle method
In mathematics, the Hardy–Littlewood circle method is one of the most frequently used techniques of analytic number theory. It is named for G. H. Hardy and J. E...
of Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Littlewood
John Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
was conceived as applying to power series near the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
; it is now thought of in terms of finite exponential sums (that is, on the unit circle, but with the power series truncated). The needs of diophantine approximation
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
are for auxiliary functions that aren't generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s—their coefficients are constructed by use of a pigeonhole principle—and involve several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
.
The fields of diophantine approximation and transcendence theory have expanded, to the point that the techniques have been applied to the Mordell conjecture.
The biggest technical change after 1950 has been the development of sieve methods
Sieve theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
as a tool, particularly in multiplicative problems. These are combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
in nature, and quite varied. The extremal branch of combinatorial theory has in return been greatly influenced by the value placed in analytic number theory on quantitative upper and lower bounds. Another recent development is probabilistic number theory
Probabilistic number theory
Probabilistic number theory is a subfield of number theory, which explicitly uses probability to answer questions of number theory. One basic idea underlying it is that different prime numbers are, in some serious sense, like independent random variables...
, which uses tools from probability theory to estimate the distribution of number theoretic functions, such as how many prime divisors a number has.
Problems and results in analytic number theory
The great theorems and results within analytic number theory tend not to be exact structural results about the integers, for which algebraic and geometrical tools are more appropriate. Instead, they give approximate bounds and estimates for various number theoretical functions, as the following examples illustrate.Multiplicative number theory
EuclidEuclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
showed that there are an infinite number of primes but it is very difficult to find an efficient method for determining whether or not a number is prime, especially a large number. A related but easier problem is to determine the asymptotic distribution of the prime numbers; that is, a rough description of how many primes are smaller than a given number. Gauss, amongst others, after computing a large list of primes, conjectured that the number of primes less than or equal to a large number N is close to the value of the integral
In 1859 Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
used complex analysis and a special meromorphic function now known as the Riemann zeta function to derive an analytic expression for the number of primes less than or equal to a real number x. Remarkably, the main term in Riemann's formula was exactly the above integral, lending substantial weight to Gauss's conjecture. Riemann found that the error terms in this expression, and hence the manner in which the primes are distributed, are closely related to the complex zeros of the zeta function. Using Riemann's ideas and by getting more information on the zeros of the zeta function, Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
and Charles Jean de la Vallée-Poussin
Charles Jean de la Vallée-Poussin
Charles-Jean Étienne Gustave Nicolas de la Vallée Poussin was a Belgian mathematician. He is most well known for proving the Prime number theorem.The king of Belgium ennobled him with the title of baron.-Biography:...
managed to complete the proof of Gauss's conjecture. In particular, they proved that if

then
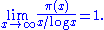
This remarkable result is what is now known as the Prime Number Theorem
Prime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. It is a central result in analytic number theory. Loosely speaking, it states that given a large number N, the number of primes less than or equal to N is about N/log(N).
More generally, the same question can be asked about the number of primes in any arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
a+nq for any integer n. In one of the first applications of analytic techniques to number theory, Dirichlet proved that any arithmetic progression with a and q coprime contains infinitely many primes. The prime number theorem can be generalised to this problem; letting
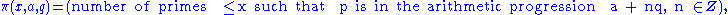
then if a and q are coprime,

There are also many deep and wide ranging conjectures in number theory whose proofs seem too difficult for current techniques, such as the Twin prime conjecture
Twin prime
A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
which asks whether there are infinitely many primes p such that p + 2 is prime. On the assumption of the Elliott-Halberstam conjecture
Elliott-Halberstam conjecture
In number theory, the Elliott–Halberstam conjecture is a conjecture about the distribution of prime numbers in arithmetic progressions. It has many applications in sieve theory. It is named for Peter D. T. A. Elliott and Heini Halberstam....
it has been proven recently (by Daniel Goldston
Daniel Goldston
Daniel Alan Goldston is an American mathematician who specializes in number theory. He is currently a professor of mathematics at San Jose State University....
, János Pintz
János Pintz
János Pintz is a Hungarian mathematician working in analytic number theory. He is a fellow of the Rényi Mathematical Institute and is also a member of the Hungarian Academy of Sciences.-Mathematical results:...
, Cem Yıldırım
Cem Yildirim
Cem Yalçın Yıldırım is a Turkish mathematician who specializes in number theory. He obtained his PhD from the University of Toronto in 1990. His advisor was John Friedlander...
) that there are infinitely many primes p such that p + k is prime for some positive even k less than 16.
Additive number theory
One of the most important problems in additive number theory is Waring's problemWaring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
, which asks whether it is possible, for any k ≥ 2, to write any positive integer as the sum of a bounded number of kth powers,
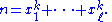
The case for squares, k = 2, was answered
Lagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
by Lagrange in 1770, who proved that every positive integer is the sum of at most four squares. The general case was proved by Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
in 1909, using algebraic techniques which gave no explicit bounds. An important breakthrough was the application of analytic tools to the problem by Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and Littlewood
John Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
. These techniques are known as the circle method, and give explicit upper bounds for the function G(k), the smallest number of kth powers needed, such as Vinogradov
Ivan Matveyevich Vinogradov
Ivan Matveevich Vinogradov was a Soviet mathematician, who was one of the creators of modern analytic number theory, and also a dominant figure in mathematics in the USSR. He was born in the Velikiye Luki district, Pskov Oblast. He graduated from the University of St...
's bound
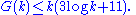
Diophantine problems
Diophantine problems are concerned with integer solutions to polynomial equations, and especially how many you can expect to find within a given range.One of the most important examples is the Gauss circle problem
Gauss circle problem
In mathematics, the Gauss circle problem is the problem of determining how many integer lattice points there are in a circle centred at the origin and with radius r. The first progress on a solution was made by Carl Friedrich Gauss, hence its name....
, which asks for integers points (x y) which satisfy

In geometrical terms, given a circle centered about the origin in the plane with radius r, the problem asks how many integer lattice points lie on or inside the circle. It is not hard to prove that the answer is
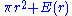 , where
, where 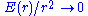 as
as 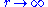 . Again, the difficult part and a great achievement of analytic number theory is obtaining specific upper bounds on the error term E(r).
. Again, the difficult part and a great achievement of analytic number theory is obtaining specific upper bounds on the error term E(r).It was shown by Gauss that
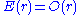 . In general, an O(r) error term would be possible with the unit circle (or, more properly, the closed unit disk) replaced by the dilates of any bounded planar region with piecewise smooth boundary. Furthermore, replacing the unit circle by the unit square, the error term for the general problem can be as large as a linear function of r. Therefore getting an error bound of the form
. In general, an O(r) error term would be possible with the unit circle (or, more properly, the closed unit disk) replaced by the dilates of any bounded planar region with piecewise smooth boundary. Furthermore, replacing the unit circle by the unit square, the error term for the general problem can be as large as a linear function of r. Therefore getting an error bound of the form 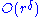
for some
 in the case of the circle is a significant improvement. The first to attain this was
in the case of the circle is a significant improvement. The first to attain this wasSierpiński in 1906, who showed
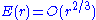 . In 1915, Hardy and Landau
. In 1915, Hardy and LandauEdmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
each showed that one does not have
 . Since then the goal has been to show that for each fixed
. Since then the goal has been to show that for each fixed  there exists a real number
there exists a real number 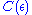 such that
such that 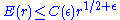 .
.In 2000 Huxley
Martin Huxley
Martin Neil Huxley is a British mathematician, working in the field of analytic number theory.He was awarded a PhD from the University of Cambridge in 1970, the year after his supervisor Harold Davenport had died...
showed that
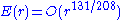 , which is the best published result.
, which is the best published result.Dirichlet series
One of the most useful tools in multiplicative number theory are Dirichlet series, which are functions of a complex variable defined by an infinite series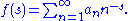
Depending on the choice of coefficients
 , this series may converge everywhere, nowhere, or on some half plane. In many cases, even where the series does not converge everywhere, the holomorphic function it defines may be analytically continued to a meromorphic function on the entire complex plane. The utility of functions like this in multiplicative problems can be seen in the formal identity
, this series may converge everywhere, nowhere, or on some half plane. In many cases, even where the series does not converge everywhere, the holomorphic function it defines may be analytically continued to a meromorphic function on the entire complex plane. The utility of functions like this in multiplicative problems can be seen in the formal identity
hence the coefficients of the product of two Dirichlet series are the multiplicative convolutions of the original coefficients. Furthermore, techniques such as partial summation and Tauberian theorems can be used to get information about the coefficients from analytic information about the Dirichlet series. Thus a common method for estimating a multiplicative function is to express it as a Dirichlet series (or a product of simpler Dirichlet series using convolution identities), examine this series as a complex function and then convert this analytic information back into information about the original function.
The Riemann zeta function
Euler showed that the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
implies that
Euler's proof of the infinity of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s makes use of the divergence of the term at the left hand side for s = 1 (the so-called harmonic series
Harmonic series
Harmonic series may refer to either of two related concepts:*Harmonic series *Harmonic series...
), a purely analytic result. Euler was also the first to use analytical arguments for the purpose of studying properties of integers, specifically by constructing generating power series
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
. This was the beginning of analytic number theory.
Later, Riemann considered this function for complex values of s and showed that this function can be extended to a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
on the entire plane with a simple pole at s = 1. This function is now known as the Riemann Zeta function and is denoted by ζ(s). There is a plethora of literature on this function and the function is a special case of the more general Dirichlet L-functions.
Analytic number theorists are often interested in the error of approximations such as the prime number theorem. In this case, the error is smaller than x/log x. Riemann's formula for π(x) shows that the error term in this approximation can be expressed in terms of the zeros of the zeta function. In his 1859 paper
On the Number of Primes Less Than a Given Magnitude
die Anzahl der Primzahlen unter einer gegebenen is a seminal 8-page paper by Bernhard Riemann published in the November 1859 edition of the Monatsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin.Although it is the only paper he ever published on number theory, it...
, Riemann conjectured that all the "non-trivial" zeros of ζ lie on the line
 but never provided a proof of this statement. This famous and long-standing conjecture is known as the Riemann Hypothesis
but never provided a proof of this statement. This famous and long-standing conjecture is known as the Riemann HypothesisRiemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
and has many deep implications in number theory; in fact, many important theorems have been proved under the assumption that the hypothesis is true. For example under the assumption of the Riemann Hypothesis, the error term in the prime number theorem is
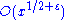 .
.In the early 20th century G.H.Hardy and Littlewood
Littlewood
Littlewood is a surname, and may refer to* Barclay Littlewood, British entrepreneur* Dominic Littlewood, British television presenter and entrepreneur* Dudley E...
proved many results about the zeta function in an attempt to prove the Riemann Hypothesis. In fact, in 1914,
Hardy proved that there were infinitely many zeros of the zeta function on the critical line

This led to several theorems describing the density of the zeros on the critical line.
Further reading
- Ayoub, Introduction to the Analytic Theory of Numbers
- H. L. Montgomery and R. C. Vaughan, Multiplicative Number Theory I : Classical Theory
- H. Iwaniec and E. Kowalski, Analytic Number Theory.
- D. J. Newman, Analytic number theory, Springer, 1998
On specialized aspects the following books have become especially well-known:
- H. Halberstam and H. E. Richert, Sieve Methods
- R. C. Vaughan, The Hardy-Littlewood method, 2nd. edn.
Certain topics have not yet reached book form in any depth. Some examples are
(i) Montgomery's pair correlation conjecture
Montgomery's pair correlation conjecture
In mathematics, Montgomery's pair correlation conjecture is a conjecture made by that the pair correlation between pairs of zeros of the Riemann zeta function is1-\left^2 +\delta,...
and the work that initiated from it,
(ii) the new results of Goldston, Pintz and Yilidrim on small gaps between primes
Twin prime
A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
, and
(iii) the Green–Tao theorem showing that arbitrarily long arithmetic progressions of primes exist.