Proof of the Euler product formula for the Riemann zeta function
Encyclopedia
Leonhard Euler
proved the Euler product formula for the Riemann zeta function in his thesis Variae observationes circa series infinitas' '(Various Observations about Infinite Series), published by St Petersburg Academy in 1737.
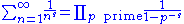
where the left hand side equals the Riemann zeta function:
and the product on the right hand side extends over all prime number
s p:
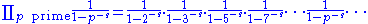
only makes use of simple algebra that most high school students can understand. This was originally the method by which Euler discovered the formula. There is a certain sieving
property that we can use to our advantage:
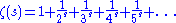
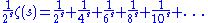
Subtracting the second from the first we remove all elements that have a factor of 2:
Repeating for the next term:
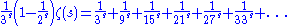
Subtracting again we get:
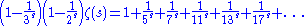
where all elements having a factor of 3 or 2 (or both) are removed.
It can be seen that the right side is being sieved. Repeating infinitely we get:
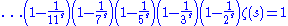
Dividing both sides by everything but the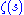
we obtain:
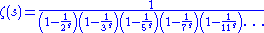
This can be written more concisely as an infinite product over all primes p:
To make this proof rigorous, we need only observe that when Re(s) > 1, the sieved right-hand side approaches 1, which follows immediately from the convergence of the Dirichlet series for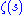
.
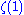
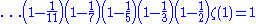
which can also be written as,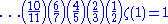
which is,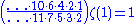
as,
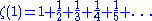
thus,
We know that the left-hand side of the equation diverges to infinity therefore the numerator on the right-hand side (the primorial
) must also be infinite for divergence. This proves that there are infinitely many prime numbers.
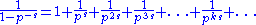
When
, we have 
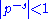and this series converges absolutely
. Hence we may take a finite number of factors, multiply them together, and rearrange terms. Taking all the primes p up to some prime number limit q, we have
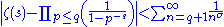
where σ is the real part of s. By the fundamental theorem of arithmetic
, the partial product when expanded out gives a sum consisting of those terms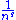
where n is a product of primes less than or equal to q. The inequality results from the fact that therefore only integers larger than q can fail to appear in this expanded out partial product. Since the difference between the partial product and ζ(s) goes to zero when σ > 1, we have convergence in this region.
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
proved the Euler product formula for the Riemann zeta function in his thesis Variae observationes circa series infinitas' '(Various Observations about Infinite Series), published by St Petersburg Academy in 1737.
The Euler product formula
The Euler product formula for the Riemann zeta function reads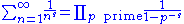where the left hand side equals the Riemann zeta function:
and the product on the right hand side extends over all prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s p:
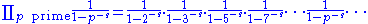
Proof of the Euler product formula
This sketch of a proofMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
only makes use of simple algebra that most high school students can understand. This was originally the method by which Euler discovered the formula. There is a certain sieving
Sieve of Eratosthenes
In mathematics, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to a specified integer....
property that we can use to our advantage:
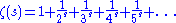
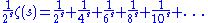
Subtracting the second from the first we remove all elements that have a factor of 2:
Repeating for the next term:
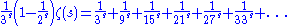
Subtracting again we get:
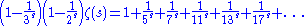
where all elements having a factor of 3 or 2 (or both) are removed.
It can be seen that the right side is being sieved. Repeating infinitely we get:
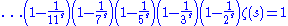
Dividing both sides by everything but the
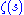we obtain: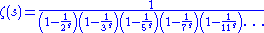This can be written more concisely as an infinite product over all primes p:
To make this proof rigorous, we need only observe that when Re(s) > 1, the sieved right-hand side approaches 1, which follows immediately from the convergence of the Dirichlet series for
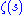.The case s=1
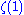
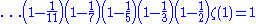
An interesting result can be found forwhich can also be written as,
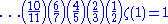
which is,
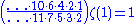
as,
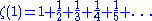
thus,
We know that the left-hand side of the equation diverges to infinity therefore the numerator on the right-hand side (the primorial
Primorial
In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...
) must also be infinite for divergence. This proves that there are infinitely many prime numbers.
Another proof
Each factor (for a given prime p) in the product above can be expanded to a geometric series consisting of the reciprocal of p raised to multiples of s, as follows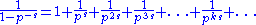When
, we have 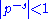and this series converges absolutelySeries (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. Hence we may take a finite number of factors, multiply them together, and rearrange terms. Taking all the primes p up to some prime number limit q, we have
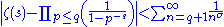
where σ is the real part of s. By the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
, the partial product when expanded out gives a sum consisting of those terms
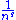where n is a product of primes less than or equal to q. The inequality results from the fact that therefore only integers larger than q can fail to appear in this expanded out partial product. Since the difference between the partial product and ζ(s) goes to zero when σ > 1, we have convergence in this region.