
History of mathematics
Encyclopedia
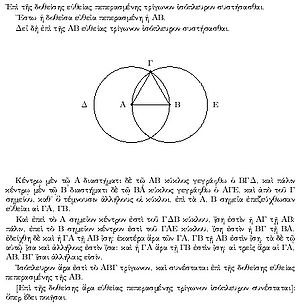
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and, to a lesser extent, an investigation into the mathematical methods and notation of the past.
Before the modern age
Modern Age
Modern Age is an American conservative academic quarterly journal, founded in 1957 by Russell Kirk in close collaboration with Henry Regnery...
and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. The most ancient mathematical texts available are Plimpton 322
Plimpton 322
Plimpton 322 is a Babylonian clay tablet, notable as containing an example of Babylonian mathematics. It has number 322 in the G.A. Plimpton Collection at Columbia University...
(Babylonian mathematics
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
c. 1900 BC), the Rhind Mathematical Papyrus
Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus , is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased the papyrus in 1858 in Luxor, Egypt; it was apparently found during illegal excavations in or near the Ramesseum. It dates to around 1650 BC...
(Egyptian mathematics c. 2000-1800 BC) and the Moscow Mathematical Papyrus
Moscow Mathematical Papyrus
The Moscow Mathematical Papyrus is an ancient Egyptian mathematical papyrus, also called the Golenishchev Mathematical Papyrus, after its first owner, Egyptologist Vladimir Golenishchev. Golenishchev bought the papyrus in 1892 or 1893 in Thebes...
(Egyptian mathematics
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
c. 1890 BC). All of these texts concern the so-called Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, which seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.
The study of mathematics as a subject in its own right begins in the 6th century BC with the Pythagoreans, who coined the term "mathematics" from the ancient Greek μάθημα (mathema), meaning "subject of instruction". Greek mathematics
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor in proofs
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
) and expanded the subject matter of mathematics. Chinese mathematics
Counting rods
Counting rods are small bars, typically 3–14 cm long, used by mathematicians for calculation in China, Japan, Korea, and Vietnam. They are placed either horizontally or vertically to represent any number and any fraction....
made early contributions, including a place value system. The Hindu-Arabic numeral system
Hindu-Arabic numeral system
The Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
and the rules for the use of its operations, in use throughout the world today, likely evolved over the course of the first millennium AD in India
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
and was transmitted to the west via Islamic mathematics. Islamic mathematics
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
, in turn, developed and expanded the mathematics known to these civilizations. Many Greek and Arabic texts on mathematics were then translated into Latin, which led to further development of mathematics in medieval Europe
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
.
From ancient times through the Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
, bursts of mathematical creativity were often followed by centuries of stagnation. Beginning in Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
in the 16th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
that continues through the present day.
Prehistoric mathematics
The origins of mathematical thought lie in the concepts of numberNumber
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
, magnitude
Magnitude
Magnitude Is A Part Of An EarthquakesMagnitude may refer to:In mathematics:*Magnitude , the relative size of a mathematical object*Magnitude , a term for the size or length of a vector...
, and form
FORM
FORM is the bimonthly membership magazine of the American Institute of Architects Los Angeles , and is published in Glendale, California by Balcony Media, Inc. The magazine was launched in 2007, and covers modern design and architecture...
. Modern studies of animal cognition have shown that these concepts are not unique to humans. Such concepts would have been part of everyday life in hunter-gatherer societies. The idea of the "number" concept evolving gradually over time is supported by the existence of languages which preserve the distinction between "one", "two", and "many", but not of numbers larger than two.
The oldest known possibly mathematical object is the Lebombo bone, discovered in the Lebombo mountains of Swaziland
Swaziland
Swaziland, officially the Kingdom of Swaziland , and sometimes called Ngwane or Swatini, is a landlocked country in Southern Africa, bordered to the north, south and west by South Africa, and to the east by Mozambique...
and dated to approximately 35,000 BC. It consists of 29 distinct notches cut into a baboon's fibula. Also prehistoric
Prehistory
Prehistory is the span of time before recorded history. Prehistory can refer to the period of human existence before the availability of those written records with which recorded history begins. More broadly, it refers to all the time preceding human existence and the invention of writing...
artifact
Artifact (archaeology)
An artifact or artefact is "something made or given shape by man, such as a tool or a work of art, esp an object of archaeological interest"...
s discovered in Africa and France
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
, dated between 35,000 and 20,000
Upper Paleolithic
The Upper Paleolithic is the third and last subdivision of the Paleolithic or Old Stone Age as it is understood in Europe, Africa and Asia. Very broadly it dates to between 40,000 and 10,000 years ago, roughly coinciding with the appearance of behavioral modernity and before the advent of...
years old, suggest early attempts to quantify
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
time.
The Ishango bone
Ishango bone
The Ishango bone is a bone tool, dated to the Upper Paleolithic era. It is a dark brown length of bone, the fibula of a baboon, with a sharp piece of quartz affixed to one end, perhaps for engraving...
, found near the headwaters of the Nile
Nile
The Nile is a major north-flowing river in North Africa, generally regarded as the longest river in the world. It is long. It runs through the ten countries of Sudan, South Sudan, Burundi, Rwanda, Democratic Republic of the Congo, Tanzania, Kenya, Ethiopia, Uganda and Egypt.The Nile has two major...
river (northeastern Congo
Democratic Republic of the Congo
The Democratic Republic of the Congo is a state located in Central Africa. It is the second largest country in Africa by area and the eleventh largest in the world...
), may be as much as 20,000
Upper Paleolithic
The Upper Paleolithic is the third and last subdivision of the Paleolithic or Old Stone Age as it is understood in Europe, Africa and Asia. Very broadly it dates to between 40,000 and 10,000 years ago, roughly coinciding with the appearance of behavioral modernity and before the advent of...
years old and consists of a series of tally marks carved in three columns running the length of the bone. Common interpretations are that the Ishango bone shows either the earliest known demonstration of sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
s of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s or a six month lunar calendar. In the book How Mathematics Happened: The First 50,000 Years, Peter Rudman argues that the development of the concept of prime numbers could only have come about after the concept of division, which he dates to after 10,000 BC, with prime numbers probably not being understood until about 500 BC. He also writes that "no attempt has been made to explain why a tally of something should exhibit multiples of two, prime numbers between 10 and 20, and some numbers that are almost multiples of 10."
Predynastic Egypt
Predynastic Egypt
The Prehistory of Egypt spans the period of earliest human settlement to the beginning of the Early Dynastic Period of Egypt in ca. 3100 BC, starting with King Menes/Narmer....
ians of the 5th millennium BC pictorially represented geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
designs. It has been claimed that megalith
Megalith
A megalith is a large stone that has been used to construct a structure or monument, either alone or together with other stones. Megalithic describes structures made of such large stones, utilizing an interlocking system without the use of mortar or cement.The word 'megalith' comes from the Ancient...
ic monuments in England
England
England is a country that is part of the United Kingdom. It shares land borders with Scotland to the north and Wales to the west; the Irish Sea is to the north west, the Celtic Sea to the south west, with the North Sea to the east and the English Channel to the south separating it from continental...
and Scotland
Scotland
Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
, dating from the 3rd millennium BC, incorporate geometric ideas such as circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s, ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s, and Pythagorean triple
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s in their design.
Mesopotamian mathematics

Babylonia
Babylonia was an ancient cultural region in central-southern Mesopotamia , with Babylon as its capital. Babylonia emerged as a major power when Hammurabi Babylonia was an ancient cultural region in central-southern Mesopotamia (present-day Iraq), with Babylon as its capital. Babylonia emerged as...
n mathematics refers to any mathematics of the people of Mesopotamia
Mesopotamia
Mesopotamia is a toponym for the area of the Tigris–Euphrates river system, largely corresponding to modern-day Iraq, northeastern Syria, southeastern Turkey and southwestern Iran.Widely considered to be the cradle of civilization, Bronze Age Mesopotamia included Sumer and the...
(modern Iraq
Iraq
Iraq ; officially the Republic of Iraq is a country in Western Asia spanning most of the northwestern end of the Zagros mountain range, the eastern part of the Syrian Desert and the northern part of the Arabian Desert....
) from the days of the early Sumer
Sumer
Sumer was a civilization and historical region in southern Mesopotamia, modern Iraq during the Chalcolithic and Early Bronze Age....
ians through the Hellenistic period
Hellenistic period
The Hellenistic period or Hellenistic era describes the time which followed the conquests of Alexander the Great. It was so named by the historian J. G. Droysen. During this time, Greek cultural influence and power was at its zenith in Europe and Asia...
almost to the dawn of Christianity
Christianity
Christianity is a monotheistic religion based on the life and teachings of Jesus as presented in canonical gospels and other New Testament writings...
. It is named Babylonian mathematics due to the central role of Babylon
Babylon
Babylon was an Akkadian city-state of ancient Mesopotamia, the remains of which are found in present-day Al Hillah, Babil Province, Iraq, about 85 kilometers south of Baghdad...
as a place of study. Later under the Arab Empire
Caliphate
The term caliphate, "dominion of a caliph " , refers to the first system of government established in Islam and represented the political unity of the Muslim Ummah...
, Mesopotamia, especially Baghdad
Baghdad
Baghdad is the capital of Iraq, as well as the coterminous Baghdad Governorate. The population of Baghdad in 2011 is approximately 7,216,040...
, once again became an important center of study for Islamic mathematics
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
.
In contrast to the sparsity of sources in Egyptian mathematics
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
, our knowledge of Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s. Written in Cuneiform script
Cuneiform script
Cuneiform script )) is one of the earliest known forms of written expression. Emerging in Sumer around the 30th century BC, with predecessors reaching into the late 4th millennium , cuneiform writing began as a system of pictographs...
, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework.
The earliest evidence of written mathematics dates back to the ancient Sumer
Sumer
Sumer was a civilization and historical region in southern Mesopotamia, modern Iraq during the Chalcolithic and Early Bronze Age....
ians, who built the earliest civilization in Mesopotamia. They developed a complex system of metrology
Metrology
Metrology is the science of measurement. Metrology includes all theoretical and practical aspects of measurement. The word comes from Greek μέτρον , "measure" + "λόγος" , amongst others meaning "speech, oration, discourse, quote, study, calculation, reason"...
from 3000 BC. From around 2500 BC onwards, the Sumerians wrote multiplication table
Multiplication table
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
s on clay tablets and dealt with geometrical
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
exercises and division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
problems. The earliest traces of the Babylonian numerals also date back to this period.
The majority of recovered clay tablets date from 1800 to 1600 BC, and cover topics which include fractions, algebra, quadratic and cubic equations, and the calculation of regular
Regular number
Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
pairs
Twin prime
A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
. The tablets also include multiplication tables and methods for solving linear
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
and quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
s. The Babylonian tablet YBC 7289 gives an approximation of √2 accurate to five decimal places.
Babylonian mathematics were written using a sexagesimal (base-60) numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
. From this derives the modern day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 x 6) degrees in a circle, as well as the use of seconds and minutes of arc to denote fractions of a degree. Babylonian advances in mathematics were facilitated by the fact that 60 has many divisors. Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a true place-value system, where digits written in the left column represented larger values, much as in the decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
system. They lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context.
Egyptian mathematics
EgyptEgypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
ian mathematics refers to mathematics written in the Egyptian language
Egyptian language
Egyptian is the oldest known indigenous language of Egypt and a branch of the Afroasiatic language family. Written records of the Egyptian language have been dated from about 3400 BC, making it one of the oldest recorded languages known. Egyptian was spoken until the late 17th century AD in the...
. From the Hellenistic period
Hellenistic period
The Hellenistic period or Hellenistic era describes the time which followed the conquests of Alexander the Great. It was so named by the historian J. G. Droysen. During this time, Greek cultural influence and power was at its zenith in Europe and Asia...
, Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
replaced Egyptian as the written language of Egyptian
Egyptians
Egyptians are nation an ethnic group made up of Mediterranean North Africans, the indigenous people of Egypt.Egyptian identity is closely tied to geography. The population of Egypt is concentrated in the lower Nile Valley, the small strip of cultivable land stretching from the First Cataract to...
scholars. Mathematical study in Egypt
Egypt
Egypt , officially the Arab Republic of Egypt, Arabic: , is a country mainly in North Africa, with the Sinai Peninsula forming a land bridge in Southwest Asia. Egypt is thus a transcontinental country, and a major power in Africa, the Mediterranean Basin, the Middle East and the Muslim world...
later continued under the Arab Empire
Caliphate
The term caliphate, "dominion of a caliph " , refers to the first system of government established in Islam and represented the political unity of the Muslim Ummah...
as part of Islamic mathematics
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
, when Arabic became the written language of Egyptian scholars.
The most extensive Egyptian mathematical text is the Rhind papyrus (sometimes also called the Ahmes Papyrus after its author), dated to c. 1650 BC but likely a copy of an older document from the Middle Kingdom
Middle Kingdom of Egypt
The Middle Kingdom of Egypt is the period in the history of ancient Egypt stretching from the establishment of the Eleventh Dynasty to the end of the Fourteenth Dynasty, between 2055 BC and 1650 BC, although some writers include the Thirteenth and Fourteenth dynasties in the Second Intermediate...
of about 2000-1800 BC. It is an instruction manual for students in arithmetic and geometry. In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge, including composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
and prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s; arithmetic
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
, geometric
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
and harmonic mean
Harmonic mean
In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....
s; and simplistic understandings of both the Sieve of Eratosthenes
Sieve of Eratosthenes
In mathematics, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to a specified integer....
and perfect number theory
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
(namely, that of the number 6). It also shows how to solve first order linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
s as well as arithmetic and geometric series.
Another significant Egyptian mathematical text is the Moscow papyrus, also from the Middle Kingdom
Middle Kingdom of Egypt
The Middle Kingdom of Egypt is the period in the history of ancient Egypt stretching from the establishment of the Eleventh Dynasty to the end of the Fourteenth Dynasty, between 2055 BC and 1650 BC, although some writers include the Thirteenth and Fourteenth dynasties in the Second Intermediate...
period, dated to c. 1890 BC. It consists of what are today called word problems or story problems, which were apparently intended as entertainment. One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum
Frustum
In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it....
: "If you are told: A truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top. You are to square this 4, result 16. You are to double 4, result 8. You are to square 2, result 4. You are to add the 16, the 8, and the 4, result 28. You are to take one third of 6, result 2. You are to take 28 twice, result 56. See, it is 56. You will find it right."
Finally, the Berlin papyrus
Berlin papyrus
The Berlin Papyrus 6619, commonly known as the Berlin Papyrus, is an ancient Egyptian papyrus document from the Middle Kingdom. This papyrus was found at the ancient burial ground of Saqqara in the early 19th century CE....
(c. 1300 BC) shows that ancient Egyptians could solve a second-order algebraic equation.
Greek Mathematics
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
from the time of Thales of Miletus (~600 BC) to the closure of the Academy of Athens
Platonic Academy
The Academy was founded by Plato in ca. 387 BC in Athens. Aristotle studied there for twenty years before founding his own school, the Lyceum. The Academy persisted throughout the Hellenistic period as a skeptical school, until coming to an end after the death of Philo of Larissa in 83 BC...
in 529 AD. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to North Africa, but were united by culture and language. Greek mathematics of the period following Alexander the Great is sometimes called Hellenistic mathematics.
Greek mathematics was much more sophisticated than the mathematics that had been developed by earlier cultures. All surviving records of pre-Greek mathematics show the use of inductive reasoning, that is, repeated observations used to establish rules of thumb. Greek mathematicians, by contrast, used deductive reasoning. The Greeks used logic to derive conclusions from definitions and axioms, and used mathematical rigor to prove
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
them.
Greek mathematics is thought to have begun with Thales of Miletus (c. 624–c.546 BC) and Pythagoras of Samos (c. 582–c. 507 BC). Although the extent of the influence is disputed, they were probably inspired by Egyptian
Egyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
and Babylonian mathematics
Babylonian mathematics
Babylonian mathematics refers to any mathematics of the people of Mesopotamia, from the days of the early Sumerians to the fall of Babylon in 539 BC. Babylonian mathematical texts are plentiful and well edited...
. According to legend, Pythagoras traveled to Egypt to learn mathematics, geometry, and astronomy from Egyptian priests.

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
to solve problems such as calculating the height of pyramids and the distance of ships from the shore. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem
Thales' theorem
In geometry, Thales' theorem states that if A, B and C are points on a circle where the line AC is a diameter of the circle, then the angle ABC is a right angle. Thales' theorem is a special case of the inscribed angle theorem...
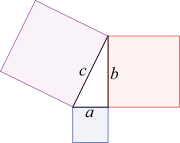
. As a result, he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. Pythagoras established the Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The Pythagoreans are credited with the first proof of the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, though the statement of the theorem has a long history, and with the proof of the existence of irrational numbers.

Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
(428/427 BC – 348/347 BC) is important in the history of mathematics for inspiring and guiding others. His Platonic Academy
Platonic Academy
The Academy was founded by Plato in ca. 387 BC in Athens. Aristotle studied there for twenty years before founding his own school, the Lyceum. The Academy persisted throughout the Hellenistic period as a skeptical school, until coming to an end after the death of Philo of Larissa in 83 BC...
, in Athens
Athens
Athens , is the capital and largest city of Greece. Athens dominates the Attica region and is one of the world's oldest cities, as its recorded history spans around 3,400 years. Classical Athens was a powerful city-state...
, became the mathematical center of the world in the 4th century BC, and it was from this school that the leading mathematicians of the day, such as Eudoxus of Cnidus
Eudoxus of Cnidus
Eudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
, came from. Plato also discussed the foundations of mathematics, clarified some of the definitions (e.g. that of a line as "breadthless length"), and reorganized the assumptions. The analytic method
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
is ascribed to Plato, while a formula for obtaining Pythagorean triples bears his name.
Eudoxus
Eudoxus of Cnidus
Eudoxus of Cnidus was a Greek astronomer, mathematician, scholar and student of Plato. Since all his own works are lost, our knowledge of him is obtained from secondary sources, such as Aratus's poem on astronomy...
(408–c.355 BC) developed the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
, a precursor of modern integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
and a theory of ratios that avoided the problem of incommensurable magnitudes. The former allowed the calculations of areas and volumes of curvilinear figures, while the latter enabled subsequent geometers to make significant advances in geometry. Though he made no specific technical mathematical discoveries, Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
(384—c.322 BC) contributed significantly to the development of mathematics by laying the foundations of logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
.
In the 3rd century BC, the premier center of mathematical education and research was the Musaeum
Musaeum
The Musaeum or Mouseion at Alexandria , which included the famous Library of Alexandria, was an institution founded, according to Johannes Tzetzes, by Ptolemy I Soter or, perhaps more likely, by Ptolemy II Philadelphus at Hellenistic Alexandria in Egypt. The Mouseion remained supported by the...
of Alexandria
Alexandria
Alexandria is the second-largest city of Egypt, with a population of 4.1 million, extending about along the coast of the Mediterranean Sea in the north central part of the country; it is also the largest city lying directly on the Mediterranean coast. It is Egypt's largest seaport, serving...
. It was there that Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
(c. 300 BC) taught, and wrote the Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, widely considered the most successful and influential textbook of all time. The Elements introduced mathematical rigor through the axiomatic method and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof. Although most of the contents of the Elements were already known, Euclid arranged them into a single, coherent logical framework. The Elements was known to all educated people in the West until the middle of the 20th century and its contents are still taught in geometry classes today. In addition to the familiar theorems of Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, the Elements was meant as an introductory textbook to all mathematical subjects of the time, such as number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and solid geometry
Solid geometry
In mathematics, solid geometry was the traditional name for the geometry of three-dimensional Euclidean space — for practical purposes the kind of space we live in. It was developed following the development of plane geometry...
, including proofs that the square root of two is irrational and that there are infinitely many prime numbers. Euclid also wrote extensively on other subjects, such as conic sections, optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
, and mechanics, but only half of his writings survive.
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
(c.287–212 BC) of Syracuse
Syracuse, Italy
Syracuse is a historic city in Sicily, the capital of the province of Syracuse. The city is notable for its rich Greek history, culture, amphitheatres, architecture, and as the birthplace of the preeminent mathematician and engineer Archimedes. This 2,700-year-old city played a key role in...
, widely considered the greatest mathematician of antiquity, used the method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
to calculate the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
under the arc of a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
with the summation of an infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
, in a manner not too dissimilar from modern calculus. He also showed one could use the method of exhaustion to calculate the value of π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
with as much precision as desired, and obtained the most accurate value of π then known, 3 < π < 3. He also studied the spiral bearing his name, obtained formulas for the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
s of surfaces of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
(paraboloid, ellipsoid, hyperboloid), and an ingenious system for expressing very large numbers. While he is also known for his contributions to physics and several advanced mechanical devices, Archimedes himself placed far greater value on the products of his thought and general mathematical principles. He regarded as his greatest achievement his finding of the surface area and volume of a sphere, which he obtained by proving these are 2/3 the surface area and volume a cylinder circumscribing the sphere.
Apollonius
Apollonius of Perga
Apollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
of Perga
Perga
Perga was an ancient Greek city in Anatolia and the capital of Pamphylia, now in Antalya province on the southwestern Mediterranean coast of Turkey. Today it is a large site of ancient ruins east of Antalya on the coastal plain. Located there is an acropolis dating back to the Bronze Age...
(c. 262-190 BC) made significant advances to the study of conic sections, showing that one can obtain all three varieties of conic section by varying the angle of the plane that cuts a double-napped cone. He also coined the terminology in use today for conic sections, namely parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
("place beside" or "comparison"), "ellipse" ("deficiency"), and "hyperbola" ("a throw beyond"). His work Conics is one of the best known and preserved mathematical works from antiquity, and in it he derives many theorems concerning conic sections that would prove invaluable to later mathematicians and astronomers studying planetary motion, such as Isaac Newton. While neither Apollonius nor any other Greek mathematicians made the leap to coordinate geometry, Apollonius' treatment of curves is in some ways similar to the modern treatment, and some of his work seems to anticipate the development of analytical geometry by Descartes some 1800 years later.
Around the same time, Eratosthenes of Cyrene of Cyrene
Cyrene
Cyrene may refer to:* Cyrene , a Greek mythological figure* Cyrene, Libya, an ancient Greek colony in North Africa* USS Cyrene , a motor torpedo boat tender* 133 Cyrene, an asteroid...
(c. 276-194 BC) devised the Sieve of Eratosthenes
Sieve of Eratosthenes
In mathematics, the sieve of Eratosthenes , one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to a specified integer....
for finding prime numbers. The 3rd century BC is generally regarded as the "Golden Age" of Greek mathematics, with advances in pure mathematics henceforth in relative decline. Nevertheless, in the centuries that followed significant advances were made in applied mathematics, most notably trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, largely to address the needs of astronomers. Hipparchus of Nicaea
Nicaea
Nicaea or Nikaia may be:*The ancient name of several places, including:** İznik, Turkey - formerly Nicaea capital of the Empire of Nicaea**Nice, France**Nicaea, Locris, a fortress city of the Locri Epicnemidii...
(c. 190-120 BC) is considered the founder of trigonometry for compiling the first known trigonometric table, and to him is also due the systematic use of the 360 degree circle. Heron of Alexandria (c. 10–70 AD) is credited with Heron's formula for finding the area of a scalene triangle and with being the first to recognize the possibility of negative numbers possessing square roots. Menelaus of Alexandria
Menelaus of Alexandria
Menelaus of Alexandria was a Greek mathematician and astronomer, the first to recognize geodesics on a curved surface as natural analogs of straight lines.-Life and Works:...
(c. 100 AD) pioneered spherical trigonometry
Spherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
through Menelaus' theorem
Menelaus' theorem
Menelaus' theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, thenThis equation uses signed lengths of...
. The most complete and influential trigonometric work of antiquity is the Almagest
Almagest
The Almagest is a 2nd-century mathematical and astronomical treatise on the apparent motions of the stars and planetary paths. Written in Greek by Claudius Ptolemy, a Roman era scholar of Egypt,...
of Ptolemy (c. AD 90-168), a landmark astronomical treatise whose trigonometric tables would be used by astronomers for the next thousand years. Ptolemy is also credited with Ptolemy's theorem
Ptolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
for deriving trigonometric quantities, and the most accurate value of π outside of China until the medieval period, 3.1416.
Chinese mathematics
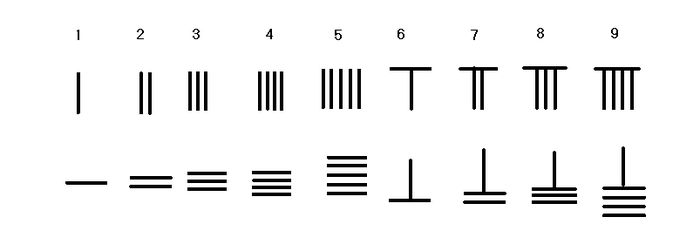
Of particular note is the use in Chinese mathematics of a decimal positional notation system, the so-called "rod numerals" in which distinct ciphers were used for numbers between 1 and 10, and additional ciphers for powers of ten. Thus, the number 123 would be written using the symbol for "1", followed by the symbol for "100", then the symbol for "2" followed by the symbol for "10", followed by the symbol for "3". This was the most advanced number system in the world at the time, apparently in use several centuries before the common era and well before the development of the Indian numeral system. Rod numerals allowed the representation of numbers as large as desired and allowed calculations to be carried out on the suan pan, or (Chinese abacus). The date of the invention of the suan pan is not certain, but the earliest written mention dates from AD 190, in Xu Yue's Supplementary Notes on the Art of Figures.
The oldest existent work on geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
in China comes from the philosophical Mohist
Mohism
Mohism or Moism was a Chinese philosophy developed by the followers of Mozi , 470 BC–c.391 BC...
canon c. 330 BC, compiled by the followers of Mozi
Mozi
Mozi |Lat.]] as Micius, ca. 470 BC – ca. 391 BC), original name Mo Di , was a Chinese philosopher during the Hundred Schools of Thought period . Born in Tengzhou, Shandong Province, China, he founded the school of Mohism, and argued strongly against Confucianism and Daoism...
(470–390 BC). The Mo Jing described various aspects of many fields associated with physical science, and provided a small number of geometrical theorems as well.
In 212 BC, the Emperor Qin Shi Huang
Qin Shi Huang
Qin Shi Huang , personal name Ying Zheng , was king of the Chinese State of Qin from 246 BC to 221 BC during the Warring States Period. He became the first emperor of a unified China in 221 BC...
(Shi Huang-ti) commanded all books in the Qin Empire other than officially sanctioned ones be burned. This decree was not universally obeyed, but as a consequence of this order little is known about ancient Chinese mathematics before this date. After the book burning
Burning of books and burying of scholars
Burning of the books and burying of the scholars is a phrase that refers to a policy and a sequence of events in the Qin Dynasty of Ancient China, between the period of 213 and 206 BC. During these events, the Hundred Schools of Thought were pruned; legalism survived...
of 212 BC, the Han dynasty
Han Dynasty
The Han Dynasty was the second imperial dynasty of China, preceded by the Qin Dynasty and succeeded by the Three Kingdoms . It was founded by the rebel leader Liu Bang, known posthumously as Emperor Gaozu of Han. It was briefly interrupted by the Xin Dynasty of the former regent Wang Mang...
(202 BC–220 AD) produced works of mathematics which presumably expanded on works that are now lost. The most important of these is The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art
The Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, the full title of which appeared by AD 179, but existed in part under other titles beforehand. It consists of 246 word problems involving agriculture, business, employment of geometry to figure height spans and dimension ratios for Chinese pagoda
Chinese pagoda
Chinese Pagodas are a traditional part of Chinese architecture. In addition to religious use, since ancient times Chinese pagodas have been praised for the spectacular views which they offer, and many famous poems in Chinese history attest to the joy of scaling pagodas.-History:The pagoda is...
towers, engineering, surveying
Surveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
, and includes material on right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s and values of π. It created mathematical proof for the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, and a mathematical formula for Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
. Liu Hui
Liu Hui
Liu Hui was a mathematician of the state of Cao Wei during the Three Kingdoms period of Chinese history. In 263, he edited and published a book with solutions to mathematical problems presented in the famous Chinese book of mathematic known as The Nine Chapters on the Mathematical Art .He was a...
commented on the work in the 3rd century AD, and gave a value of π accurate to 5 decimal places. Though more of a matter of computational stamina than theoretical insight, in the 5th century AD Zu Chongzhi
Zu Chongzhi
Zu Chongzhi , courtesy name Wenyuan , was a prominent Chinese mathematician and astronomer during the Liu Song and Southern Qi Dynasties.-Life and works:...
computed the value of π to seven decimal places, which remained the most accurate value of π for almost the next 1000 years. He also established a method which would later be called Cavalieri's principle
Cavalieri's principle
In geometry, Cavalieri's principle, sometimes called the method of indivisibles, named after Bonaventura Cavalieri, is as follows:* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that plane...
to find the volume of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
.
The high water mark of Chinese mathematics occurs in the 13th century (latter part of the Sung period), with the development of Chinese algebra. The most important text from that period is the Precious Mirror of the Four Elements by Chu Shih-chieh (fl. 1280-1303), dealing with the solution of simultaneous higher order algebraic equations using a method similar to Horner's method. The Precious Mirror also contains a diagram of Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
with coefficients of binomial expansions through the eighth power, though both appear in Chinese works as early as 1100. The Chinese also made use of the complex combinatorial diagram known as the magic square
Magic square
In recreational mathematics, a magic square of order n is an arrangement of n2 numbers, usually distinct integers, in a square, such that the n numbers in all rows, all columns, and both diagonals sum to the same constant. A normal magic square contains the integers from 1 to n2...
and magic circles
Magic circle (mathematics)
Magic circles were invented by the Song Dynasty Chinese mathematician Yang Hui . It is the arrangement of natural numbers on circles where the sum of the numbers on each circle and the sum of numbers on diameter are identical...
, described in ancient times and perfected by Yang Hui
Yang Hui
Yang Hui , courtesy name Qianguang , was a Chinese mathematician from Qiantang , Zhejiang province during the late Song Dynasty . Yang worked on magic squares, magic circles and the binomial theorem, and is best known for his contribution of presenting 'Yang Hui's Triangle'...
(AD 1238–1298).
Even after European mathematics began to flourish during the Renaissance
Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
, European and Chinese mathematics were separate traditions, with significant Chinese mathematical output in decline from the 13th century onwards. Jesuit missionaries such as Matteo Ricci
Matteo Ricci
Matteo Ricci, SJ was an Italian Jesuit priest, and one of the founding figures of the Jesuit China Mission, as it existed in the 17th-18th centuries. His current title is Servant of God....
carried mathematical ideas back and forth between the two cultures from the 16th to 18th centuries, though at this point far more mathematical ideas were entering China than leaving.
Indian mathematics
The earliest civilization on the Indian subcontinent is the Indus Valley CivilizationIndus Valley Civilization
The Indus Valley Civilization was a Bronze Age civilization that was located in the northwestern region of the Indian subcontinent, consisting of what is now mainly modern-day Pakistan and northwest India...
that flourished between 2600 and 1900 BC in the Indus river
Indus River
The Indus River is a major river which flows through Pakistan. It also has courses through China and India.Originating in the Tibetan plateau of western China in the vicinity of Lake Mansarovar in Tibet Autonomous Region, the river runs a course through the Ladakh district of Jammu and Kashmir and...
basin. Their cities were laid out with geometric regularity, but no known mathematical documents survive from this civilization.
The oldest extant mathematical records from India are the Sulba Sutras
Sulba Sutras
The Shulba Sutras or Śulbasūtras are sutra texts belonging to the Śrauta ritual and containing geometry related to fire-altar construction.- Purpose and origins :...
(dated variously between the 8th century BC and the 2nd century AD), appendices to religious texts which give simple rules for constructing altars of various shapes, such as squares, rectangles, parallelograms, and others. As with Egypt, the preoccupation with temple functions points to an origin of mathematics in religious ritual. The Sulba Sutras give methods for constructing a circle with approximately the same area as a given square
Squaring the circle
Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
, which imply several different approximations of the value of π. In addition, they compute the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of 2 to several decimal places, list Pythagorean triples, and give a statement of the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. All of these results are present in Babylonian mathematics, indicating Mesopotamian influence. It is not known to what extent the Sulba Sutras influenced later Indian mathematicians. As in China, there is a lack of continuity in Indian mathematics; significant advances are separated by long periods of inactivity.
(c. 5th century BC) formulated the rules for Sanskrit grammar
Sanskrit grammar
The grammar of the Sanskrit language has a complex verbal system, rich nominal declension, and extensive use of compound nouns. It was studied and codified by Sanskrit grammarians from the later Vedic period , culminating in the Pāṇinian grammar of the 4th century BC.-Grammatical tradition:The...
. His notation was similar to modern mathematical notation, and used metarules, transformations, and recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. Pingala
Pingala
Pingala is the traditional name of the author of the ' , the earliest known Sanskrit treatise on prosody.Nothing is known about Piṅgala himself...
(roughly 3rd-1st centuries BC) in his treatise of prosody uses a device corresponding to a binary numeral system
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
. His discussion of the combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
of meters
Metre (music)
Meter or metre is a term that music has inherited from the rhythmic element of poetry where it means the number of lines in a verse, the number of syllables in each line and the arrangement of those syllables as long or short, accented or unaccented...
corresponds to an elementary version of the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. Pingala's work also contains the basic ideas of Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s (called mātrāmeru).
The next significant mathematical documents from India after the Sulba Sutras are the Siddhantas, astronomical treatises from the 4th and 5th centuries AD (Gupta period) showing strong Hellenistic influence. They are significant in that they contain the first instance of trigonometric relations based on the half-chord, as is the case in modern trigonometry, rather than the full chord, as was the case in Ptolemaic trigonometry. Through a series of translation errors, the words "sine" and "cosine" derive from the Sanskrit "jiya" and "kojiya".
In the 5th century AD, Aryabhata
Aryabhata
Aryabhata was the first in the line of great mathematician-astronomers from the classical age of Indian mathematics and Indian astronomy...
wrote the Aryabhatiya
Aryabhatiya
Āryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
, a slim volume, written in verse, intended to supplement the rules of calculation used in astronomy and mathematical mensuration, though with no feeling for logic or deductive methodology. Though about half of the entries are wrong, it is in the Aryabhatiya that the decimal place-value system first appears. Several centuries later, the Muslim mathematician
Islamic mathematics
In the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
Abu Rayhan Biruni described the Aryabhatiya as a "mix of common pebbles and costly crystals".
In the 7th century, Brahmagupta
Brahmagupta
Brahmagupta was an Indian mathematician and astronomer who wrote many important works on mathematics and astronomy. His best known work is the Brāhmasphuṭasiddhānta , written in 628 in Bhinmal...
identified the Brahmagupta theorem
Brahmagupta theorem
Brahmagupta's theorem is a result in geometry. It states that if a cyclic quadrilateral is orthodiagonal , then the perpendicular to a side from the point of intersection of the diagonals always bisects the opposite side...
, Brahmagupta's identity and Brahmagupta's formula
Brahmagupta's formula
In Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
, and for the first time, in Brahma-sphuta-siddhanta
Brahmasphutasiddhanta
The main work of Brahmagupta, Brāhmasphuṭasiddhānta , written c.628, contains ideas including a good understanding of the mathematical role of zero, rules for manipulating both negative and positive numbers, a method for computing square roots, methods of solving linear and some quadratic...
, he lucidly explained the use of zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
as both a placeholder and decimal digit, and explained the Hindu-Arabic numeral system
Hindu-Arabic numeral system
The Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
. It was from a translation of this Indian text on mathematics (c. 770) that Islamic mathematicians were introduced to this numeral system, which they adapted as Arabic numerals
Arabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
. Islamic scholars carried knowledge of this number system to Europe by the 12th century, and it has now displaced all older number systems throughout the world. In the 10th century, Halayudha
Halayudha
Halayudha was a 10th century Indian mathematician who wrote the ', a commentary on Pingala's Chandah-shastra, containing a clear description of Pascal's triangle ....
's commentary on Pingala
Pingala
Pingala is the traditional name of the author of the ' , the earliest known Sanskrit treatise on prosody.Nothing is known about Piṅgala himself...
's work contains a study of the Fibonacci sequence and Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
, and describes the formation of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
In the 12th century, Bhāskara II lived in southern India and wrote extensively on all then known branches of mathematic. His work contains mathematical objects equivalent or approximately equivalent to infinitesimals, derivatives, the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
and the derivative of the sine function. To what extent he anticipated the invention of calculus is a controversial subject among historians of mathematics
In the 14th century, Madhava of Sangamagrama
Madhava of Sangamagrama
Mādhava of Sañgamāgrama was a prominent Kerala mathematician-astronomer from the town of Irińńālakkuţa near Cochin, Kerala, India. He is considered the founder of the Kerala School of Astronomy and Mathematics...
, the founder of the so-called Kerala School of Mathematics, found the Madhava–Leibniz series, and, using 21 terms, computed the value of π as 3.14159265359. Madhava also found the Madhava-Gregory series
Gregory's series
Gregory's series, also known as the Madhava-Gregory series or Leibniz's series, is a mathematical series that was discovered by the Indian mathematician Madhava of Sangamagrama...
to determine the arctangent, the Madhava-Newton power series to determine sine and cosine and the Taylor approximation
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for sine and cosine functions . In the 16th century, Jyesthadeva consolidated many of the Kerala School's developments and theorems in the Yukti-bhāṣā. However, the Kerala School did not formulate a systematic theory of differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
, nor is there any direct evidence of their results being transmitted outside Kerala. Progress in mathematics along with other fields of science stagnated in India with the establishment of Muslim rule in India
Muslim conquest in the Indian subcontinent
Muslim conquest in South Asia mainly took place from the 13th to the 16th centuries, though earlier Muslim conquests made limited inroads into the region, beginning during the period of the ascendancy of the Rajput Kingdoms in North India, from the 7th century onwards.However, the Himalayan...
.
Islamic mathematics
The Islamic EmpireCaliphate
The term caliphate, "dominion of a caliph " , refers to the first system of government established in Islam and represented the political unity of the Muslim Ummah...
established across Persia, the Middle East
Middle East
The Middle East is a region that encompasses Western Asia and Northern Africa. It is often used as a synonym for Near East, in opposition to Far East...
, Central Asia
Central Asia
Central Asia is a core region of the Asian continent from the Caspian Sea in the west, China in the east, Afghanistan in the south, and Russia in the north...
, North Africa
North Africa
North Africa or Northern Africa is the northernmost region of the African continent, linked by the Sahara to Sub-Saharan Africa. Geopolitically, the United Nations definition of Northern Africa includes eight countries or territories; Algeria, Egypt, Libya, Morocco, South Sudan, Sudan, Tunisia, and...
, Iberia
Iberian Peninsula
The Iberian Peninsula , sometimes called Iberia, is located in the extreme southwest of Europe and includes the modern-day sovereign states of Spain, Portugal and Andorra, as well as the British Overseas Territory of Gibraltar...
, and in parts of India
History of India
The history of India begins with evidence of human activity of Homo sapiens as long as 75,000 years ago, or with earlier hominids including Homo erectus from about 500,000 years ago. The Indus Valley Civilization, which spread and flourished in the northwestern part of the Indian subcontinent from...
in the 8th century made significant contributions towards mathematics. Although most Islamic texts on mathematics were written in Arabic
Arabic language
Arabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
, most of them were not written by Arab
Arab
Arab people, also known as Arabs , are a panethnicity primarily living in the Arab world, which is located in Western Asia and North Africa. They are identified as such on one or more of genealogical, linguistic, or cultural grounds, with tribal affiliations, and intra-tribal relationships playing...
s, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time. Persians
Persian people
The Persian people are part of the Iranian peoples who speak the modern Persian language and closely akin Iranian dialects and languages. The origin of the ethnic Iranian/Persian peoples are traced to the Ancient Iranian peoples, who were part of the ancient Indo-Iranians and themselves part of...
contributed to the world of Mathematics alongside Arabs.
In the 9th century, the Persian
Persian people
The Persian people are part of the Iranian peoples who speak the modern Persian language and closely akin Iranian dialects and languages. The origin of the ethnic Iranian/Persian peoples are traced to the Ancient Iranian peoples, who were part of the ancient Indo-Iranians and themselves part of...
mathematician wrote several important books on the Hindu-Arabic numerals and on methods for solving equations. His book On the Calculation with Hindu Numerals, written about 825, along with the work of Al-Kindi
Al-Kindi
' , known as "the Philosopher of the Arabs", was a Muslim Arab philosopher, mathematician, physician, and musician. Al-Kindi was the first of the Muslim peripatetic philosophers, and is unanimously hailed as the "father of Islamic or Arabic philosophy" for his synthesis, adaptation and promotion...
, were instrumental in spreading Indian mathematics
Indian mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...
and Indian numerals
Hindu-Arabic numeral system
The Hindu–Arabic numeral system or Hindu numeral system is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian and Arab mathematicians , and spread to the western world...
to the West. The word algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
is derived from the Latinization of his name, Algoritmi, and the word algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
from the title of one of his works, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala
The Compendious Book on Calculation by Completion and Balancing
, also known under a shorter name spelled as Hisab al-jabr w’al-muqabala, Kitab al-Jabr wa-l-Muqabala and other transliterations) is a mathematical book written in Arabic in approximately AD 820 by the Persian (Arabic for "The Compendious Book on Calculation by Completion and Balancing", in...
(The Compendious Book on Calculation by Completion and Balancing). He gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots, and he was the first to teach algebra in an elementary form
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
and for its own sake. He also discussed the fundamental method of "reduction
Reduction (mathematics)
In mathematics, reduction refers to the rewriting of an expression into a simpler form. For example, the process of rewriting a fraction into one with the smallest whole-number denominator possible is called "reducing a fraction"...
" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which al-Khwārizmī originally described as al-jabr. His algebra was also no longer concerned "with a series of problem
Problem
A problem is an obstacle, impediment, difficulty or challenge, or any situation that invites resolution; the resolution of which is recognized as a solution or contribution toward a known purpose or goal...
s to be resolved, but an exposition
Expository writing
Expository writing is a type of writing where the purpose is to inform, explain, describe, or define the author's subject to the reader. Expository text is meant to deposit information and is the most frequently used type of writing by students in colleges and universities. A well-written...
which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." He also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems."
Further developments in algebra were made by Al-Karaji
Al-Karaji
' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
in his treatise al-Fakhri, where he extends the methodology to incorporate integer powers and integer roots of unknown quantities. Something close to a proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
appears in a book written by Al-Karaji around 1000 AD, who used it to prove the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
, Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
, and the sum of integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
cubes. The historian
Historian
A historian is a person who studies and writes about the past and is regarded as an authority on it. Historians are concerned with the continuous, methodical narrative and research of past events as relating to the human race; as well as the study of all history in time. If the individual is...
of mathematics, F. Woepcke, praised Al-Karaji for being "the first who introduced the theory
Theory
The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...
of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
." Also in the 10th century, Abul Wafa
Abul Wáfa
Abū al-Wafāʾ, Muḥammad ibn Muḥammad ibn Yaḥyā ibn Ismāʿīl ibn al-ʿAbbās al-Būzjānī was a Persian mathematician and astronomer who worked in Baghdad...
translated the works of Diophantus
Diophantus
Diophantus of Alexandria , sometimes called "the father of algebra", was an Alexandrian Greek mathematician and the author of a series of books called Arithmetica. These texts deal with solving algebraic equations, many of which are now lost...
into Arabic. Ibn al-Haytham was the first mathematician to derive the formula for the sum of the fourth powers, using a method that is readily generalizable for determining the general formula for the sum of any integral powers. He performed an integration in order to find the volume of a paraboloid
Paraboloid
In mathematics, a paraboloid is a quadric surface of special kind. There are two kinds of paraboloids: elliptic and hyperbolic. The elliptic paraboloid is shaped like an oval cup and can have a maximum or minimum point....
, and was able to generalize his result for the integrals of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s up to the fourth degree. He thus came close to finding a general formula for the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s of polynomials, but he was not concerned with any polynomials higher than the fourth degree.
In the late 11th century, Omar Khayyam
Omar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
wrote Discussions of the Difficulties in Euclid, a book about what he perceived as flaws in Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, especially the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
. He was also the first to find the general geometric solution to cubic equations. He was also very influential in calendar reform
Calendar reform
A calendar reform is any significant revision of a calendar system. The term sometimes is used instead for a proposal to switch to a different calendar.Most calendars have several rules which could be altered by reform:...
.
In the 13th century, Nasir al-Din Tusi (Nasireddin) made advances in spherical trigonometry
Spherical trigonometry
Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
. He also wrote influential work on Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
. In the 15th century, Ghiyath al-Kashi computed the value of π to the 16th decimal place. Kashi also had an algorithm for calculating nth roots, which was a special case of the methods given many centuries later by Ruffini
Paolo Ruffini
Paolo Ruffini was an Italian mathematician and philosopher.By 1788 he had earned university degrees in philosophy, medicine/surgery, and mathematics...
and Horner
William George Horner
William George Horner was a British mathematician and schoolmaster. The invention of the zoetrope, in 1834 and under a different name , has been attributed to him.-Life:...
.
Other achievements of Muslim mathematicians during this period include the addition of the decimal point notation to the Arabic numerals
Arabic numerals
Arabic numerals or Hindu numerals or Hindu-Arabic numerals or Indo-Arabic numerals are the ten digits . They are descended from the Hindu-Arabic numeral system developed by Indian mathematicians, in which a sequence of digits such as "975" is read as a numeral...
, the discovery of all the modern trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s besides the sine, al-Kindi
Al-Kindi
' , known as "the Philosopher of the Arabs", was a Muslim Arab philosopher, mathematician, physician, and musician. Al-Kindi was the first of the Muslim peripatetic philosophers, and is unanimously hailed as the "father of Islamic or Arabic philosophy" for his synthesis, adaptation and promotion...
's introduction of cryptanalysis
Cryptanalysis
Cryptanalysis is the study of methods for obtaining the meaning of encrypted information, without access to the secret information that is normally required to do so. Typically, this involves knowing how the system works and finding a secret key...
and frequency analysis
Frequency analysis
In cryptanalysis, frequency analysis is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers....
, the development of analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
by Ibn al-Haytham, the beginning of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
by Omar Khayyam
Omar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
and the development of an algebraic notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
by al-Qalasādī
Abu al-Hasan ibn Ali al-Qalasadi
Abū al-Ḥasan ibn ʿAlī ibn Muḥammad ibn ʿAlī al-Qalaṣādī was a Muslim mathematician from Al-Andalus specializing in Islamic inheritance jurisprudence...
.
During the time of the Ottoman Empire
Ottoman Empire
The Ottoman EmpireIt was usually referred to as the "Ottoman Empire", the "Turkish Empire", the "Ottoman Caliphate" or more commonly "Turkey" by its contemporaries...
and Safavid Empire from the 15th century, the development of Islamic mathematics became stagnant.
Medieval European mathematics
Medieval European interest in mathematics was driven by concerns quite different from those of modern mathematicians. One driving element was the belief that mathematics provided the key to understanding the created order of nature, frequently justified by PlatoPlato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
's Timaeus
Timaeus (dialogue)
Timaeus is one of Plato's dialogues, mostly in the form of a long monologue given by the title character, written circa 360 BC. The work puts forward speculation on the nature of the physical world and human beings. It is followed by the dialogue Critias.Speakers of the dialogue are Socrates,...
and the biblical passage (in the Book of Wisdom
Book of Wisdom
The Book of Wisdom, often referred to simply as Wisdom or the Book of the Wisdom of Solomon, is one of the deuterocanonical books of the Bible. It is one of the seven Sapiential or wisdom books of the Septuagint Old Testament, which includes Job, Psalms, Proverbs, Ecclesiastes, Song of Solomon ,...
) that God had ordered all things in measure, and number, and weight.
Boethius provided a place for mathematics in the curriculum in the 6th century when he coined the term quadrivium
Quadrivium
The quadrivium comprised the four subjects, or arts, taught in medieval universities, after teaching the trivium. The word is Latin, meaning "the four ways" , and its use for the 4 subjects has been attributed to Boethius or Cassiodorus in the 6th century...
to describe the study of arithmetic, geometry, astronomy, and music. He wrote De institutione arithmetica, a free translation from the Greek of Nicomachus
Nicomachus
Nicomachus was an important mathematician in the ancient world and is best known for his works Introduction to Arithmetic and Manual of Harmonics in Greek. He was born in Gerasa, in the Roman province of Syria , and was strongly influenced by Aristotle...
's Introduction to Arithmetic; De institutione musica, also derived from Greek sources; and a series of excerpts from Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
. His works were theoretical, rather than practical, and were the basis of mathematical study until the recovery of Greek and Arabic mathematical works.
In the 12th century, European scholars traveled to Spain and Sicily seeking scientific Arabic texts, including al-Khwārizmī's The Compendious Book on Calculation by Completion and Balancing
The Compendious Book on Calculation by Completion and Balancing
, also known under a shorter name spelled as Hisab al-jabr w’al-muqabala, Kitab al-Jabr wa-l-Muqabala and other transliterations) is a mathematical book written in Arabic in approximately AD 820 by the Persian (Arabic for "The Compendious Book on Calculation by Completion and Balancing", in...
, translated into Latin by Robert of Chester
Robert of Chester
Robert of Chester was an English arabist of the 12th century. He translated several historically important books from Arabic to Latin, by authors such as Abu Musa Jabir Ibn Hayyan and Al-Khwarizmi including:...
, and the complete text of Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, translated in various versions by Adelard of Bath
Adelard of Bath
Adelard of Bath was a 12th century English scholar. He is known both for his original works and for translating many important Greek and Arabic scientific works of astrology, astronomy, philosophy and mathematics into Latin from Arabic versions, which were then introduced to Western Europe...
, Herman of Carinthia
Herman of Carinthia
Herman Dalmatin or Herman of Carinthia , also known in Latin as Sclavus Dalmata, Secundus, was a philosopher, astronomer, astrologer, mathematician, translator and author....
, and Gerard of Cremona
Gerard of Cremona
Gerard of Cremona was an Italian translator of Arabic scientific works found in the abandoned Arab libraries of Toledo, Spain....
.
These new sources sparked a renewal of mathematics. Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
, writing in the Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
, in 1202 and updated in 1254, produced the first significant mathematics in Europe since the time of Eratosthenes
Eratosthenes
Eratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...
, a gap of more than a thousand years. The work introduced Hindu-Arabic numerals to Europe, and discussed many other mathematical problems.
The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. One important contribution was development of mathematics of local motion.
Thomas Bradwardine
Thomas Bradwardine
Thomas Bradwardine was an English scholar, scientist, courtier and, very briefly, Archbishop of Canterbury. As a celebrated scholastic philosopher and doctor of theology, he is often called Doctor Profundus, .-Life:He was born either at Hartfield in Sussex or at Chichester, where his family were...
proposed that speed (V) increases in arithmetic proportion as the ratio of force (F) to resistance (R) increases in geometric proportion. Bradwardine expressed this by a series of specific examples, but although the logarithm had not yet been conceived, we can express his conclusion anachronistically by writing:
V = log (F/R). Bradwardine's analysis is an example of transferring a mathematical technique used by al-Kindi
Al-Kindi
' , known as "the Philosopher of the Arabs", was a Muslim Arab philosopher, mathematician, physician, and musician. Al-Kindi was the first of the Muslim peripatetic philosophers, and is unanimously hailed as the "father of Islamic or Arabic philosophy" for his synthesis, adaptation and promotion...
and Arnald of Villanova to quantify the nature of compound medicines to a different physical problem.
One of the 14th-century Oxford Calculators
Oxford Calculators
The Oxford Calculators were a group of 14th-century thinkers, almost all associated with Merton College, Oxford, who took a strikingly logico-mathematical approach to philosophical problems....
, William Heytesbury
William Heytesbury
William Heytesbury , philosopher and logician, is best known as one of the Oxford Calculators of Merton College, where he was a fellow by 1330....
, lacking differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
and the concept of limits
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
, proposed to measure instantaneous speed "by the path that would be described by [a body] if... it were moved uniformly at the same degree of speed with which it is moved in that given instant".
Heytesbury and others mathematically determined the distance covered by a body undergoing uniformly accelerated motion (today solved by integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
), stating that "a moving body uniformly acquiring or losing that increment [of speed] will traverse in some given time a [distance] completely equal to that which it would traverse if it were moving continuously through the same time with the mean degree [of speed]".
Nicole Oresme at the University of Paris
University of Paris
The University of Paris was a university located in Paris, France and one of the earliest to be established in Europe. It was founded in the mid 12th century, and officially recognized as a university probably between 1160 and 1250...
and the Italian Giovanni di Casali
Giovanni di Casali
Giovanni di Casali was a friar in the Franciscan Order, a natural philosopher and a theologian. He entered the order in Genoa and was lecturer in the Franciscan stadium at Assisi from 1335 to 1340. He subsequently was lector at Cambridge ca...
independently provided graphical demonstrations of this relationship, asserting that the area under the line depicting the constant acceleration, represented the total distance traveled. In a later mathematical commentary on Euclid's Elements, Oresme made a more detailed general analysis in which he demonstrated that a body will acquire in each successive increment of time an increment of any quality that increases as the odd numbers. Since Euclid had demonstrated the sum of the odd numbers are the square numbers, the total quality acquired by the body increases as the square of the time.
Renaissance mathematics

Renaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
, the development of mathematics and of accounting were intertwined. While there is no direct relationship between algebra and accounting, the teaching of the subjects and the books published often intended for the children of merchants who were sent to reckoning schools (in Flanders
Flanders
Flanders is the community of the Flemings but also one of the institutions in Belgium, and a geographical region located in parts of present-day Belgium, France and the Netherlands. "Flanders" can also refer to the northern part of Belgium that contains Brussels, Bruges, Ghent and Antwerp...
and Germany
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
) or abacus school
Abacus School
Abacus or abaco refers to calculations, especially the subject of direct calculations, using Hindu numerals without the help of the abacus . Abacus school is a term applied to any Italian school or tutorial after the 13th century, whose commerce-directed curriculum placed special emphasis on...
s (known as abbaco in Italy), where they learned the skills useful for trade and commerce. There is probably no need for algebra in performing bookkeeping
Bookkeeping
Bookkeeping is the recording of financial transactions. Transactions include sales, purchases, income, receipts and payments by an individual or organization. Bookkeeping is usually performed by a bookkeeper. Bookkeeping should not be confused with accounting. The accounting process is usually...
operations, but for complex bartering operations or the calculation of compound interest
Compound interest
Compound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding...
, a basic knowledge of arithmetic was mandatory and knowledge of algebra was very useful.
Luca Pacioli
Luca Pacioli
Fra Luca Bartolomeo de Pacioli was an Italian mathematician, Franciscan friar, collaborator with Leonardo da Vinci, and seminal contributor to the field now known as accounting...
's "Summa de Arithmetica, Geometria, Proportioni et Proportionalità" (Italian: "Review of Arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, Geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
and Proportion") was first printed and published in Venice
Venice
Venice is a city in northern Italy which is renowned for the beauty of its setting, its architecture and its artworks. It is the capital of the Veneto region...
in 1494. It included a 27-page treatise
Treatise
A treatise is a formal and systematic written discourse on some subject, generally longer and treating it in greater depth than an essay, and more concerned with investigating or exposing the principles of the subject.-Noteworthy treatises:...
on bookkeeping
Bookkeeping
Bookkeeping is the recording of financial transactions. Transactions include sales, purchases, income, receipts and payments by an individual or organization. Bookkeeping is usually performed by a bookkeeper. Bookkeeping should not be confused with accounting. The accounting process is usually...
, "Particularis de Computis et Scripturis" (Italian: "Details of Calculation and Recording"). It was written primarily for, and sold mainly to, merchants who used the book as a reference text, as a source of pleasure from the mathematical puzzles it contained, and to aid the education of their sons. In Summa Arithmetica, Pacioli introduced symbols for plus and minus for the first time in a printed book, symbols that became standard notation in Italian Renaissance mathematics. Summa Arithmetica was also the first known book printed in Italy to contain algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
. It is important to note that Pacioli himself had borrowed much of the work of Piero Della Francesca
Piero della Francesca
Piero della Francesca was a painter of the Early Renaissance. As testified by Giorgio Vasari in his Lives of the Artists, to contemporaries he was also known as a mathematician and geometer. Nowadays Piero della Francesca is chiefly appreciated for his art. His painting was characterized by its...
whom he plagiarized.
In Italy, during the first half of the 16th century, Scipione del Ferro
Scipione del Ferro
Scipione del Ferro was an Italian mathematician who first discovered a method to solve the depressed cubic equation.-Life:Scipione del Ferro was born in Bologna, in northern Italy, to Floriano and Filippa Ferro...
and Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia
Niccolò Fontana Tartaglia was a mathematician, an engineer , a surveyor and a bookkeeper from the then-Republic of Venice...
discovered solutions for cubic equations. Gerolamo Cardano
Gerolamo Cardano
Gerolamo Cardano was an Italian Renaissance mathematician, physician, astrologer and gambler...
published them in his 1545 book Ars Magna
Ars Magna (Gerolamo Cardano)
The Ars Magna is an important book on Algebra written by Gerolamo Cardano. It was first published in 1545 under the title Artis Magnæ, Sive de Regulis Algebraicis Liber Unus . There was a second edition in Cardano's lifetime, published in 1570...
, together with a solution for the quartic equations, discovered by his student Lodovico Ferrari
Lodovico Ferrari
Lodovico Ferrari was an Italian mathematician.Born in Milan, Italy, grandfather, Bartholomew Ferrari was forced out of Milan to Bologna. He settled in Bologna, Italy and he began his career as the servant of Gerolamo Cardano. He was extremely bright, so Cardano started teaching him mathematics...
. In 1572 Rafael Bombelli
Rafael Bombelli
Rafael Bombelli was an Italian mathematician.Born in Bologna, he is the author of a treatise on algebra and is a central figure in the understanding of imaginary numbers....
published his L'Algebra in which he showed how to deal with the imaginary quantities
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
that could appear in Cardano's formula for solving cubic equations.
Simon Stevin
Simon Stevin
Simon Stevin was a Flemish mathematician and military engineer. He was active in a great many areas of science and engineering, both theoretical and practical...
's book De Thiende ('the art of tenths'), first published in Dutch in 1585, contained the first systematic treatment of decimal notation, which influenced all later work on the real number system.
Driven by the demands of navigation and the growing need for accurate maps of large areas, trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
grew to be a major branch of mathematics. Bartholomaeus Pitiscus
Bartholomaeus Pitiscus
Bartholomaeus Pitiscus was a 16th century German trigonometrist, astronomer and theologian who first coined the word Trigonometry....
was the first to use the word, publishing his Trigonometria in 1595. Regiomontanus's table of sines and cosines was published in 1533.
17th century
The 17th century saw an unprecedented explosion of mathematical and scientific ideas across Europe. Galileo observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland. Tycho BraheTycho Brahe
Tycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky. Through his position as Brahe's assistant, Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
was first exposed to and seriously interacted with the topic of planetary motion. Kepler's calculations were made simpler by the contemporaneous invention of natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
s by John Napier
John Napier
John Napier of Merchiston – also signed as Neper, Nepair – named Marvellous Merchiston, was a Scottish mathematician, physicist, astronomer & astrologer, and also the 8th Laird of Merchistoun. He was the son of Sir Archibald Napier of Merchiston. John Napier is most renowned as the discoverer...
and Jost Bürgi. Kepler succeeded in formulating mathematical laws of planetary motion. The analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
developed by René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
(1596–1650) allowed those orbits to be plotted on a graph, in Cartesian coordinates. Simon Stevin
Simon Stevin
Simon Stevin was a Flemish mathematician and military engineer. He was active in a great many areas of science and engineering, both theoretical and practical...
(1585) created the basis for modern decimal notation capable of describing all numbers, whether rational or irrational.
Building on earlier work by many predecessors, Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
discovered the laws of physics explaining Kepler's Laws, and brought together the concepts now known as infinitesimal calculus
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
. Independently, Gottfried Wilhelm Leibniz developed calculus and much of the calculus notation still in use today. Science and mathematics had become an international endeavor, which would soon spread over the entire world.
In addition to the application of mathematics to the studies of the heavens, applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
began to expand into new areas, with the correspondence of Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
and Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
. Pascal and Fermat set the groundwork for the investigations of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and the corresponding rules of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
in their discussions over a game of gambling
Gambling
Gambling is the wagering of money or something of material value on an event with an uncertain outcome with the primary intent of winning additional money and/or material goods...
. Pascal, with his wager
Pascal's Wager
Pascal's Wager, also known as Pascal's Gambit, is a suggestion posed by the French philosopher, mathematician, and physicist Blaise Pascal that even if the existence of God could not be determined through reason, a rational person should wager as though God exists, because one living life...
, attempted to use the newly developing probability theory to argue for a life devoted to religion, on the grounds that even if the probability of success was small, the rewards were infinite. In some sense, this foreshadowed the development of utility theory in the 18th–19th century.
18th century

Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
. His contributions range from founding the study of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
with the Seven Bridges of Königsberg
Seven Bridges of Königsberg
The Seven Bridges of Königsberg is a historically notable problem in mathematics. Its negative resolution by Leonhard Euler in 1735 laid the foundations of graph theory and prefigured the idea of topology....
problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol i
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
, and he popularized the use of the Greek letter
 to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.
to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.Other important European mathematicians of the 18th century included Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon did important work on the foundations of celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
and on statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
.
19th century
Throughout the 19th century mathematics became increasingly abstract. In the 19th century lived Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
(1777–1855). Leaving aside his many contributions to science, in pure mathematics
Pure mathematics
Broadly speaking, pure mathematics is mathematics which studies entirely abstract concepts. From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics, and at variance with the trend towards meeting the needs of...
he did revolutionary work on function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s of complex variables, in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and on the convergence of series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
. He gave the first satisfactory proofs of the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
and of the quadratic reciprocity law.
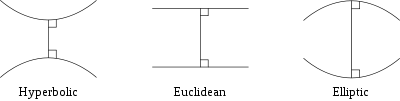
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
, where the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
of Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
no longer holds.
The Russian mathematician Nikolai Ivanovich Lobachevsky
Nikolai Ivanovich Lobachevsky
Nikolai Ivanovich Lobachevsky was a Russian mathematician and geometer, renowned primarily for his pioneering works on hyperbolic geometry, otherwise known as Lobachevskian geometry...
and his rival, the Hungarian mathematician János Bolyai
János Bolyai
János Bolyai was a Hungarian mathematician, known for his work in non-Euclidean geometry.Bolyai was born in the Transylvanian town of Kolozsvár , then part of the Habsburg Empire , the son of Zsuzsanna Benkő and the well-known mathematician Farkas Bolyai.-Life:By the age of 13, he had mastered...
, independently defined and studied hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, where uniqueness of parallels no longer holds. In this geometry the sum of angles in a triangle add up to less than 180°. Elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
was developed later in the 19th century by the German mathematician Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
; here no parallel can be found and the angles in a triangle add up to more than 180°. Riemann also developed Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, which unifies and vastly generalizes the three types of geometry, and he defined the concept of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, which generalize the ideas of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s and surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
s.
The 19th century saw the beginning of a great deal of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. Hermann Grassmann
Hermann Grassmann
Hermann Günther Grassmann was a German polymath, renowned in his day as a linguist and now also admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher...
in Germany gave a first version of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in Ireland developed noncommutative algebra. The British mathematician George Boole
George Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
devised an algebra that soon evolved into what is now called Boolean algebra
Boolean algebra
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets...
, in which the only numbers were 0 and 1. Boolean algebra is the starting point of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and has important applications in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
Augustin-Louis Cauchy, Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
, and Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
reformulated the calculus in a more rigorous fashion.
Also, for the first time, the limits of mathematics were explored. Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
, a Norwegian, and Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
, a Frenchman, proved that there is no general algebraic method for solving polynomial equations of degree greater than four (Abel–Ruffini theorem
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
). Other 19th century mathematicians utilized this in their proofs that straightedge and compass alone are not sufficient to trisect an arbitrary angle, to construct the side of a cube twice the volume of a given cube, nor to construct a square equal in area to a given circle. Mathematicians had vainly attempted to solve all of these problems since the time of the ancient Greeks. On the other hand, the limitation of three dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s in geometry was surpassed in the 19th century through considerations of parameter space
Parameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
and hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
s.
Abel and Galois's investigations into the solutions of various polynomial equations laid the groundwork for further developments of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, and the associated fields of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. In the 20th century physicists and other scientists have seen group theory as the ideal way to study symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
.
In the later 19th century, Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
established the first foundations of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, which enabled the rigorous treatment of the notion of infinity and has become the common language of nearly all mathematics. Cantor's set theory, and the rise of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
in the hands of Peano, L. E. J. Brouwer, David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
, and A.N. Whitehead, initiated a long running debate on the foundations of mathematics
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
.
The 19th century saw the founding of a number of national mathematical societies: the London Mathematical Society
London Mathematical Society
-See also:* American Mathematical Society* Edinburgh Mathematical Society* European Mathematical Society* List of Mathematical Societies* Council for the Mathematical Sciences* BCS-FACS Specialist Group-External links:* * *...
in 1865, the Société Mathématique de France
Société Mathématique de France
The Société Mathématique de France is the main professional society of French mathematicians.The society was founded in 1872 by Émile Lemoine and is one of the oldest mathematical societies in existence...
in 1872, the Circolo Mathematico di Palermo in 1884, the Edinburgh Mathematical Society
Edinburgh Mathematical Society
The Edinburgh Mathematical Society is the leading mathematical society in Scotland.The Society was founded in 1883 by a group of Edinburgh schoolteachers and academics, on the initiative of A. Y. Fraser and A. J. G. Barclay, teachers at George Watson's College and Cargill Gilston Knott, who was the...
in 1883, and the American Mathematical Society
American Mathematical Society
The American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
in 1888. The first international, special-interest society, the Quaternion Society, was formed in 1899, in the context of a vector controversy.
20th century

In a 1900 speech to the International Congress of Mathematicians
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
, David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
set out a list of 23 unsolved problems in mathematics
Hilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
. These problems, spanning many areas of mathematics, formed a central focus for much of 20th century mathematics. Today, 10 have been solved, 7 are partially solved, and 2 are still open. The remaining 4 are too loosely formulated to be stated as solved or not.
Notable historical conjectures were finally proved. In 1976, Wolfgang Haken
Wolfgang Haken
Wolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...
and Kenneth Appel
Kenneth Appel
Kenneth Ira Appel is a mathematician who in 1976, with colleague Wolfgang Haken at the University of Illinois at Urbana-Champaign, solved one of the most famous problems in mathematics, the four-color theorem...
used a computer to prove the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
. Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
, building on the work of others, proved Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
in 1995. Paul Cohen
Paul Cohen (mathematician)
Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...
and Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
proved that the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
is independent of (could neither be proved nor disproved from) the standard axioms of set theory. In 1998 Thomas Callister Hales
Thomas Callister Hales
Thomas Callister Hales is an American mathematician. He is known for his 1998 computer-aided proof of the Kepler conjecture, a centuries-old problem in discrete geometry which states that the most space-efficient way to pack spheres is in a pyramid shape...
proved the Kepler conjecture
Kepler conjecture
The Kepler conjecture, named after the 17th-century German astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic...
.
Mathematical collaborations of unprecedented size and scope took place. An example is the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
(also called the "enormous theorem"), whose proof between 1955 and 1983 required 500-odd journal articles by about 100 authors, and filling tens of thousands of pages. A group of French mathematicians, including Jean Dieudonné
Jean Dieudonné
Jean Alexandre Eugène Dieudonné was a French mathematician, notable for research in abstract algebra and functional analysis, for close involvement with the Nicolas Bourbaki pseudonymous group and the Éléments de géométrie algébrique project of Alexander Grothendieck, and as a historian of...
and André Weil
André Weil
André Weil was an influential mathematician of the 20th century, renowned for the breadth and quality of his research output, its influence on future work, and the elegance of his exposition. He is especially known for his foundational work in number theory and algebraic geometry...
, publishing under the pseudonym
Pseudonym
A pseudonym is a name that a person assumes for a particular purpose and that differs from his or her original orthonym...
"Nicolas Bourbaki
Nicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
", attempted to exposit all of known mathematics as a coherent rigorous whole. The resulting several dozen volumes has had a controversial influence on mathematical education.

General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Entire new areas of mathematics such as mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, and John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
's game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
changed the kinds of questions that could be answered by mathematical methods. All kinds of structures
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
were abstracted using axioms and given names like metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s, topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s etc. As mathematicians do, the concept of an abstract structure was itself abstracted and led to category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. Grothendieck and Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
recast algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
using sheaf theory
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
. Large advances were made in the qualitative study of dynamical systems
Dynamical systems theory
Dynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
that Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
had begun in the 1890s. Measure theory was developed in the late 19th and early 20th centuries. Applications of measures include the Lebesgue integral, Kolmogorov's axiomatisation of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, and ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
. Knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
greatly expanded. Quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
led to the development of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. Other new areas include, Laurent Schwarz's distribution theory
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, fixed point theory, singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
and René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
's catastrophe theory
Catastrophe theory
In mathematics, catastrophe theory is a branch of bifurcation theory in the study of dynamical systems; it is also a particular special case of more general singularity theory in geometry....
, model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, and Mandelbrot
Benoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
's fractals. Lie theory
Lie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
with its Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s became one of the major areas of study.
The development and continual improvement of computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s, at first mechanical analog machines and then digital electronic machines, allowed industry
Industry
Industry refers to the production of an economic good or service within an economy.-Industrial sectors:There are four key industrial economic sectors: the primary sector, largely raw material extraction industries such as mining and farming; the secondary sector, involving refining, construction,...
to deal with larger and larger amounts of data to facilitate mass production and distribution and communication, and new areas of mathematics were developed to deal with this: Alan Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
's computability theory
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
; complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
; Claude Shannon's information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
; signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
; data analysis
Data analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
; optimization and other areas of operations research
Operations research
Operations research is an interdisciplinary mathematical science that focuses on the effective use of technology by organizations...
. In the preceding centuries much mathematical focus was on calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and continuous functions, but the rise of computing and communication networks led to an increasing importance of discrete
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
concepts and the expansion of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
including graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. The speed and data processing abilities of computers also enabled the handling of mathematical problems that were too time-consuming to deal with by pencil and paper calculations, leading to areas such as numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
and symbolic computation
Symbolic computation
Symbolic computation or algebraic computation, relates to the use of machines, such as computers, to manipulate mathematical equations and expressions in symbolic form, as opposed to manipulating the approximations of specific numerical quantities represented by those symbols...
. Some of the most important methods and algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s of the 20th century are: the simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
, the Fast Fourier Transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
, error-correcting codes, the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
from control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
and the RSA algorithm of public-key cryptography
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
.
At the same time, deep insights were made about the limitations to mathematics. In 1929 and 1930, it was proved the truth or falsity of all statements formulated about the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s plus one of addition and multiplication, was decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
, i.e. could be determined by some algorithm. In 1931, Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
found that this was not the case for the natural numbers plus both addition and multiplication; this system, known as Peano arithmetic, was in fact incompletable. (Peano arithmetic is adequate for a good deal of number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, including the notion of prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
.) A consequence of Gödel's two incompleteness theorems is that in any mathematical system that includes Peano arithmetic (including all of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
), truth necessarily outruns proof, i.e. there are true statements that cannot be proved within the system. Hence mathematics cannot be reduced to mathematical logic, and David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's dream of making all of mathematics complete and consistent needed to be reformulated.
Highly composite number
A highly composite number is a positive integer with more divisors than any positive integer smaller than itself.The initial or smallest twenty-one highly composite numbers are listed in the table at right....
s, the partition function and its asymptotics, and mock theta functions
Ramanujan theta function
In mathematics, particularly q-analog theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta...
. He also made major investigations in the areas of gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
s, modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s, divergent series
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
, hypergeometric series
Hypergeometric series
In mathematics, a generalized hypergeometric series is a series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by...
and prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
theory.
Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
published more papers than any other mathematician in history, working with hundreds of collaborators. Mathematicians have a game equivalent to the Kevin Bacon Game, which leads to the Erdős number
Erdos number
The Erdős number describes the "collaborative distance" between a person and mathematician Paul Erdős, as measured by authorship of mathematical papers.The same principle has been proposed for other eminent persons in other fields.- Overview :...
of a mathematician. This describes the "collaborative distance" between a person and Paul Erdős, as measured by joint authorship of mathematical papers.
As in most areas of study, the explosion of knowledge in the scientific age has led to specialization: by the end of the century there were hundreds of specialized areas in mathematics and the Mathematics Subject Classification
Mathematics Subject Classification
The Mathematics Subject Classification is an alphanumerical classification scheme collaboratively produced by staff of and based on the coverage of the two major mathematical reviewing databases, Mathematical Reviews and Zentralblatt MATH...
was dozens of pages long. More and more mathematical journal
Mathematical journal
A mathematics journal is a scientific journal which publishes exclusively mathematics papers. A practical definition of the current state of mathematics, as a research field, is that it consists of theorems with proofs published in a reputable mathematics journal, and which usually have passed...
s were published and, by the end of the century, the development of the world wide web
World Wide Web
The World Wide Web is a system of interlinked hypertext documents accessed via the Internet...
led to online publishing.
21st century
In 2000, the Clay Mathematics InstituteClay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
announced the seven Millennium Prize Problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
, and in 2003 the Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
was solved by Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
(who declined to accept any awards).
Most mathematical journals now have online versions as well as print versions, and many online-only journals are launched. There is an increasing drive towards open access publishing, first popularized by the arXiv
ArXiv
The arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
.
Future of mathematics
There are many observable trends in mathematics, the most notable being that the subject is growing ever larger, computers are ever more important and powerful, the application of mathematics to bioinformatics is rapidly expanding, the volume of data to be analyzed being produced by science and industry, facilitated by computers, is explosively expanding.See also
- List of important publications in mathematics
- History of algebraHistory of algebraAlgebra is a branch of mathematics concerning the study of structure, relation, and quantity. Elementary algebra is the branch that deals with solving for the operands of arithmetic equations. Modern or abstract algebra has its origins as an abstraction of elementary algebra...
- History of calculusHistory of calculusCalculus, historically known as infinitesimal calculus, is a mathematical discipline focused on limits, functions, derivatives, integrals, and infinite series. Ideas leading up to the notions of function, derivative, and integral were developed throughout the 17th century, but the decisive step was...
- History of combinatoricsHistory of combinatoricsThe history of combinatorics is an area of study within the history of mathematics, dedicated to the history of combinatorics and its variations, from antiquity to modern times.-Earliest uses:The earliest books about combinatorics are from India...
- History of geometry
- History of logicHistory of logicThe history of logic is the study of the development of the science of valid inference . Formal logic was developed in ancient times in China, India, and Greece...
- History of mathematical notationHistory of mathematical notationMathematical notation comprises the symbols used to write mathematical equations and formulas. It includes Hindu-Arabic numerals, letters from the Roman, Greek, Hebrew, and German alphabets, and a host of symbols invented by mathematicians over the past several centuries.The development of...
- History of number theory
- History of statisticsHistory of statisticsThe history of statistics can be said to start around 1749 although, over time, there have been changes to the interpretation of what the word statistics means. In early times, the meaning was restricted to information about states...
- History of trigonometry
- History of writing numbers
- Kenneth O. May PrizeKenneth O. May PrizeKenneth O. May Prize and Medal in history of mathematics is an award of the International Commission on the History of Mathematics "for the encouragement and promotion of the history of mathematics internationally". It was established in 1989 and is named in honor of Kenneth O. May, the founder of...
- Timeline of mathematicsTimeline of mathematicsA timeline of pure and applied mathematics history.-Before 1000 BC:* ca. 70,000 BC — South Africa, ochre rocks adorned with scratched geometric patterns.* ca. 35,000 BC to 20,000 BC — Africa and France, earliest known prehistoric attempts to quantify time....
- prime numbers
- irrational numbers
Further reading
- Boyer, C. B.Carl Benjamin BoyerCarl Benjamin Boyer was a historian of sciences, and especially mathematics. David Foster Wallace called him the "Gibbon of math history"....
A History of Mathematics, 2nd ed. rev. by Uta C. Merzbach. New York: Wiley, 1989 ISBN 0-471-09763-2 (1991 pbk ed. ISBN 0-471-54397-7). - Eves, HowardHoward EvesHoward Whitley Eves was an American mathematician, known for his work in geometry and the history of mathematics....
, An Introduction to the History of Mathematics, Saunders, 1990, ISBN 0-03-029558-0, - Burton, David M. The History of Mathematics: An Introduction. McGraw Hill: 1997.
- Katz, Victor J. A History of Mathematics: An Introduction, 2nd Edition. Addison-WesleyAddison-WesleyAddison-Wesley was a book publisher in Boston, Massachusetts, best known for its textbooks and computer literature. As well as publishing books, Addison-Wesley also distributed its technical titles through the Safari Books Online e-reference service...
: 1998. - Kline, Morris.Morris KlineMorris Kline was a Professor of Mathematics, a writer on the history, philosophy, and teaching of mathematics, and also a popularizer of mathematical subjects.Kline grew up in Brooklyn and in Jamaica, Queens...
Mathematical Thought from Ancient to Modern Times. - Struik, D. J.Dirk Jan StruikDirk Jan Struik was a Dutch mathematician and Marxian theoretician who spent most of his life in the United States.- Life :...
(1987). A Concise History of Mathematics, fourth revised edition. Dover Publications, New York.
Books on a specific period..
- van der Waerden, B. L.Bartel Leendert van der WaerdenBartel Leendert van der Waerden was a Dutch mathematician and historian of mathematics....
, Geometry and Algebra in Ancient Civilizations, Springer, 1983, ISBN 0-387-12159-5.
Books on a specific topic
- Hoffman, Paul, The Man Who Loved Only Numbers: The Story of Paul ErdősPaul ErdosPaul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and the Search for Mathematical Truth. New York: Hyperion, 1998 ISBN 0-7868-6362-5.
Documentaries
- BBCBBCThe British Broadcasting Corporation is a British public service broadcaster. Its headquarters is at Broadcasting House in the City of Westminster, London. It is the largest broadcaster in the world, with about 23,000 staff...
(2008). The Story of MathsThe Story of MathsThe Story of Maths is a British television series outlining aspects of the history of mathematics. The series was a co-production between the Open University and the BBC and aired in October 2008 on BBC Four. The material was written and presented by Oxford professor Marcus du Sautoy...
.
External links
- MacTutor History of Mathematics archive (John J. O'Connor and Edmund F. Robertson; University of St Andrews, Scotland). An award-winning website containing detailed biographies on many historical and contemporary mathematicians, as well as information on notable curves and various topics in the history of mathematics.
- History of Mathematics Home Page (David E. Joyce; Clark University). Articles on various topics in the history of mathematics with an extensive bibliography.
- The History of Mathematics (David R. Wilkins; Trinity College, Dublin). Collections of material on the mathematics between the 17th and 19th century.
- History of Mathematics (Simon Fraser University).
- Earliest Known Uses of Some of the Words of Mathematics (Jeff Miller). Contains information on the earliest known uses of terms used in mathematics.
- Earliest Uses of Various Mathematical Symbols (Jeff Miller). Contains information on the history of mathematical notations.
- Mathematical Words: Origins and Sources (John Aldrich, University of Southampton) Discusses the origins of the modern mathematical word stock.
- Biographies of Women Mathematicians (Larry Riddle; Agnes Scott College).
- Mathematicians of the African Diaspora (Scott W. Williams; University at Buffalo).
- Fred Rickey's History of Mathematics Page
- A Bibliography of Collected Works and Correspondence of Mathematicians (Steven W. Rockey; Cornell University Library).
Organizations
Journals
- Convergence, the Mathematical Association of AmericaMathematical Association of AmericaThe Mathematical Association of America is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university, college, and high school teachers; graduate and undergraduate students; pure and applied mathematicians; computer scientists;...
's online Math History Magazine
Directories
- Links to Web Sites on the History of Mathematics (The British Society for the History of Mathematics)
- History of Mathematics Math Archives (University of Tennessee, Knoxville)
- History/Biography The Math Forum (Drexel University)
- History of Mathematics (Courtright Memorial Library).
- History of Mathematics Web Sites (David Calvis; Baldwin-Wallace College)
- Historia de las Matemáticas (Universidad de La La guna)
- História da Matemática (Universidade de Coimbra)
- Using History in Math Class
- Mathematical Resources: History of Mathematics (Bruno Kevius)
- History of Mathematics (Roberta Tucci)

