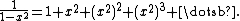Betti number
Encyclopedia
In algebraic topology
, a mathematical discipline, the Betti numbers can be used to distinguish topological space
s. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces.
Each Betti number is a natural number
or +∞
. For the most reasonable finite-dimensional spaces (such as compact
manifold
s, finite simplicial complex
es or CW complex
es), the sequence of Betti numbers is 0 from some points onwards (Betti numbers vanish above the dimension of a space), and they are all finite.
The term "Betti numbers" was coined by Henri Poincaré
after Enrico Betti
.
 Informally, the kth Betti number refers to the number of unconnected k-dimensional surfaces. The first few Betti numbers have the following intuitive definitions:
Informally, the kth Betti number refers to the number of unconnected k-dimensional surfaces. The first few Betti numbers have the following intuitive definitions:
k, the kth Betti number bk(X) of the space X is defined as the rank
of the abelian group
Hk(X), the kth homology group of X. Equivalently, one can define it as the vector space dimension of Hk(X; Q), since the homology group in this case is a vector space over Q. The universal coefficient theorem
, in a very simple case, shows that these definitions are the same.
More generally, given a field
F one can define bk(X, F), the kth Betti number with coefficients in F, as the vector space dimension of Hk(X, F).
the first Betti number of a graph G with n vertices, m edges and k connected components equals
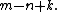
This may be proved straightforwardly by mathematical induction
on the number of edges. A new edge either increments the number of 1-cycles or decrements the number of connected components.
See cyclomatic complexity
for an application of the first Betti number in software engineering
.
in the homology groups, but they are very useful basic topological invariants. In the most intuitive terms, they allow one to count the number of holes of different dimensions. For a circle
, the first Betti number is 1. For a general pretzel, the first Betti number is twice the number of holes.
In the case of a finite simplicial complex the homology groups Hk(X, Z) are finitely-generated, and so has a finite rank. Also the group is 0 when k exceeds the top dimension of a simplex of X.
For a finite CW-complex K we have
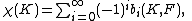
where denotes Euler characteristic
denotes Euler characteristic
of K and any field F.
For any two spaces X and Y we have
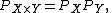
where PX denotes the Poincaré polynomial of X, (more generally, the Poincaré series
, for infinite-dimensional spaces), i.e. the
generating function
of the Betti numbers of X: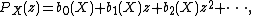
see Künneth theorem
.
If X is n-dimensional manifold, there is symmetry interchanging k and n − k, for any k:
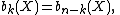
under conditions (a closed and oriented manifold); see Poincaré duality
.
The dependence on the field F is only through its characteristic. If the homology groups are torsion-free, the Betti numbers are independent of F. The connection of p-torsion and the Betti number for characteristic p, for p a prime number, is given in detail by the universal coefficient theorem
(based on Tor functors, but in a simple case).
It is possible for spaces that are infinite-dimensional in an essential way to have an infinite sequence of non-zero Betti numbers. An example is the infinite-dimensional complex projective space
, with sequence 1, 0, 1, 0, 1, ... that is periodic, with period length 2.
In this case the Poincaré function is not a polynomial but rather an infinite series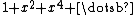 ,
,
which, being a geometric series, can be expressed as the rational function
More generally, any sequence that is periodic can be expressed as a sum of geometric series, generalizing the above (e.g.,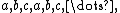 has generating function
has generating function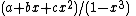 ),
),
and more generally linear recursive sequences are exactly the sequences generated by rational functions; thus the Poincaré series is expressible as a rational function if and only if the sequence of Betti numbers is a linear recursive sequence.
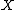 is a closed manifold
is a closed manifold
, the importance of the Betti numbers may arise from a different direction, namely that they predict the dimensions of vector spaces of closed differential forms modulo
exact differential forms. The connection with the definition given above is via three basic results, de Rham's theorem and Poincaré duality
(when those apply), and the universal coefficient theorem
of homology theory
.
There is an alternate reading, namely that the Betti numbers give the dimensions of spaces of harmonic forms. This requires also the use of some of the results of Hodge theory
, about the Hodge Laplacian.
In this setting, Morse theory
gives a set of inequalities for alternating sums of Betti numbers in terms of a corresponding alternating sum of the number of critical points
 of a Morse function of a given index
of a Morse function of a given index
:

Witten
gave an explanation of these inequalities by using the Morse function to modify the exterior derivative
in the de Rham complex.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a mathematical discipline, the Betti numbers can be used to distinguish topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces.
Each Betti number is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
or +∞
Extended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
. For the most reasonable finite-dimensional spaces (such as compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s, finite simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
es or CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es), the sequence of Betti numbers is 0 from some points onwards (Betti numbers vanish above the dimension of a space), and they are all finite.
The term "Betti numbers" was coined by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
after Enrico Betti
Enrico Betti
-External links:...
.
Informal Definition

- b0 is the number of connected components
- b1 is the number of two-dimensional or "circular" holes
- b2 is the number of three-dimensional holes or "voids"
Definition
For a non-negative integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k, the kth Betti number bk(X) of the space X is defined as the rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
of the abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
Hk(X), the kth homology group of X. Equivalently, one can define it as the vector space dimension of Hk(X; Q), since the homology group in this case is a vector space over Q. The universal coefficient theorem
Universal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
, in a very simple case, shows that these definitions are the same.
More generally, given a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F one can define bk(X, F), the kth Betti number with coefficients in F, as the vector space dimension of Hk(X, F).
Example: the first Betti number in graph theory
In topological graph theoryTopological graph theory
In mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs....
the first Betti number of a graph G with n vertices, m edges and k connected components equals
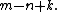
This may be proved straightforwardly by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
on the number of edges. A new edge either increments the number of 1-cycles or decrements the number of connected components.
See cyclomatic complexity
Cyclomatic complexity
Cyclomatic complexity is a software metric . It was developed by Thomas J. McCabe, Sr. in 1976 and is used to indicate the complexity of a program. It directly measures the number of linearly independent paths through a program's source code...
for an application of the first Betti number in software engineering
Software engineering
Software Engineering is the application of a systematic, disciplined, quantifiable approach to the development, operation, and maintenance of software, and the study of these approaches; that is, the application of engineering to software...
.
Properties
The (rational) Betti numbers bk(X) do not take into account any torsionTorsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
in the homology groups, but they are very useful basic topological invariants. In the most intuitive terms, they allow one to count the number of holes of different dimensions. For a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, the first Betti number is 1. For a general pretzel, the first Betti number is twice the number of holes.
In the case of a finite simplicial complex the homology groups Hk(X, Z) are finitely-generated, and so has a finite rank. Also the group is 0 when k exceeds the top dimension of a simplex of X.
For a finite CW-complex K we have
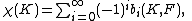
where
 denotes Euler characteristic
denotes Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of K and any field F.
For any two spaces X and Y we have
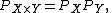
where PX denotes the Poincaré polynomial of X, (more generally, the Poincaré series
Poincaré series (modular form)
In number theory, a Poincaré series is a mathematical series generalizing the classical theta series that is associated to any discrete group of symmetries of a complex domain, possibly of several complex variables. In particular, they generalize classical Eisenstein series...
, for infinite-dimensional spaces), i.e. the
generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
of the Betti numbers of X:
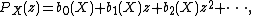
see Künneth theorem
Künneth theorem
In mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
.
If X is n-dimensional manifold, there is symmetry interchanging k and n − k, for any k:
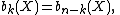
under conditions (a closed and oriented manifold); see Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
.
The dependence on the field F is only through its characteristic. If the homology groups are torsion-free, the Betti numbers are independent of F. The connection of p-torsion and the Betti number for characteristic p, for p a prime number, is given in detail by the universal coefficient theorem
Universal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
(based on Tor functors, but in a simple case).
Examples
- The Betti number sequence for a circle is 1, 1, 0, 0, 0, ...;
- the Poincaré polynomial is
 .
.
- the Poincaré polynomial is
- The Betti number sequence for a two-torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
is 1, 2, 1, 0, 0, 0, ...;- the Poincaré polynomial is
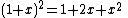 .
.
- the Poincaré polynomial is
- The Betti number sequence for a three-torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
is 1, 3, 3, 1, 0, 0, 0, ... .- the Poincaré polynomial is
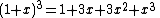 .
.
- the Poincaré polynomial is
- Similarly, for an n-torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
,- the Poincaré polynomial is
 (by the Künneth theoremKünneth theoremIn mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
(by the Künneth theoremKünneth theoremIn mathematics, especially in homological algebra and algebraic topology, a Künneth theorem is a statement relating the homology of two objects to the homology of their product. The classical statement of the Künneth theorem relates the singular homology of two topological spaces X and Y and their...
), so the Betti numbers are the binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s.
- the Poincaré polynomial is
It is possible for spaces that are infinite-dimensional in an essential way to have an infinite sequence of non-zero Betti numbers. An example is the infinite-dimensional complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, with sequence 1, 0, 1, 0, 1, ... that is periodic, with period length 2.
In this case the Poincaré function is not a polynomial but rather an infinite series
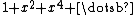 ,
,which, being a geometric series, can be expressed as the rational function
More generally, any sequence that is periodic can be expressed as a sum of geometric series, generalizing the above (e.g.,
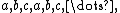 has generating function
has generating function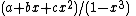 ),
),and more generally linear recursive sequences are exactly the sequences generated by rational functions; thus the Poincaré series is expressible as a rational function if and only if the sequence of Betti numbers is a linear recursive sequence.
Relationship with dimensions of spaces of differential forms
In geometric situations when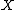 is a closed manifold
is a closed manifoldClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
, the importance of the Betti numbers may arise from a different direction, namely that they predict the dimensions of vector spaces of closed differential forms modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
exact differential forms. The connection with the definition given above is via three basic results, de Rham's theorem and Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
(when those apply), and the universal coefficient theorem
Universal coefficient theorem
In mathematics, the universal coefficient theorem in algebraic topology establishes the relationship in homology theory between the integral homology of a topological space X, and its homology with coefficients in any abelian group A...
of homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
.
There is an alternate reading, namely that the Betti numbers give the dimensions of spaces of harmonic forms. This requires also the use of some of the results of Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
, about the Hodge Laplacian.
In this setting, Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
gives a set of inequalities for alternating sums of Betti numbers in terms of a corresponding alternating sum of the number of critical points
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
 of a Morse function of a given index
of a Morse function of a given indexMorse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
:

Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
gave an explanation of these inequalities by using the Morse function to modify the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
in the de Rham complex.