|
|
|
|
Casimir effect
|
| |
|
| |
In physics, the Casimir effect and the Casimir-Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, placed a few micrometers apart, without any external electromagnetic field. In a classical description, the lack of an external field also means that there is no field between the plates, and no force would be measured between them. When this field is instead studied using quantum electrodynamics, it is seen that the plates do affect the virtual photons which constitute the field, and generate a net force—either an attraction or a repulsion depending on the specific arrangement of the two plates.
Discussion
Ask a question about 'Casimir effect' Start a new discussion about 'Casimir effect' Answer questions from other users |
Encyclopedia
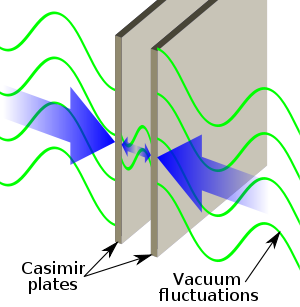
In physics, the Casimir effect and the Casimir-Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, placed a few micrometers apart, without any external electromagnetic field. In a classical description, the lack of an external field also means that there is no field between the plates, and no force would be measured between them. When this field is instead studied using quantum electrodynamics, it is seen that the plates do affect the virtual photons which constitute the field, and generate a net force—either an attraction or a repulsion depending on the specific arrangement of the two plates. This force has been measured, and is a striking example of an effect purely due to second quantization.
(However, the treatment of boundary conditions in these calculations has led to some controversy.)
Dutch physicists Hendrik B. G. Casimir and
Dirk Polder first proposed the existence of the force and formulated an experiment to detect it in 1948 while participating in research at Philips Research Labs. The classic form of the experiment, described above, successfully demonstrated the force to within 15% of the value predicted by the theory.
Because the strength of the force falls off rapidly with distance, it is only measurable when the distance between the objects is extremely small. On a submicrometre scale, this force becomes so strong that it becomes the dominant force between uncharged conductors. In fact, at separations of 10 nm—about 100 times the typical size of an atom—the Casimir effect produces the equivalent of 1 atmosphere of pressure (101.3 kPa), the precise value depending on surface geometry and other factors .
Although the Casimir effect can be expressed in terms of virtual particles interacting with the objects, it is best described and more easily calculated in terms of the zero-point energy of a quantized field in the intervening space between the objects.
In modern theoretical physics, the Casimir effect plays an important role in the chiral bag model of the nucleon; and in applied physics, it is becoming increasingly important in the development of the ever-smaller, miniaturised components of emerging microtechnologies and nanotechnologies.
Overview
The Casimir effect can be understood by the idea that the presence of conducting metals and dielectrics alter the vacuum expectation value of the energy of the second quantized electromagnetic field. Since the value of this energy depends on the shapes and positions of the conductors and dielectrics, the Casimir effect makes itself manifest as a force between such objects.
Vacuum energy
The causes of the Casimir effect are described by quantum field theory, which states that all of the various fundamental fields, such as the electromagnetic field, must be quantized at each and every point in space. In a simplified view, a "field" in physics may be envisioned as if space were filled with interconnected vibrating balls and springs, and the strength of the field can be visualized as the displacement of a ball from its rest position. Vibrations in this field propagate and are governed by the appropriate wave equation for the particular field in question. The second quantization of quantum field theory requires that each such ball-spring combination be quantized, that is, that the strength of the field be quantized at each point in space. Canonically, the field at each point in space is a simple harmonic oscillator, and its quantization places a quantum harmonic oscillator at each point. Excitations of the field correspond to the elementary particles of particle physics. 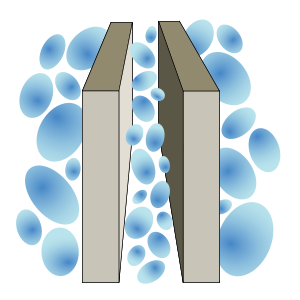However, even the vacuum has a vastly complex structure, all calculations of quantum field theory must be made in relation to this model of the vacuum.
The vacuum has, implicitly, all of the properties that a particle may have: spin, or polarization in the case of light, energy, and so on. On average, all of these properties cancel out: the vacuum is, after all, "empty" in this sense. One important exception is the vacuum energy or the vacuum expectation value of the energy. The quantization of a simple harmonic oscillator states that the lowest possible energy or zero-point energy that such an oscillator may have is
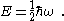
Summing over all possible oscillators at all points in space gives an infinite quantity. To remove this infinity, one may argue that only differences in energy are physically measurable; this argument is the underpinning of the theory of renormalization. In all practical calculations, this is how the infinity is always handled. In a deeper sense, however, renormalization is unsatisfying, and the removal of this infinity presents a challenge in the search for a Theory of Everything. Currently there is no compelling explanation for how this infinity should be treated as essentially zero; a non-zero value is essentially the cosmological constant and any large value causes trouble in cosmology.
The Casimir effect
Casimir's observation was that the second-quantized quantum electromagnetic field, in the presence of bulk bodies such as metals or dielectrics, must obey the same boundary conditions that the classical electromagnetic field must obey. In particular, this affects the calculation of the vacuum energy in the presence of a conductor or dielectric.
Consider, for example, the calculation of the vacuum expectation value of the electromagnetic field inside a metal cavity, such as, for example, a radar cavity or a microwave waveguide. In this case, the correct way to find the zero point energy of the field is to sum the energies of the standing waves of the cavity. To each and every possible standing wave corresponds an energy; say the energy of the nth standing wave is 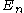. The vacuum expectation value of the energy of the electromagnetic field in the cavity is then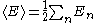
with the sum running over all possible values of n enumerating the standing waves. The factor of 1/2 corresponds to the fact that the zero-point energies are being summed (it is the same 1/2 as appears in the equation ). Written in this way, this sum is clearly divergent; however, it can be used to create finite expressions.
In particular, one may ask how the zero point energy depends on the shape s of the cavity. Each energy level 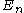depends on the shape, and so one should write 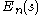for the energy level, and for the vacuum expectation value. At this point comes an important observation: the force at point p on the wall of the cavity is equal to the change in the vacuum energy if the shape s of the wall is perturbed a little bit, say by 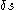, at point p. That is, one has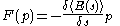
This value is finite in many practical calculations.
Casimir's calculation
In the original calculation done by Casimir, he considered the space between a pair of conducting metal plates a distance a apart. In this case, the standing waves are particularly easy to calculate, since the transverse component of the electric field and the normal component of the magnetic field must vanish on the surface of a conductor. Assuming the parallel plates lie in the x-y plane, the standing waves are
where stands for the electric component of the electromagnetic field, and, for brevity, the polarization and the magnetic components are ignored here. Here, 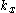and 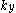are the wave vectors in directions parallel to the plates, and
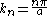
is the wave-vector perpendicular to the plates. Here, n is an integer, resulting from the requirement that ? vanish on the metal plates. The energy of this wave is
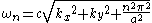
where c is the speed of light. The vacuum energy is then the sum over all possible excitation modes
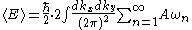
where A is the area of the metal plates, and a factor of 2 is introduced for the two possible polarizations of the wave. This expression is clearly infinite, and to proceed with the calculation, it is convenient to introduce a regulator (discussed in greater detail below). The regulator will serve to make the expression finite, and in the end will be removed. The zeta-regulated version of the energy per unit-area of the plate is
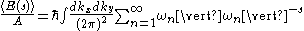
In the end, the limit 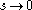is to be taken. Here s is just a complex number, not to be confused with the shape discussed previously. This integral/sum is finite for s real and larger than 3. The sum has a pole at s=3, but may be analytically continued to s=0, where the expression is finite. Expanding this, one gets
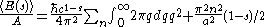
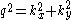where polar coordinates were introduced to turn the double integral into a single integral. The 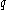in front is the Jacobian, and the 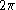comes from the angular integration. The integral is easily performed, resulting in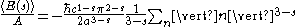
The sum may be understood to be the Riemann zeta function, and so one has
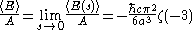
But 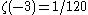and so one obtains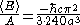
The Casimir force per unit area 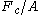for idealized, perfectly conducting plates with vacuum between them is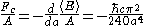
where
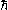(hbar, h) is the reduced Planck constant,
is the speed of light,
is the distance between the two plates.
The force is negative, indicating that the force is attractive: by moving the two plates closer together, the energy is lowered. The presence of 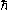shows that the Casimir force per unit area is very small, and that furthermore, the force is inherently of quantum-mechanical origin.
More recent theory
A very complete analysis of the Casimir effect at short distances is based upon a detailed analysis of the van der Waals force by Lifshitz. Using this approach, complications of the bounding surfaces, such as the modifications to the Casimir force due to finite conductivity can be calculated numerically using the tabulated complex dielectric functions of the bounding materials. In addition to these factors, complications arise due to surface roughness of the boundary and to geometry effects such as degree of parallelism of bounding plates.
For boundaries at large separations, retardation effects give rise to a long-range interaction. For the case of two parallel plates composed of ideal metals in vacuum, the results reduce to Casimir’s.
Measurement
One of the first experimental tests was conducted by Marcus Sparnaay at Philips in Eindhoven, in 1958, in a delicate and difficult experiment with parallel plates, obtaining results not in contradiction with the Casimir theory, but with large experimental errors.
The Casimir effect was measured more accurately in 1997 by Steve K. Lamoreaux of Los Alamos National Laboratory and by Umar Mohideen and Anushree Roy of the University of California at Riverside.
In practice, rather than using two parallel plates, which would require phenomenally accurate alignment to ensure they were parallel, the experiments use one plate that is flat and another plate that is a part of a sphere with a large radius. In 2001, a group at the University of Padua finally succeeded in measuring the Casimir force between parallel plates using microresonators.
Regularisation
In order to be able to perform calculations in the general case, it is convenient to introduce a regulator in the summations. This is an artificial device, used to make the sums finite so that they can be more easily manipulated, followed by the taking of a limit so as to remove the regulator.
The heat kernel or exponentially regulated sum is
where the limit 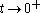is taken in the end. The divergence of the sum is typically manifested as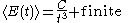
for three-dimensional cavities. The infinite part of the sum is associated with the bulk constant C which does not depend on the shape of the cavity. The interesting part of the sum is the finite part, which is shape-dependent. The Gaussian regulator
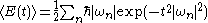
is better suited to numerical calculations because of its superior convergence properties, but is more difficult to use in theoretical calculations. Other, suitably smooth, regulators may be used as well. The zeta function regulator
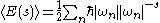
is completely unsuited for numerical calculations, but is quite useful in theoretical calculations. In particular, divergences show up as poles in the complex s plane, with the bulk divergence at s=4. This sum may be analytically continued past this pole, to obtain a finite part at s=0.
Not every cavity configuration necessarily leads to a finite part (the lack of a pole at s=0) or shape-independent infinite parts. In this case, it should be understood that additional physics has to be taken into account. In particular, at extremely large frequencies (above the plasma frequency), metals become transparent to photons (such as x-rays), and dielectrics show a frequency-dependent cutoff as well. This frequency dependence acts as a natural regulator. There are a variety of bulk effects in solid state physics, mathematically very similar to the Casimir effect, where the cutoff frequency comes into explicit play to keep expressions finite. (These are discussed in greater detail in Landau and Lifshitz, "Theory of Continuous Media".)
Generalities
The Casimir effect can also be computed using the mathematical mechanisms of functional integrals of quantum field theory, although such calculations are considerably more abstract, and thus difficult to comprehend. In addition, they can be carried out only for the simplest of geometries. However, the formalism of quantum field theory makes it clear that the vacuum expectation value summations are in a certain sense summations over so-called "virtual particles".
More interesting is the understanding that the sums over the energies of standing waves should be formally understood as sums over the eigenvalues of a Hamiltonian. This allows atomic and molecular effects, such as the van der Waals force, to be understood as a variation on the theme of the Casimir effect. Thus one considers the Hamiltonian of a system as a function of the arrangement of objects, such as atoms, in configuration space. The change in the zero-point energy as a function of changes of the configuration can be understood to result in forces acting between the objects.
In the chiral bag model of the nucleon, the Casimir energy plays an important role in showing the mass of the nucleon is independent of the bag radius. In addition, the spectral asymmetry is interpreted as a non-zero vacuum expectation value of the baryon number, cancelling the topological winding number of the pion field surrounding the nucleon.
Casimir effect and wormholes
Exotic matter with negative energy density is required to stabilize a wormhole. Morris, Thorne and Yurtsever pointed out that the quantum mechanics of the Casimir effect can be used to produce a locally mass-negative region of space-time, and suggested that negative effect could be used to stabilize a wormhole to allow faster than light travel. This concept has been used extensively in Science Fiction.
Analogies
A similar analysis can be used to explain Hawking radiation that causes the slow "evaporation" of black holes (although this is generally visualised as the escape of one particle from a virtual particle-antiparticle pair, the other particle having been captured by the black hole).
Repulsive forces
There are few instances wherein the Casimir effect can give rise to repulsive forces between uncharged objects. In a seminal paper, Evgeny Lifshitz showed (theoretically) that in certain circumstances (most commonly involving liquids), repulsive forces can arise. This has sparked interest in applications of the Casimir effect toward the development of levitating devices. Other scientists have also suggested the use of gain media to achieve a similar levitation effect, though this is controversial because these materials seem to violate fundamental causality constraints and the requirement of thermodynamic equilibrium. An experimental demonstration of the Casimir-based levitation is still yet to be made, though recent experiments involving fluids have demonstrated repulsive forces
Applications
It has been suggested that the Casimir forces have application in nanotechnology, in particular silicon integrated circuit technology based micro- and nanoelectromechanical systems, and so-called Casimir oscillators
See also
Further reading
- Introductory
- from University of California, Riverside's version of the .
- A. Lambrecht, , Physics World, September 2002.
- on Astronomy Picture of the Day
- Telegraph interviews Prof. Ulf Leonhardt and Dr Thomas Philbin
- Papers, books and lectures
- H. B. G. Casimir, and D. Polder, , Phys. Rev. 73, 360-372 (1948).
- H. B. G. Casimir, Proc. Kon. Nederland. Akad. Wetensch. B51, 793 (1948)
- S. K. Lamoreaux, "", Phys. Rev. Lett. 78, 5–8 (1997)
- M. Bordag, U. Mohideen, V.M. Mostepanenko, "", Phys. Rep. 353, 1–205 (2001), . (200+ page review paper.)
- Kimball A.Milton: "The Casimir effect", World Scientific, Singapore 2001,ISBN 981-02-4397-9
- G. Bressi, G. Carugno, R. Onofrio, G. Ruoso, "", Phys. Rev. Lett. 88 041804 (2002)
- O. Kenneth, I. Klich, A. Mann and M. Revzen, Repulsive Casimir forces, Department of Physics, Technion - Israel Institute of Technology, Haifa, February 2002
- J. D. Barrow, "", (2005) Lecture at Gresham College. (Includes discussion of French naval analogy.)
- (Also includes discussion of French naval analogy.)
- Temperature dependence
- from NIST
- V.V. Nesterenko, G. Lambiase, G. Scarpetta, , arXiv:hep-th/0503100 v2 13 May 2005
External links
- on arxiv.org
- G. Lang, web site, 2002
|
| |
|
|
