
Hawking radiation
Encyclopedia
Hawking radiation is a thermal radiation
with a black body
spectrum predicted to be emitted by black hole
s due to quantum effects. It is named after the physicist Stephen Hawking
, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist
Jacob Bekenstein
who predicted that black holes should have a finite, non-zero temperature
and entropy
. Hawking's work followed his visit to Moscow
in 1973 where Soviet scientists Yakov Zeldovich and Alexander Starobinsky showed him that according to the quantum mechanical uncertainty principle
, rotating black hole
s should create and emit particles. The Hawking radiation process reduces the mass and the energy of the black hole and is therefore also known as black hole evaporation.
Because Hawking radiation allows black holes to lose mass and energy, black holes that lose more matter than they gain through other means are expected to dissipate, shrink, and ultimately vanish. Smaller micro black hole
s (MBHs) are predicted to be larger net emitters of radiation than larger black holes; thus, they tend to shrink and dissipate faster.
Hawking's analysis became the first convincing insight into a possible theory of quantum gravity
. In September 2010, a signal which is closely related to black hole Hawking radiation (see analog gravity
) was claimed to have been observed in a laboratory experiment involving optical light pulses, however the results remain unrepeated and debated. Other projects have been launched to seek this radiation within the framework of analog gravity
. In June 2008, NASA
launched the GLAST
satellite, which will search for the terminal gamma-ray flashes expected from evaporating primordial black holes. In the very unlikely event that speculative large extra dimension
theories are correct, CERN's
Large Hadron Collider
may be able to create micro black holes and observe their evaporation.
, can escape from the black hole. It is yet unknown how gravity can be incorporated into quantum mechanics
, but nevertheless far from the black hole the gravitational effects can be weak enough for calculations to be reliably performed in the framework of quantum field theory in curved spacetime
. Hawking showed that quantum effects allow black holes to emit exact black body radiation, which is the average thermal radiation emitted by an idealized thermal source known as a black body. The electromagnetic radiation
is as if it were emitted by a black body with a temperature
that is inversely proportional
to the black hole's mass
.
Physical insight on the process may be gained by imagining that particle
-antiparticle
radiation is emitted from just beyond the event horizon
. This radiation does not come directly from the black hole itself, but rather is a result of virtual particle
s being "boosted" by the black hole's gravitation into becoming real particles.
A slightly more precise, but still much simplified, view of the process is that vacuum fluctuations cause a particle-antiparticle pair to appear close to the event horizon of a black hole. One of the pair falls into the black hole whilst the other escapes. In order to preserve total energy
, the particle that fell into the black hole must have had a negative energy (with respect to an observer far away from the black hole). By this process, the black hole loses mass, and, to an outside observer, it would appear that the black hole has just emitted a particle
. In another model, the process is a quantum tunneling effect, whereby particle-antiparticle pairs will form from the vacuum, and one will tunnel outside the event horizon.
An important difference between the black hole radiation
as computed by Hawking and thermal radiation
emitted from a black body is that the latter is statistical in nature, and only its average satisfies what is known as Planck's law of black body radiation
, while the former fits the data better. Thus thermal radiation
contains information
about the body that emitted it, while Hawking radiation seems to contain no such information, and depends only on the mass
, angular momentum
, and charge
of the black hole (the no-hair theorem). This leads to the black hole information paradox
.
However, according to the conjectured gauge-gravity duality (also known as the AdS/CFT correspondence
), black holes in certain cases (and perhaps in general) are equivalent to solutions of quantum field theory
at a non-zero temperature
. This means that no information loss is expected in black holes (since no such loss exists in the quantum field theory
), and the radiation emitted by a black hole is probably the usual thermal radiation. If this is correct, then Hawking's original calculation should be corrected, though it is not known how (see below).
For example, a black hole of one solar mass
has a temperature of only 60 nanokelvins; in fact, such a black hole would absorb far more cosmic microwave background radiation
than it emits. A black hole of 4.5 × 1022 kg (about the mass of the Moon
) would be in equilibrium at 2.7 kelvin, absorbing as much radiation as it emits. Yet smaller primordial black hole
s would emit more than they absorb, and thereby lose mass.
is the observation that Hawking's original calculation requires talking about quantum
particles in which the wavelength
becomes shorter than the Planck length near the black hole's horizon. It is due to the peculiar behavior near a gravitational horizon where time stops as measured from far away. A particle emitted from a black hole with a finite frequency
, if traced back to the horizon, must have had an infinite frequency there and a trans-Planckian wavelength.
The Unruh effect and the Hawking effect both talk about field modes in the superficially stationary space-time that change frequency relative to other coordinates which are regular across the horizon. This is necessarily so, since to stay outside a horizon requires acceleration which constantly Doppler shifts the modes.
An outgoing Hawking radiated photon
, if the mode is traced back in time, has a frequency which diverges from that which it has at great distance, as it gets closer to the horizon, which requires the wavelength of the photon to "scrunch up" infinitely at the horizon of the black hole. In a maximally extended external Schwarzschild
solution, that photon's frequency only stays regular if the mode is extended back into the past region where no observer can go. That region doesn't seem to be observable and is physically suspect, so Hawking used a black hole solution without a past region which forms at a finite time in the past. In that case, the source of all the outgoing photons can be identified–it is a microscopic point right at the moment that the black hole first formed.
The quantum
fluctuations at that tiny point, in Hawking's original calculation, contain all the outgoing radiation. The modes that eventually contain the outgoing radiation at long times are redshifted by such a huge amount by their long sojourn next to the event horizon, that they start off as modes with a wavelength much shorter than the Planck length. Since the laws of physics at such short distances are unknown, some find Hawking's original calculation unconvincing.
The trans-Planckian problem is nowadays mostly considered a mathematical artifact of horizon calculations. The same effect occurs for regular matter falling onto a white hole
solution. Matter which falls on the white hole accumulates on it, but has no future region into which it can go. Tracing the future of this matter, it is compressed onto the final singular endpoint of the white hole evolution, into a trans-Planckian region. The reason for these types of divergences is that modes which end at the horizon from the point of view of outside coordinates are singular in frequency there. The only way to determine what happens classically is to extend in some other coordinates that cross the horizon.
There exist alternative physical pictures which give the Hawking radiation in which the trans-Planckian problem is addressed. The key point is that similar trans-Planckian problems occur when the modes occupied with Unruh radiation are traced back in time. In the Unruh effect, the magnitude of the temperature can be calculated from ordinary Minkowski
field theory, and is not controversial.
applied to black hole horizons. Close to the event horizon of a black hole, a local observer must accelerate to keep from falling in. An accelerating observer sees a thermal bath of particles that pop out of the local acceleration horizon, turn around, and free-fall back in. The condition of local thermal equilibrium implies that the consistent extension of this local thermal bath has a finite temperature at infinity, which implies that some of these particles emitted by the horizon are not reabsorbed and become outgoing Hawking radiation.
A Schwarzschild black hole has a metric
The black hole is the background spacetime for a quantum field theory.
The field theory is defined by a local path integral, so if the boundary conditions at the horizon are determined, the state of the field outside will be specified. To find the appropriate boundary conditions, consider a stationary observer just outside the horizon at position . The local metric to lowest order is:
. The local metric to lowest order is:
which is Rindler in terms of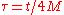 and
and  . The metric describes a frame that is accelerating to keep from falling into the black hole. The local acceleration diverges as
. The metric describes a frame that is accelerating to keep from falling into the black hole. The local acceleration diverges as  .
.
The horizon is not a special boundary, and objects can fall in. So the local observer should feel accelerated in ordinary Minkowski space by the principle of equivalence. The near-horizon observer must see the field excited at a local inverse temperature ,
,
the Unruh effect.
The gravitational redshift is by the square root of the time component of the metric. So for the field theory state to consistently extend, there must be a thermal background everywhere with the local temperature redshift-matched to the near horizon temperature: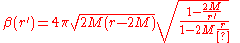
The inverse temperature redshifted to r' at infinity is
and is the near-horizon position, near 2
is the near-horizon position, near 2 , so this is really:
, so this is really:
So a field theory defined on a black hole background is in a thermal state whose temperature at infinity is:
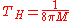
which can be expressed more cleanly in terms of the surface gravity
of the black hole, the parameter that determines the acceleration of a near-horizon observer.
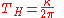
in natural units
with ,
,  ,
, 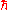 and
and 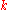 equal to 1, and where
equal to 1, and where  is the surface gravity
is the surface gravity
of the horizon. So a black hole can only be in equilibrium with a gas of radiation at a finite temperature. Since radiation incident on the black hole is absorbed, the black hole must emit an equal amount to maintain detailed balance
. The black hole acts as a perfect blackbody radiating at this temperature.
In engineering units, the radiation from a Schwarzschild
black hole is black-body radiation with temperature:

where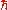 is the reduced Planck constant, c is the speed of light
is the reduced Planck constant, c is the speed of light
, kb is the Boltzmann constant, G is the gravitational constant
, and M is the mass
of the black hole.
From the black hole temperature, it is straightforward to calculate the black hole entropy. The change in entropy when a quantity of heat dQ is added is: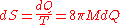
the heat energy that enters serves increase the total mass: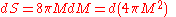 .
.
The radius of a black hole is twice its mass in natural units
, so the entropy of a black hole is proportional to its surface area: .
.
Assuming that a small black hole has zero entropy, the integration constant is zero. Forming a black hole is the most efficient way to compress mass into a region, and this entropy is also a bound on the information content of any sphere in space time. The form of the result strongly suggests that the physical description of a gravitating theory can be somehow encoded
onto a bounding surface.
E = mc²).
The power
emitted by a black hole in the form of Hawking radiation can easily be estimated for the simplest case of a nonrotating, non-charged Schwarzschild black hole of mass . Combining the formulas for the Schwarzschild radius
. Combining the formulas for the Schwarzschild radius
of the black hole, the Stefan–Boltzmann law of black-body radiation, the above formula for the temperature of the radiation, and the formula for the surface area of a sphere
(the black hole's event horizon), equation derivation:
Stefan–Boltzmann constant:
Hawking radiation temperature:
Schwarzschild radius
:
Schwarzschild sphere
surface area of Schwarzschild radius
 :
: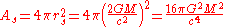
Stefan–Boltzmann power law:
A black hole is a perfect blackbody:
Stefan–Boltzmann–Schwarzschild–Hawking black hole radiation power law derivation: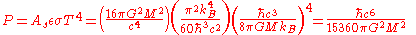
Stefan–Boltzmann-Schwarzschild-Hawking power law:
Where is the energy outflow,
is the energy outflow, 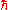 is the reduced Planck constant,
is the reduced Planck constant,  is the speed of light
is the speed of light
, and is the gravitational constant
is the gravitational constant
. It is worth mentioning that the above formula has not yet been derived in the framework of semiclassical gravity
.
The power in the Hawking radiation from a solar mass
( ) black hole turns out to be a minuscule 9 × 10−29 watts. It is indeed an extremely good approximation to call such an object 'black'.
) black hole turns out to be a minuscule 9 × 10−29 watts. It is indeed an extremely good approximation to call such an object 'black'.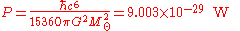
Under the assumption of an otherwise empty universe, so that no matter
or cosmic microwave background radiation
falls into the black hole, it is possible to calculate how long it would take for the black hole to dissipate:
Given that the power of the Hawking radiation is the rate of evaporation energy loss of the black hole:
Since the total energy E of the black hole is related to its mass M by Einstein's mass-energy formula: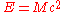

We can then equate this to our above expression for the power:
This differential equation is separable, and we can write: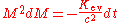
The black hole's mass is now a function M(t) of time t. Integrating over M from (the initial mass of the black hole) to zero (complete evaporation), and over t from zero to
(the initial mass of the black hole) to zero (complete evaporation), and over t from zero to  :
: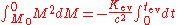
The evaporation time of a black hole is proportional to the cube of its mass:
The time that the black hole takes to dissipate is:

Where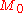 is the mass of the black hole.
is the mass of the black hole.
The lower classical quantum limit for mass for this equation is equivalent to the Planck mass,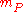 .
.
Planck mass quantum black hole Hawking radiation evaporation time: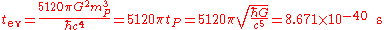
Where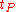 is the Planck time
is the Planck time
.
For a black hole of one solar mass
(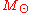 = 1.98892 × 1030 kg), we get an evaporation time of 2.098 × 1067 years—much longer than the current age of the universe
= 1.98892 × 1030 kg), we get an evaporation time of 2.098 × 1067 years—much longer than the current age of the universe
at 13.73 ± 0.12 x 109 years.
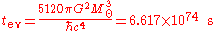
But for a black hole of 1011 kg, the evaporation time is 2.667 billion years. This is why some astronomers are searching for signs of exploding primordial black holes.
However, since the universe contains the cosmic microwave background radiation
, in order for the black hole to dissipate, it must have a temperature greater than that of the present-day black-body radiation of the universe of 2.7 K = 2.3 × 10−4 eV. This implies that must be less than 0.8% of the mass of the Earth.
must be less than 0.8% of the mass of the Earth.
In common units,

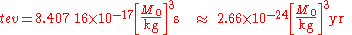
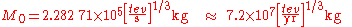
So, for instance, a 1-second-lived black hole has a mass of 2.28 × 105 kg, equivalent to an energy of 2.05 × 1022 J that could be released by 5 × 106 megatons of TNT
.
The initial power is 6.84 × 1021 W.
Black hole evaporation has several significant consequences:
In the model with large extra dimension
s, values of Planck constants can be radically different, and formulas for Hawking radiation have to be modified as well. In particular, the lifetime of a micro black hole (with radius below the scale of extra dimensions) is given by
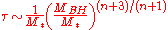
where is the low energy scale (which could be as low as a few TeV), and n is the number of large extra dimensions. This formula is now consistent with black holes as light as a few TeV, with lifetimes on the order of "new Planck time" ~10−26 s.
is the low energy scale (which could be as low as a few TeV), and n is the number of large extra dimensions. This formula is now consistent with black holes as light as a few TeV, with lifetimes on the order of "new Planck time" ~10−26 s.
. Loop-quantization reproduces the result for black hole entropy originally discovered by Bekenstein
and Hawking
. Further, it led to the computation of quantum gravity corrections to the entropy and radiation of black holes.
Based on the fluctuations of the horizon area, a quantum black hole exhibits deviations from the Hawking spectrum that would be observable were X-ray
s from Hawking radiation of evaporating primordial black holes to be observed. The deviation is such that the Hawking radiation is expected to be centered at a set of discrete and unblended energies.
s, in which sound perturbations
are analogous to light in a gravitational black hole and the flow of an approximately perfect fluid
is analogous to gravity.
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
with a black body
Black body
A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum...
spectrum predicted to be emitted by black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
s due to quantum effects. It is named after the physicist Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
Jacob Bekenstein
Jacob Bekenstein
Jacob David Bekenstein is an Israeli theoretical physicist who has contributed to the foundation of black hole thermodynamics and to other aspects of the connections between information and gravitation.-Biography:...
who predicted that black holes should have a finite, non-zero temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
. Hawking's work followed his visit to Moscow
Moscow
Moscow is the capital, the most populous city, and the most populous federal subject of Russia. The city is a major political, economic, cultural, scientific, religious, financial, educational, and transportation centre of Russia and the continent...
in 1973 where Soviet scientists Yakov Zeldovich and Alexander Starobinsky showed him that according to the quantum mechanical uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
, rotating black hole
Rotating black hole
A rotating black hole is a black hole that possesses spin angular momentum.-Types of black holes:There are four known, exact, black hole solutions to Einstein's equations, which describe gravity in General Relativity. Two of these rotate...
s should create and emit particles. The Hawking radiation process reduces the mass and the energy of the black hole and is therefore also known as black hole evaporation.
Because Hawking radiation allows black holes to lose mass and energy, black holes that lose more matter than they gain through other means are expected to dissipate, shrink, and ultimately vanish. Smaller micro black hole
Micro black hole
Micro black holes are tiny black holes, also called quantum mechanical black holes or mini black holes, for which quantum mechanical effects play an important role....
s (MBHs) are predicted to be larger net emitters of radiation than larger black holes; thus, they tend to shrink and dissipate faster.
Hawking's analysis became the first convincing insight into a possible theory of quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
. In September 2010, a signal which is closely related to black hole Hawking radiation (see analog gravity
Analog models of gravity
Analogue models of gravity is a direction of research in physics, where various phenomena of general relativity are modeled by other physical systems, such as acoustics in a moving fluid, superfluid helium, or Bose-Einstein condensate; gravity waves in water; and propagation of electromagnetic...
) was claimed to have been observed in a laboratory experiment involving optical light pulses, however the results remain unrepeated and debated. Other projects have been launched to seek this radiation within the framework of analog gravity
Analog models of gravity
Analogue models of gravity is a direction of research in physics, where various phenomena of general relativity are modeled by other physical systems, such as acoustics in a moving fluid, superfluid helium, or Bose-Einstein condensate; gravity waves in water; and propagation of electromagnetic...
. In June 2008, NASA
NASA
The National Aeronautics and Space Administration is the agency of the United States government that is responsible for the nation's civilian space program and for aeronautics and aerospace research...
launched the GLAST
Gamma-ray Large Area Space Telescope
The Fermi Gamma-ray Space Telescope , formerly referred to as the “Gamma-ray Large Area Space Telescope ”, is a space observatory being used to perform gamma-ray astronomy observations from low Earth orbit...
satellite, which will search for the terminal gamma-ray flashes expected from evaporating primordial black holes. In the very unlikely event that speculative large extra dimension
Large extra dimension
In particle physics, models with universal extra dimensions propose that there are one or more additional dimensions beyond the three spatial dimensions and one temporal dimension that are observed...
theories are correct, CERN's
CERN
The European Organization for Nuclear Research , known as CERN , is an international organization whose purpose is to operate the world's largest particle physics laboratory, which is situated in the northwest suburbs of Geneva on the Franco–Swiss border...
Large Hadron Collider
Large Hadron Collider
The Large Hadron Collider is the world's largest and highest-energy particle accelerator. It is expected to address some of the most fundamental questions of physics, advancing the understanding of the deepest laws of nature....
may be able to create micro black holes and observe their evaporation.
Overview
Black holes are sites of immense gravitational attraction. Classically, the gravitation is so powerful that nothing, not even electromagnetic radiationElectromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
, can escape from the black hole. It is yet unknown how gravity can be incorporated into quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, but nevertheless far from the black hole the gravitational effects can be weak enough for calculations to be reliably performed in the framework of quantum field theory in curved spacetime
Quantum field theory in curved spacetime
Quantum field theory in curved spacetime is an extension of standard, Minkowski-space quantum field theory to curved spacetime. A general prediction of this theory is that particles can be created by time dependent gravitational fields , or by time independent gravitational fields that contain...
. Hawking showed that quantum effects allow black holes to emit exact black body radiation, which is the average thermal radiation emitted by an idealized thermal source known as a black body. The electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
is as if it were emitted by a black body with a temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
that is inversely proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to the black hole's mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
.
Physical insight on the process may be gained by imagining that particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
-antiparticle
Antiparticle
Corresponding to most kinds of particles, there is an associated antiparticle with the same mass and opposite electric charge. For example, the antiparticle of the electron is the positively charged antielectron, or positron, which is produced naturally in certain types of radioactive decay.The...
radiation is emitted from just beyond the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
. This radiation does not come directly from the black hole itself, but rather is a result of virtual particle
Virtual particle
In physics, a virtual particle is a particle that exists for a limited time and space. The energy and momentum of a virtual particle are uncertain according to the uncertainty principle...
s being "boosted" by the black hole's gravitation into becoming real particles.
A slightly more precise, but still much simplified, view of the process is that vacuum fluctuations cause a particle-antiparticle pair to appear close to the event horizon of a black hole. One of the pair falls into the black hole whilst the other escapes. In order to preserve total energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, the particle that fell into the black hole must have had a negative energy (with respect to an observer far away from the black hole). By this process, the black hole loses mass, and, to an outside observer, it would appear that the black hole has just emitted a particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
. In another model, the process is a quantum tunneling effect, whereby particle-antiparticle pairs will form from the vacuum, and one will tunnel outside the event horizon.
An important difference between the black hole radiation
Radiation
In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...
as computed by Hawking and thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
emitted from a black body is that the latter is statistical in nature, and only its average satisfies what is known as Planck's law of black body radiation
Planck's law of black body radiation
In physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...
, while the former fits the data better. Thus thermal radiation
Thermal radiation
Thermal radiation is electromagnetic radiation generated by the thermal motion of charged particles in matter. All matter with a temperature greater than absolute zero emits thermal radiation....
contains information
Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
about the body that emitted it, while Hawking radiation seems to contain no such information, and depends only on the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, and charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
of the black hole (the no-hair theorem). This leads to the black hole information paradox
Black hole information paradox
The black hole information paradox results from the combination of quantum mechanics and general relativity. It suggests that physical information could disappear in a black hole, allowing many physical states to evolve into the same state...
.
However, according to the conjectured gauge-gravity duality (also known as the AdS/CFT correspondence
AdS/CFT correspondence
In physics, the AdS/CFT correspondence , sometimes called the Maldacena duality, is the conjectured equivalence between a string theory and gravity defined on one space, and a quantum field theory without gravity defined on the conformal boundary of this space, whose dimension is lower by one or more...
), black holes in certain cases (and perhaps in general) are equivalent to solutions of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
at a non-zero temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. This means that no information loss is expected in black holes (since no such loss exists in the quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
), and the radiation emitted by a black hole is probably the usual thermal radiation. If this is correct, then Hawking's original calculation should be corrected, though it is not known how (see below).
For example, a black hole of one solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
has a temperature of only 60 nanokelvins; in fact, such a black hole would absorb far more cosmic microwave background radiation
Cosmic microwave background radiation
In cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly....
than it emits. A black hole of 4.5 × 1022 kg (about the mass of the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
) would be in equilibrium at 2.7 kelvin, absorbing as much radiation as it emits. Yet smaller primordial black hole
Primordial black hole
A primordial black hole is a hypothetical type of black hole that is formed not by the gravitational collapse of a large star but by the extreme density of matter present during the universe's early expansion....
s would emit more than they absorb, and thereby lose mass.
Trans-Planckian problem
The trans-Planckian problemTrans-Planckian problem
In black hole physics and inflationary cosmology, the trans-Planckian problem refers to the appearance of quantities beyond the Planck scale, which raise doubts on the physical validity of some results in these two areas, since one expects the physical laws to suffer radical modifications beyond...
is the observation that Hawking's original calculation requires talking about quantum
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
particles in which the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
becomes shorter than the Planck length near the black hole's horizon. It is due to the peculiar behavior near a gravitational horizon where time stops as measured from far away. A particle emitted from a black hole with a finite frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
, if traced back to the horizon, must have had an infinite frequency there and a trans-Planckian wavelength.
The Unruh effect and the Hawking effect both talk about field modes in the superficially stationary space-time that change frequency relative to other coordinates which are regular across the horizon. This is necessarily so, since to stay outside a horizon requires acceleration which constantly Doppler shifts the modes.
An outgoing Hawking radiated photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, if the mode is traced back in time, has a frequency which diverges from that which it has at great distance, as it gets closer to the horizon, which requires the wavelength of the photon to "scrunch up" infinitely at the horizon of the black hole. In a maximally extended external Schwarzschild
Schwarzschild
Schwarzschild is a German surname meaning "black sign" or "black shield" and may refer to:* Henry Schwarzschild, , founder of NCADP, LCDC, and head of ACLU's Capital Punishment project in America...
solution, that photon's frequency only stays regular if the mode is extended back into the past region where no observer can go. That region doesn't seem to be observable and is physically suspect, so Hawking used a black hole solution without a past region which forms at a finite time in the past. In that case, the source of all the outgoing photons can be identified–it is a microscopic point right at the moment that the black hole first formed.
The quantum
Quantum
In physics, a quantum is the minimum amount of any physical entity involved in an interaction. Behind this, one finds the fundamental notion that a physical property may be "quantized," referred to as "the hypothesis of quantization". This means that the magnitude can take on only certain discrete...
fluctuations at that tiny point, in Hawking's original calculation, contain all the outgoing radiation. The modes that eventually contain the outgoing radiation at long times are redshifted by such a huge amount by their long sojourn next to the event horizon, that they start off as modes with a wavelength much shorter than the Planck length. Since the laws of physics at such short distances are unknown, some find Hawking's original calculation unconvincing.
The trans-Planckian problem is nowadays mostly considered a mathematical artifact of horizon calculations. The same effect occurs for regular matter falling onto a white hole
White hole
A white hole, in general relativity, is a hypothetical region of spacetime which cannot be entered from the outside, but from which matter and light may escape. In this sense it is the reverse of a black hole, which can be entered from the outside, but from which nothing, including light, may escape...
solution. Matter which falls on the white hole accumulates on it, but has no future region into which it can go. Tracing the future of this matter, it is compressed onto the final singular endpoint of the white hole evolution, into a trans-Planckian region. The reason for these types of divergences is that modes which end at the horizon from the point of view of outside coordinates are singular in frequency there. The only way to determine what happens classically is to extend in some other coordinates that cross the horizon.
There exist alternative physical pictures which give the Hawking radiation in which the trans-Planckian problem is addressed. The key point is that similar trans-Planckian problems occur when the modes occupied with Unruh radiation are traced back in time. In the Unruh effect, the magnitude of the temperature can be calculated from ordinary Minkowski
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
field theory, and is not controversial.
Emission process
Hawking radiation is required by the Unruh effect and the equivalence principleEquivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
applied to black hole horizons. Close to the event horizon of a black hole, a local observer must accelerate to keep from falling in. An accelerating observer sees a thermal bath of particles that pop out of the local acceleration horizon, turn around, and free-fall back in. The condition of local thermal equilibrium implies that the consistent extension of this local thermal bath has a finite temperature at infinity, which implies that some of these particles emitted by the horizon are not reabsorbed and become outgoing Hawking radiation.
A Schwarzschild black hole has a metric

The black hole is the background spacetime for a quantum field theory.
The field theory is defined by a local path integral, so if the boundary conditions at the horizon are determined, the state of the field outside will be specified. To find the appropriate boundary conditions, consider a stationary observer just outside the horizon at position
 . The local metric to lowest order is:
. The local metric to lowest order is:
which is Rindler in terms of
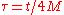 and
and  . The metric describes a frame that is accelerating to keep from falling into the black hole. The local acceleration diverges as
. The metric describes a frame that is accelerating to keep from falling into the black hole. The local acceleration diverges as  .
.The horizon is not a special boundary, and objects can fall in. So the local observer should feel accelerated in ordinary Minkowski space by the principle of equivalence. The near-horizon observer must see the field excited at a local inverse temperature
 ,
,the Unruh effect.
The gravitational redshift is by the square root of the time component of the metric. So for the field theory state to consistently extend, there must be a thermal background everywhere with the local temperature redshift-matched to the near horizon temperature:
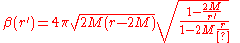
The inverse temperature redshifted to r' at infinity is

and
 is the near-horizon position, near 2
is the near-horizon position, near 2 , so this is really:
, so this is really:
So a field theory defined on a black hole background is in a thermal state whose temperature at infinity is:
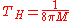
which can be expressed more cleanly in terms of the surface gravity
Surface gravity
The surface gravity, g, of an astronomical or other object is the gravitational acceleration experienced at its surface. The surface gravity may be thought of as the acceleration due to gravity experienced by a hypothetical test particle which is very close to the object's surface and which, in...
of the black hole, the parameter that determines the acceleration of a near-horizon observer.
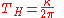
in natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
with
 ,
,  ,
, 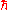 and
and 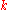 equal to 1, and where
equal to 1, and where  is the surface gravity
is the surface gravitySurface gravity
The surface gravity, g, of an astronomical or other object is the gravitational acceleration experienced at its surface. The surface gravity may be thought of as the acceleration due to gravity experienced by a hypothetical test particle which is very close to the object's surface and which, in...
of the horizon. So a black hole can only be in equilibrium with a gas of radiation at a finite temperature. Since radiation incident on the black hole is absorbed, the black hole must emit an equal amount to maintain detailed balance
Detailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
. The black hole acts as a perfect blackbody radiating at this temperature.
In engineering units, the radiation from a Schwarzschild
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
black hole is black-body radiation with temperature:

where
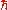 is the reduced Planck constant, c is the speed of light
is the reduced Planck constant, c is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, kb is the Boltzmann constant, G is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, and M is the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of the black hole.
From the black hole temperature, it is straightforward to calculate the black hole entropy. The change in entropy when a quantity of heat dQ is added is:
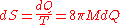
the heat energy that enters serves increase the total mass:
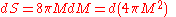 .
.The radius of a black hole is twice its mass in natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
, so the entropy of a black hole is proportional to its surface area:
 .
.Assuming that a small black hole has zero entropy, the integration constant is zero. Forming a black hole is the most efficient way to compress mass into a region, and this entropy is also a bound on the information content of any sphere in space time. The form of the result strongly suggests that the physical description of a gravitating theory can be somehow encoded
Holography
Holography is a technique that allows the light scattered from an object to be recorded and later reconstructed so that when an imaging system is placed in the reconstructed beam, an image of the object will be seen even when the object is no longer present...
onto a bounding surface.
Black hole evaporation
When particles escape, the black hole loses a small amount of its energy and therefore of its mass (mass and energy are related by Einstein's equationSpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
E = mc²).
The power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
emitted by a black hole in the form of Hawking radiation can easily be estimated for the simplest case of a nonrotating, non-charged Schwarzschild black hole of mass
 . Combining the formulas for the Schwarzschild radius
. Combining the formulas for the Schwarzschild radiusSchwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
of the black hole, the Stefan–Boltzmann law of black-body radiation, the above formula for the temperature of the radiation, and the formula for the surface area of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
(the black hole's event horizon), equation derivation:
Stefan–Boltzmann constant:

Hawking radiation temperature:
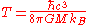 |
Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
:

Schwarzschild sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
surface area of Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
 :
: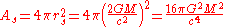
Stefan–Boltzmann power law:

A black hole is a perfect blackbody:

Stefan–Boltzmann–Schwarzschild–Hawking black hole radiation power law derivation:
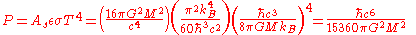
Stefan–Boltzmann-Schwarzschild-Hawking power law:
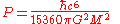 |
Where
 is the energy outflow,
is the energy outflow, 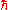 is the reduced Planck constant,
is the reduced Planck constant,  is the speed of light
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, and
 is the gravitational constant
is the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
. It is worth mentioning that the above formula has not yet been derived in the framework of semiclassical gravity
Semiclassical gravity
Semiclassical gravity is the approximation to the theory of quantum gravity in which one treats matter fields as being quantum and the gravitational field as being classical....
.
The power in the Hawking radiation from a solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
(
 ) black hole turns out to be a minuscule 9 × 10−29 watts. It is indeed an extremely good approximation to call such an object 'black'.
) black hole turns out to be a minuscule 9 × 10−29 watts. It is indeed an extremely good approximation to call such an object 'black'.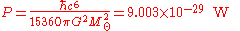
Under the assumption of an otherwise empty universe, so that no matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
or cosmic microwave background radiation
Cosmic microwave background radiation
In cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly....
falls into the black hole, it is possible to calculate how long it would take for the black hole to dissipate:

Given that the power of the Hawking radiation is the rate of evaporation energy loss of the black hole:

Since the total energy E of the black hole is related to its mass M by Einstein's mass-energy formula:
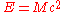

We can then equate this to our above expression for the power:

This differential equation is separable, and we can write:
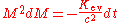
The black hole's mass is now a function M(t) of time t. Integrating over M from
 (the initial mass of the black hole) to zero (complete evaporation), and over t from zero to
(the initial mass of the black hole) to zero (complete evaporation), and over t from zero to  :
: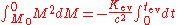
The evaporation time of a black hole is proportional to the cube of its mass:

The time that the black hole takes to dissipate is:
 |

Where
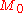 is the mass of the black hole.
is the mass of the black hole.The lower classical quantum limit for mass for this equation is equivalent to the Planck mass,
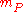 .
.Planck mass quantum black hole Hawking radiation evaporation time:
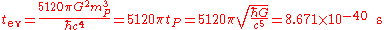
 |
Where
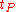 is the Planck time
is the Planck timePlanck time
In physics, the Planck time, , is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length...
.
For a black hole of one solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
(
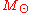 = 1.98892 × 1030 kg), we get an evaporation time of 2.098 × 1067 years—much longer than the current age of the universe
= 1.98892 × 1030 kg), we get an evaporation time of 2.098 × 1067 years—much longer than the current age of the universeBig Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
at 13.73 ± 0.12 x 109 years.
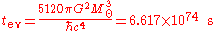
But for a black hole of 1011 kg, the evaporation time is 2.667 billion years. This is why some astronomers are searching for signs of exploding primordial black holes.
However, since the universe contains the cosmic microwave background radiation
Cosmic microwave background radiation
In cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly....
, in order for the black hole to dissipate, it must have a temperature greater than that of the present-day black-body radiation of the universe of 2.7 K = 2.3 × 10−4 eV. This implies that
 must be less than 0.8% of the mass of the Earth.
must be less than 0.8% of the mass of the Earth.In common units,

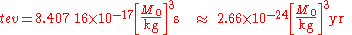
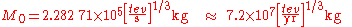
So, for instance, a 1-second-lived black hole has a mass of 2.28 × 105 kg, equivalent to an energy of 2.05 × 1022 J that could be released by 5 × 106 megatons of TNT
TNT equivalent
TNT equivalent is a method of quantifying the energy released in explosions. The ton of TNT is a unit of energy equal to 4.184 gigajoules, which is approximately the amount of energy released in the detonation of one ton of TNT...
.
The initial power is 6.84 × 1021 W.
Black hole evaporation has several significant consequences:
- Black hole evaporation produces a more consistent view of black hole thermodynamicsBlack hole thermodynamicsIn physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons...
, by showing how black holes interact thermally with the rest of the universe. - Unlike most objects, a black hole's temperature increases as it radiates away mass. The rate of temperature increase is exponential, with the most likely endpoint being the dissolution of the black hole in a violent burst of gamma rayGamma rayGamma radiation, also known as gamma rays or hyphenated as gamma-rays and denoted as γ, is electromagnetic radiation of high frequency . Gamma rays are usually naturally produced on Earth by decay of high energy states in atomic nuclei...
s. A complete description of this dissolution requires a model of quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
, however, as it occurs when the black hole approaches Planck mass and Planck radius. - The simplest models of black hole evaporation lead to the black hole information paradoxBlack hole information paradoxThe black hole information paradox results from the combination of quantum mechanics and general relativity. It suggests that physical information could disappear in a black hole, allowing many physical states to evolve into the same state...
. The information content of a black hole appears to be lost when it dissipates, as under these models the Hawking radiation is random (it has no relation to the original information). A number of solutions to this problem have been proposed, including suggestions that Hawking radiation is perturbed to contain the missing information, that the Hawking evaporation leaves some form of remnant particle containing the missing information, and that information is allowed to be lost under these conditions.
Large extra dimensions
Formulae from the previous section are only applicable if laws of gravity are approximately valid all the way down to the Planck scale. In particular, for black holes with masses below Planck mass (~10−5 g), they result in unphysical lifetimes below Planck time (~10−43 s). This is normally seen as an indication that Planck mass is the lower limit on the mass of a black hole.In the model with large extra dimension
Large extra dimension
In particle physics, models with universal extra dimensions propose that there are one or more additional dimensions beyond the three spatial dimensions and one temporal dimension that are observed...
s, values of Planck constants can be radically different, and formulas for Hawking radiation have to be modified as well. In particular, the lifetime of a micro black hole (with radius below the scale of extra dimensions) is given by
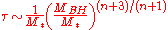
where
 is the low energy scale (which could be as low as a few TeV), and n is the number of large extra dimensions. This formula is now consistent with black holes as light as a few TeV, with lifetimes on the order of "new Planck time" ~10−26 s.
is the low energy scale (which could be as low as a few TeV), and n is the number of large extra dimensions. This formula is now consistent with black holes as light as a few TeV, with lifetimes on the order of "new Planck time" ~10−26 s.Deviation from Hawking radiation in loop quantum gravity
A detailed study of the quantum geometry of a black hole horizon has been made using loop quantum gravityLoop quantum gravity
Loop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
. Loop-quantization reproduces the result for black hole entropy originally discovered by Bekenstein
Jacob Bekenstein
Jacob David Bekenstein is an Israeli theoretical physicist who has contributed to the foundation of black hole thermodynamics and to other aspects of the connections between information and gravitation.-Biography:...
and Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
. Further, it led to the computation of quantum gravity corrections to the entropy and radiation of black holes.
Based on the fluctuations of the horizon area, a quantum black hole exhibits deviations from the Hawking spectrum that would be observable were X-ray
X-ray
X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
s from Hawking radiation of evaporating primordial black holes to be observed. The deviation is such that the Hawking radiation is expected to be centered at a set of discrete and unblended energies.
Experimental observation of Hawking radiation
Under experimentally achievable conditions for gravitational systems this effect is too small to be observed directly. However, a recent experimental set-up created a laboratory "white hole event horizon" that the experimenters claimed was shown to radiate Hawking radiation. Some scientists predict that Hawking radiation could be studied by analogy using sonic black holeSonic black hole
A sonic black hole is a phenomenon in which phonons are unable to escape from a fluid that is flowing more quickly than the local speed of sound. They are called sonic, or acoustic, black holes because these trapped phonons are analogous to light in astrophysical black holes...
s, in which sound perturbations
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
are analogous to light in a gravitational black hole and the flow of an approximately perfect fluid
Perfect fluid
In physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
is analogous to gravity.
See also
- Black hole information paradoxBlack hole information paradoxThe black hole information paradox results from the combination of quantum mechanics and general relativity. It suggests that physical information could disappear in a black hole, allowing many physical states to evolve into the same state...
- Black hole thermodynamicsBlack hole thermodynamicsIn physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons...
- Trans-Planckian problemTrans-Planckian problemIn black hole physics and inflationary cosmology, the trans-Planckian problem refers to the appearance of quantities beyond the Planck scale, which raise doubts on the physical validity of some results in these two areas, since one expects the physical laws to suffer radical modifications beyond...
- Quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
Further reading
→ Hawking's first article on the topic → first detailed studies of the evaporation mechanism → links between primordial black holes and the early universe → experimental searches for primordial black holes thanks to the emitted antimatter → cosmology with primordial black holes → searches for new physics (quantum gravity) with primordial black holes → evaporating black holes and extra-dimensions- D. Ida, K.-y. Oda & S.C.Park, Phys. Rev. D67 (2003) 064025,Phys. Rev. D71 (2005) 124039,http://arxiv.org/abs/hep-th/0602188: determination of black hole's life and extra-dimensions
- N. Nicolaevici, J. Phys. A: Math. Gen. 36 (2003) 7667-7677 http://www.iop.org/EJ/abstract/0305-4470/36/27/317/: consistent derivation of the Hawking radiation in the Fulling-Davies mirror model.
- L. Smolin, Quantum gravity faces reality, consists of the recent developments and predictions of loop quantum gravityLoop quantum gravityLoop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
about gravity in small scales including the deviation from Hawking radiation effect by Ansari Spectroscopy of a canonically quantized horizon. - M. Ansari, Area, ladder symmetry, degeneracy and fluctuations of a horizon studies the deviation of a loop quantized black hole from Hawking radiation. A novel observable quantum effect of black hole quantization is introduced.
- Stuart L. Shapiro, Saul A. Teukolsky (1983), Black holes, white dwarfs, and neutron stars: The physics of compact objects. p. 366 Wiley-Interscience, Hawking radiation evaporation formula derivation.
External links
- Hawking radiation calculator tool
- The case for mini black holes A. Barrau & J. grain explain how the Hawking radiation could be detected at colliders
- University of Colorado at Boulder
- Hawking radiation on arxiv.org
- Hawking radiation observed in laboratory?

