Zeta function regularization
Encyclopedia
In mathematics
and theoretical physics
, zeta function regularization is a type of regularization
or summability method that assigns finite values to divergent sums or products, and in particular can be used to define determinants and traces of some self-adjoint operator
s. The technique is now commonly applied to problems in physics, but has its origins in attempts to give precise meanings to ill-conditioned sums appearing in number theory
.
One method is to define its zeta regularized sum to be ζA(−1) if this is defined, where the zeta function is defined for Re(s) large by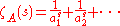
if this sum converges, and by analytic continuation elsewhere. In the case when an = n the zeta function is the ordinary Riemann zeta function, and this method was used by Euler to "sum" the series 1 + 2 + 3 + 4 + ... to ζ(−1) = −1/12.
Another method defines the possibly divergent infinite product a1a2.... to be exp(−ζ′A(0)). used this to define the determinant of a positive self-adjoint operator A (the Laplacian of a Riemannian manifold in their application) with eigenvalues a1, a2, ...., and in this case the zeta function is formally the trace of A−s. suggested using this idea to evaluate path integrals in curved spacetimes.
showed that if A is the Laplacian of a compact Riemannian manifold then the Minakshisundaram–Pleijel zeta function converges and has an analytic continuation as a meromorphic function to all complex numbers, and extended this to elliptic pseudo-differential operators A on compact Riemannian manifolds. So for such operators one can define the determinant using zeta function regularization.
of the energy
of a particle field in quantum field theory
. More generally, the zeta-function approach can be used to regularize the whole energy-momentum tensor in curved spacetime.
The unregulated value of the energy is given by a summation over the zero-point energy
of all of the excitation modes of the vacuum:
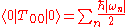
Here,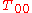
is the zero'th component of the energy-momentum tensor and the sum (which may be an integral) is understood to extend over all (positive and negative) energy modes 
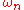; the absolute value reminding us that the energy is taken to be positive. This sum, as written, is usually infinite (
is typically linear in n). The sum may be regularized
by writing it as
where s is some parameter, taken to be a complex number
. For large, real
s greater than 4 (for three-dimensional space), the sum is manifestly finite, and thus may often be evaluated theoretically.
Such a sum will typically have a pole at s = 4, due to the bulk contributions of the quantum field in three space dimensions. However, it may be analytically continued
to s=0 where hopefully there is no pole, thus giving a finite value to the expression. A detailed example of this regularization at work is given in the article on the Casimir effect
, where the resulting sum is very explicitly the Riemann zeta-function.
The zeta-regularization is useful as it can often be used in a way such that the various symmetries of the physical system are preserved. Besides the Casimir effect, zeta-function regularization is used in conformal field theory
, renormalization
and in fixing the critical spacetime
dimension of string theory
.
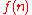. Such sums are known as Dirichlet series. The regularized form
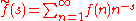
converts divergences of the sum into simple poles on the complex s-plane. In numerical calculations, the zeta-function regularization is inappropriate, as it is extremely slow to converge. For numerical purposes, a more rapidly converging sum is the exponential regularization, given by
This is sometimes called the Z-transform
of f, where z = exp(−t). The analytic structure of the exponential and zeta-regularizations are related. By expanding the exponential sum as a Laurent series
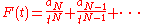
one finds that the zeta-series has the structure
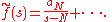
The structure of the exponential and zeta-regulators are related by means of the Mellin transform
. The one may be converted to the other by making use of the integral representation of the Gamma function
:
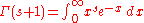
which lead to the identity
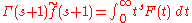
relating the exponential and zeta-regulators, and converting poles in the s-plane to divergent terms in the Laurent series.
is sometimes called a heat kernel or a heat-kernel regularized sum; this name stems from the idea that the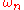
can sometimes be understood as eigenvalues of the heat kernel
. In mathematics, such a sum is known as a generalized Dirichlet series; its use for averaging is known as an Abelian mean. It is closely related to the Laplace–Stieltjes transform, in that
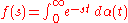
where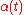
is a step function
, with steps of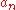
at 
. A number of theorems for the convergence of such a series exist. For example, by the Hardy-Littlewood tauberian theorem, if
then the series for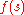
converges in the half-plane 
and is uniformly convergent on every compact subset of the half-plane 
. In almost all applications to physics, one has 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, zeta function regularization is a type of regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
or summability method that assigns finite values to divergent sums or products, and in particular can be used to define determinants and traces of some self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s. The technique is now commonly applied to problems in physics, but has its origins in attempts to give precise meanings to ill-conditioned sums appearing in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
Definition
There are several different summation methods called zeta function regularization for defining the sum of a possibly divergent series a1 + a2 + ....One method is to define its zeta regularized sum to be ζA(−1) if this is defined, where the zeta function is defined for Re(s) large by
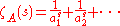
if this sum converges, and by analytic continuation elsewhere. In the case when an = n the zeta function is the ordinary Riemann zeta function, and this method was used by Euler to "sum" the series 1 + 2 + 3 + 4 + ... to ζ(−1) = −1/12.
Another method defines the possibly divergent infinite product a1a2.... to be exp(−ζ′A(0)). used this to define the determinant of a positive self-adjoint operator A (the Laplacian of a Riemannian manifold in their application) with eigenvalues a1, a2, ...., and in this case the zeta function is formally the trace of A−s. suggested using this idea to evaluate path integrals in curved spacetimes.
showed that if A is the Laplacian of a compact Riemannian manifold then the Minakshisundaram–Pleijel zeta function converges and has an analytic continuation as a meromorphic function to all complex numbers, and extended this to elliptic pseudo-differential operators A on compact Riemannian manifolds. So for such operators one can define the determinant using zeta function regularization.
Example
An example of zeta-function regularization is the calculation of the vacuum expectation valueVacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of a particle field in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. More generally, the zeta-function approach can be used to regularize the whole energy-momentum tensor in curved spacetime.
The unregulated value of the energy is given by a summation over the zero-point energy
Zero-point energy
Zero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature...
of all of the excitation modes of the vacuum:
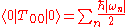
Here,
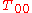is the zero'th component of the energy-momentum tensor and the sum (which may be an integral) is understood to extend over all (positive and negative) energy modes 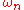; the absolute value reminding us that the energy is taken to be positive. This sum, as written, is usually infinite ( is typically linear in n). The sum may be regularizedRegularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
by writing it as
where s is some parameter, taken to be a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. For large, real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s greater than 4 (for three-dimensional space), the sum is manifestly finite, and thus may often be evaluated theoretically.
Such a sum will typically have a pole at s = 4, due to the bulk contributions of the quantum field in three space dimensions. However, it may be analytically continued
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to s=0 where hopefully there is no pole, thus giving a finite value to the expression. A detailed example of this regularization at work is given in the article on the Casimir effect
Casimir effect
In quantum field theory, the Casimir effect and the Casimir–Polder force are physical forces arising from a quantized field. The typical example is of two uncharged metallic plates in a vacuum, like capacitors placed a few micrometers apart, without any external electromagnetic field...
, where the resulting sum is very explicitly the Riemann zeta-function.
The zeta-regularization is useful as it can often be used in a way such that the various symmetries of the physical system are preserved. Besides the Casimir effect, zeta-function regularization is used in conformal field theory
Conformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
, renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
and in fixing the critical spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
dimension of string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
.
Relation to other regularizations
Zeta-function regularization gives a nice analytic structure to any sums over an arithmetic functionArithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
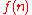. Such sums are known as Dirichlet series. The regularized form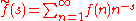converts divergences of the sum into simple poles on the complex s-plane. In numerical calculations, the zeta-function regularization is inappropriate, as it is extremely slow to converge. For numerical purposes, a more rapidly converging sum is the exponential regularization, given by
This is sometimes called the Z-transform
Z-transform
In mathematics and signal processing, the Z-transform converts a discrete time-domain signal, which is a sequence of real or complex numbers, into a complex frequency-domain representation....
of f, where z = exp(−t). The analytic structure of the exponential and zeta-regularizations are related. By expanding the exponential sum as a Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
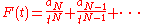
one finds that the zeta-series has the structure
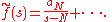
The structure of the exponential and zeta-regulators are related by means of the Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
. The one may be converted to the other by making use of the integral representation of the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
:
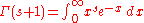
which lead to the identity
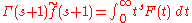
relating the exponential and zeta-regulators, and converting poles in the s-plane to divergent terms in the Laurent series.
Heat kernel regularization
The sumis sometimes called a heat kernel or a heat-kernel regularized sum; this name stems from the idea that the
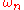can sometimes be understood as eigenvalues of the heat kernelHeat kernel
In the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a particular domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some...
. In mathematics, such a sum is known as a generalized Dirichlet series; its use for averaging is known as an Abelian mean. It is closely related to the Laplace–Stieltjes transform, in that
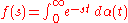
where
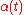is a step functionStep function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
, with steps of
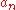at . A number of theorems for the convergence of such a series exist. For example, by the Hardy-Littlewood tauberian theorem, if then the series for
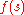converges in the half-plane and is uniformly convergent on every compact subset of the half-plane . In almost all applications to physics, one has History
Much of the early work establishing the convergence and equivalence of series regularized with the heat kernel and zeta function regularization methods was done by G.H. Hardy and J. E. Littlewood in 1916 and is based on the application of the Cahen–Mellin integral. The effort was made in order to obtain values for various ill-defined, conditionally convergent sums appearing in number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
See also
- Generating functionGenerating functionIn mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
- Perron's formulaPerron's formulaIn mathematics, and more particularly in analytic number theory, Perron's formula is a formula due to Oskar Perron to calculate the sum of an arithmetical function, by means of an inverse Mellin transform.-Statement:...
- RenormalizationRenormalizationIn quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
- 1 + 1 + 1 + 1 + · · ·