Weyl group
Encyclopedia
In mathematics
, in particular the theory of Lie algebra
s, the Weyl group of a root system
Φ is a subgroup
of the isometry
group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplane
s orthogonal to the roots, and as such is a finite reflection group. Abstractly, Weyl groups are finite Coxeter groups, and are important examples of these.
The Weyl group of a semi-simple Lie group
, a semi-simple Lie algebra
, a semi-simple linear algebraic group
, etc. is the Weyl group of the root system of that group or algebra.
It is named after Hermann Weyl
of order
12. It is isomorphic to S3, the symmetric group
generated by the three reflections on the main diagonals of the hexagon.
into a finite number of open regions, called Weyl chambers. These are permuted by the action of the Weyl group, and it is a theorem that this action is simply transitive
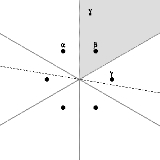
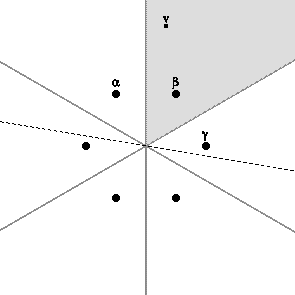
. In particular, the number of Weyl chambers equals the order of the Weyl group. Any non-zero vector v divides the Euclidean space into two half-spaces bounding the hyperplane v∧ orthogonal to v, namely v+ and v−. If v belongs to some Weyl chamber, no root lies in v∧, so every root lies in v+ or v−, and if α lies in one then −α lies in the other. Thus Φ+ := Φ∩v+ consists of exactly half of the roots of Φ. Of course, Φ+ depends on v, but it does not change if v stays in the same Weyl chamber. The base of the root system with respect to the choice Φ+ is the set of simple roots in Φ+, i.e., roots which cannot be written as a sum of two roots in Φ+. Thus, the Weyl chambers, the set Φ+, and the base determine one another, and the Weyl group acts simply transitively in each case. The following illustration shows the six Weyl chambers of the root system A2, a choice of v, the hyperplane v∧ (indicated by a dotted line), and positive roots α, β, and γ. The base in this case is {α,γ}.
Concretely, being a Coxeter group means that a Weyl group has a special kind of presentation
in which each generator xi is of order two, and the relations other than xi2 are of the form (xixj)mij. The generators are the reflections given by simple roots, and mij is 2, 3, 4, or 6 depending on whether roots i and j make an angle of 90, 120, 135, or 150 degrees, i.e., whether in the Dynkin diagram they are unconnected, connected by a simple edge, connected by a double edge, or connected by a triple edge.
Weyl groups have a Bruhat order
and length function
in terms of this presentation: the length of a Weyl group element is the length of the shortest word representing that element in terms of these standard generators. There is a unique longest element of a Coxeter group
, which is opposite to the identity in the Bruhat order.
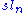is just the symmetric group
on
elements, 
. The action can be realized as follows. If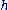 
is the Cartan subalgebra of all diagonal matrices with trace zero, then Sn acts on 
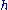via conjugation by permutation matrices
. This action induces an action on the dual space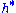
, which is the required Weyl group action.
, etc.), and a specific realization depends on a choice – of Cartan subalgebra for a Lie algebra, of maximal torus
for a Lie group. The Weyl groups of a Lie group and its corresponding Lie algebra are isomorphic, and indeed a choice of maximal torus gives a choice of Cartan subalgebra.
For a Lie algebra, the Weyl group is the reflection group generated by reflections in the roots – the specific realization of the root system depending on a choice of Cartan subalgebra (maximal abelian).
For a Lie group G satisfying certain conditions,Different conditions are sufficient – most simply if G is connected and either compact, or an affine algebraic group. The definition is simpler for a semisimple (or more generally reductive) Lie group over an algebraically closed field
, but a relative Weyl group can be defined for a split Lie group. given a torus
(which need not be maximal), the Weyl group with respect to that torus is defined as the quotient of the normalizer of the torus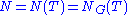 
by the centralizer of the torus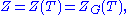 
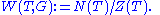
The group W is finite – Z is of finite index
in N. If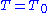
is a maximal torus
(so it equals its own centralizer: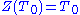
) then the resulting quotient 
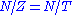is called the Weyl group of G, and denoted 
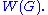Note that the specific quotient set depends on a choice of maximal torus
, but the resulting groups are all isomorphic (by an inner automorphism of G), since maximal tori are conjugate. However, the isomorphism is not natural, and depends on the choice of conjugation.
For example, for the general linear group GL, a maximal torus is the subgroup D of invertible diagonal matrices, whose normalizer is the generalized permutation matrices (matrices in the form of permutation matrices, but with any non-zero numbers in place of the '1's), and whose Weyl group is the symmetric group
. In this case the quotient map
splits (via the permutation matrices), so the normalizer N is a semidirect product
of the torus and the Weyl group, and the Weyl group can be expressed as a subgroup of G. In general this is not always the case – the quotient does not always split, the normalizer N is not always the semidirect product
of N and Z, and the Weyl group cannot always be realized as a subgroup of G.
of G, i.e., a maximal connected
solvable
subgroup and a maximal torus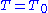
is chosen to lie in B, then we obtain the Bruhat decomposition
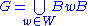
which gives rise to the decomposition of the flag variety G/B into Schubert cells (see Grassmannian
).
The structure of the Hasse diagram
of the group is related geometrically to the cohomology of the manifold (rather, of the real and complex forms of the group), which is constrained by Poincaré duality
. Thus algebraic properties of the Weyl group correspond to general topological properties of manifolds. For instance, Poincaré duality gives a pairing between cells in dimension k and in dimension
(where n is the dimension of a manifold): the bottom (0) dimensional cell corresponds to the identity element of the Weyl group, and the dual top-dimensional cell corresponds to the longest element of a Coxeter group
.
s and Weyl groups – for instance, the number of elements of the symmetric group is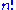
, and the number of elements of the general linear group over a finite field is the q-factorial 
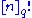; thus the symmetric group behaves as though it were a linear group over "the field with one element". This is formalized by the field with one element
, which considers Weyl groups to be simple algebraic groups over the field with one element.
of the Weyl group W with coefficients in the maximal torus T used to define it,W acts on T – that is how it is defined – and the group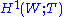
means "with respect to this action". is related to the outer automorphism group
of the normalizer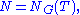
as: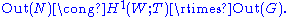
The outer automorphisms of the group Out(G) are essentially the diagram automorphisms of the Dynkin diagram, while the group cohomology is computed in and is a finite elementary abelian 2-group (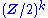
); for simple Lie groups it has order 1, 2, or 4. The 0th and 2nd group cohomology are also closely related to the normalizer.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular the theory of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, the Weyl group of a root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
Φ is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s orthogonal to the roots, and as such is a finite reflection group. Abstractly, Weyl groups are finite Coxeter groups, and are important examples of these.
The Weyl group of a semi-simple Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, a semi-simple Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, a semi-simple linear algebraic group
Linear algebraic group
In mathematics, a linear algebraic group is a subgroup of the group of invertible n×n matrices that is defined by polynomial equations...
, etc. is the Weyl group of the root system of that group or algebra.
It is named after Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
Examples
For example, the root system of A2 consists of the vertices of a regular hexagon centered at the origin. The Weyl group of this root system is a subgroup of index two of the dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
12. It is isomorphic to S3, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
generated by the three reflections on the main diagonals of the hexagon.
Weyl chambers
Removing the hyperplanes defined by the roots of Φ cuts up Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
into a finite number of open regions, called Weyl chambers. These are permuted by the action of the Weyl group, and it is a theorem that this action is simply transitive
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. In particular, the number of Weyl chambers equals the order of the Weyl group. Any non-zero vector v divides the Euclidean space into two half-spaces bounding the hyperplane v∧ orthogonal to v, namely v+ and v−. If v belongs to some Weyl chamber, no root lies in v∧, so every root lies in v+ or v−, and if α lies in one then −α lies in the other. Thus Φ+ := Φ∩v+ consists of exactly half of the roots of Φ. Of course, Φ+ depends on v, but it does not change if v stays in the same Weyl chamber. The base of the root system with respect to the choice Φ+ is the set of simple roots in Φ+, i.e., roots which cannot be written as a sum of two roots in Φ+. Thus, the Weyl chambers, the set Φ+, and the base determine one another, and the Weyl group acts simply transitively in each case. The following illustration shows the six Weyl chambers of the root system A2, a choice of v, the hyperplane v∧ (indicated by a dotted line), and positive roots α, β, and γ. The base in this case is {α,γ}.
Coxeter group structure
Weyl groups are examples of finite reflection groups, as they are generated by reflections; the abstract groups (not considered as subgroups of a linear group) are accordingly finite Coxeter groups, which allows them to be classified by their Coxeter–Dynkin diagram.Concretely, being a Coxeter group means that a Weyl group has a special kind of presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
in which each generator xi is of order two, and the relations other than xi2 are of the form (xixj)mij. The generators are the reflections given by simple roots, and mij is 2, 3, 4, or 6 depending on whether roots i and j make an angle of 90, 120, 135, or 150 degrees, i.e., whether in the Dynkin diagram they are unconnected, connected by a simple edge, connected by a double edge, or connected by a triple edge.
Weyl groups have a Bruhat order
Bruhat order
In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
and length function
Length function
In mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
in terms of this presentation: the length of a Weyl group element is the length of the shortest word representing that element in terms of these standard generators. There is a unique longest element of a Coxeter group
Longest element of a Coxeter group
In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
, which is opposite to the identity in the Bruhat order.
Example
The Weyl group of the Lie algebra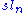 is just the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on
elements, . The action can be realized as follows. If 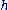is the Cartan subalgebra of all diagonal matrices with trace zero, then Sn acts on 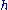via conjugation by permutation matricesPermutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
. This action induces an action on the dual space
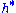, which is the required Weyl group action.Definition
The Weyl group can be defined in various ways, depending on context (Lie algebra, Lie group, symmetric spaceSymmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
, etc.), and a specific realization depends on a choice – of Cartan subalgebra for a Lie algebra, of maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
for a Lie group. The Weyl groups of a Lie group and its corresponding Lie algebra are isomorphic, and indeed a choice of maximal torus gives a choice of Cartan subalgebra.
For a Lie algebra, the Weyl group is the reflection group generated by reflections in the roots – the specific realization of the root system depending on a choice of Cartan subalgebra (maximal abelian).
For a Lie group G satisfying certain conditions,Different conditions are sufficient – most simply if G is connected and either compact, or an affine algebraic group. The definition is simpler for a semisimple (or more generally reductive) Lie group over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, but a relative Weyl group can be defined for a split Lie group. given a torus
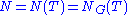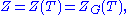
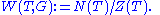
(which need not be maximal), the Weyl group with respect to that torus is defined as the quotient of the normalizer of the torus by the centralizer of the torus The group W is finite – Z is of finite index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
in N. If
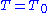is a maximal torusMaximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
(so it equals its own centralizer:
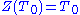) then the resulting quotient 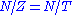is called the Weyl group of G, and denoted 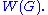Note that the specific quotient set depends on a choice of maximal torusTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, but the resulting groups are all isomorphic (by an inner automorphism of G), since maximal tori are conjugate. However, the isomorphism is not natural, and depends on the choice of conjugation.
For example, for the general linear group GL, a maximal torus is the subgroup D of invertible diagonal matrices, whose normalizer is the generalized permutation matrices (matrices in the form of permutation matrices, but with any non-zero numbers in place of the '1's), and whose Weyl group is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
. In this case the quotient map
splits (via the permutation matrices), so the normalizer N is a semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of the torus and the Weyl group, and the Weyl group can be expressed as a subgroup of G. In general this is not always the case – the quotient does not always split, the normalizer N is not always the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of N and Z, and the Weyl group cannot always be realized as a subgroup of G.
Bruhat decomposition
If B is a Borel subgroupBorel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
of G, i.e., a maximal connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
subgroup and a maximal torus
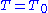is chosen to lie in B, then we obtain the Bruhat decompositionBruhat decomposition
In mathematics, the Bruhat decomposition G = BWB into cells can be regarded as a general expression of the principle of Gauss–Jordan elimination, which generically writes a matrix as a product of an upper triangular and lower triangular matrices—but with exceptional cases...
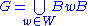
which gives rise to the decomposition of the flag variety G/B into Schubert cells (see Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
).
The structure of the Hasse diagram
Hasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
of the group is related geometrically to the cohomology of the manifold (rather, of the real and complex forms of the group), which is constrained by Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
. Thus algebraic properties of the Weyl group correspond to general topological properties of manifolds. For instance, Poincaré duality gives a pairing between cells in dimension k and in dimension
(where n is the dimension of a manifold): the bottom (0) dimensional cell corresponds to the identity element of the Weyl group, and the dual top-dimensional cell corresponds to the longest element of a Coxeter groupLongest element of a Coxeter group
In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
.
Analogy with algebraic groups
There are a number of analogous results between algebraic groupAlgebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s and Weyl groups – for instance, the number of elements of the symmetric group is
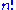, and the number of elements of the general linear group over a finite field is the q-factorial 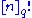; thus the symmetric group behaves as though it were a linear group over "the field with one element". This is formalized by the field with one elementField with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
, which considers Weyl groups to be simple algebraic groups over the field with one element.
Cohomology
For a non-abelian connected compact Lie group G, the first group cohomologyGroup cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
of the Weyl group W with coefficients in the maximal torus T used to define it,W acts on T – that is how it is defined – and the group
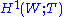means "with respect to this action". is related to the outer automorphism groupOuter automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of the normalizer
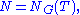as: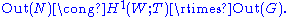The outer automorphisms of the group Out(G) are essentially the diagram automorphisms of the Dynkin diagram, while the group cohomology is computed in and is a finite elementary abelian 2-group (
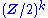); for simple Lie groups it has order 1, 2, or 4. The 0th and 2nd group cohomology are also closely related to the normalizer.