
Algebraically closed field
Encyclopedia
In mathematics
, a field
F is said to be algebraically closed if every polynomial
with one variable
of degree
at least 1, with coefficient
s in F, has a root in F.
s is not algebraically closed, because the polynomial equation x2 + 1 = 0 has no solution in real numbers, even though all its coefficients (1 and 0) are real. The same argument proves that no subfield of the real field is algebraically closed; in particular, the field of rational number
s is not algebraically closed. Also, no finite field
F is algebraically closed, because if a1, a2, …, an are the elements of F, then the polynomial (x − a1)(x − a2) ··· (x − an) + 1
has no zero in F. By contrast, the fundamental theorem of algebra
states that the field of complex number
s is algebraically closed. Another example of an algebraically closed field is the field of (complex) algebraic number
s.
s in the polynomial ring
F[x] are those of degree one.
The assertion “the polynomials of degree one are irreducible” is trivially true for any field. If F is algebraically closed and p(x) is an irreducible polynomial of F[x], then it has some root a and therefore p(x) is a multiple of x − a. Since p(x) is irreducible, this means that p(x) = k(x − a), for some k ∈ F \ {0}. On the other hand, if F is not algebraically closed, then there is some non-constant polynomial p(x) in F[x] without roots in F. Let q(x) be some irreducible factor of p(x). Since p(x) has no roots in F, q(x) also has no roots in F. Therefore, q(x) has degree greater than one, since every first degree polynomial has one root in F.
s in F, splits into linear factors
. In other words, there are elements k, x1, x2, …, xn of the field F such that p(x) = k(x − x1)(x − x2) ··· (x − xn).
If F has this property, then clearly every non-constant polynomial in F[x] has some root in F; in other words, F is algebraically closed. On the other hand, that the property stated here holds for F if F is algebraically closed follows from the previous property together with the fact that, for any field K, any polynomial in K[x] can be written as a product of irreducible polynomials.
.
If F has no proper algebraic extension, let p(x) be some irreducible polynomial in F[x]. Then the quotient
of F[x] modulo the ideal
generated by p(x) is an algebraic extension of F whose degree
is equal to the degree of p(x). Since it is not a proper extension, its degree is 1 and therefore the degree of p(x) is 1.
On the other hand, if F has some proper algebraic extension K, then the minimal polynomial
of an element in K \ F is irreducible and its degree is greater than 1.
because if, within the previous proof, the word “algebraic” is replaced by the word “finite”, then the proof is still valid.
An endomorphism of Fn has an eigenvector if and only if its characteristic polynomial
has some root. Therefore, when F is algebraically closed, every endomorphism of Fn has some eigenvector. On the other hand, if every endomorphism of Fn has an eigenvector, let p(x) be an element of F[x]. Dividing by its leading coefficient, we get another polynomial q(x) which has roots if and only if p(x) has roots. But if q(x) = xn + an − 1xn − 1+ ··· + a0, then q(x) is the characteristic polynomial of the companion matrix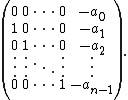
in one variable x, with coefficients in F, can be written as the sum of a polynomial function with rational functions of the form a/(x − b)n, where n is a natural number, and a and b are elements of F.
If F is algebraically closed then, since the irreducible polynomials in F[x] are all of degree 1, the property stated above holds by the theorem on partial fraction decomposition.
On the other hand, suppose that the property stated above holds for the field F. Let p(x) be an irreducible element in F[x]. Then the rational function 1/p can be written as the sum of a polynomial function q with rational functions of the form a/(x − b)n. Therefore, the rational expression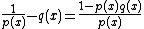
can be written as a quotient of two polynomials in which the denominator is a product of first degree polynomials. Since p(x) is irreducible, it must divide this product and, therefore, it must also be a first degree polynomial.
then they don't have a common root, for if a ∈ F was a common root, then p(x) and q(x) would both be multiples of x − a and therefore they would not relatively prime. The fields for which the reverse implication holds (that is, the fields such that whenever two polynomials have no common root then they are relatively prime) are precisely the algebraically closed fields.
If the field F is algebraically closed, let p(x) and q(x) two polynomials which are not relatively prime and let r(x) be their greatest common divisor
. Then, since r(x) is not constant, it will have some root a, which will be then a common root of p(x) and q(x).
If F is not algebraically closed, let p(x) be a polynomial whose degree is at least 1 without roots. Then p(x) and p(x) are not relatively prime, but they have no common roots (since none of them has roots).
If a proposition which can be expressed in the language of first-order logic
is true for an algebraically closed field, then it is true for every algebraically closed field with the same characteristic
. Furthermore, if such a proposition is valid for an algebraically closed field with characteristic 0, then not only is it valid for all other algebraically closed fields with characteristic 0, but there is some natural number N such that the proposition is valid for every algebraically closed field with characteristic p when p > N.
Every field F has some extension which is algebraically closed. Among all such extensions there is one and (up to isomorphism
) only one which is an algebraic extension
of F; it is called the algebraic closure
of F.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F is said to be algebraically closed if every polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with one variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
of degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
at least 1, with coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s in F, has a root in F.
Examples
As an example, the field of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s is not algebraically closed, because the polynomial equation x2 + 1 = 0 has no solution in real numbers, even though all its coefficients (1 and 0) are real. The same argument proves that no subfield of the real field is algebraically closed; in particular, the field of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s is not algebraically closed. Also, no finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
F is algebraically closed, because if a1, a2, …, an are the elements of F, then the polynomial (x − a1)(x − a2) ··· (x − an) + 1
has no zero in F. By contrast, the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
states that the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s is algebraically closed. Another example of an algebraically closed field is the field of (complex) algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s.
Equivalent properties
Given a field F, the assertion “F is algebraically closed” is equivalent to other assertions:The only irreducible polynomials are those of degree one
The field F is algebraically closed if and only if the only irreducible polynomialIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
s in the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
F[x] are those of degree one.
The assertion “the polynomials of degree one are irreducible” is trivially true for any field. If F is algebraically closed and p(x) is an irreducible polynomial of F[x], then it has some root a and therefore p(x) is a multiple of x − a. Since p(x) is irreducible, this means that p(x) = k(x − a), for some k ∈ F \ {0}. On the other hand, if F is not algebraically closed, then there is some non-constant polynomial p(x) in F[x] without roots in F. Let q(x) be some irreducible factor of p(x). Since p(x) has no roots in F, q(x) also has no roots in F. Therefore, q(x) has degree greater than one, since every first degree polynomial has one root in F.
Every polynomial is a product of first degree polynomials
The field F is algebraically closed if and only if every polynomial p(x) of degree n ≥ 1, with coefficientCoefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s in F, splits into linear factors
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
. In other words, there are elements k, x1, x2, …, xn of the field F such that p(x) = k(x − x1)(x − x2) ··· (x − xn).
If F has this property, then clearly every non-constant polynomial in F[x] has some root in F; in other words, F is algebraically closed. On the other hand, that the property stated here holds for F if F is algebraically closed follows from the previous property together with the fact that, for any field K, any polynomial in K[x] can be written as a product of irreducible polynomials.
Polynomials of prime degree have roots
J. Shipman showed in 2007 that if every polynomial over F of prime degree has a root in F, then every non-constant polynomial has a root in F, thus F is algebraically closed.The field has no proper algebraic extension
The field F is algebraically closed if and only if it has no proper algebraic extensionAlgebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
.
If F has no proper algebraic extension, let p(x) be some irreducible polynomial in F[x]. Then the quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of F[x] modulo the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by p(x) is an algebraic extension of F whose degree
Degree of a field extension
In mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
is equal to the degree of p(x). Since it is not a proper extension, its degree is 1 and therefore the degree of p(x) is 1.
On the other hand, if F has some proper algebraic extension K, then the minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
of an element in K \ F is irreducible and its degree is greater than 1.
The field has no proper finite extension
The field F is algebraically closed if and only if it has no finite algebraic extensionAlgebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
because if, within the previous proof, the word “algebraic” is replaced by the word “finite”, then the proof is still valid.
Every endomorphism of Fn has some eigenvector
The field F is algebraically closed if and only if, for each natural number n, every linear map from Fn into itself has some eigenvector.An endomorphism of Fn has an eigenvector if and only if its characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
has some root. Therefore, when F is algebraically closed, every endomorphism of Fn has some eigenvector. On the other hand, if every endomorphism of Fn has an eigenvector, let p(x) be an element of F[x]. Dividing by its leading coefficient, we get another polynomial q(x) which has roots if and only if p(x) has roots. But if q(x) = xn + an − 1xn − 1+ ··· + a0, then q(x) is the characteristic polynomial of the companion matrix
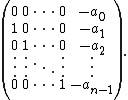
Decomposition of rational expressions
The field F is algebraically closed if and only if every rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
in one variable x, with coefficients in F, can be written as the sum of a polynomial function with rational functions of the form a/(x − b)n, where n is a natural number, and a and b are elements of F.
If F is algebraically closed then, since the irreducible polynomials in F[x] are all of degree 1, the property stated above holds by the theorem on partial fraction decomposition.
On the other hand, suppose that the property stated above holds for the field F. Let p(x) be an irreducible element in F[x]. Then the rational function 1/p can be written as the sum of a polynomial function q with rational functions of the form a/(x − b)n. Therefore, the rational expression
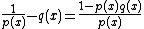
can be written as a quotient of two polynomials in which the denominator is a product of first degree polynomials. Since p(x) is irreducible, it must divide this product and, therefore, it must also be a first degree polynomial.
Relatively prime polynomials and roots
For any field F, if two polynomials p(x),q(x) ∈ F[x] are relatively primeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
then they don't have a common root, for if a ∈ F was a common root, then p(x) and q(x) would both be multiples of x − a and therefore they would not relatively prime. The fields for which the reverse implication holds (that is, the fields such that whenever two polynomials have no common root then they are relatively prime) are precisely the algebraically closed fields.
If the field F is algebraically closed, let p(x) and q(x) two polynomials which are not relatively prime and let r(x) be their greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
. Then, since r(x) is not constant, it will have some root a, which will be then a common root of p(x) and q(x).
If F is not algebraically closed, let p(x) be a polynomial whose degree is at least 1 without roots. Then p(x) and p(x) are not relatively prime, but they have no common roots (since none of them has roots).
Other properties
If F is an algebraically closed field and n is a natural number, then F contains all nth roots of unity, because these are (by definition) the n (not necessarily distinct) zeroes of the polynomial xn − 1. A field extension that is contained in an extension generated by the roots of unity is a cyclotomic extension, and the extension of a field generated by all roots of unity is sometimes called its cyclotomic closure. Thus algebraically closed fields are cyclotomically closed. The converse is not true. Even assuming that every polynomial of the form xn − a splits into linear factors is not enough to assure that the field is algebraically closed.If a proposition which can be expressed in the language of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
is true for an algebraically closed field, then it is true for every algebraically closed field with the same characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
. Furthermore, if such a proposition is valid for an algebraically closed field with characteristic 0, then not only is it valid for all other algebraically closed fields with characteristic 0, but there is some natural number N such that the proposition is valid for every algebraically closed field with characteristic p when p > N.
Every field F has some extension which is algebraically closed. Among all such extensions there is one and (up to isomorphism
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
) only one which is an algebraic extension
Algebraic extension
In abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
of F; it is called the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of F.

