Field with one element
Encyclopedia
In mathematics
, the field with one element is a suggestive name for an object that should behave similarly to a finite field
with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun. The name "field with one element" and the notation F1 are only suggestive, as there is no field with one element in classical abstract algebra
. Instead, F1 refers to the idea that there should be a way to replace sets and operations, the traditional building blocks for abstract algebra, with other, more flexible objects. While there is still no field with a single element in these theories, there is a field-like object whose characteristic
is one. This object is denoted F1.
F1 cannot be a field because all fields must contain two distinct elements, the additive identity
zero and the multiplicative identity one. Even if this restriction is dropped, a ring with one element must be the trivial ring, which does not behave like a finite field. Instead, most proposed theories of F1 replace abstract algebra entirely. Mathematical objects such as vector space
s and polynomial ring
s can be carried over into these new theories by mimicking their abstract properties. This allows the development of commutative algebra
and algebraic geometry
on new foundations. One of the defining features of theories of F1 is that these new foundations allow more objects than classical abstract algebra, one of which behaves like a field of characteristic one.
The possibility of studying the mathematics of F1 was originally suggested in 1956 by Jacques Tits
, published in , on the basis of an analogy between symmetries in projective geometry
and the combinatorics of simplicial complex
es. F1 has been connected to noncommutative geometry
and to a possible proof of the Riemann hypothesis
. Many theories of F1 have been proposed, but it is not clear which, if any, of them give F1 all the desired properties.
s to abstract simplicial complex
es. One of the assumptions is a non-triviality condition: If the building is an n-dimensional abstract simplicial complex, and if , then every k-simplex of the building must be contained in at least three n-simplices. This is analogous to the condition in classical projective geometry
that a line must contain at least three points. However, there are degenerate
geometries which satisfy all the conditions to be a projective geometry except that the lines admit only two points. The analogous objects in the theory of buildings are called apartments. Apartments play such a constituent role in the theory of buildings that Tits conjectured the existence of a theory of projective geometry in which the degenerate geometries would have equal standing with the classical ones. This geometry would take place, he said, over a field of characteristic one. Using this analogy it was possible to describe some of the elementary properties of F1, but it was not possible to construct it.
A separate inspiration for F1 came from algebraic number theory
. Weil's proof of the Riemann hypothesis for curves over finite fields started with a curve C over a finite field k, took its product , and then examined its diagonal. If the integers were a curve over a field, the same proof would prove the Riemann hypothesis
. The integers Z are one dimensional
, which suggests that they may be a curve, but they are not an algebra over any field. One of the conjectured properties of F1 is that Z should be an F1-algebra. This would make it possible to construct the product , and it is hoped that the Riemann hypothesis for Z can be proved in the same way as the Riemann hypothesis for a curve over a finite field.
Another angle comes from Arakelov geometry, where Diophantine equations are studied using tools from complex geometry
. The theory involves complicated comparisons between finite fields and the complex numbers. Here the existence of F1 is useful for technical reasons.
In 1993, Yuri Manin gave a series of lectures on zeta functions where he proposed developing a theory of algebraic geometry over F1. He suggested that zeta functions of varieties over F1 would have very simple descriptions, and he proposed a relation between the K-theory
of F1 and the homotopy groups of spheres
. This inspired several people to attempt to construct F1. In 2000, Zhu proposed that F1 was the same as F2 except that the sum of one and one was one, not zero. Deitmar suggested that F1 should be found by forgetting the additive structure of a ring and focusing on the multiplication. Toën and Vaquié built on Hakim's theory of relative schemes and defined F1 using symmetric monoidal categories. Nikolai Durov
constructed F1 as a commutative algebraic monad
. Soulé constructed it using algebras over the complex numbers and functors from categories of certain rings. Borger used descent
to construct it from the finite fields and the integers.
Recently, Alain Connes
, Caterina Consani and Matilde Marcolli have connected F1 with noncommutative geometry
.
Sets are projective spaces : The number of elements of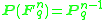
, the 
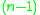-dimensional projective space
over the finite field
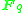, is the q-integer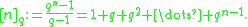
Taking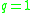
yields 
.
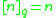The expansion of the q-integer into a sum of powers of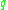
corresponds to the Schubert cell decomposition of projective space.
Permutations are flags : There are n! permutations of a set with n elements, and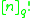
maximal flags in 
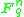, where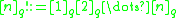
is the q-factorial. Indeed, a permutation of a set can be considered a filtered set, as a flag is a filtered vector space: for instance, the permutation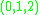
corresponds to the filtration 
.
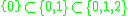Subsets are subspaces : The binomial coefficient
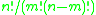gives the number of m-element subsets of an n-element set, and the q-binomial coefficient 
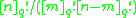gives the number of m-dimensional subspaces of an n-dimensional vector space over 
.
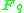The expansion of the q-binomial coefficient into a sum of powers of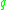
corresponds to the Schubert cell decomposition of the Grassmannian
.
s of the field with one element as the group of roots of unity, or more finely (with a geometric structure) as the group scheme of roots of unity. This is non-naturally isomorphic to the cyclic group
of order n, the isomorphism depending on choice of a primitive root of unity: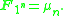
Thus a vector space of dimension d over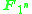
is a finite set of order dn on which the roots of unity act freely, together with a base point.
From this point of view the finite field
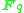is an algebra over 
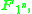of dimension 
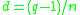for any n that is a factor of 
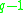(for example 
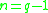or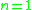 
). This corresponds to the fact that the group of units of a finite field 
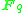(which are the 
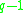non-zero elements) is a cyclic group of order 
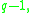on which any cyclic group of order dividing 
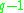acts freely (by raising to a power), and the zero element of the field is the base point.
Similarly, the real numbers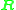
are an algebra over 
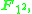of infinite dimension, as the real numbers contain ±1, but no other roots of unity, and the complex numbers 
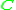are an algebra over 
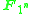for all n, again of infinite dimension, as the complex numbers have all roots of unity.
From this point of view, any phenomenon that only depends on a field having roots of unity can be seen as coming from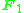
– for example, the discrete Fourier transform
(complex-valued) and the related number-theoretic transform (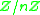
-valued).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the field with one element is a suggestive name for an object that should behave similarly to a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun. The name "field with one element" and the notation F1 are only suggestive, as there is no field with one element in classical abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
. Instead, F1 refers to the idea that there should be a way to replace sets and operations, the traditional building blocks for abstract algebra, with other, more flexible objects. While there is still no field with a single element in these theories, there is a field-like object whose characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
is one. This object is denoted F1.
F1 cannot be a field because all fields must contain two distinct elements, the additive identity
Additive identity
In mathematics the additive identity of a set which is equipped with the operation of addition is an element which, when added to any element x in the set, yields x...
zero and the multiplicative identity one. Even if this restriction is dropped, a ring with one element must be the trivial ring, which does not behave like a finite field. Instead, most proposed theories of F1 replace abstract algebra entirely. Mathematical objects such as vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s can be carried over into these new theories by mimicking their abstract properties. This allows the development of commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
on new foundations. One of the defining features of theories of F1 is that these new foundations allow more objects than classical abstract algebra, one of which behaves like a field of characteristic one.
The possibility of studying the mathematics of F1 was originally suggested in 1956 by Jacques Tits
Jacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
, published in , on the basis of an analogy between symmetries in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
and the combinatorics of simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
es. F1 has been connected to noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
and to a possible proof of the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. Many theories of F1 have been proposed, but it is not clear which, if any, of them give F1 all the desired properties.
History
In 1957, Jacques Tits introduced the theory of buildings, which relate algebraic groupAlgebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s to abstract simplicial complex
Abstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
es. One of the assumptions is a non-triviality condition: If the building is an n-dimensional abstract simplicial complex, and if , then every k-simplex of the building must be contained in at least three n-simplices. This is analogous to the condition in classical projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
that a line must contain at least three points. However, there are degenerate
Degeneracy (mathematics)
In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
geometries which satisfy all the conditions to be a projective geometry except that the lines admit only two points. The analogous objects in the theory of buildings are called apartments. Apartments play such a constituent role in the theory of buildings that Tits conjectured the existence of a theory of projective geometry in which the degenerate geometries would have equal standing with the classical ones. This geometry would take place, he said, over a field of characteristic one. Using this analogy it was possible to describe some of the elementary properties of F1, but it was not possible to construct it.
A separate inspiration for F1 came from algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
. Weil's proof of the Riemann hypothesis for curves over finite fields started with a curve C over a finite field k, took its product , and then examined its diagonal. If the integers were a curve over a field, the same proof would prove the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
. The integers Z are one dimensional
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
, which suggests that they may be a curve, but they are not an algebra over any field. One of the conjectured properties of F1 is that Z should be an F1-algebra. This would make it possible to construct the product , and it is hoped that the Riemann hypothesis for Z can be proved in the same way as the Riemann hypothesis for a curve over a finite field.
Another angle comes from Arakelov geometry, where Diophantine equations are studied using tools from complex geometry
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
. The theory involves complicated comparisons between finite fields and the complex numbers. Here the existence of F1 is useful for technical reasons.
In 1993, Yuri Manin gave a series of lectures on zeta functions where he proposed developing a theory of algebraic geometry over F1. He suggested that zeta functions of varieties over F1 would have very simple descriptions, and he proposed a relation between the K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
of F1 and the homotopy groups of spheres
Homotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
. This inspired several people to attempt to construct F1. In 2000, Zhu proposed that F1 was the same as F2 except that the sum of one and one was one, not zero. Deitmar suggested that F1 should be found by forgetting the additive structure of a ring and focusing on the multiplication. Toën and Vaquié built on Hakim's theory of relative schemes and defined F1 using symmetric monoidal categories. Nikolai Durov
Nikolai Durov
Nikolai Durov is a Russian mathematician and programmer. He is one of the founders of Vkontakte.ru web site.- Early life and education :...
constructed F1 as a commutative algebraic monad
Monad (category theory)
In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
. Soulé constructed it using algebras over the complex numbers and functors from categories of certain rings. Borger used descent
Descent (category theory)
In mathematics, the idea of descent has come to stand for a very general idea, extending the intuitive idea of 'gluing' in topology. Since the topologists' glue is actually the use of equivalence relations on topological spaces, the theory starts with some ideas on identification.A sophisticated...
to construct it from the finite fields and the integers.
Recently, Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
, Caterina Consani and Matilde Marcolli have connected F1 with noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
.
Properties
F1 is believed to have the following properties.- Finite sets are both affine spaceAffine spaceIn mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
s and projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s over F1. - Pointed setPointed setIn mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
s are vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over F1. - The finite fields Fq are quantum deformationsQuantum groupIn mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
of F1, where q is the deformation. - Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
s are simple algebraic groups over F1:- Given a Dynkin diagram for a simple algebraic group, its Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
is the simple algebraic group over F1. is a curve over F1.
- Given a Dynkin diagram for a simple algebraic group, its Weyl group
- Groups are Hopf algebraHopf algebraIn mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
s over F1. More generally, anything defined purely in terms of diagrams of algebraic objects should have an F1-analog in the category of sets. - Group actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s on sets are projective representations of G over F1, and in this way, G is the group Hopf algebraGroup Hopf algebraIn mathematics, the group Hopf algebra of a given group is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.-Definition:...
F1[G]. - Varieties over F1 are toric varieties, and all toric varieties determine F1-varieties.
- The zeta function of PN over F1 should be ζ(s) = s(s - 1)···(s - N).
- The mth K-group of F1 should be the mth stable homotopy group of the sphere spectrumSphere spectrumIn stable homotopy theory, a branch of mathematics, the sphere spectrum S is the smallest nontrivial spectrum. It is the suspension spectrum of S0, i.e., a set of two points. Explicitly, the nth space in the sphere spectrum is the n-dimensional sphere Sn, and the structure maps from the suspension...
.
Computations
Various structures on a set are analogous to structures on a projective space, and can be computed in the same way:Sets are projective spaces : The number of elements of
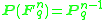, the 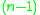-dimensional projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
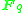, is the q-integer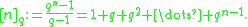Taking
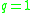yields 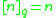.The expansion of the q-integer into a sum of powers of
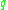corresponds to the Schubert cell decomposition of projective space.Permutations are flags : There are n! permutations of a set with n elements, and
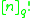maximal flags in 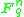, where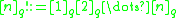is the q-factorial. Indeed, a permutation of a set can be considered a filtered set, as a flag is a filtered vector space: for instance, the permutation
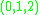corresponds to the filtration 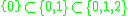.Subsets are subspaces : The binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
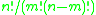gives the number of m-element subsets of an n-element set, and the q-binomial coefficient 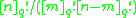gives the number of m-dimensional subspaces of an n-dimensional vector space over 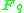.The expansion of the q-binomial coefficient into a sum of powers of
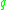corresponds to the Schubert cell decomposition of the GrassmannianGrassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
.
Field extensions
One may define field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s of the field with one element as the group of roots of unity, or more finely (with a geometric structure) as the group scheme of roots of unity. This is non-naturally isomorphic to the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order n, the isomorphism depending on choice of a primitive root of unity:
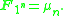
Thus a vector space of dimension d over
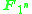is a finite set of order dn on which the roots of unity act freely, together with a base point.From this point of view the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
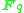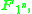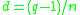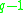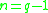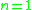is an algebra over of dimension for any n that is a factor of (for example or ). This corresponds to the fact that the group of units of a finite field 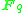(which are the 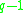non-zero elements) is a cyclic group of order 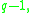on which any cyclic group of order dividing 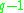acts freely (by raising to a power), and the zero element of the field is the base point.Similarly, the real numbers
are an algebra over of infinite dimension, as the real numbers contain ±1, but no other roots of unity, and the complex numbers 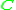are an algebra over 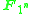for all n, again of infinite dimension, as the complex numbers have all roots of unity.From this point of view, any phenomenon that only depends on a field having roots of unity can be seen as coming from
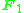– for example, the discrete Fourier transformDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(complex-valued) and the related number-theoretic transform (
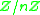-valued).External links
- John Baez's This Week's Finds in Mathematical Physics: Week 259
- The Field With One Element at the n-category cafe
- The Field With One Element at Secret Blogging Seminar
- Looking for Fun and The Fun folklore, Lieven le Bruyn.
- Fun Mathematics, Lieven le Bruyn, Koen Thas.
- Conference at IHES on algebraic geometry over
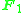
- Vanderbilt conference on Noncommutative Geometry and Geometry over the Field with One Element (Schedule)
- NCG and F_un, by Alain ConnesAlain ConnesAlain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and K. Consani: summary of talks and slides