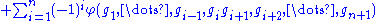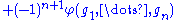Group cohomology
Encyclopedia
In abstract algebra
, homological algebra
, algebraic topology
and algebraic number theory
, as well as in applications to group theory
proper, group cohomology is a way to study groups
using a sequence of functor
s H n. The study of fixed points of groups acting on modules
and quotient module
s is a motivation, but the cohomology can be defined using various constructions. There is a dual theory, group homology, and a generalization to non-abelian coefficients.
These algebraic ideas are closely related to topological ideas. Thus, the group cohomology of a group G can be thought of as, and is motivated by, the singular cohomology of a suitable space having G as its fundamental group
, namely the corresponding Eilenberg-MacLane space
. Thus, the group cohomology of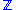
can be thought of as the singular cohomology of the circle 
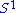, and similarly for 
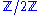and 
.
A great deal is known about the cohomology of groups, including interpretations of low dimensional cohomology, functorality, and how to change groups. The subject of group cohomology began in the 1920s, matured in the late 1940s, and continues as an area of active research today.
is that a group
G should be studied via its group representation
s. A slight generalization of those representations are the G-modules
: a G-module is an abelian group
M together with a group action
of G on M, with every element of G acting as an endomorphism
of M. In the sequel we will write G multiplicatively and M additively.
Given such a G-module M, it is natural to consider the subgroup of G-invariant elements:
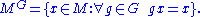
Now, if N is a submodule of M (i.e. a subgroup of M mapped to itself by the action of G), it isn't in general true that the invariants in M/N are found as the quotient of the invariants in M by N: being invariant 'up to something in N ' is broader. The first group cohomology H1(G,N) precisely measures the difference. The group cohomology functors Hn in general measure the extent to which taking invariants doesn't respect exact sequence
s. This is expressed by a long exact sequence.
(the morphisms are group homomorphisms f with the property f(gx) = g(f(x)) for all g in G and x in M). This category of G-modules is an abelian category with enough injectives (since it is isomorphic to the category of all modules
over the group ring
ℤ[G]).
Sending each module M to the group of invariants MG yields a functor
from this category to the category
of abelian groups. This functor is left exact but not necessarily right exact. We may therefore form its right derived functor
s; their values are abelian groups and they are denoted by Hn(G,M), "the n-th cohomology group of G with coefficients in M". H0(G,M) is identified with MG.
is a short exact sequence of G-modules, then a long exact sequence
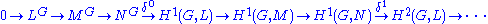
is induced. The maps δn are called the "connecting homomorphisms" and can be obtained from the snake lemma
.
s from Gn to M. This is an abelian group; its elements are called the (inhomogeneous) n-cochains. The coboundary homomorphisms
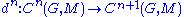
are defined as
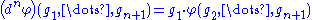
The crucial thing to check here is
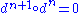
thus we have a cochain complex and we can compute cohomology. For n ≥ 0, define the group of n-cocycles as:
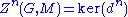
and the group of n-coboundaries as
and
ℤ[G], which allows one to define group cohomology via Ext functor
s:
where M is a ℤ[G]-module.
Here ℤ is treated as the trivial G-module: every element of G acts as the identity. These Ext groups can also be computed via a projective resolution of ℤ, the advantage being that such a resolution only depends on G and not on M. We recall the definition of Ext more explicitly for this context. Let F be a projective ℤ[G]-resolution (e.g. a free ℤ[G]-resolution) of the trivial ℤ[G]-module ℤ:
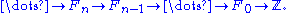
e.g., one may always take the resolution of group rings,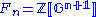
, with morphisms
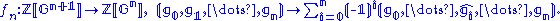
Recall that for ℤ[G]-modules N and M, HomG(N, M) is an abelian group
consisting of ℤ[G]-homomorphisms from N to M.
Since HomG(–, M) is a contravariant functor and reverses the arrows, applying HomG(–, M) to F termwise produces a cochain complex HomG(F, M):
The cohomology groups H*(G,M) of G with coefficients in M are defined as the cohomology of the above cochain complex:
for n ≥ 0.
M, set DM to be the submodule generated
by elements of the form g·m-m, g∈G, m∈M. Assigning to M its so-called coinvariants, the quotient
,
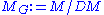is a right exact functor. Its left derived functors are by definition the group homology
.
Note that the superscript/subscript convention for cohomology/homology agrees with the convention for group invariants/coinvariants, while which is denoted "co-" switches:
The covariant functor which assigns MG to M is isomorphic to the functor which sends M to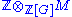
, where 
is endowed with the trivial G-action. Hence one also gets an expression for group homology in terms of the Tor functor
s,
Recall that the tensor product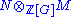
is defined whenever N is a right ℤ[G]-module and M is a left ℤ[G]-module. If N is a left ℤ[G]-module, we turn it into a right ℤ[G]-module by setting a g = g− 1 a for every g ∈ G and every a ∈ N. This convention allows to define the tensor product 
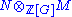in the case where both M and N are left ℤ[G]-modules.
Specifically, the homology groups Hn(G, M) can be computed as follows. Start with a projective resolution F of the trivial ℤ[G]-module ℤ, as in the previous section. Apply the covariant functor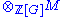
to F termwise to get a chain complex
:
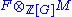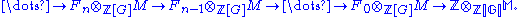
Then Hn(G, M) are the homology groups of this chain complex,
for n ≥ 0.
Group homology and cohomology can be treated uniformly for some groups, especially finite group
s, in terms of complete resolutions and the Tate cohomology group
s.
The zeroth cohomology of G with coefficients in A is
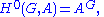
which is a subgroup of A.
The first cohomology of G with coefficents in A is defined as above using 1-cocycles and 1-coboundaries. However, it is generally not a group when A is non-abelian. It instead has the structure of a pointed set
– exactly the same situation arises in the 0th homotopy group
,
which for a general topological space is not a group but a pointed set. Note that a group is in particular a pointed set, with the identity element as distinguished point.
Using explicit calculations, one still obtains a truncated long exact sequence in cohomology. Specifically, let
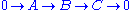
be a short exact sequence of G-groups, then there is an exact sequence of pointed sets
BG. (If G has no topology about which we care, then we assign the discrete topology to G. In this case, BG is an Eilenberg-MacLane space
K(G,1), whose fundamental group
is G and whose higher homotopy group
s vanish). The n-th cohomology of BG, with coefficients in M (in the topological sense), is the same as the group cohomology of G with coefficients in M. This will involve a local coefficient system unless M is a trivial G-module. The connection holds because the total space EG is contractible, so its chain complex forms a projective resolution of M. These connections are explained in , Chapter II.
When M is a ring with trivial G-action, we inherit good properties which are familiar from the topological context: in particular, there is a cup product
under which
is a graded module, and a Künneth formula applies.
If, furthermore, M=k is a field, then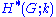
is a graded k-algebra. In this case, the Künneth formula yields
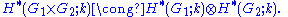
For example, let G be the group with two elements, under the discrete topology. The real projective space
is a classifying space for G. Let k=F2, the field
of two elements. Then
a polynomial k-algebra on a single generator, since this is the cellular cohomology ring of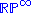
.
Hence, as a second example, if G is an elementary abelian 2-group
of rank r, and k=F2, then the Künneth formula gives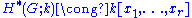
,
a polynomial k-algebra generated by r classes in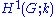
.
, then we have a naturally induced morphism Hn(G,M) → Hn(H,M) (where in the latter, M is treated as an H-module via f).
Given a morphism of G-modules M→N, one gets a morphism of cohomology groups in the Hn(G,M) → Hn(G,N).
satisfying 
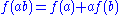for all 
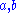in G, modulo the so-called principal crossed homomorphisms, i.e. maps 
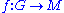given by 
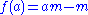for some fixed 
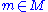. This follows from the definition of cochains above.
If the action of G on M is trivial, then the above boils down to
, the group of group homomorphism
s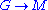
.
s of G by M in which the induced action of G on M by inner automorphism
s agrees with the given action.
the category of representations of a finite group is semi-simple over any field of characteristic zero (or more generally, any field whose characteristic does not divide the order of the group), hence, viewing group cohomology as a derived functor in this abelian category, one obtains that it is zero. The other argument is that over a field of characteristic zero, the group algebra of a finite group is a direct sum of matrix algebras (possibly over division algebras which are extensions of the original field), while a matrix algebra is Morita equivalent to its base field and hence has trivial cohomology.
in 1897; this was recast into Noether
's equations in Galois theory
(an appearance of cocycles for H1). The idea of factor sets for the extension problem for groups (connected with H2) arose in the work of Hölder
(1893), in Issai Schur
's 1904 study of projective representations, in Schreier
's 1926 treatment, and in Richard Brauer
's 1928 study of simple algebras and the Brauer group
. A fuller discussion of this history may be found in .
In 1941, while studying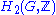
(which plays a special role in groups), Hopf
discovered what is now called Hopf's integral homology formula , which is identical to Schur's formula for the Schur multiplier
of a finite, finitely presented group:
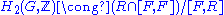, where 
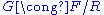and F is a free group.
Hopf's result led to the independent discovery of group cohomology by several groups in 1943-45: Eilenberg
and Mac Lane
in the USA ; Hopf and Eckmann
in Switzerland; and Freudenthal
in the Netherlands . The situation was chaotic because communication between these countries was difficult during World War II.
From a topological point of view, the homology and cohomology of G was first defined as the homology and cohomology of a model for the topological classifying space
BG as discussed in #Connections with topological cohomology theories above. In practice, this meant using topology to produce the chain complexes used in formal algebraic definitions. From a module-theoretic point of view this was integrated into the Cartan
-Eilenberg
theory of Homological algebra
in the early 1950s.
The application in algebraic number theory
to class field theory
provided theorems valid for general Galois extension
s (not just abelian extension
s). The cohomological part of class field theory was axiomatized as the theory of class formation
s. In turn, this led to the notion of Galois cohomology
and étale cohomology
(which builds on it) . Some refinements in the theory post-1960 have been made, such as continuous cocycles and Tate
's redefinition
, but the basic outlines remain the same. This is a large field, and now basic in the theories of algebraic group
s.
The analogous theory for Lie algebra
s, called Lie algebra cohomology
, was first developed in the late 1940s, by Chevalley-Eilenberg, and Koszul
. It is formally similar, using the corresponding definition of invariant for the action of a Lie algebra. It is much applied in representation theory
, and is closely connected with the BRST quantization
of theoretical physics
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, as well as in applications to group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
proper, group cohomology is a way to study groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
using a sequence of functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s H n. The study of fixed points of groups acting on modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and quotient module
Quotient module
In abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
s is a motivation, but the cohomology can be defined using various constructions. There is a dual theory, group homology, and a generalization to non-abelian coefficients.
These algebraic ideas are closely related to topological ideas. Thus, the group cohomology of a group G can be thought of as, and is motivated by, the singular cohomology of a suitable space having G as its fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, namely the corresponding Eilenberg-MacLane space
Eilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
. Thus, the group cohomology of
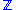can be thought of as the singular cohomology of the circle 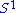, and similarly for 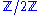and .A great deal is known about the cohomology of groups, including interpretations of low dimensional cohomology, functorality, and how to change groups. The subject of group cohomology began in the 1920s, matured in the late 1940s, and continues as an area of active research today.
Motivation
A general paradigm in group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
is that a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G should be studied via its group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s. A slight generalization of those representations are the G-modules
G-module
In mathematics, given a group G, a G-module is an abelian group M on which G acts compatibly with the abelian group structure on M. This widely applicable notion generalizes that of a representation of G...
: a G-module is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
M together with a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on M, with every element of G acting as an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of M. In the sequel we will write G multiplicatively and M additively.
Given such a G-module M, it is natural to consider the subgroup of G-invariant elements:
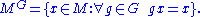
Now, if N is a submodule of M (i.e. a subgroup of M mapped to itself by the action of G), it isn't in general true that the invariants in M/N are found as the quotient of the invariants in M by N: being invariant 'up to something in N ' is broader. The first group cohomology H1(G,N) precisely measures the difference. The group cohomology functors Hn in general measure the extent to which taking invariants doesn't respect exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
s. This is expressed by a long exact sequence.
Formal constructions
In this article, G is a finite group. The collection of all G-modules is a categoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
(the morphisms are group homomorphisms f with the property f(gx) = g(f(x)) for all g in G and x in M). This category of G-modules is an abelian category with enough injectives (since it is isomorphic to the category of all modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
ℤ[G]).
Sending each module M to the group of invariants MG yields a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from this category to the category
of abelian groups. This functor is left exact but not necessarily right exact. We may therefore form its right derived functorDerived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s; their values are abelian groups and they are denoted by Hn(G,M), "the n-th cohomology group of G with coefficients in M". H0(G,M) is identified with MG.
Long exact sequence of cohomology
In practice, one often computes the cohomology groups using the following fact: ifis a short exact sequence of G-modules, then a long exact sequence
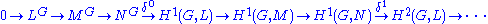
is induced. The maps δn are called the "connecting homomorphisms" and can be obtained from the snake lemma
Snake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
.
Cochain complexes
Rather than using the machinery of derived functors, the cohomology groups can also be defined more concretely, as follows. For n ≥ 0, let Cn(G, M) be the group of all functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s from Gn to M. This is an abelian group; its elements are called the (inhomogeneous) n-cochains. The coboundary homomorphisms
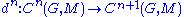
are defined as
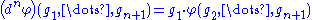
The crucial thing to check here is
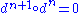
thus we have a cochain complex and we can compute cohomology. For n ≥ 0, define the group of n-cocycles as:
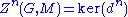
and the group of n-coboundaries as
and
The functors Ext
n and formal definition of group cohomology Yet another approach is to treat G-modules as modules over the group ringGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
ℤ[G], which allows one to define group cohomology via Ext functor
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
s:
where M is a ℤ[G]-module.
Here ℤ is treated as the trivial G-module: every element of G acts as the identity. These Ext groups can also be computed via a projective resolution of ℤ, the advantage being that such a resolution only depends on G and not on M. We recall the definition of Ext more explicitly for this context. Let F be a projective ℤ[G]-resolution (e.g. a free ℤ[G]-resolution) of the trivial ℤ[G]-module ℤ:
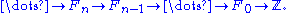
e.g., one may always take the resolution of group rings,
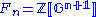, with morphisms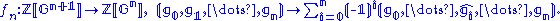Recall that for ℤ[G]-modules N and M, HomG(N, M) is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
consisting of ℤ[G]-homomorphisms from N to M.
Since HomG(–, M) is a contravariant functor and reverses the arrows, applying HomG(–, M) to F termwise produces a cochain complex HomG(F, M):
The cohomology groups H*(G,M) of G with coefficients in M are defined as the cohomology of the above cochain complex:
for n ≥ 0.
Group homology
Dually to the construction of group cohomology there is the following definition of group homology: given a G-moduleG-module
In mathematics, given a group G, a G-module is an abelian group M on which G acts compatibly with the abelian group structure on M. This widely applicable notion generalizes that of a representation of G...
M, set DM to be the submodule generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by elements of the form g·m-m, g∈G, m∈M. Assigning to M its so-called coinvariants, the quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
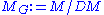,is a right exact functor. Its left derived functors are by definition the group homology
.Note that the superscript/subscript convention for cohomology/homology agrees with the convention for group invariants/coinvariants, while which is denoted "co-" switches:
- superscripts correspond to cohomology
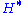and invariants 
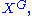while - subscripts correspond to homology
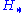and coinvariants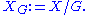 
The covariant functor which assigns MG to M is isomorphic to the functor which sends M to
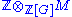, where is endowed with the trivial G-action. Hence one also gets an expression for group homology in terms of the Tor functorTor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
s,
Recall that the tensor product
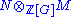is defined whenever N is a right ℤ[G]-module and M is a left ℤ[G]-module. If N is a left ℤ[G]-module, we turn it into a right ℤ[G]-module by setting a g = g− 1 a for every g ∈ G and every a ∈ N. This convention allows to define the tensor product 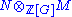in the case where both M and N are left ℤ[G]-modules.Specifically, the homology groups Hn(G, M) can be computed as follows. Start with a projective resolution F of the trivial ℤ[G]-module ℤ, as in the previous section. Apply the covariant functor
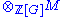to F termwise to get a chain complexChain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
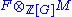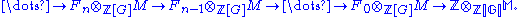
:Then Hn(G, M) are the homology groups of this chain complex,
for n ≥ 0.Group homology and cohomology can be treated uniformly for some groups, especially finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, in terms of complete resolutions and the Tate cohomology group
Tate cohomology group
In mathematics, Tate cohomology groups are a slightly modified form of the usual cohomology groups of a finite group that combine homology and cohomology groups into one sequence...
s.
Connecting homomorphisms
For a short exact sequence 0 → L → M → N → 0, the connecting homomorphisms δn : Hn(G, N) → Hn+1(G, L) can be described in terms of inhomogeneous cochains as follows. If c is an element of Hn(G, N) represented by an n-cocycle φ : Gn → N, then δn(c) is represented by dn(ψ), where ψ is an n-cochain Gn → M "lifting" φ (i.e. such that φ is the composition of ψ with the surjective map M → N).Non-abelian group cohomology
Using the G-invariants and the 1-cochains, one can construct the zeroth and first group cohomology for a group G with coefficients in a non-abelian group. Specifically, a G-group is a (not necessarily abelian) group A together with an action by G.The zeroth cohomology of G with coefficients in A is
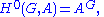
which is a subgroup of A.
The first cohomology of G with coefficents in A is defined as above using 1-cocycles and 1-coboundaries. However, it is generally not a group when A is non-abelian. It instead has the structure of a pointed set
Pointed set
In mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
– exactly the same situation arises in the 0th homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
,
which for a general topological space is not a group but a pointed set. Note that a group is in particular a pointed set, with the identity element as distinguished point.Using explicit calculations, one still obtains a truncated long exact sequence in cohomology. Specifically, let
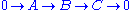
be a short exact sequence of G-groups, then there is an exact sequence of pointed sets
Connections with topological cohomology theories
Group cohomology can be related to topological cohomology theories: to the topological group G there is an associated classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BG. (If G has no topology about which we care, then we assign the discrete topology to G. In this case, BG is an Eilenberg-MacLane space
Eilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
K(G,1), whose fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
is G and whose higher homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s vanish). The n-th cohomology of BG, with coefficients in M (in the topological sense), is the same as the group cohomology of G with coefficients in M. This will involve a local coefficient system unless M is a trivial G-module. The connection holds because the total space EG is contractible, so its chain complex forms a projective resolution of M. These connections are explained in , Chapter II.
When M is a ring with trivial G-action, we inherit good properties which are familiar from the topological context: in particular, there is a cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
under which
is a graded module, and a Künneth formula applies.
If, furthermore, M=k is a field, then
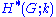is a graded k-algebra. In this case, the Künneth formula yields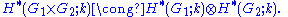For example, let G be the group with two elements, under the discrete topology. The real projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
is a classifying space for G. Let k=F2, the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of two elements. Then
a polynomial k-algebra on a single generator, since this is the cellular cohomology ring of
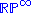.Hence, as a second example, if G is an elementary abelian 2-group
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
of rank r, and k=F2, then the Künneth formula gives
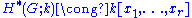,a polynomial k-algebra generated by r classes in
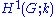.Functoriality
Group cohomology depends contravariantly on the group G, in the following sense: if f : H → G is a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
, then we have a naturally induced morphism Hn(G,M) → Hn(H,M) (where in the latter, M is treated as an H-module via f).
Given a morphism of G-modules M→N, one gets a morphism of cohomology groups in the Hn(G,M) → Hn(G,N).
H1
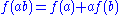The first cohomology group is the quotient of the so-called crossed homomorphisms, i.e. maps (of sets) satisfying for all 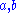in G, modulo the so-called principal crossed homomorphisms, i.e. maps 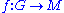given by 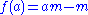for some fixed 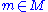. This follows from the definition of cochains above.If the action of G on M is trivial, then the above boils down to
, the group of group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s
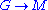.H2
If M is a trivial G-module (i.e. the action of G on M is trivial), the second cohomology group H2(G,M) is in one-to-one correspondence with the set of central extensions of G by M (up to a natural equivalence relation). More generally, if the action of G on M is nontrivial, H2(G,M) classifies the isomorphism classes of all extensionGroup extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
s of G by M in which the induced action of G on M by inner automorphism
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
s agrees with the given action.
Change of group
The Hochschild-Serre spectral sequence relates the cohomology of a normal subgroup N of G and the quotient G/N to the cohomology of the group G (for (pro-)finite groups G).Cohomology of finite groups is torsion
The cohomology groups of finite groups are all torsion. Indeed, by Maschke's theoremMaschke's theorem
In mathematics, Maschke's theorem, named after Heinrich Maschke, is a theorem in group representation theory that concerns the decomposition of representations of a finite group into irreducible pieces...
the category of representations of a finite group is semi-simple over any field of characteristic zero (or more generally, any field whose characteristic does not divide the order of the group), hence, viewing group cohomology as a derived functor in this abelian category, one obtains that it is zero. The other argument is that over a field of characteristic zero, the group algebra of a finite group is a direct sum of matrix algebras (possibly over division algebras which are extensions of the original field), while a matrix algebra is Morita equivalent to its base field and hence has trivial cohomology.
History and relation to other fields
The low dimensional cohomology of a group was classically studied in other guises, long before the notion of group cohomology was formulated in 1943-45. The first theorem of the subject can be identified as Hilbert's Theorem 90Hilbert's Theorem 90
In abstract algebra, Hilbert's Theorem 90 refers to an important result on cyclic extensions of fields that leads to Kummer theory...
in 1897; this was recast into Noether
Emmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
's equations in Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
(an appearance of cocycles for H1). The idea of factor sets for the extension problem for groups (connected with H2) arose in the work of Hölder
Otto Hölder
Otto Ludwig Hölder was a German mathematician born in Stuttgart.Hölder first studied at the Polytechnikum and then in 1877 went to Berlin where he was a student of Leopold Kronecker, Karl Weierstraß, and Ernst Kummer.He is famous for many things including: Hölder's inequality, the Jordan–Hölder...
(1893), in Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
's 1904 study of projective representations, in Schreier
Otto Schreier
Otto Schreier was an Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups. He studied mathematics at the University of Vienna and obtained his doctorate in 1923, under the supervision of Philipp Furtwängler...
's 1926 treatment, and in Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
's 1928 study of simple algebras and the Brauer group
Brauer group
In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is...
. A fuller discussion of this history may be found in .
In 1941, while studying
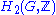(which plays a special role in groups), HopfHeinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
discovered what is now called Hopf's integral homology formula , which is identical to Schur's formula for the Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
of a finite, finitely presented group:
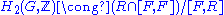, where 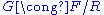and F is a free group.Hopf's result led to the independent discovery of group cohomology by several groups in 1943-45: Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
and Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
in the USA ; Hopf and Eckmann
Beno Eckmann
Beno Eckmann was a Swiss mathematician who was a student of Heinz Hopf.Born in Bern, Eckmann received his master's degree from Eidgenössische Technische Hochschule Zürich in 1931. Later he studied there under Heinz Hopf, obtaining his Ph.D. in 1941...
in Switzerland; and Freudenthal
Hans Freudenthal
Hans Freudenthal was a Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education....
in the Netherlands . The situation was chaotic because communication between these countries was difficult during World War II.
From a topological point of view, the homology and cohomology of G was first defined as the homology and cohomology of a model for the topological classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
BG as discussed in #Connections with topological cohomology theories above. In practice, this meant using topology to produce the chain complexes used in formal algebraic definitions. From a module-theoretic point of view this was integrated into the Cartan
Henri Cartan
Henri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
-Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
theory of Homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
in the early 1950s.
The application in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
to class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
provided theorems valid for general Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
s (not just abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
s). The cohomological part of class field theory was axiomatized as the theory of class formation
Class formation
In mathematics, a class formation is a structure used to organize the various Galois groups and modules that appear in class field theory. They were invented by Emil Artin and John Tate.-Definitions:...
s. In turn, this led to the notion of Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
and étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
(which builds on it) . Some refinements in the theory post-1960 have been made, such as continuous cocycles and Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
's redefinition
Tate cohomology group
In mathematics, Tate cohomology groups are a slightly modified form of the usual cohomology groups of a finite group that combine homology and cohomology groups into one sequence...
, but the basic outlines remain the same. This is a large field, and now basic in the theories of algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s.
The analogous theory for Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, called Lie algebra cohomology
Lie algebra cohomology
In mathematics, Lie algebra cohomology is a cohomology theory for Lie algebras. It was defined by in order to give an algebraic construction of the cohomology of the underlying topological spaces of compact Lie groups...
, was first developed in the late 1940s, by Chevalley-Eilenberg, and Koszul
Jean-Louis Koszul
Jean-Louis Koszul is a mathematician best known for studying geometry and discovering the Koszul complex.He was educated at the Lycée Fustel-de-Coulanges in Strasbourg before studying at the Faculty of Science in Strasbourg and the Faculty of Science in Paris...
. It is formally similar, using the corresponding definition of invariant for the action of a Lie algebra. It is much applied in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, and is closely connected with the BRST quantization
BRST quantization
In theoretical physics, BRST quantization is a relatively rigorous mathematical approach to quantizing a field theory with a gauge symmetry...
of theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
.