
Length function
Encyclopedia
In mathematical field of geometric group theory
, a length function is a function that assigns a number to each element of a group.
G is a function satisfying:
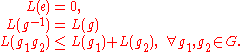
Compare with the axioms for a metric
and a filtered algebra
.
by generators and relations, the length of an element is the length of the shortest word expressing it.
Coxeter group
s (including the symmetric group
) have combinatorial important length functions, using the simple reflections as generators (thus each simple reflection has length 1).
A longest element of a Coxeter group
is both important and unique up to conjugation (up to different choice of simple reflections).
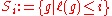 do not form subgroups in general.
do not form subgroups in general.
However, the group algebra
of a group with a length functions forms a filtered algebra
: the axiom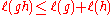 corresponds to the filtration axiom.
corresponds to the filtration axiom.
----
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, a length function is a function that assigns a number to each element of a group.
Definition
A length function L : G → R+ on a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is a function satisfying:
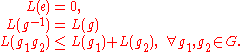
Compare with the axioms for a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
and a filtered algebra
Filtered algebra
In mathematics, a filtered algebra is a generalization of the notion of a graded algebra. Examples appear in many branches of mathematics, especially in homological algebra and representation theory....
.
Word metric
An important example of a length is the word metric: given a presentation of a groupPresentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
by generators and relations, the length of an element is the length of the shortest word expressing it.
Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s (including the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
) have combinatorial important length functions, using the simple reflections as generators (thus each simple reflection has length 1).
A longest element of a Coxeter group
Longest element of a Coxeter group
In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
is both important and unique up to conjugation (up to different choice of simple reflections).
Properties
A group with a length function does not form a filtered group, meaning that the sublevel sets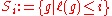 do not form subgroups in general.
do not form subgroups in general.However, the group algebra
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of a group with a length functions forms a filtered algebra
Filtered algebra
In mathematics, a filtered algebra is a generalization of the notion of a graded algebra. Examples appear in many branches of mathematics, especially in homological algebra and representation theory....
: the axiom
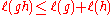 corresponds to the filtration axiom.
corresponds to the filtration axiom.----

