Hasse diagram
Encyclopedia
In order theory
, a branch of mathematics
, a Hasse diagram (icon; German
: /ˈhasə/) is a type of mathematical diagram
used to represent a finite partially ordered set
, in the form of a drawing
of its transitive reduction
. Concretely, for a partially ordered set (S, ≤) one represents each element of S as a vertex
in the plane and draws a line segment
or curve that goes upward from x to y whenever y covers
x (that is, whenever x < y and there is no z such that x < z < y).
These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.
Hasse diagrams are named after Helmut Hasse
(1898–1979); according to , they are so-called because of the effective use Hasse made of them. However, Hasse was not the first to use these diagrams; they appear, e.g., in . Although Hasse diagrams were originally devised as a technique for making drawings of partially ordered sets by hand, they have more recently been created automatically using graph drawing
techniques.
The phrase "Hasse diagram" may also refer to the transitive reduction as an abstract directed acyclic graph
, independently of any drawing of that graph, but this usage is eschewed here.

, it turns out to be rather difficult to draw "good" diagrams. The reason is that there will in general be many possible ways to draw a Hasse diagram for a given poset. The simple technique of just starting with the minimal elements of an order and then adding greater elements incrementally often produces quite poor results: symmetries and internal structure of the order are easily lost.
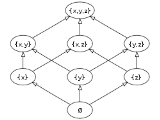
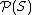 of the set S = {a, b, c, d}, i.e. the set of all subset
of the set S = {a, b, c, d}, i.e. the set of all subset
s of S, ordered via subset inclusion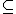 . Below are three different Hasse diagrams for this partial order (Note that each subset S’ has a node labeled with a 1-0 encoding of whether each of the four elements is ('1') or isn't ('0') in S’.):
. Below are three different Hasse diagrams for this partial order (Note that each subset S’ has a node labeled with a 1-0 encoding of whether each of the four elements is ('1') or isn't ('0') in S’.):
The leftmost diagram makes clear that the powerset is a graded poset
. The middle diagram has the same graded structure, but by making some edges longer than others, it emphasizes a construction of the powerset as a union of two three-dimensional cubes: the vertices in the lower (left) cube represent subsets that do not contain some particular element (say d) of S, while those in the upper (right) cube represent the subsets that do contain d. The rightmost diagram shows some of the internal symmetry of the structure.
, ordered by the refinement relation. The diagram on the left emphasizes that the elements 0...4 form a sublattice. The whole lattice is not simply a doubled sublattice like in the hypercube example above. The second diagram is reflectionally symmetrical. The edges in the middle would all be vertical lines, but to make them discriminable, they are drawn slightly curved. The third diagram emphasizes the rank structure
of the lattice. All elements with the same rank are in the same level of the Hasse diagram, but most of the symmetry is lost.
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Hasse diagram (icon; German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
: /ˈhasə/) is a type of mathematical diagram
Mathematical diagram
Mathematical diagrams are diagrams in the field of mathematics, and diagrams using mathematics such as charts and graphs, that are mainly designed to convey mathematical relationships, for example, comparisons over time.- Argand diagram :...
used to represent a finite partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
, in the form of a drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
of its transitive reduction
Transitive reduction
In mathematics, a transitive reduction of a binary relation R on a set X is a minimal relation R' on X such that the transitive closure of R' is the same as the transitive closure of R. If the transitive closure of R is antisymmetric and finite, then R' is unique...
. Concretely, for a partially ordered set (S, ≤) one represents each element of S as a vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
in the plane and draws a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
or curve that goes upward from x to y whenever y covers
Covering relation
In mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are immediate neighbours...
x (that is, whenever x < y and there is no z such that x < z < y).
These curves may cross each other but must not touch any vertices other than their endpoints. Such a diagram, with labeled vertices, uniquely determines its partial order.
Hasse diagrams are named after Helmut Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
(1898–1979); according to , they are so-called because of the effective use Hasse made of them. However, Hasse was not the first to use these diagrams; they appear, e.g., in . Although Hasse diagrams were originally devised as a technique for making drawings of partially ordered sets by hand, they have more recently been created automatically using graph drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
techniques.
The phrase "Hasse diagram" may also refer to the transitive reduction as an abstract directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
, independently of any drawing of that graph, but this usage is eschewed here.
Examples
- The power set of { x, y, z } partially ordered by inclusion, has the Hasse diagram:

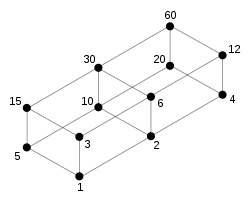
- The set A = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 } of all divisors of 60, partially ordered by divisibility, has the Hasse diagram:

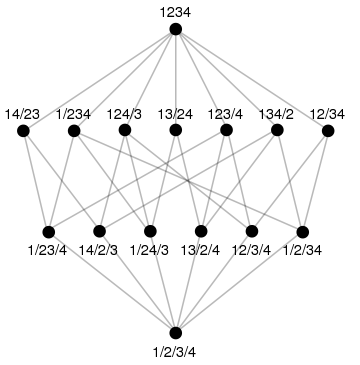
- The set of all 15 partitionsPartition of a setIn mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of the set { 1, 2, 3, 4 }, partially ordered by refinement (i.e. a finer partition is "less than" a coarser partition), has the Hasse diagram:

A "good" Hasse diagram
Although Hasse diagrams are simple as well as intuitive tools for dealing with finite posetsPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
, it turns out to be rather difficult to draw "good" diagrams. The reason is that there will in general be many possible ways to draw a Hasse diagram for a given poset. The simple technique of just starting with the minimal elements of an order and then adding greater elements incrementally often produces quite poor results: symmetries and internal structure of the order are easily lost.
Subsets
The following example demonstrates the issue. Consider the powerset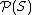 of the set S = {a, b, c, d}, i.e. the set of all subset
of the set S = {a, b, c, d}, i.e. the set of all subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of S, ordered via subset inclusion
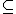 . Below are three different Hasse diagrams for this partial order (Note that each subset S’ has a node labeled with a 1-0 encoding of whether each of the four elements is ('1') or isn't ('0') in S’.):
. Below are three different Hasse diagrams for this partial order (Note that each subset S’ has a node labeled with a 1-0 encoding of whether each of the four elements is ('1') or isn't ('0') in S’.):The leftmost diagram makes clear that the powerset is a graded poset
Graded poset
In mathematics, in the branch of combinatorics, a graded poset, sometimes called a ranked poset , is a partially ordered set P equipped with a rank function ρ from P to N compatible with the ordering such that whenever y covers x, then...
. The middle diagram has the same graded structure, but by making some edges longer than others, it emphasizes a construction of the powerset as a union of two three-dimensional cubes: the vertices in the lower (left) cube represent subsets that do not contain some particular element (say d) of S, while those in the upper (right) cube represent the subsets that do contain d. The rightmost diagram shows some of the internal symmetry of the structure.
Partitions
The following Hasse diagrams also show a 4 element set's partitionsPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
, ordered by the refinement relation. The diagram on the left emphasizes that the elements 0...4 form a sublattice. The whole lattice is not simply a doubled sublattice like in the hypercube example above. The second diagram is reflectionally symmetrical. The edges in the middle would all be vertical lines, but to make them discriminable, they are drawn slightly curved. The third diagram emphasizes the rank structure
Graded poset
In mathematics, in the branch of combinatorics, a graded poset, sometimes called a ranked poset , is a partially ordered set P equipped with a rank function ρ from P to N compatible with the ordering such that whenever y covers x, then...
of the lattice. All elements with the same rank are in the same level of the Hasse diagram, but most of the symmetry is lost.
Upward planarity
If a partial order can be drawn as a Hasse diagram in which no two edges cross, its covering graph is said to be upward planar. A number of results on upward planarity and on crossing-free Hasse diagram construction are known:- If the partial order to be drawn is a latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, then it can be drawn without crossings if and only if it has order dimensionOrder dimensionIn mathematics, the dimension of a partially ordered set is the smallest number of total orders the intersection of which gives rise to the partial order....
at most two. In this case, a non-crossing drawing may be found by deriving Cartesian coordinates for the elements from their positions in the two linear orders realizing the order dimension, and then rotating the drawing counterclockwise by a 45-degree angle. - If the partial order has at most one minimal element, or it has at most one maximal elementMaximal elementIn mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
, then it may be tested in linear time whether it has a non-crossing Hasse diagram. - It is NP-complete to determine whether a partial order with multiple sources and sinks can be drawn as a crossing-free Hasse diagram. However, finding a crossing-free Hasse diagram is fixed-parameter tractable when parametrized by the number of articulation points and triconnected components of the transitive reduction of the partial order.
- If the y-coordinates of the elements of a partial order are specified, then a crossing-free Hasse diagram respecting those coordinate assignments can be found in linear time, if such a diagram exists. In particular, if the input poset is a graded posetGraded posetIn mathematics, in the branch of combinatorics, a graded poset, sometimes called a ranked poset , is a partially ordered set P equipped with a rank function ρ from P to N compatible with the ordering such that whenever y covers x, then...
, it is possible to determine in linear time whether there is a crossing-free Hasse diagram in which the height of each vertex is proportional to its rank.

