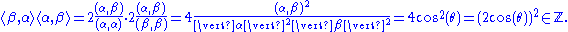
Root system
Encyclopedia
In mathematics
, a root system is a configuration of vector
s in a Euclidean space
satisfying certain geometrical properties. The concept is fundamental in the theory of Lie group
s and Lie algebra
s. Since Lie groups (and some analogues such as algebraic group
s) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory
). Finally, root systems are important for their own sake, as in graph theory
in the study of eigenvalues.
vector space
, with the standard Euclidean inner product
denoted by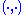
. A root system in V is a finite set Φ of non-zero vectors (called roots) that satisfy the following properties:
Some authors only include conditions 1–3 in the definition of a root system. In this context, a root system that also satisfies the integrality condition is known as a crystallographic root system. Other authors omit condition 2; then they call root systems satisfying condition 2 reduced. In this article, all root systems are assumed to be reduced and crystallographic.
In view of property 3, the integrality condition is equivalent to stating that β and its reflection σα(β) differ by an integer multiple of α. Note that the operator
defined by property 4 is not an inner product. It is not necessarily symmetric and is linear only in the first argument.
The cosine of the angle between two roots is constrained to be a half-integral multiple of a square root of an integer:
Since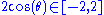
, the only possible values are 
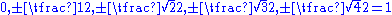, corresponding to angles of 90°, 60° or 120°, 45° or 135°, 30° or 150°, and 0 or 180°. Condition 2 says that no scalar multiples of α other than 1 and -1 can be roots, so 0 or 180°, which would correspond to 2α or -2α are out.
The rank of a root system Φ is the dimension of V.
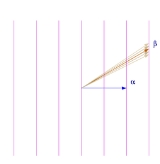
Two root systems may be combined by regarding the Euclidean spaces they span as mutually orthogonal subspaces of a common Euclidean space. A root system which does not arise from such a combination, such as the systems A2, B2, and G2 pictured below, is said to be irreducible.
Two irreducible root systems (E1, Φ1) and (E2, Φ2) are considered to be the same if there is an invertible linear transformation E1 → E2 which sends Φ1 to Φ2.
The group
of isometries
of V generated by reflections through hyperplanes associated to the roots of Φ is called the Weyl group
of Φ. As it acts faithfully
on the finite set Φ, the Weyl group is always finite.
The of a root system Φ is the Z-submodule of V generated by Φ. It is a lattice
in V.
>
There is only one root system of rank 1, consisting of two nonzero vectors
. This root system is called 
.
In rank 2 there are four possibilities, corresponding to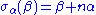
, where 
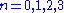. Note that the lattice generated by a root system is not unique: 
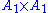and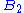 
generate a square lattice
while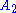
and 
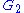generate a hexagonal lattice
, only two of the five possible types of lattices in two dimensions.
Whenever Φ is a root system in V, and W is a subspace
of V spanned by Ψ = Φ ∩ W, then Ψ is a root system in W. Thus, the exhaustive list of four root systems of rank 2 shows the geometric possibilities for any two roots chosen from a root system of arbitrary rank. In particular, two such roots must meet at an angle of 0, 30, 45, 60, 90, 120, 135, 150, or 180 degrees.
of Φ such that
If a set of positive roots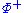
is chosen, elements of –
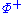are called negative roots.
An element of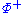
is called a simple root if it cannot be written as the sum of two elements of 
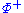. The set 
of simple roots is a basis of 
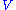with the property that every vector in 
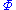is a linear combination of elements of 
with all coefficients non-negative, or all coefficients non-positive. For each choice of positive roots, the corresponding set of simple roots is the unique set of roots such that the positive roots are exactly those that can be expressed as a combination of them with non-negative coefficients, and such that these combinations are unique.
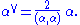
The set of coroots also forms a root system ΦV in V, called the dual root system (or sometimes inverse root system).
By definition, αV V = α, so that Φ is the dual root system of ΦV. The lattice in V spanned by ΦV is called the coroot lattice. Both Φ and ΦV have the same Weyl group W and, for s in W,
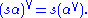
If Δ is a set of simple roots for Φ, then ΔV is a set of simple roots for ΦV.
to certain graphs
, the Dynkin diagrams named after Eugene Dynkin
. The classification of these graphs is a simple matter of combinatorics
, and induces a classification of irreducible root systems.
Given a root system, select a set Δ of simple roots as in the preceding section. The vertices of the associated Dynkin diagram correspond to vectors in Δ. An edge is drawn between each non-orthogonal pair of vectors; it is an undirected single edge if they make an angle of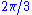
radians, a directed double edge if they make an angle of 
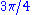radians, and a directed triple edge if they make an angle of 
radians. The term "directed edge" means that double and triple edges are marked with an angle sign pointing toward the shorter vector.
Although a given root system has more than one possible set of simple roots, the Weyl group
acts transitively on such choices. Consequently, the Dynkin diagram is independent of the choice of simple roots; it is determined by the root system itself. Conversely, given two root systems with the same Dynkin diagram, one can match up roots, starting with the roots in the base, and show that the systems are in fact the same.
Thus the problem of classifying root systems reduces to the problem of classifying possible Dynkin diagrams. Root systems are irreducible if and only if their Dynkin diagrams are connected. Dynkin diagrams encode the inner product on E in terms of the basis Δ, and the condition that this inner product must be positive definite turns out to be all that is needed to get the desired classification.
The actual connected diagrams are as follows. The subscripts indicate the number of vertices in the diagram (and hence the rank of the corresponding irreducible root system).
Irreducible root systems are named according to their corresponding connected Dynkin diagrams. There are four infinite families (An, Bn, Cn, and Dn, called the classical root systems) and five exceptional cases (the exceptional root systems). The subscript indicates the rank of the root system.
In an irreducible root system there can be at most two values for the length (α, α)1/2, corresponding to short and long roots. If all roots have the same length they are taken to be long by definition and the root system is said to be simply laced; this occurs in the cases A, D and E. Any two roots of the same length lie in the same orbit of the Weyl group. In the non-simply laced cases B, C, G and F, the root lattice is spanned by the short roots and the long roots span a sublattice, invariant under the Weyl group, equal to r2/2 times the coroot lattice, where r is the length of a long root.
In the table to the right, |Φ < | denotes the number of short roots, I denotes the index in the root lattice of the sublattice generated by long roots, D denotes the determinant of the Cartan matrix
, and |W| denotes the order of the Weyl group
.
Let V be the subspace of Rn+1 for which the coordinates sum to 0, and let Φ be the set of vectors in V of length √2 and which are integer vectors, i.e. have integer coordinates in Rn+1. Such a vector must have all but two coordinates equal to 0, one coordinate equal to 1, and one equal to –1, so there are n2 + n roots in all. One choice of simple roots expressed in the standard basis
is: αi = ei – ei+1, for 1 ≤ i ≤ n.
The reflection
σi through the hyperplane
perpendicular to αi is the same as permutation
of the adjacent i-th and (i + 1)-th coordinates. Such
transpositions generate the full permutation group
.
For adjacent simple roots,
σi(αi+1) = αi+1 + αi = σi+1(αi) = αi + αi+1, that is, reflection is equivalent to adding a multiple of 1; but
reflection of a simple root perpendicular to a nonadjacent simple root leaves it unchanged, differing by a multiple of 0.
Let V = Rn, and let Φ consist of all integer vectors in V of length 1 or √2. The total number of roots is 2n2. One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i ≤ n – 1 (the above choice of simple roots for An-1), and the shorter root αn = en.
The reflection σn through the hyperplane perpendicular to the short root αn is of course simply negation of the nth coordinate.
For the long simple root αn-1, σn-1(αn) = αn + αn-1, but for reflection perpendicular to the short root, σn(αn-1) = αn-1 + 2αn, a difference by a multiple of 2 instead of 1.
B1 is isomorphic to A1 via scaling by √2, and is therefore not a distinct root system.
Let V = Rn, and let Φ consist of all integer vectors in V of length √2 together with all vectors of the form 2λ, where λ is an integer vector of length 1. The total number of roots is 2n2. One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i ≤ n – 1 (the above choice of simple roots for An-1), and the longer root αn = 2en.
The reflection σn(αn-1) = αn-1 + αn, but σn-1(αn) = αn + 2αn-1.
C2 is isomorphic to B2 via scaling by √2 and a 45 degree rotation, and is therefore not a distinct root system.
Root system B3, C3, and A3=D3 as points within a cube
and octahedron
Let V = Rn, and let Φ consist of all integer vectors in V of length √2. The total number of roots is 2n(n – 1). One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i < n (the above choice of simple roots for An-1) plus αn = en + en-1.
Reflection through the hyperplane perpendicular to αn is the same as transposing and negating the adjacent n-th and (n – 1)-th coordinates. Any simple root and its reflection perpendicular to another simple root differ by a multiple of 0 or 1 of the second root, not by any greater multiple.
D3 reduces to A3, and is therefore not a distinct root system.
D4 has additional symmetry called triality
.
The root system has 240 roots.
The set just listed is the set of vectors of length √2 in the E8 lattice
Γ8, which is the set of points in R8 such that:
Thus,
An alternative description of the E8 lattice which is sometimes convenient is as the set Γ'8 of all points in R8 such that
The lattices Γ8 and Γ'8 are isomorphic; one may pass from one to the other by changing the signs of any odd number of coordinates. The lattice Γ8 is sometimes called the even coordinate system for E8 while the lattice Γ'8 is called the odd coordinate system.
One choice of simple roots for E8 in the even coordinate system is
(the above choice of simple roots for D7) along with
One choice of simple roots for E8 in the odd coordinate system is
(the above choice of simple roots for A7) along with
(Using β3 would give an isomorphic result. Using β1,7 or β2,6 would simply give A8 or D8. As for β4, its coordinates sum to 0, and the same is true for α1...7, so they span only the 7-dimensional subspace for which the coordinates sum to 0; in fact –2β4 has coordinates (1,2,3,4,3,2,1) in the basis (αi).)
Deleting α1 and then α2 gives sets of simple roots for E7 and E6.
Since perpendicularity to α1 means that the first two coordinates are equal, E7 is then the subset of E8 where the first two coordinates are equal, and similarly E6 is the subset of E8 where the first three coordinates are equal. This facilitates explicit definitions of E7 and E6 as:
For F4, let V = R4, and let Φ denote the set of vectors α of length 1 or √2 such that the coordinates of 2α are all integers and are either all even or all odd. There are 48 roots in this system. One choice of simple roots is: the choice of simple roots given above for B4, plus α4 = –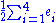
.
The root system G2 has 12 roots, which form the vertices of a hexagram. See the picture above.
One choice of simple roots is: (α1,
β = α2 – α1) where
αi = ei – ei+1 for i = 1, 2 is the above choice of simple roots for A2.
In each case, the roots are non-zero weight
s of the adjoint representation.
In the case of a simply connected simple compact Lie group G with maximal torus
T, the root lattice can naturally be identified with Hom(T, T) and the coroot lattice with Hom(T, T); see .
For connections between the exceptional root systems and their Lie groups and Lie algebras see E8
, E7, E6, F4, and G2.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a root system is a configuration of vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
satisfying certain geometrical properties. The concept is fundamental in the theory of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s. Since Lie groups (and some analogues such as algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
). Finally, root systems are important for their own sake, as in graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
in the study of eigenvalues.
Definitions
Let V be a finite-dimensional EuclideanEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, with the standard Euclidean inner product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
denoted by
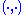. A root system in V is a finite set Φ of non-zero vectors (called roots) that satisfy the following properties:- The roots spanLinear spanIn the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
V. - The only scalar multiples of a root α ∈ Φ that belong to Φ are α itself and –α.
- For every root α ∈ Φ, the set Φ is closed under reflectionReflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
through the hyperplaneHyperplaneA hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
perpendicular to α. That is, for any two roots α and β, the set Φ contains the reflection of β, - (Integrality condition) If α and β are roots in Φ, then the projection of β onto the line through α is a half-integral multiple of α. That is,
Some authors only include conditions 1–3 in the definition of a root system. In this context, a root system that also satisfies the integrality condition is known as a crystallographic root system. Other authors omit condition 2; then they call root systems satisfying condition 2 reduced. In this article, all root systems are assumed to be reduced and crystallographic.
In view of property 3, the integrality condition is equivalent to stating that β and its reflection σα(β) differ by an integer multiple of α. Note that the operator
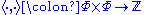
defined by property 4 is not an inner product. It is not necessarily symmetric and is linear only in the first argument.
The cosine of the angle between two roots is constrained to be a half-integral multiple of a square root of an integer:
Since
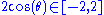, the only possible values are 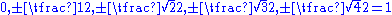, corresponding to angles of 90°, 60° or 120°, 45° or 135°, 30° or 150°, and 0 or 180°. Condition 2 says that no scalar multiples of α other than 1 and -1 can be roots, so 0 or 180°, which would correspond to 2α or -2α are out.The rank of a root system Φ is the dimension of V.
Two root systems may be combined by regarding the Euclidean spaces they span as mutually orthogonal subspaces of a common Euclidean space. A root system which does not arise from such a combination, such as the systems A2, B2, and G2 pictured below, is said to be irreducible.
Two irreducible root systems (E1, Φ1) and (E2, Φ2) are considered to be the same if there is an invertible linear transformation E1 → E2 which sends Φ1 to Φ2.
The group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of V generated by reflections through hyperplanes associated to the roots of Φ is called the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of Φ. As it acts faithfully
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the finite set Φ, the Weyl group is always finite.
The of a root system Φ is the Z-submodule of V generated by Φ. It is a lattice
Lattice (discrete subgroup)
In Lie theory and related areas of mathematics, a lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space has finite invariant measure...
in V.
Rank-1 and rank-2 examples
Root system  |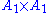
Root system  |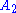
Root system  |
Root system  |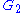
There is only one root system of rank 1, consisting of two nonzero vectors
. This root system is called .In rank 2 there are four possibilities, corresponding to
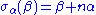, where 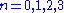. Note that the lattice generated by a root system is not unique: 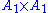and 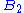generate a square latticeSquare lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
while
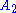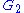and generate a hexagonal latticeHexagonal lattice
The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
, only two of the five possible types of lattices in two dimensions.
Whenever Φ is a root system in V, and W is a subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
of V spanned by Ψ = Φ ∩ W, then Ψ is a root system in W. Thus, the exhaustive list of four root systems of rank 2 shows the geometric possibilities for any two roots chosen from a root system of arbitrary rank. In particular, two such roots must meet at an angle of 0, 30, 45, 60, 90, 120, 135, 150, or 180 degrees.
Positive roots and simple roots
Given a root system Φ we can always choose (in many ways) a set of positive roots. This is a subset of Φ such that
- For each root
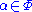exactly one of the roots 
, –
is contained in 
. - For any two distinct
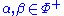such that 
is a root,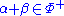 
.
If a set of positive roots
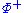is chosen, elements of – 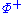are called negative roots.An element of
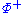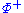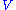is called a simple root if it cannot be written as the sum of two elements of . The set of simple roots is a basis of with the property that every vector in 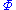is a linear combination of elements of with all coefficients non-negative, or all coefficients non-positive. For each choice of positive roots, the corresponding set of simple roots is the unique set of roots such that the positive roots are exactly those that can be expressed as a combination of them with non-negative coefficients, and such that these combinations are unique.Dual root system and coroots
If Φ is a root system in V, the coroot αV of a root α is defined by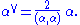The set of coroots also forms a root system ΦV in V, called the dual root system (or sometimes inverse root system).
By definition, αV V = α, so that Φ is the dual root system of ΦV. The lattice in V spanned by ΦV is called the coroot lattice. Both Φ and ΦV have the same Weyl group W and, for s in W,
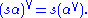
If Δ is a set of simple roots for Φ, then ΔV is a set of simple roots for ΦV.
Classification of root systems by Dynkin diagrams
Irreducible root systems correspondBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
to certain graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, the Dynkin diagrams named after Eugene Dynkin
Eugene Dynkin
Eugene Borisovich Dynkin is a Soviet and American mathematician. He has made contributions to the fields of probability and algebra, especially semisimple Lie groups, Lie algebras, and Markov processes...
. The classification of these graphs is a simple matter of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, and induces a classification of irreducible root systems.
Given a root system, select a set Δ of simple roots as in the preceding section. The vertices of the associated Dynkin diagram correspond to vectors in Δ. An edge is drawn between each non-orthogonal pair of vectors; it is an undirected single edge if they make an angle of
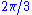radians, a directed double edge if they make an angle of 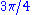radians, and a directed triple edge if they make an angle of radians. The term "directed edge" means that double and triple edges are marked with an angle sign pointing toward the shorter vector.Although a given root system has more than one possible set of simple roots, the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
acts transitively on such choices. Consequently, the Dynkin diagram is independent of the choice of simple roots; it is determined by the root system itself. Conversely, given two root systems with the same Dynkin diagram, one can match up roots, starting with the roots in the base, and show that the systems are in fact the same.
Thus the problem of classifying root systems reduces to the problem of classifying possible Dynkin diagrams. Root systems are irreducible if and only if their Dynkin diagrams are connected. Dynkin diagrams encode the inner product on E in terms of the basis Δ, and the condition that this inner product must be positive definite turns out to be all that is needed to get the desired classification.
The actual connected diagrams are as follows. The subscripts indicate the number of vertices in the diagram (and hence the rank of the corresponding irreducible root system).
Properties of the irreducible root systems
 |
I | D | |||
|---|---|---|---|---|---|
| An (n ≥ 1) | n(n + 1) | n + 1 | (n + 1)! | ||
| Bn (n ≥ 2) | 2n2 | 2n | 2 | 2 | 2n n! |
| Cn (n ≥ 3) | 2n2 | 2n(n − 1) | 2 | 2 | 2n n! |
| Dn (n ≥ 4) | 2n(n − 1) | 4 | 2n − 1 n! | ||
| E6 | 72 | 3 | 51840 | ||
| E7 | 126 | 2 | 2903040 | ||
| E8 E8 (mathematics) In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8... |
240 | 1 | 696729600 | ||
| F4 | 48 | 24 | 4 | 1 | 1152 |
| G2 | 12 | 6 | 3 | 1 | 12 |
Irreducible root systems are named according to their corresponding connected Dynkin diagrams. There are four infinite families (An, Bn, Cn, and Dn, called the classical root systems) and five exceptional cases (the exceptional root systems). The subscript indicates the rank of the root system.
In an irreducible root system there can be at most two values for the length (α, α)1/2, corresponding to short and long roots. If all roots have the same length they are taken to be long by definition and the root system is said to be simply laced; this occurs in the cases A, D and E. Any two roots of the same length lie in the same orbit of the Weyl group. In the non-simply laced cases B, C, G and F, the root lattice is spanned by the short roots and the long roots span a sublattice, invariant under the Weyl group, equal to r2/2 times the coroot lattice, where r is the length of a long root.
In the table to the right, |Φ < | denotes the number of short roots, I denotes the index in the root lattice of the sublattice generated by long roots, D denotes the determinant of the Cartan matrix
Cartan matrix
In mathematics, the term Cartan matrix has three meanings. All of these are named after the French mathematician Élie Cartan. In fact, Cartan matrices in the context of Lie algebras were first investigated by Wilhelm Killing, whereas the Killing form is due to Cartan.- Lie algebras :A generalized...
, and |W| denotes the order of the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
.
An
| 1 | −1 | 0 | 0 |
| 0 | 1 | −1 | 0 |
| 0 | 0 | 1 | −1 |
Let V be the subspace of Rn+1 for which the coordinates sum to 0, and let Φ be the set of vectors in V of length √2 and which are integer vectors, i.e. have integer coordinates in Rn+1. Such a vector must have all but two coordinates equal to 0, one coordinate equal to 1, and one equal to –1, so there are n2 + n roots in all. One choice of simple roots expressed in the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
is: αi = ei – ei+1, for 1 ≤ i ≤ n.
The reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
σi through the hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
perpendicular to αi is the same as permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the adjacent i-th and (i + 1)-th coordinates. Such
transpositions generate the full permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
.
For adjacent simple roots,
σi(αi+1) = αi+1 + αi = σi+1(αi) = αi + αi+1, that is, reflection is equivalent to adding a multiple of 1; but
reflection of a simple root perpendicular to a nonadjacent simple root leaves it unchanged, differing by a multiple of 0.
Bn
| 1 | |||
| 0 | 0 | ||
| 0 | 1 | ||
| 0 | |||
| 0 | 0 | 1 | |
| 0 | 0 | 0 | 1 |
Let V = Rn, and let Φ consist of all integer vectors in V of length 1 or √2. The total number of roots is 2n2. One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i ≤ n – 1 (the above choice of simple roots for An-1), and the shorter root αn = en.
The reflection σn through the hyperplane perpendicular to the short root αn is of course simply negation of the nth coordinate.
For the long simple root αn-1, σn-1(αn) = αn + αn-1, but for reflection perpendicular to the short root, σn(αn-1) = αn-1 + 2αn, a difference by a multiple of 2 instead of 1.
B1 is isomorphic to A1 via scaling by √2, and is therefore not a distinct root system.
Cn
| 1 | |||
| 0 | 0 | ||
| 0 | 1 | ||
| 0 | |||
| 0 | 0 | 1 | |
| 0 | 0 | 0 | 2 |
Let V = Rn, and let Φ consist of all integer vectors in V of length √2 together with all vectors of the form 2λ, where λ is an integer vector of length 1. The total number of roots is 2n2. One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i ≤ n – 1 (the above choice of simple roots for An-1), and the longer root αn = 2en.
The reflection σn(αn-1) = αn-1 + αn, but σn-1(αn) = αn + 2αn-1.
C2 is isomorphic to B2 via scaling by √2 and a 45 degree rotation, and is therefore not a distinct root system.
Root system B3, C3, and A3=D3 as points within a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
and octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
Dn
| 1 | |||
| 0 | 0 | ||
| 0 | 1 | ||
| 0 | |||
| 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 |
Let V = Rn, and let Φ consist of all integer vectors in V of length √2. The total number of roots is 2n(n – 1). One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i < n (the above choice of simple roots for An-1) plus αn = en + en-1.
Reflection through the hyperplane perpendicular to αn is the same as transposing and negating the adjacent n-th and (n – 1)-th coordinates. Any simple root and its reflection perpendicular to another simple root differ by a multiple of 0 or 1 of the second root, not by any greater multiple.
D3 reduces to A3, and is therefore not a distinct root system.
D4 has additional symmetry called triality
Triality
In mathematics, triality is a relationship between three vector spaces, analogous to the duality relation between dual vector spaces. Most commonly, it describes those special features of the Dynkin diagram D4 and the associated Lie group Spin, the double cover of 8-dimensional rotation group SO,...
.
E8, E7, E6
72 vertices of 122 represent the root vectors of E6 (Orange nodes are doubled in this E6 Coxeter plane projection) |
 126 vertices of 231 represent the root vectors of E7 |
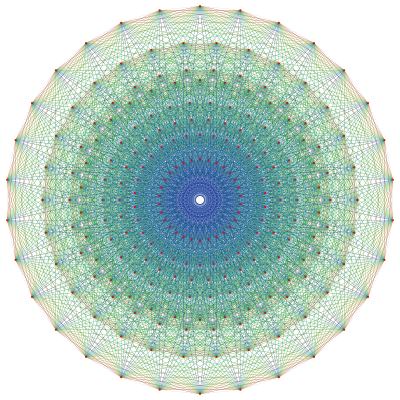 240 vertices of 421 represent the root vectors of E8 E8 (mathematics) In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8... |
- The E8 root system is any set of vectors in R8 that is congruentCongruence (geometry)In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
to the following set:
- D8 ∪ { ½( ∑i=18 εiei) : εi = ±1, ε1•••ε8 = +1}.
The root system has 240 roots.
The set just listed is the set of vectors of length √2 in the E8 lattice
E8 lattice
In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
Γ8, which is the set of points in R8 such that:
- all the coordinates are integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s or all the coordinates are half-integerHalf-integerIn mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
s (a mixture of integers and half-integers is not allowed), and - the sum of the eight coordinates is an even integer.
Thus,
- E8 = {α ∈ Z8 ∪ (Z+½)8 : |α|2 = ∑αi2 = 2, ∑αi ∈ 2Z}.
- The root system E7 is the set of vectors in E8 that are perpendicular to a fixed root in E8. The root system E7 has 126 roots.
- The root system E6 is not the set of vectors in E7 that are perpendicular to a fixed root in E7, indeed, one obtains D6 that way. However, E6 is the subsystem of E8 perpendicular to two suitably chosen roots of E8. The root system E6 has 72 roots.
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 1 | |||||
| 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 1 | ||||
| 0 | 0 | 0 | |||||
| 0 | 0 | 0 | 0 | 1 | |||
| 0 | 0 | ||||||
| 0 | 0 | 0 | 0 | 0 | 1 | ||
| 0 | |||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| -½ | |||||||
An alternative description of the E8 lattice which is sometimes convenient is as the set Γ'8 of all points in R8 such that
- all the coordinates are integers and the sum of the coordinates is even, or
- all the coordinates are half-integers and the sum of the coordinates is odd.
The lattices Γ8 and Γ'8 are isomorphic; one may pass from one to the other by changing the signs of any odd number of coordinates. The lattice Γ8 is sometimes called the even coordinate system for E8 while the lattice Γ'8 is called the odd coordinate system.
One choice of simple roots for E8 in the even coordinate system is
- αi = ei – ei+1, for 1 ≤ i ≤ 6, and
- α7 = e7 + e6
(the above choice of simple roots for D7) along with
- α8 = β0 =
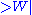= (-½,-½,-½,-½,-½,-½,-½,-½).
Simple roots in E8: odd coordinates 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 -½ ½ ½ ½
One choice of simple roots for E8 in the odd coordinate system is
- αi = ei – ei+1, for 1 ≤ i ≤ 7
(the above choice of simple roots for A7) along with
- α8 = β5, where
- βj =
.
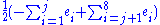(Using β3 would give an isomorphic result. Using β1,7 or β2,6 would simply give A8 or D8. As for β4, its coordinates sum to 0, and the same is true for α1...7, so they span only the 7-dimensional subspace for which the coordinates sum to 0; in fact –2β4 has coordinates (1,2,3,4,3,2,1) in the basis (αi).)
Deleting α1 and then α2 gives sets of simple roots for E7 and E6.
Since perpendicularity to α1 means that the first two coordinates are equal, E7 is then the subset of E8 where the first two coordinates are equal, and similarly E6 is the subset of E8 where the first three coordinates are equal. This facilitates explicit definitions of E7 and E6 as:
- E7 = {α ∈ Z7 ∪ (Z+½)7 : ∑αi2 + α12 = 2, ∑αi + α1 ∈ 2Z},
- E6 = {α ∈ Z6 ∪ (Z+½)6 : ∑αi2 + 2α12 = 2, ∑αi + 2α1 ∈ 2Z}
F4
| 1 | |||
| 0 | 0 | ||
| 0 | 1 | ||
| 0 | |||
| 0 | 0 | 1 | 0 |
| -½ | |||
For F4, let V = R4, and let Φ denote the set of vectors α of length 1 or √2 such that the coordinates of 2α are all integers and are either all even or all odd. There are 48 roots in this system. One choice of simple roots is: the choice of simple roots given above for B4, plus α4 = –
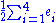.G2
| 1 | -1 | 0 |
| -1 | 2 | |
The root system G2 has 12 roots, which form the vertices of a hexagram. See the picture above.
One choice of simple roots is: (α1,
β = α2 – α1) where
αi = ei – ei+1 for i = 1, 2 is the above choice of simple roots for A2.
Root systems and Lie theory
Irreducible root systems classify a number of related objects in Lie theory, notably the- simple Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s (see the list of simple Lie groups), including the - simple complex Lie groupsSimple Lie groupIn group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
; - their associated simple complex Lie algebras; and
- simply connected complex Lie groups which are simple modulo centers.
In each case, the roots are non-zero weight
Weight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
s of the adjoint representation.
In the case of a simply connected simple compact Lie group G with maximal torus
Maximal torus
In the mathematical theory of compact Lie groups a special role is played by torus subgroups, in particular by the maximal torus subgroups.A torus in a Lie group G is a compact, connected, abelian Lie subgroup of G . A maximal torus is one which is maximal among such subgroups...
T, the root lattice can naturally be identified with Hom(T, T) and the coroot lattice with Hom(T, T); see .
For connections between the exceptional root systems and their Lie groups and Lie algebras see E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
, E7, E6, F4, and G2.
See also
- ADE classificationADE classificationIn mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
- Affine root systemAffine root systemIn mathematics, an affine root system is a root system of affine-linear functions on a Euclidean space. They are used in the classification of affine Lie algebras and superalgebras, and semisimple p-adic algebraic groups, and correspond to families of Macdonald polynomials. The reduced affine root...
- Coxeter–Dynkin diagram
- Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
- Coxeter matrix
- Dynkin diagram
- root datumRoot datumIn mathematics, the root datum of a connected split reductive algebraic group over a field is a generalization of a root system that determines the group up to isomorphism...
- Weyl groupWeyl groupIn mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
Further reading
- Dynkin, E. B. The structure of semi-simple algebras. Uspehi Matem. Nauk (N.S.) 2, (1947). no. 4(20), 59–127.