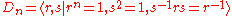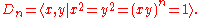Dihedral group
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a dihedral group is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of a regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
, including both rotations
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
and reflections
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
. Dihedral groups are among the simplest examples of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, and they play an important role in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
.
See also: Dihedral symmetry in three dimensions
Dihedral symmetry in three dimensions
This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
.
Notation
There are two competing notationsMathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
for the dihedral group associated to a polygon with n sides. In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
the group is denoted Dn, while in algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
the same group is denoted by D2n to indicate the number of elements.
In this article, Dn (and sometimes Dihn) refers to the symmetries of a regular polygon with n sides.
Elements
A regular polygon with n sides has 2n different symmetries: n rotational symmetriesRotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
and n reflection symmetries
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...
. The associated rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s and reflections
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
make up the dihedral group Dn. If n is odd each axis of symmetry connects the mid-point of one side to the opposite vertex. If n is even there are n/2 axes of symmetry connecting the mid-points of opposite sides and n/2 axes of symmetry connecting opposite vertices. In either case, there are n axes of symmetry altogether and 2n elements in the symmetry group. Reflecting in one axis of symmetry followed by reflecting in another axis of symmetry produces a rotation through twice the angle between the axes. The following picture shows the effect of the sixteen elements of D8 on a stop sign
Stop sign
A Stop sign is a traffic sign to notify drivers that they must stop before proceeding.-Specifications:The Vienna Convention on Road Signs and Signals proposed standard stop sign diameters of 0.6, 0.9 or 1.2 metres. UK and New Zealand stop signs are 750, 900 or 1200 mm, according to sign...
:
The first row shows the effect of the eight rotations, and the second row shows the effect of the eight reflections.
Group structure
As with any geometric object, the composition of two symmetries of a regular polygon is again a symmetry. This operation gives the symmetries of a polygon the algebraic structure of a finite groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
The following Cayley table
Cayley table
A Cayley table, after the 19th century British mathematician Arthur Cayley, describes the structure of a finite group by arranging all the possible products of all the group's elements in a square table reminiscent of an addition or multiplication table...
shows the effect of composition in the group D3 (the symmetries of an equilateral triangle). R0 denotes the identity; R1 and R2 denote counterclockwise rotations by 120 and 240 degrees; and S0, S1, and S2 denote reflections across the three lines shown in the picture to the right.
| R0 | R1 | R2 | S0 | S1 | S2 | |
|---|---|---|---|---|---|---|
| R0 | R0 | R1 | R2 | S0 | S1 | S2 |
| R1 | R1 | R2 | R0 | S1 | S2 | S0 |
| R2 | R2 | R0 | R1 | S2 | S0 | S1 |
| S0 | S0 | S2 | S1 | R0 | R2 | R1 |
| S1 | S1 | S0 | S2 | R1 | R0 | R2 |
| S2 | S2 | S1 | S0 | R2 | R1 | R0 |
For example, S2S1 = R1 because the reflection S1 followed by the reflection S2 results in a 120-degree rotation. (This is the normal backwards order for composition.) Note that the composition operation is not commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
.
In general, the group Dn has elements R0,...,Rn−1 and S0,...,Sn−1, with composition given by the following formulae:

In all cases, addition and subtraction of subscripts should be performed using modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
with modulus n.
Matrix representation
If we center the regular polygon at the origin, then elements of the dihedral group act as linear transformations of the planeCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
. This lets us represent elements of Dn as matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, with composition being matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
.
This is an example of a (2-dimensional) group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
.
For example, the elements of the group D4 can be represented by the following eight matrices:

In general, the matrices for elements of Dn have the following form:
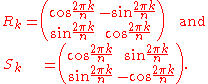
Rk is a rotation matrix, expressing a counterclockwise rotation through an angle of . Sk is a reflection across a line that makes an angle of with the x-axis.
Small dihedral groups
For n = 1 we have Dih1. This notation is rarely used except in the framework of the series, because it is equal to Z2. For n = 2 we have Dih2, the Klein four-groupKlein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
. Both are exceptional within the series:
- They are abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
; for all other values of n the group Dihn is not abelian. - They are not subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn, corresponding to the fact that 2n > n ! for these n.
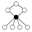
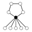
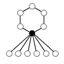
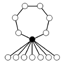
The cycle graphs of dihedral groups consist of an n-element cycle and n 2-element cycles. The dark vertex in the cycle graphs below of various dihedral groups stand for the identity element, and the other vertices are the other elements of the group. A cycle consists of successive powers of either of the elements connected to the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
.
 |
 |
 |
 |
 |
 |
 |
|---|---|---|---|---|---|---|
| Dih1 | Dih2 | Dih3 | Dih4 | Dih5 | Dih6 | Dih7 |
The dihedral group as symmetry group in 2D and rotation group in 3D
An example of abstract group Dihn, and a common way to visualize it, is the group Dn of Euclidean plane isometriesEuclidean plane isometry
In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length...
which keep the origin fixed. These groups form one of the two series of discrete point groups in two dimensions
Point groups in two dimensions
In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O, including O itself...
. Dn consists of n rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s of multiples of 360°/n about the origin, and reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s across n lines through the origin, making angles of multiples of 180°/n with each other. This is the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
with n sides (for n ≥ 3; this extends to the cases n = 1 and n = 2 where we have a plane with respectively a point offset from the "center" of the "1-gon" and a "2-gon" or line segment).
Dihedral group Dn is generated
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by a rotation r of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
n and a reflection s of order 2 such that
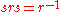
In geometric terms: in the mirror a rotation looks like an inverse rotation.
In terms of complex numbers: multiplication by
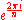 and complex conjugation.
and complex conjugation.In matrix form, by setting
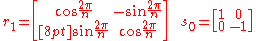
and defining
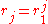 and
and 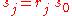 for
for  we can write the product rules for Dn as
we can write the product rules for Dn as

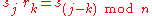
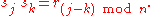
(Compare coordinate rotations and reflections
Coordinate rotations and reflections
In geometry, 2D coordinate rotations and reflections are two kinds of Euclidean plane isometries which are related to one another.A rotation in the plane can be formed by composing a pair of reflections. First reflect a point P to its image P′ on the other side of line L1...
.)
The dihedral group D2 is generated by the rotation r of 180 degrees, and the reflection s across the x-axis. The elements of D2 can then be represented as {e, r, s, rs}, where e is the identity or null transformation and rs is the reflection across the y-axis.
D2 is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
.
For n>2 the operations of rotation and reflection in general do not commute and Dn is not abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
; for example, in D4, a rotation of 90 degrees followed by a reflection yields a different result from a reflection followed by a rotation of 90 degrees.
Thus, beyond their obvious application to problems of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
in the plane, these groups are among the simplest examples of non-abelian groups, and as such arise frequently as easy counterexamples to theorems which are restricted to abelian groups.
The 2n elements of Dn can be written as e, r, r2, ..., rn−1, s, r s, r2 s, ..., rn−1 s. The first n listed elements are rotations and the remaining n elements are axis-reflections (all of which have order 2). The product of two rotations or two reflections is a rotation; the product of a rotation and a reflection is a reflection.
So far, we have considered Dn to be a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of O(2)
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, i.e. the group of rotations (about the origin) and reflections (across axes through the origin) of the plane. However, notation Dn is also used for a subgroup of SO(3) which is also of abstract group type Dihn: the proper symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a regular polygon embedded in three-dimensional space (if n ≥ 3). Such a figure may be considered as a degenerate regular solid with its face counted twice. Therefore it is also called a dihedron (Greek: solid with two faces), which explains the name dihedral group (in analogy to tetrahedral, octahedral and icosahedral group, referring to the proper symmetry groups of a regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, and icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
respectively).
Equivalent definitions
Further equivalent definitions of Dihn are:- The automorphism group of the graphGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
consisting only of a cycle with n vertices (if n ≥ 3). - The group with presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
-
- or
- From the second presentation follows that Dihn belongs to the class of Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s.- The semidirect productSemidirect productIn mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s Zn and Z2, with Z2 acting on Zn by inversion (thus, Dihn always has a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
isomorphic to the group Zn
- The semidirect product
 is isomorphic to Dihn if
is isomorphic to Dihn if 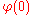 is the identity and
is the identity and  is inversion.
is inversion.Properties
If we consider Dihn (n ≥ 3) as the symmetry group of a regular n-gon and number the polygon's vertices, we see that Dihn is a subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn via this permutation representation.
The properties of the dihedral groups Dihn with n ≥ 3 depend on whether n is even or odd. For example, the center of Dihn consists only of the identity if n is odd, but if n is even the center has two elements, namely the identity and the element rn / 2 (with Dn as a subgroup of O(2), this is inversion; since it is scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
by −1, it is clear that it commutes with any linear transformation).
For odd n, abstract group Dih2n is isomorphic with the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of Dihn and Z2.
In the case of 2D isometries, this corresponds to adding inversion, giving rotations and mirrors in between the existing ones.
If m divides
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
n, then Dihn has n / m subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of type Dihm, and one subgroup Zm. Therefore the total number of subgroups of Dihn (n ≥ 1), is equal to d(n) + σ(n), where d(n) is the number of positive divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of n and σ(n) is the sum of the positive divisors of n. See list of small groups for the cases n ≤ 8.
Conjugacy classes of reflections
All the reflections are conjugateConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to each other in case n is odd, but they fall into two conjugacy classes if n is even. If we think of the isometries of a regular n-gon: for odd n there are rotations in the group between every pair of mirrors, while for even n only half of the mirrors can be reached from one by these rotations. Geometrically, in an odd polygon every axis of symmetry passes through a vertex and a side, while in an even polygon half the axes pass through two vertices, and half pass through two sides.
Algebraically, this is an instance of the conjugate Sylow theorem
Sylow theorem
In mathematics, specifically in the field of finite group theory, the Sylow theorems are a collection of theorems named after the Norwegian mathematician Ludwig Sylow that give detailed information about the number of subgroups of fixed order that a given finite group contains...
(for n odd): for n odd, each reflection, together with the identity, form a subgroup of order 2, which is a Sylow 2-subgroup (
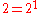 is the maximum power of 2 dividing
is the maximum power of 2 dividing 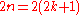 ), while for n even, these order 2 subgroups are not Sylow subgroups because 4 (a higher power of 2) divides the order of the group.
), while for n even, these order 2 subgroups are not Sylow subgroups because 4 (a higher power of 2) divides the order of the group.For n even there is instead an outer automorphism interchanging the two types of reflections (properly, a class of outer automorphisms, which are all conjugate by an inner automorphism).
Automorphism group
The automorphism group of Dihn is isomorphic to the affine groupAffine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
Aff(Z/nZ)
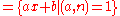 and has order
and has order 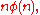 where
where  is Euler's totient function, the number of k in
is Euler's totient function, the number of k in 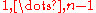 coprime to n.
coprime to n.It can be understood in terms of the generators of a reflection and an elementary rotation (rotation by
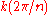 , for k coprime
, for k coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to n); which automorphisms are inner and outer depends on the parity of n.
- For n odd, the dihedral group is centerless, so any element defines a non-trivial inner automorphism; for n even, the rotation by 180° (reflection through the origin) is the non-trivial element of the center.
- Thus for n odd, the inner automorphism group has order 2n, and for n even the inner automorphism group has order n.
- For n odd, all reflections are conjugate; for n even, they fall into two classes (those through two vertices and those through two faces), related by an outer automorphism, which can be represented by rotation by
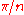 (half the minimal rotation).
(half the minimal rotation). - The rotations are a normal subgroup; conjugation by a reflection changes the sign (direction) of the rotation, but otherwise leaves them unchanged. Thus automorphisms that multiply angles by k (coprime to n) are outer unless

Examples of automorphism groups
Dih9 has 18 inner automorphismInner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
s. As 2D isometry group D9, the group has mirrors at 20° intervals. The 18 inner automorphisms provide rotation of the mirrors by multiples of 20°, and reflections. As isometry group these are all automorphisms. As abstract group there are in addition to these, 36 outer automorphisms, e.g. multiplying angles of rotation by 2.
Dih10 has 10 inner automorphisms. As 2D isometry group D10, the group has mirrors at 18° intervals. The 10 inner automorphisms provide rotation of the mirrors by multiples of 36°, and reflections. As isometry group there are 10 more automorphisms; they are conjugates by isometries outside the group, rotating the mirrors 18° with respect to the inner automorphisms. As abstract group there are in addition to these 10 inner and 10 outer automorphisms, 20 more outer automorphisms, e.g. multiplying rotations by 3.
Compare the values 6 and 4 for Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
, the multiplicative group of integers modulo n
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
for n = 9 and 10, respectively. This triples and doubles the number of automorphisms compared with the two automorphisms as isometries (keeping the order of the rotations the same or reversing the order).
Generalizations
There are several important generalizations of the dihedral groups:- The infinite dihedral groupInfinite dihedral groupIn mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.-Definition:...
is an infinite groupInfinite groupIn group theory, an area of mathematics, an infinite group is a group, of which the underlying set contains an infinite number of elements....
with algebraic structure similar to the finite dihedral groups. It can be viewed as the group of symmetries of the integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. - The orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(2), i.e. the symmetry group of the circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, also has similar properties to the dihedral groups. - The family of generalized dihedral groupGeneralized dihedral groupIn mathematics, the generalized dihedral groups are a family of groups with algebraic structures similar to that of the dihedral groups. They include the finite dihedral groups, the infinite dihedral group, and the orthogonal group O.-Definition:...
s includes both of the examples above, as well as many other groups. - The quasidihedral groupQuasidihedral groupIn mathematics, the quasi-dihedral groups and semi-dihedral groups are non-abelian groups of order a power of 2. For every positive integer n greater than or equal to 4, there are exactly four isomorphism classes of nonabelian groups of order 2n which have a cyclic subgroup of index 2...
s are family of finite groups with similar properties to the dihedral groups.
See also
- Dicyclic group
- Coordinate rotations and reflectionsCoordinate rotations and reflectionsIn geometry, 2D coordinate rotations and reflections are two kinds of Euclidean plane isometries which are related to one another.A rotation in the plane can be formed by composing a pair of reflections. First reflect a point P to its image P′ on the other side of line L1...
- Dihedral group of order 6Dihedral group of order 6The smallest non-abelian group has 6 elements. It is a dihedral group with notation D3 and the symmetric group of degree 3, with notation S3....
- Dihedral group of order 8
- Dihedral symmetry in three dimensionsDihedral symmetry in three dimensionsThis article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
- Dihedral symmetry groups in 3D
- Cycle index of the dihedral group
External links
- Dihedral Group n of Order 2n by Shawn Dudzik, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.