Solvable group
Encyclopedia
In mathematics
, more specifically in the field of group theory
, a solvable group (or soluble group) is a group that can be constructed from abelian group
s using extensions
. That is, a solvable group is a group whose derived series terminates in the trivial subgroup.
Historically, the word "solvable" arose from Galois theory
and the proof
of the general unsolvability of quintic equation. Specifically, a polynomial
equation is solvable by radicals
if and only if the corresponding Galois group
is solvable.
is called solvable if it has a subnormal series whose factor groups are all abelian
, that is, if there are subgroups
such that 
is normal in 
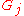, and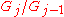 
is an abelian group, for 
.
Or equivalently, if its derived series, the descending normal series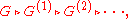
where every subgroup is the commutator subgroup
of the previous one, eventually reaches the trivial subgroup {1} of G. These two definitions are equivalent, since for every group H and every normal subgroup
N of H, the quotient H/N is abelian if and only if
N includes H(1). The least n such that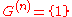
is called the derived length of the solvable group G.
For finite groups, an equivalent definition is that a solvable group is a group with a composition series
all of whose factors are cyclic groups of prime
order
. This is equivalent because a finite abelian group has finite composition length, and every finite simple
abelian group is cyclic of prime order. The Jordan–Hölder theorem guarantees that if one composition series has this property, then all composition series will have this property as well. For the Galois group of a polynomial, these cyclic groups correspond to nth roots (radicals) over some field. The equivalence does not necessarily hold for infinite groups: for example, since every nontrivial subgroup of the group Z of integers under addition is isomorphic
to Z itself, it has no composition series, but the normal series {0,Z}, with its only factor group isomorphic to Z, proves that it is in fact solvable.
A/B will always be abelian if A is abelian. But non-abelian groups may or may not be solvable.
More generally, all nilpotent group
s are solvable. In particular, finite p-groups
are solvable, as all finite p-groups
are nilpotent.
A small example of a solvable, non-nilpotent group is the symmetric group
S3.
In fact, as the smallest simple non-abelian group is A5, (the alternating group of degree 5) it follows that every group with order less than 60 is solvable.
The group S5 is not solvable — it has a composition series {E, A5, S5} (and the Jordan–Hölder theorem states that every other composition series is equivalent to that one), giving factor groups isomorphic to A5 and C2; and A5 is not abelian. Generalizing this argument, coupled with the fact that An is a normal, maximal, non-abelian simple subgroup of Sn for n > 4, we see that Sn is not solvable for n > 4. This is a key step in the proof that for every n > 4 there are polynomial
s of degree n which are not solvable by radicals (Abel–Ruffini theorem
). This property is also used in complexity theory in proof of Barrington's theorem
.
The celebrated Feit–Thompson theorem
states that every finite group of odd order is solvable. In particular this implies that if a finite group is simple, it is either a prime cyclic or of even order.
Any finite group whose every p-Sylow subgroups is cyclic is a semidirect product
of two cyclic groups, in particular solvable. Such groups are called Z-group
s.
Solvability is closed under group extension
:
It is also closed under wreath product:
For any positive integer N, the solvable groups of derived length at most N form a subvariety
of the variety of groups, as they are closed under the taking of homomorphic
images, subalgebra
s, and (direct) products
. The direct product of a sequence of solvable groups with unbounded derived length is not solvable, so the class of all solvable groups is not a variety.
of order
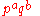
where p and q are prime number
s, and a and b are non-negative integer
s, then G is solvable.
If we restrict ourselves to finitely generated groups, we can consider the following arrangement of classes of groups:
, and every solvable group is a hypoabelian group. The first ordinal α such that G(α) = G(α+1) is called the (transfinite) derived length of the group G, and it has been shown that every ordinal is the derived length of some group .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in the field of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a solvable group (or soluble group) is a group that can be constructed from abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s using extensions
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
. That is, a solvable group is a group whose derived series terminates in the trivial subgroup.
Historically, the word "solvable" arose from Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
and the proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
of the general unsolvability of quintic equation. Specifically, a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation is solvable by radicals
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
if and only if the corresponding Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
is solvable.
Definition
A group is called solvable if it has a subnormal series whose factor groups are all abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, that is, if there are subgroups
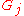such that is normal in , and 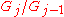is an abelian group, for .Or equivalently, if its derived series, the descending normal series
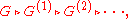
where every subgroup is the commutator subgroup
Commutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of the previous one, eventually reaches the trivial subgroup {1} of G. These two definitions are equivalent, since for every group H and every normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
N of H, the quotient H/N is abelian if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
N includes H(1). The least n such that
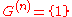is called the derived length of the solvable group G.For finite groups, an equivalent definition is that a solvable group is a group with a composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
all of whose factors are cyclic groups of prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
. This is equivalent because a finite abelian group has finite composition length, and every finite simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
abelian group is cyclic of prime order. The Jordan–Hölder theorem guarantees that if one composition series has this property, then all composition series will have this property as well. For the Galois group of a polynomial, these cyclic groups correspond to nth roots (radicals) over some field. The equivalence does not necessarily hold for infinite groups: for example, since every nontrivial subgroup of the group Z of integers under addition is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to Z itself, it has no composition series, but the normal series {0,Z}, with its only factor group isomorphic to Z, proves that it is in fact solvable.
Examples
All abelian groups are solvable - the quotientQuotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
A/B will always be abelian if A is abelian. But non-abelian groups may or may not be solvable.
More generally, all nilpotent group
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
s are solvable. In particular, finite p-groups
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
are solvable, as all finite p-groups
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
are nilpotent.
A small example of a solvable, non-nilpotent group is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S3.
In fact, as the smallest simple non-abelian group is A5, (the alternating group of degree 5) it follows that every group with order less than 60 is solvable.
The group S5 is not solvable — it has a composition series {E, A5, S5} (and the Jordan–Hölder theorem states that every other composition series is equivalent to that one), giving factor groups isomorphic to A5 and C2; and A5 is not abelian. Generalizing this argument, coupled with the fact that An is a normal, maximal, non-abelian simple subgroup of Sn for n > 4, we see that Sn is not solvable for n > 4. This is a key step in the proof that for every n > 4 there are polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s of degree n which are not solvable by radicals (Abel–Ruffini theorem
Abel–Ruffini theorem
In algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
). This property is also used in complexity theory in proof of Barrington's theorem
NC (complexity)
In complexity theory, the class NC is the set of decision problems decidable in polylogarithmic time on a parallel computer with a polynomial number of processors. In other words, a problem is in NC if there exist constants c and k such that it can be solved in time O using O parallel processors...
.
The celebrated Feit–Thompson theorem
Feit–Thompson theorem
In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by - History : conjectured that every nonabelian finite simple group has even order...
states that every finite group of odd order is solvable. In particular this implies that if a finite group is simple, it is either a prime cyclic or of even order.
Any finite group whose every p-Sylow subgroups is cyclic is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of two cyclic groups, in particular solvable. Such groups are called Z-group
Z-group
In mathematics, especially in the area of algebra known as group theory, the term Z-group refers to a number of distinct types of groups:* in the study of finite groups, a Z-group is a finite groups whose Sylow subgroups are all cyclic....
s.
Properties
Solvability is closed under a number of operations.- If G is solvable, and there is a homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from G onto H, then H is solvable; equivalently (by the first isomorphism theorem), if G is solvable, and N is a normal subgroup of G, then G/N is solvable. - The previous property can be expanded into the following property: G is solvable if and only if both N and G/N are solvable.
- If G is solvable, and H is a subgroup of G, then H is solvable.
- If G and H are solvable, the direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
G × H is solvable.
Solvability is closed under group extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
:
- If H and G/H are solvable, then so is G; in particular, if N and H are solvable, their semidirect productSemidirect productIn mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
is also solvable.
It is also closed under wreath product:
- If G and H are solvable, and X is a G-set, then the wreath productWreath productIn mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
of G and H with respect to X is also solvable.
For any positive integer N, the solvable groups of derived length at most N form a subvariety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
of the variety of groups, as they are closed under the taking of homomorphic
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
images, subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
s, and (direct) products
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
. The direct product of a sequence of solvable groups with unbounded derived length is not solvable, so the class of all solvable groups is not a variety.
Burnside's theorem
Burnside's theorem states that if G is a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
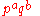
where p and q are prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, and a and b are non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, then G is solvable.
Supersolvable groups
As a strengthening of solvability, a group G is called supersolvable (or supersoluble) if it has an invariant normal series whose factors are all cyclic. Since a normal series has finite length by definition, uncountable groups are not supersolvable. In fact, all supersolvable groups are finitely generated, and an abelian group is supersolvable if and only if it is finitely generated. The alternating group A4 is an example of a finite solvable group that is not supersolvable.If we restrict ourselves to finitely generated groups, we can consider the following arrangement of classes of groups:
- cyclicCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
< abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
< nilpotentNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
< supersolvableSupersolvable groupIn mathematics, a group is supersolvable if it has an invariant normal series where all the factors are cyclic groups. Supersolvability is stronger than the notion of solvability.-Definition:Let G be a group...
< polycyclicPolycyclic groupIn mathematics, a polycyclic group is a solvable group that satisfies the maximal condition on subgroups...
< solvable < finitely generated group.
Virtually solvable groups
A group G is called virtually solvable if it has a solvable subgroup of finite index. This is similar to virtually abelian. Clearly all solvable groups are virtually solvable, since one can just choose the group itself, which has index 1.Hypoabelian
A solvable group is one whose derived series reaches the trivial subgroup at a finite stage. For an infinite group, the finite derived series may not stabilize, but the transfinite derived series always stabilizes. A group whose transfinite derived series reaches the trivial group is called a hypoabelian groupHypoabelian group
*"Hypoabelian group" is an archaic name for an orthogonal group over a field of characteristic 2.*A hypoabelian group can mean a group whose perfect core is trivial...
, and every solvable group is a hypoabelian group. The first ordinal α such that G(α) = G(α+1) is called the (transfinite) derived length of the group G, and it has been shown that every ordinal is the derived length of some group .