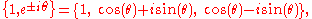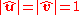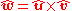Rotation representation (mathematics)
Encyclopedia
In geometry
a rotation representation expresses a rotation
as a mathematical transformation. In physics, this concept extends to classical mechanics
where rotational (or angular) kinematics
is the science of describing with numbers the purely rotational motion of an object.
According to Euler's rotation theorem
the general displacement of a rigid body
(or three-dimensional coordinate system
) with one point fixed is described by a rotation about some axis. This allows the use of rotations to express orientations
as a single rotation from a reference placement in space of the rigid body (or coordinate system). Furthermore, such a rotation may be uniquely described by a minimum of three parameters. However, for various reasons, there are several ways to represent it. Many of these representations use more than the necessary minimum of three parameters, although each of them still has only three degrees of freedom
.
An example where rotation representation is used is in computer vision
, where an automated
observer needs to track a target. Let's consider a rigid body, with an orthogonal
right-handed triad ,
,  , and
, and  of unit vectors fixed to its body (representing the three axes of the object's coordinate system). The basic problem is to specify the orientation of this triad, and hence the rigid body, in terms of the reference coordinate system (in our case the observer's coordinate system).
of unit vectors fixed to its body (representing the three axes of the object's coordinate system). The basic problem is to specify the orientation of this triad, and hence the rigid body, in terms of the reference coordinate system (in our case the observer's coordinate system).
. Specifying the coordinates (scalar components) of this basis in its current (rotated) position, in terms of the reference (non-rotated) coordinate axes, will completely describe the rotation. The three unit vectors ,
,  and
and  which form the rotated basis each consist of 3 coordinates, yielding a total of 9 parameters. These parameters can be written as the elements of a matrix
which form the rotated basis each consist of 3 coordinates, yielding a total of 9 parameters. These parameters can be written as the elements of a matrix  , called a rotation matrix. Typically, the coordinates of each of these vectors are arranged along a column of the matrix.
, called a rotation matrix. Typically, the coordinates of each of these vectors are arranged along a column of the matrix.
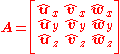
The elements of the rotation matrix are not all independent – as Euler's rotation theorem dictates, the rotation matrix has only three degrees of freedom. The rotation matrix has the following properties:
The angle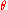 which appears in the eigenvalue expression corresponds to the angle of the Euler axis and angle representation. The eigenvector corresponding with the eigenvalue of 1 is the accompanying Euler axis, since the axis is the only (nonzero) vector which remains unchanged by left-multiplying (rotating) it with the rotation matrix.
which appears in the eigenvalue expression corresponds to the angle of the Euler axis and angle representation. The eigenvector corresponding with the eigenvalue of 1 is the accompanying Euler axis, since the axis is the only (nonzero) vector which remains unchanged by left-multiplying (rotating) it with the rotation matrix.
The above properties are equivalent to:
which is another way of stating that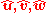 form a 3D orthonormal basis
form a 3D orthonormal basis
. Note that the statements above constitute a total of 6 conditions (the cross product contains 3), leaving the rotation matrix with just 3 degrees of freedom as required.
Two successive rotations represented by matrices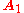 and
and 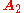 are easily combined as follows:
are easily combined as follows:
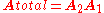 (Note the order, since the vector being rotated is multiplied from the right).
(Note the order, since the vector being rotated is multiplied from the right).
The ease by which vectors can be rotated using a rotation matrix, as well as the ease of combining successive rotations, make the rotation matrix a very useful and popular way to represent rotations, even though it is less concise than other representations.
we know that any rotation can be expressed as a single rotation about some axis. The axis is the unit vector (unique except for sign) which remains unchanged by the rotation. The magnitude of the angle is also unique, with its sign being determined by the sign of the rotation axis.
The axis can be represented as a three-dimensional unit vector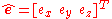 , and the angle by a scalar
, and the angle by a scalar  .
.
Since the axis is normalized, it has only two degrees of freedom
. The angle adds the third degree of freedom to this rotation representation.
One may wish to express rotation as a rotation vector, a non-normalized three-dimensional vector the direction of which specifies the axis, and the length of which is :
:
The rotation vector is in some contexts useful, as it represents a three-dimensional rotation with only three scalar values (its scalar components), representing the three degrees of freedom. This is also true for representations based on sequences of three Euler angles (see below).
If the rotation angle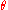 is zero, the axis is not uniquely defined.
is zero, the axis is not uniquely defined.
Combining two successive rotations, each represented by an Euler axis and angle, is not straightforward, and in fact does not satisfy the law of vector addition, which shows that finite rotations are not really vectors at all. It is best to employ the rotation matrix or quaternion notation, calculate the product, and then convert back to Euler axis and angle.
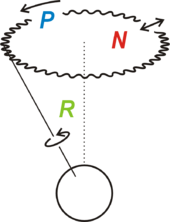
The idea behind Euler rotations is to split the complete rotation of the coordinate system into three simpler constitutive rotations, called Precession
, Nutation
, and intrinsic rotation
, being each one of them an increment on one of the Euler angles
. Notice that the outer matrix will represent a rotation around one of the axes of the reference frame, and the inner matrix represents a rotation around one of the moving frame axis. The middle matrix represent a rotation around an intermediate axis called line of nodes.
Unfortunately, the definition of Euler angles is not unique and in the literature many different conventions are used. These conventions depend on the axes about which the rotations are carried out, and their sequence (since rotations are not commutative
).
The convention being used is usually indicated by specifying the axes about which the consecutive rotations (before being composed) take place, referring to them by index (1, 2, 3) or letter (X, Y, Z). The engineering and robotics communities typically use 3-1-3 Euler angles. Notice that after composing the independent rotations, they do not rotate about their axis anymore. The most external matrix rotates the other two, leaving the second rotation matrix over the line of nodes, and the third one in a frame comoving with the body. There are 3×3×3 = 27 possible combinations of three basic rotations but only 3×2×2 = 12 of them can be used for representing arbitrary 3D rotations as Euler angles. These 12 combinations avoid consecutive rotations around the same axis (such as XXY) which would reduce the degrees of freedom that can be represented.
Therefore Euler angles are never expressed in terms of the external frame, or in terms of the co-moving rotated body frame, but in a mixture. Other conventions (e.g., rotation matrix or quaternions
) are used to avoid this problem.
s (Euler symmetric parameters) have proven very useful in representing rotations due to several advantages above the other representations mentioned in this article.
A quaternion representation of rotation is written as a normalized four-dimensional vector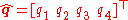 .
.
In terms of the Euler axis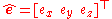
and angle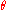
this vector's elements are expressed as follows: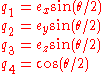
The above definition follows the convention as used in (Wertz 1980) and (Markley 2003). An alternative definition used in some publications defines the "scalar" term as the first quaternion element, with the other elements shifted down one position. (Coutsias 1999), (Schmidt 2001)
Inspection shows that the quaternion parametrization obeys the following constraint: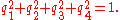
The last term (in our definition) is often called the scalar term, which has its origin in quaternions when understood as the mathematical extension of the complex numbers, written as with
with 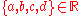 ,
,
and where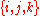 are the hypercomplex number
are the hypercomplex number
s satisfying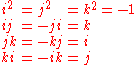
Quaternion multiplication is performed in the same manner as multiplication of complex numbers, except that the order of elements must be taken into account, since multiplication is not commutative. In matrix notation we can write quaternion multiplication as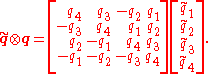
Combining two consecutive quaternion rotations is therefore just as simple as using the rotation matrix. Remember that two successive rotation matrices,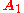 followed by
followed by 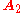 , are combined as follows:
, are combined as follows:
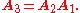
We can represent this quaternion parameters in a similarly concise way. Please note the inverse ordering of quaternion multiplication when compared to matrix multiplication.
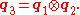
Quaternions are a very popular parametrization due to the following properties:
Like rotation matrices, quaternions must sometimes be re-normalized due to rounding errors, to make sure that they correspond to valid rotations. The computational cost of re-normalizing a quaternion, however, is much less than for normalizing a matrix.
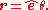
This has a discontinuity at 180° (π radians): each vector, r, with a norm of π radians represent the same rotation as −r.
Similarly, the Gibbs representation can be expressed as follows:

The Gibbs vector has the advantage (or disadvantage, depending on context) that 180° rotations cannot be represented. (Even using floating point
numbers that include infinity, rotation direction cannot be well-defined; for example, naively a 180° rotation about the axis (1, 1, 0) would be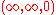 , which is the same representation as 180° rotation about (1, 0.0001, 0).)
, which is the same representation as 180° rotation about (1, 0.0001, 0).)
Modified Rodrigues parameters (MRPs) can be expressed in terms of Euler axis and angle by:

The modified Rodrigues parameterization shares many characteristics with the rotation vector parameterization, including the occurrence of discontinuous jumps in the parameter space when incrementing the rotation.
of a rigid-body relative to some reference frame. The components of this vector are equal to the angles of three simultaneous rotations around the rigid body's intrinsic coordinate system axes, initially aligned with the axes of the reference frame, needed to move the rigid body to its current angular orientation.
Every angular orientation can be represented by a single rotation. Therefore, the three simultaneous orthogonal rotations actually represent a single rotation around a certain axis v and for a certain angle . The orientation and magnitude of SORA are equal to this equivalent single rotation axis v and angle
. The orientation and magnitude of SORA are equal to this equivalent single rotation axis v and angle  , respectively. SORA is therefore the rotation vector, i.e., the vector aligned with the rotation axis and with the length equal to the rotation angle.
, respectively. SORA is therefore the rotation vector, i.e., the vector aligned with the rotation axis and with the length equal to the rotation angle.
Using SORA, angular orientation of a rigid body is indicated with a single rotation equivalent to three simultaneous rotations around the rigid body's intrinsic orthogonal axes initially aligned with the axes of the reference frame. Denoting the angles of the three simultaneous orthogonal rotations with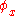 ,
, 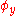 , and
, and 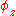 , SORA is equal to:
, SORA is equal to:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
a rotation representation expresses a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
as a mathematical transformation. In physics, this concept extends to classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
where rotational (or angular) kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
is the science of describing with numbers the purely rotational motion of an object.
According to Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
the general displacement of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
(or three-dimensional coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
) with one point fixed is described by a rotation about some axis. This allows the use of rotations to express orientations
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
as a single rotation from a reference placement in space of the rigid body (or coordinate system). Furthermore, such a rotation may be uniquely described by a minimum of three parameters. However, for various reasons, there are several ways to represent it. Many of these representations use more than the necessary minimum of three parameters, although each of them still has only three degrees of freedom
Degrees of freedom (engineering)
In mechanics, degrees of freedom are the set of independent displacements and/or rotations that specify completely the displaced or deformed position and orientation of the body or system...
.
An example where rotation representation is used is in computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, where an automated
Automation
Automation is the use of control systems and information technologies to reduce the need for human work in the production of goods and services. In the scope of industrialization, automation is a step beyond mechanization...
observer needs to track a target. Let's consider a rigid body, with an orthogonal
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
right-handed triad
 ,
,  , and
, and  of unit vectors fixed to its body (representing the three axes of the object's coordinate system). The basic problem is to specify the orientation of this triad, and hence the rigid body, in terms of the reference coordinate system (in our case the observer's coordinate system).
of unit vectors fixed to its body (representing the three axes of the object's coordinate system). The basic problem is to specify the orientation of this triad, and hence the rigid body, in terms of the reference coordinate system (in our case the observer's coordinate system).Rotation matrix
The above mentioned triad of unit vectors is also called a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
. Specifying the coordinates (scalar components) of this basis in its current (rotated) position, in terms of the reference (non-rotated) coordinate axes, will completely describe the rotation. The three unit vectors
 ,
,  and
and  which form the rotated basis each consist of 3 coordinates, yielding a total of 9 parameters. These parameters can be written as the elements of a matrix
which form the rotated basis each consist of 3 coordinates, yielding a total of 9 parameters. These parameters can be written as the elements of a matrix  , called a rotation matrix. Typically, the coordinates of each of these vectors are arranged along a column of the matrix.
, called a rotation matrix. Typically, the coordinates of each of these vectors are arranged along a column of the matrix.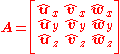
The elements of the rotation matrix are not all independent – as Euler's rotation theorem dictates, the rotation matrix has only three degrees of freedom. The rotation matrix has the following properties:
- A is a realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
, hence each of its rows or columns represents a unit vector. - The eigenvalues of A are
-
- where i is the standard imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
with the property i 2 = −1- The determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of A is +1, equivalent to the product of its eigenvalues. - The traceTrace (linear algebra)In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of A is equivalent to the sum of its eigenvalues.
equivalent to the sum of its eigenvalues.
- The determinant
The angle
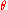 which appears in the eigenvalue expression corresponds to the angle of the Euler axis and angle representation. The eigenvector corresponding with the eigenvalue of 1 is the accompanying Euler axis, since the axis is the only (nonzero) vector which remains unchanged by left-multiplying (rotating) it with the rotation matrix.
which appears in the eigenvalue expression corresponds to the angle of the Euler axis and angle representation. The eigenvector corresponding with the eigenvalue of 1 is the accompanying Euler axis, since the axis is the only (nonzero) vector which remains unchanged by left-multiplying (rotating) it with the rotation matrix.The above properties are equivalent to:
which is another way of stating that
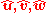 form a 3D orthonormal basis
form a 3D orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
. Note that the statements above constitute a total of 6 conditions (the cross product contains 3), leaving the rotation matrix with just 3 degrees of freedom as required.
Two successive rotations represented by matrices
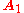 and
and 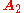 are easily combined as follows:
are easily combined as follows: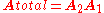 (Note the order, since the vector being rotated is multiplied from the right).
(Note the order, since the vector being rotated is multiplied from the right).The ease by which vectors can be rotated using a rotation matrix, as well as the ease of combining successive rotations, make the rotation matrix a very useful and popular way to represent rotations, even though it is less concise than other representations.
Euler axis and angle (rotation vector)
From Euler's rotation theoremEuler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
we know that any rotation can be expressed as a single rotation about some axis. The axis is the unit vector (unique except for sign) which remains unchanged by the rotation. The magnitude of the angle is also unique, with its sign being determined by the sign of the rotation axis.
The axis can be represented as a three-dimensional unit vector
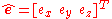 , and the angle by a scalar
, and the angle by a scalar  .
.Since the axis is normalized, it has only two degrees of freedom
Degrees of freedom
Degrees of freedom can mean:* Degrees of freedom , independent displacements and/or rotations that specify the orientation of the body or system...
. The angle adds the third degree of freedom to this rotation representation.
One may wish to express rotation as a rotation vector, a non-normalized three-dimensional vector the direction of which specifies the axis, and the length of which is
 :
:
The rotation vector is in some contexts useful, as it represents a three-dimensional rotation with only three scalar values (its scalar components), representing the three degrees of freedom. This is also true for representations based on sequences of three Euler angles (see below).
If the rotation angle
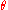 is zero, the axis is not uniquely defined.
is zero, the axis is not uniquely defined.Combining two successive rotations, each represented by an Euler axis and angle, is not straightforward, and in fact does not satisfy the law of vector addition, which shows that finite rotations are not really vectors at all. It is best to employ the rotation matrix or quaternion notation, calculate the product, and then convert back to Euler axis and angle.
Euler rotations

The idea behind Euler rotations is to split the complete rotation of the coordinate system into three simpler constitutive rotations, called Precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
, Nutation
Nutation
Nutation is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behavior of a mechanism...
, and intrinsic rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
, being each one of them an increment on one of the Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
. Notice that the outer matrix will represent a rotation around one of the axes of the reference frame, and the inner matrix represents a rotation around one of the moving frame axis. The middle matrix represent a rotation around an intermediate axis called line of nodes.
Unfortunately, the definition of Euler angles is not unique and in the literature many different conventions are used. These conventions depend on the axes about which the rotations are carried out, and their sequence (since rotations are not commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
).
The convention being used is usually indicated by specifying the axes about which the consecutive rotations (before being composed) take place, referring to them by index (1, 2, 3) or letter (X, Y, Z). The engineering and robotics communities typically use 3-1-3 Euler angles. Notice that after composing the independent rotations, they do not rotate about their axis anymore. The most external matrix rotates the other two, leaving the second rotation matrix over the line of nodes, and the third one in a frame comoving with the body. There are 3×3×3 = 27 possible combinations of three basic rotations but only 3×2×2 = 12 of them can be used for representing arbitrary 3D rotations as Euler angles. These 12 combinations avoid consecutive rotations around the same axis (such as XXY) which would reduce the degrees of freedom that can be represented.
Therefore Euler angles are never expressed in terms of the external frame, or in terms of the co-moving rotated body frame, but in a mixture. Other conventions (e.g., rotation matrix or quaternions
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
) are used to avoid this problem.
Quaternions
QuaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s (Euler symmetric parameters) have proven very useful in representing rotations due to several advantages above the other representations mentioned in this article.
A quaternion representation of rotation is written as a normalized four-dimensional vector
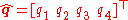 .
.In terms of the Euler axis
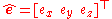
and angle
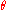
this vector's elements are expressed as follows:
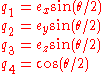
The above definition follows the convention as used in (Wertz 1980) and (Markley 2003). An alternative definition used in some publications defines the "scalar" term as the first quaternion element, with the other elements shifted down one position. (Coutsias 1999), (Schmidt 2001)
Inspection shows that the quaternion parametrization obeys the following constraint:
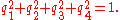
The last term (in our definition) is often called the scalar term, which has its origin in quaternions when understood as the mathematical extension of the complex numbers, written as
 with
with 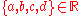 ,
,and where
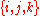 are the hypercomplex number
are the hypercomplex numberHypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
s satisfying
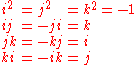
Quaternion multiplication is performed in the same manner as multiplication of complex numbers, except that the order of elements must be taken into account, since multiplication is not commutative. In matrix notation we can write quaternion multiplication as
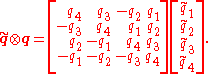
Combining two consecutive quaternion rotations is therefore just as simple as using the rotation matrix. Remember that two successive rotation matrices,
 followed by
followed by 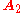 , are combined as follows:
, are combined as follows: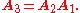
We can represent this quaternion parameters in a similarly concise way. Please note the inverse ordering of quaternion multiplication when compared to matrix multiplication.
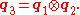
Quaternions are a very popular parametrization due to the following properties:
- More compact than the matrix representation and less susceptible to round-off errorRound-off errorA round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
s - The quaternion elements vary continuously over the unit sphere in
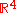 , (denoted by
, (denoted by 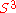 ) as the orientation changes, avoiding discontinuousClassification of discontinuitiesContinuous functions are of utmost importance in mathematics and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there...
) as the orientation changes, avoiding discontinuousClassification of discontinuitiesContinuous functions are of utmost importance in mathematics and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there...
jumps (inherent to three-dimensional parameterizations) - Expression of the rotation matrix in terms of quaternion parameters involves no trigonometric functionTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s - It is simple to combine two individual rotations represented as quaternions using a quaternion product
Like rotation matrices, quaternions must sometimes be re-normalized due to rounding errors, to make sure that they correspond to valid rotations. The computational cost of re-normalizing a quaternion, however, is much less than for normalizing a matrix.
Rodrigues parameters
Rodrigues parameters can be expressed in terms of Euler axis and angle as follows: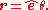
This has a discontinuity at 180° (π radians): each vector, r, with a norm of π radians represent the same rotation as −r.
Similarly, the Gibbs representation can be expressed as follows:

The Gibbs vector has the advantage (or disadvantage, depending on context) that 180° rotations cannot be represented. (Even using floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
numbers that include infinity, rotation direction cannot be well-defined; for example, naively a 180° rotation about the axis (1, 1, 0) would be
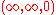 , which is the same representation as 180° rotation about (1, 0.0001, 0).)
, which is the same representation as 180° rotation about (1, 0.0001, 0).)Modified Rodrigues parameters (MRPs) can be expressed in terms of Euler axis and angle by:

The modified Rodrigues parameterization shares many characteristics with the rotation vector parameterization, including the occurrence of discontinuous jumps in the parameter space when incrementing the rotation.
Cayley–Klein parameters
See definition at Wolfram MathworldSimultaneous orthogonal rotations angle
A simultaneous orthogonal rotations angle (SORA) is a vector representing angular orientationOrientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
of a rigid-body relative to some reference frame. The components of this vector are equal to the angles of three simultaneous rotations around the rigid body's intrinsic coordinate system axes, initially aligned with the axes of the reference frame, needed to move the rigid body to its current angular orientation.
Every angular orientation can be represented by a single rotation. Therefore, the three simultaneous orthogonal rotations actually represent a single rotation around a certain axis v and for a certain angle
 . The orientation and magnitude of SORA are equal to this equivalent single rotation axis v and angle
. The orientation and magnitude of SORA are equal to this equivalent single rotation axis v and angle  , respectively. SORA is therefore the rotation vector, i.e., the vector aligned with the rotation axis and with the length equal to the rotation angle.
, respectively. SORA is therefore the rotation vector, i.e., the vector aligned with the rotation axis and with the length equal to the rotation angle.Using SORA, angular orientation of a rigid body is indicated with a single rotation equivalent to three simultaneous rotations around the rigid body's intrinsic orthogonal axes initially aligned with the axes of the reference frame. Denoting the angles of the three simultaneous orthogonal rotations with
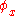 ,
, 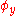 , and
, and 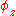 , SORA is equal to:
, SORA is equal to:-

where v and are the equivalent single rotation axis and angle respectively, equal to:
are the equivalent single rotation axis and angle respectively, equal to:
-

-
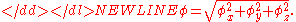
Rotors in a geometric algebra
The formalism of geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
(GA) provides an extension and interpretation of the quaternion method. Central to GA is the geometric product of vectors, an extension of the traditional inner and cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
s, given by
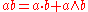
where the symbol denotes the outer productOuter productIn linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
denotes the outer productOuter productIn linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
. This product of vectors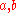 produces two terms: a scalar part from the inner product and a bivectorBivectorIn mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
produces two terms: a scalar part from the inner product and a bivectorBivectorIn mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
part from the outer product. This bivector describes the plane perpendicular to what the cross product of the vectors would return.
Bivectors in GA have some unusual properties compared to vectors. Under the geometric product, bivectors have negative square: the bivector describes the
describes the  -plane. Its square is
-plane. Its square is 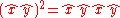 . Because the unit basis vectors are orthogonal to each other, the geometric product reduces to the antisymmetric outer product –
. Because the unit basis vectors are orthogonal to each other, the geometric product reduces to the antisymmetric outer product –  and
and 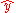 can be swapped freely at the cost of a factor of −1. The square reduces to
can be swapped freely at the cost of a factor of −1. The square reduces to 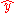 since the basis vectors themselves square to +1.
since the basis vectors themselves square to +1.
This result holds generally for all bivectors, and as a result the bivector plays a role similar to the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. Geometric algebra uses bivectors in its analogue to the quaternion, the rotor, given by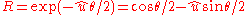 , where
, where  is a unit bivector that describes the plane of rotationPlane of rotationIn geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
is a unit bivector that describes the plane of rotationPlane of rotationIn geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
. Because squares to −1, the power series expansion of
squares to −1, the power series expansion of  generates the trigonometric functionTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
generates the trigonometric functionTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s. The rotation formula that maps a vector to a rotated vector
to a rotated vector 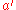 is then
is then
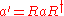
where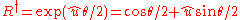 is the reverse of
is the reverse of  (reversing the order of the vectors in
(reversing the order of the vectors in  is equivalent to changing its sign).
is equivalent to changing its sign).
Example. A rotation about the axis can be accomplished by converting
can be accomplished by converting  to its dual bivector,
to its dual bivector,  , where
, where  is the unit volume element, the only trivector in three-dimensional space. The result is
is the unit volume element, the only trivector in three-dimensional space. The result is 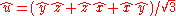 . In three-dimensional space, however, it is often simpler to leave the expression for
. In three-dimensional space, however, it is often simpler to leave the expression for 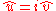 , using the fact that
, using the fact that 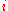 commutes with all objects in 3D and also squares to −1. A rotation of the
commutes with all objects in 3D and also squares to −1. A rotation of the  vector in this plane by an angle
vector in this plane by an angle 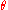 is then
is then
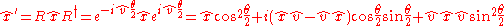
Recognizing that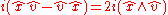 and that
and that 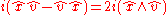 is the reflection of
is the reflection of  about the plane perpendicular to
about the plane perpendicular to  gives a geometric interpretation to the rotation operation: the rotation preserves the components that are parallel to
gives a geometric interpretation to the rotation operation: the rotation preserves the components that are parallel to  and changes only those that are perpendicular. The terms are then computed:
and changes only those that are perpendicular. The terms are then computed:
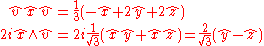
The result of the rotation is then

A simple check on this result is the angle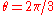 . Such a rotation should map the
. Such a rotation should map the  to
to 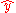 . Indeed, the rotation reduces to
. Indeed, the rotation reduces to
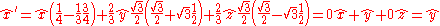
exactly as expected. This rotation formula is valid not only for vectors but for any multivectorMultivectorIn multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
. In addition, when Euler angles are used, the complexity of the operation is much reduced. Compounded rotations come from multiplying the rotors, so the total rotor from Euler angles is
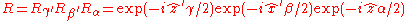
but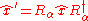 and
and 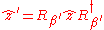 . These rotors come back out of the exponentials like so:
. These rotors come back out of the exponentials like so:
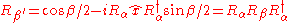
where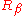 refers to rotation in the original coordinates. Similarly for the
refers to rotation in the original coordinates. Similarly for the 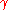 rotation,
rotation, 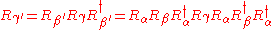 . Noting that
. Noting that 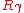 and
and 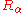 commute (rotations in the same plane must commute), and the total rotor becomes
commute (rotations in the same plane must commute), and the total rotor becomes
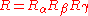
Thus, the compounded rotations of Euler angles become a series of equivalent rotations in the original fixed frame.
While rotors in geometric algebra work almost identically to quaternions in three dimensions, the power of this formalism is its generality: this method is appropriate and valid in spaces with any number of dimensions. In 3D, rotations have three degrees of freedom, a degree for each linearly independent plane (bivector) the rotation can take place in. It has been known that pairs of quaternions can be used to generate rotations in 4D, yielding six degrees of freedom, and the geometric algebra approach verifies this result: in 4D, there are six linearly independent bivectors that can be used as the generators of rotations.
Conversion formulae between representations
Rotation matrix ↔ Euler angles
The Euler angles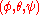 can be extracted from the rotation matrix
can be extracted from the rotation matrix  by inspecting the rotation matrix in analytical form.
by inspecting the rotation matrix in analytical form.
Using the x-convention, the 3-1-3 Euler angles ,
, 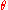 and
and 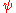 (around the
(around the  ,
,  and again the
and again the  -axis) can be obtained as follows:
-axis) can be obtained as follows:
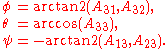
Note that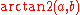 is equivalent to
is equivalent to  where it also takes into account the quadrant in which the point
where it also takes into account the quadrant in which the point 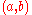 is in; see atan2Atan2In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
is in; see atan2Atan2In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
.
When implementing the conversion, one has to take into account several situations:- There are generally two solutions in (−π,π〉3 interval. The above formula works only when
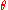 is from the interval 〈0,π)3.
is from the interval 〈0,π)3. - For special case
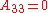 ,
, 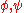 shall be derived from
shall be derived from 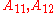 .
. - There is infinitely many but countably many solutions outside of interval (−π,π〉3.
- Whether all mathematical solutions apply for given application depends on the situation.
The rotation matrix is generated from the Euler angles by multiplying the three matrices generated by rotations about the axes.
is generated from the Euler angles by multiplying the three matrices generated by rotations about the axes.
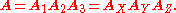
The axes of the rotation depend on the specific convention being used. For the x-convention the rotations are about the ,
,  and
and  axes with angles
axes with angles  ,
, 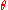 and
and 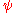 , the individual matrices are as follows:
, the individual matrices are as follows:
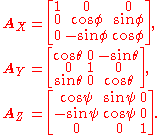
This yields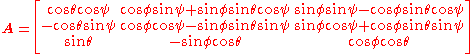
Note: This is valid for a right-hand system, which is the convention used in almost all engineering and physics disciplines.
Rotation matrix ↔ Euler axis/angle
If the Euler angle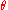 is not a multiple of
is not a multiple of  , the Euler axis
, the Euler axis 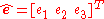 and angle
and angle 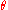 can be computed from the elements of the rotation matrix
can be computed from the elements of the rotation matrix  as follows:
as follows: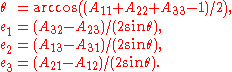
Alternatively, the following method can be used:
Eigen-decomposition of the rotation matrix yields the eigenvalues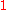 , and
, and  .
.
The Euler axis is the eigenvector corresponding to the eigenvalue of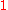 , and the
, and the 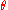 can be computed from the remaining eigenvalues.
can be computed from the remaining eigenvalues.
The Euler axis can be also found using Singular Value Decomposition since it is the normalized vector spanning the null-space of the matrix .
.
To convert the other way the rotation matrix corresponding to an Euler axis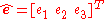 and angle
and angle 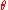 can be computed according to the Rodrigues' rotation formulaRodrigues' rotation formulaIn the theory of three-dimensional rotation, Rodrigues' rotation formula is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation...
can be computed according to the Rodrigues' rotation formulaRodrigues' rotation formulaIn the theory of three-dimensional rotation, Rodrigues' rotation formula is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation...
(with appropriate modification) as follows:

with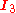 the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, and
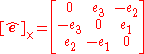
is the cross-product matrix.
Rotation matrix ↔ quaternion
When computing a quaternion from the rotation matrix there is a sign ambiguity, since and
and  represent the same rotation.
represent the same rotation.
One way of computing the quaternion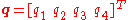 from the rotation matrix
from the rotation matrix  is as follows:
is as follows:
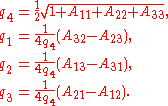
There are three other mathematically equivalent ways to compute . Numerical inaccuracy can be reduced by avoiding situations in which the denominator is close to zero. One of the other three methods looks as follows:
. Numerical inaccuracy can be reduced by avoiding situations in which the denominator is close to zero. One of the other three methods looks as follows:
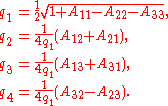
The rotation matrix corresponding to the quaternion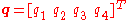 can be computed as follows:
can be computed as follows:
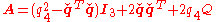
with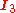 the identity matrix, and
the identity matrix, and
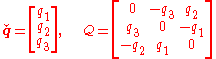
which gives
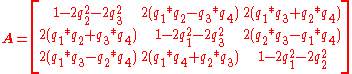
or equivalently
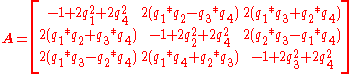 .
.
Euler angles ↔ quaternion
We will consider the x-convention 3-1-3 Euler Angles for the following algorithm. The terms of the algorithm depend on the convention used.
We can compute the quaternion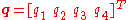 from the Euler angles
from the Euler angles 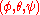 as follows:
as follows:
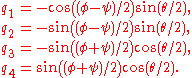
Given the rotation quaternion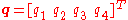 , the x-convention 3-1-3 Euler angles
, the x-convention 3-1-3 Euler angles 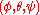 can be computed by
can be computed by
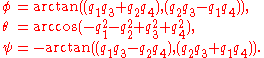
Euler axis/angle ↔ quaternion
Given the Euler axis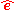 and angle
and angle 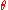 , the quaternion
, the quaternion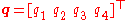
can be computed by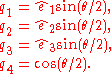
Given the rotation quaternion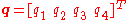 , define
, define 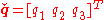 . Then the Euler axis
. Then the Euler axis 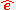 and angle
and angle 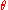 can be computed by
can be computed by
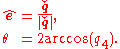
Rotation matrix ↔ Angular velocities
The angular velocity vector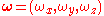 can be extracted from the derivative of the rotation matrix
can be extracted from the derivative of the rotation matrix 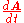 by the following relation:
by the following relation: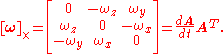
The derivation is adapted from as follows:
For any vector consider
consider 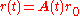 and differentiate it:
and differentiate it: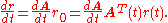
The derivative of a vector is the linear velocity of its tip. Since A is a rotation matrix, by definition the length of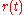 is always equal to the length of
is always equal to the length of  , and hence it does not change with time. Thus, when
, and hence it does not change with time. Thus, when 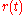 rotates, its tip moves along a circle, and the linear velocity of its tip is tangential to the circle, i.e. always perpendicular to
rotates, its tip moves along a circle, and the linear velocity of its tip is tangential to the circle, i.e. always perpendicular to 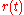 . In this specific case, the relationship between the linear velocity vector and the angular velocity vector is
. In this specific case, the relationship between the linear velocity vector and the angular velocity vector is
 (see circular motionCircular motionIn physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
(see circular motionCircular motionIn physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
and Cross product).
By the transitivityTransitivity (mathematics)-In grammar:* Intransitive verb* Transitive verb, when a verb takes an object* Transitivity -In logic and mathematics:* Arc-transitive graph* Edge-transitive graph* Ergodic theory, a group action that is metrically transitive* Vertex-transitive graph...
of the above mentioned equations,
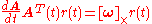
which implies (QEDQEDQED may refer to:*Q.E.D., from the Latin quod erat demonstrandum, used at the end of a definitive proof*Quantum electrodynamics, a field of physics...
),
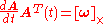
Quaternion ↔ Angular velocities
The angular velocity vector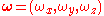 can be obtained from the derivative of the quaternion
can be obtained from the derivative of the quaternion 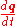 as follows:
as follows: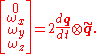
Conversely, the derivative of the quaternion is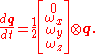
See also
- Charts on SO(3)Charts on SO(3)In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...
- Euler filterEuler filterIn computer graphics, an Euler filter is a filter intended to remove discontinuities from animation data sets in which rotation is expressed in terms of Euler angles....
- Euler–Rodrigues parameters
- Orientation (geometry)Orientation (geometry)In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
- Rotation around a fixed axisRotation around a fixed axisRotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...
- Rotation (mathematics)Rotation (mathematics)In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
- Rotation operator (vector space)Rotation operator (vector space)This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
External links
- EuclideanSpace has a wealth of information on rotation representation
- Q36. How do I generate a rotation matrix from Euler angles? and Q37. How do I convert a rotation matrix to Euler angles? — The Matrix and Quaternions FAQ
- Imaginary numbers are not Real - the Geometric Algebra of Spacetime - Section "Rotations and Geometric Algebra" derives and applies the rotor description of rotations
- Starlino's DCM Tutorial - Direction cosine matrix theory tutorial and applications. Space orientation estimation algorithm using accelerometer, gyroscope and magnetometer IMU devices. Using complimentary filter (popular alternative to Kalman filter) with DCM matrix.
- There are generally two solutions in (−π,π〉3 interval. The above formula works only when
-
-