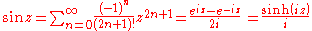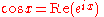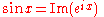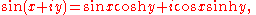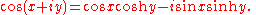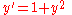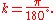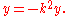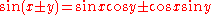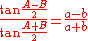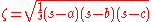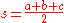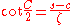Trigonometric function
Encyclopedia
In mathematics
, the trigonometric functions (also called circular functions) are function
s of an angle
. They are used to relate the angles of a triangle to the lengths of the sides of a triangle. Trigonometric functions are important in the study of triangles and modeling periodic phenomena, among many other applications.
The most familiar trigonometric functions are the sine
, cosine, and tangent. In the context of the standard unit circle with radius 1, where a triangle is formed by a ray originating at the origin and making some angle with the x-axis, the sine of the angle gives the length of the y-component (rise) of the triangle, the cosine gives the length of the x-component (run), and the tangent function gives the slope (y-component divided by the x-component). More precise definitions are detailed below. Trigonometric functions are commonly defined as ratio
s of two sides of a right triangle containing the angle, and can equivalently be defined as the lengths of various line segments from a unit circle
. More modern definitions express them as infinite series
or as solutions of certain differential equation
s, allowing their extension to arbitrary positive and negative values and even to complex number
s.
Trigonometric functions have a wide range of uses including computing unknown lengths and angles in triangle
s (often right triangle
s). In this use, trigonometric functions are used, for instance, in navigation, engineering, and physics. A common use in elementary physics is resolving a vector
into Cartesian
coordinates. The sine and cosine functions are also commonly used to model periodic function
phenomena such as sound
and light waves, the position and velocity of harmonic oscillators, sunlight intensity and day length, and average temperature variations through the year.
In modern usage, there are six basic trigonometric functions, tabulated here with equations that relate them to one another. Especially with the last four, these relations are often taken as the definitions of those functions, but one can define them equally well geometrically, or by other means, and then derive these relations.
 The notion that there should be some standard correspondence between the lengths of the sides of a triangle and the angles of the triangle comes as soon as one recognizes that similar triangles
The notion that there should be some standard correspondence between the lengths of the sides of a triangle and the angles of the triangle comes as soon as one recognizes that similar triangles
maintain the same ratios between their sides. That is, for any similar triangle the ratio of the hypotenuse
(for example) and another of the sides remains the same. If the hypotenuse is twice as long, so are the sides. It is these ratios that the trigonometric functions express.
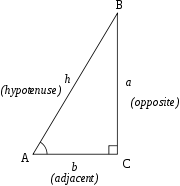
To define the trigonometric functions for the angle A, start with any right triangle
that contains the angle A. The three sides of the triangle are named as follows:
In ordinary Euclidean geometry
, according to the triangle postulate
the inside angles of every triangle total 180°
(π radian
s). Therefore, in a right-angled triangle, the two non-right angles total 90° (π/2 radians), so each of these angles must be in the range of (0°,90°) as expressed in interval notation. The following definitions apply to angles in this 0° – 90° range. They can be extended to the full set of real arguments by using the unit circle, or by requiring certain symmetries and that they be periodic function
s. For example, the figure shows sin θ for angles θ, π − θ, π + θ, and 2π − θ depicted on the unit circle (top) and as a graph (bottom). The value of the sine repeats itself apart from sign in all four quadrants, and if the range of θ is extended to additional rotations, this behavior repeats periodically with a period 2π.
The trigonometric functions are summarized in the following table and described in more detail below. The angle θ is the angle between the hypotenuse and the adjacent line – the angle at A in the accompanying diagram.
of an angle is the ratio of the length of the opposite side
to the length of the hypotenuse. (The word comes from the Latin sinus for gulf or bay, since, given a unit circle, it is the side of the triangle on which the angle opens). In our case

Note that this ratio does not depend on size of the particular right triangle chosen, as long as it contains the angle A, since all such triangles are similar
.
The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse: so called because it is the sine of the complementary or co-angle. In our case

The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side: so called because it can be represented as a line segment tangent to the circle, that is the line that touches the circle, from Latin linea tangens or touching line (cf. tangere, to touch). In our case
The acronyms "SOHCAHTOA" and "OHSAHCOAT" are commonly used mnemonic
s for these ratios.
The cosecant csc(A), or cosec(A), is the reciprocal
of sin(A), i.e. the ratio of the length of the hypotenuse to the length of the opposite side:
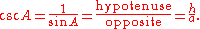
The secant sec(A) is the reciprocal
of cos(A), i.e. the ratio of the length of the hypotenuse to the length of the adjacent side:
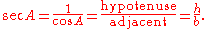
It is so called because it represents the line that cuts the circle (from Latin: secare, to cut).
The cotangent cot(A) is the reciprocal
of tan(A), i.e. the ratio of the length of the adjacent side to the length of the opposite side: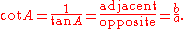
of a line segment relative to horizontal. The slope is commonly taught as "rise over run" or . The three main trigonometric functions are commonly taught in the order sine, cosine, tangent. With a line segment length of 1 (as in a unit circle
), the following mnemonic devices show the correspondence of definitions:
This shows the main use of tangent and arctangent: converting between the two ways of telling the slant of a line, i.e., angles and slopes. (Note that the arctangent or "inverse tangent" is not to be confused with the cotangent, which is cosine divided by sine.)
While the length of the line segment makes no difference for the slope (the slope does not depend on the length of the slanted line), it does affect rise and run. To adjust and find the actual rise and run when the line does not have a length of 1, just multiply the sine and cosine by the line length. For instance, if the line segment has length 5, the run at an angle of 7° is 5 cos(7°)
, the circle
of radius one centered at the origin. The unit circle definition provides little in the way of practical calculation; indeed it relies on right triangles for most angles.
The unit circle definition does, however, permit the definition of the trigonometric functions for all positive and negative arguments, not just for angles between 0 and π/2 radian
s.
It also provides a single visual picture that encapsulates at once all the important triangles. From the Pythagorean theorem
the equation for the unit circle is:
In the picture, some common angles, measured in radians, are given. Measurements in the counterclockwise direction are positive angles and measurements in the clockwise direction are negative angles.
Let a line through the origin, making an angle of θ with the positive half of the x-axis, intersect the unit circle. The x- and y-coordinates of this point of intersection are equal to cos θ and sin θ, respectively.
The triangle in the graphic enforces the formula; the radius is equal to the hypotenuse and has length 1, so we have sin θ = y/1 and cos θ = x/1. The unit circle can be thought of as a way of looking at an infinite number of triangles by varying the lengths of their legs but keeping the lengths of their hypotenuses equal to 1.
Note that these values can easily be memorized in the form
but the angles are not equally spaced.
The values for 15°, 54° and 75° are slightly more complicated.
For angles greater than 2π or less than −2π, simply continue to rotate around the circle; sine and cosine are periodic function
s with period 2π:
for any angle θ and any integer
k.
The smallest positive period of a periodic function is called the primitive period of the function.
The primitive period of the sine or cosine is a full circle, i.e. 2π radians or 360 degrees.
Above, only sine and cosine were defined directly by the unit circle, but other trigonometric functions can be defined by:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the trigonometric functions (also called circular functions) are function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s of an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
. They are used to relate the angles of a triangle to the lengths of the sides of a triangle. Trigonometric functions are important in the study of triangles and modeling periodic phenomena, among many other applications.
The most familiar trigonometric functions are the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
, cosine, and tangent. In the context of the standard unit circle with radius 1, where a triangle is formed by a ray originating at the origin and making some angle with the x-axis, the sine of the angle gives the length of the y-component (rise) of the triangle, the cosine gives the length of the x-component (run), and the tangent function gives the slope (y-component divided by the x-component). More precise definitions are detailed below. Trigonometric functions are commonly defined as ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s of two sides of a right triangle containing the angle, and can equivalently be defined as the lengths of various line segments from a unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. More modern definitions express them as infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
or as solutions of certain differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, allowing their extension to arbitrary positive and negative values and even to complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
Trigonometric functions have a wide range of uses including computing unknown lengths and angles in triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s (often right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s). In this use, trigonometric functions are used, for instance, in navigation, engineering, and physics. A common use in elementary physics is resolving a vector
Vector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
into Cartesian
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
coordinates. The sine and cosine functions are also commonly used to model periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
phenomena such as sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
and light waves, the position and velocity of harmonic oscillators, sunlight intensity and day length, and average temperature variations through the year.
In modern usage, there are six basic trigonometric functions, tabulated here with equations that relate them to one another. Especially with the last four, these relations are often taken as the definitions of those functions, but one can define them equally well geometrically, or by other means, and then derive these relations.
Right-angled triangle definitions

Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
maintain the same ratios between their sides. That is, for any similar triangle the ratio of the hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
(for example) and another of the sides remains the same. If the hypotenuse is twice as long, so are the sides. It is these ratios that the trigonometric functions express.
To define the trigonometric functions for the angle A, start with any right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
that contains the angle A. The three sides of the triangle are named as follows:
- The hypotenuse is the side opposite the right angle, in this case side h. The hypotenuse is always the longest side of a right-angled triangle.
- The opposite side is the side opposite to the angle we are interested in (angle A), in this case side a.
- The adjacent side is the side having both the angles of interest (angle A and right-angle C), in this case side b.
In ordinary Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, according to the triangle postulate
Triangle postulate
In Euclidean geometry, the triangle postulate states that the sum of the angles of a triangle is two right angles. This postulate is equivalent to the parallel postulate...
the inside angles of every triangle total 180°
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
(π radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s). Therefore, in a right-angled triangle, the two non-right angles total 90° (π/2 radians), so each of these angles must be in the range of (0°,90°) as expressed in interval notation. The following definitions apply to angles in this 0° – 90° range. They can be extended to the full set of real arguments by using the unit circle, or by requiring certain symmetries and that they be periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s. For example, the figure shows sin θ for angles θ, π − θ, π + θ, and 2π − θ depicted on the unit circle (top) and as a graph (bottom). The value of the sine repeats itself apart from sign in all four quadrants, and if the range of θ is extended to additional rotations, this behavior repeats periodically with a period 2π.
The trigonometric functions are summarized in the following table and described in more detail below. The angle θ is the angle between the hypotenuse and the adjacent line – the angle at A in the accompanying diagram.
| Function | Abbreviation | Description | Identities (using radian Radian Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit... s) |
|---|---|---|---|
| Sine | sin | opposite / hypotenuse | 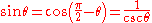 |
| Cosine | cos | adjacent / hypotenuse | 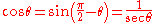 |
| Tangent | tan (or tg) | opposite / adjacent |  |
| Cotangent | cot (or ctg or ctn) | adjacent / opposite |  |
| Secant | sec | hypotenuse / adjacent | 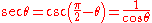 |
| Cosecant | csc (or cosec) | hypotenuse / opposite |  |


Sine, cosine, and tangent
The sineSine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
of an angle is the ratio of the length of the opposite side
Cathetus
In a right triangle, the cathetus , commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called the periphrasis . The side opposite the right angle is the hypotenuse...
to the length of the hypotenuse. (The word comes from the Latin sinus for gulf or bay, since, given a unit circle, it is the side of the triangle on which the angle opens). In our case

Note that this ratio does not depend on size of the particular right triangle chosen, as long as it contains the angle A, since all such triangles are similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
.
The cosine of an angle is the ratio of the length of the adjacent side to the length of the hypotenuse: so called because it is the sine of the complementary or co-angle. In our case

The tangent of an angle is the ratio of the length of the opposite side to the length of the adjacent side: so called because it can be represented as a line segment tangent to the circle, that is the line that touches the circle, from Latin linea tangens or touching line (cf. tangere, to touch). In our case

The acronyms "SOHCAHTOA" and "OHSAHCOAT" are commonly used mnemonic
Mnemonic
A mnemonic , or mnemonic device, is any learning technique that aids memory. To improve long term memory, mnemonic systems are used to make memorization easier. Commonly encountered mnemonics are often verbal, such as a very short poem or a special word used to help a person remember something,...
s for these ratios.
Reciprocal functions
The remaining three functions are best defined using the above three functions.The cosecant csc(A), or cosec(A), is the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of sin(A), i.e. the ratio of the length of the hypotenuse to the length of the opposite side:
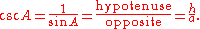
The secant sec(A) is the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of cos(A), i.e. the ratio of the length of the hypotenuse to the length of the adjacent side:
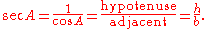
It is so called because it represents the line that cuts the circle (from Latin: secare, to cut).
The cotangent cot(A) is the reciprocal
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of tan(A), i.e. the ratio of the length of the adjacent side to the length of the opposite side:
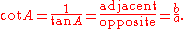
Slope definitions
Equivalent to the right-triangle definitions, the trigonometric functions can also be defined in terms of the rise, run, and slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of a line segment relative to horizontal. The slope is commonly taught as "rise over run" or . The three main trigonometric functions are commonly taught in the order sine, cosine, tangent. With a line segment length of 1 (as in a unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
), the following mnemonic devices show the correspondence of definitions:
- "Sine is first, rise is first" meaning that Sine takes the angle of the line segment and tells its vertical rise when the length of the line is 1.
- "Cosine is second, run is second" meaning that Cosine takes the angle of the line segment and tells its horizontal run when the length of the line is 1.
- "Tangent combines the rise and run" meaning that Tangent takes the angle of the line segment and tells its slope; or alternatively, tells the vertical rise when the line segment's horizontal run is 1.
This shows the main use of tangent and arctangent: converting between the two ways of telling the slant of a line, i.e., angles and slopes. (Note that the arctangent or "inverse tangent" is not to be confused with the cotangent, which is cosine divided by sine.)
While the length of the line segment makes no difference for the slope (the slope does not depend on the length of the slanted line), it does affect rise and run. To adjust and find the actual rise and run when the line does not have a length of 1, just multiply the sine and cosine by the line length. For instance, if the line segment has length 5, the run at an angle of 7° is 5 cos(7°)
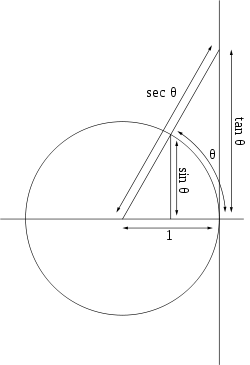
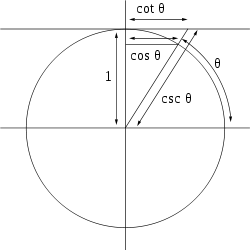
Unit-circle definitions
The six trigonometric functions can also be defined in terms of the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
, the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
of radius one centered at the origin. The unit circle definition provides little in the way of practical calculation; indeed it relies on right triangles for most angles.
The unit circle definition does, however, permit the definition of the trigonometric functions for all positive and negative arguments, not just for angles between 0 and π/2 radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s.
It also provides a single visual picture that encapsulates at once all the important triangles. From the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
the equation for the unit circle is:
In the picture, some common angles, measured in radians, are given. Measurements in the counterclockwise direction are positive angles and measurements in the clockwise direction are negative angles.
Let a line through the origin, making an angle of θ with the positive half of the x-axis, intersect the unit circle. The x- and y-coordinates of this point of intersection are equal to cos θ and sin θ, respectively.
The triangle in the graphic enforces the formula; the radius is equal to the hypotenuse and has length 1, so we have sin θ = y/1 and cos θ = x/1. The unit circle can be thought of as a way of looking at an infinite number of triangles by varying the lengths of their legs but keeping the lengths of their hypotenuses equal to 1.
Note that these values can easily be memorized in the form
but the angles are not equally spaced.
The values for 15°, 54° and 75° are slightly more complicated.
For angles greater than 2π or less than −2π, simply continue to rotate around the circle; sine and cosine are periodic function
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s with period 2π:
for any angle θ and any integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
k.
The smallest positive period of a periodic function is called the primitive period of the function.
The primitive period of the sine or cosine is a full circle, i.e. 2π radians or 360 degrees.
Above, only sine and cosine were defined directly by the unit circle, but other trigonometric functions can be defined by:
-

So :- The primitive period of the secant, or cosecant is also a full circle, i.e. 2π radians or 360 degrees.
- The primitive period of the tangent or cotangent is only a half-circle, i.e. π radians or 180 degrees.
The image at right includes a graph of the tangent function.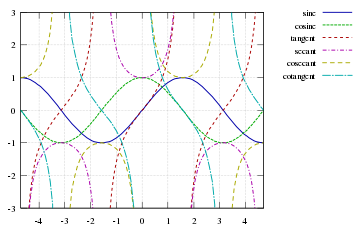
- Its θ-intercepts correspond to those of sin(θ) while its undefined values correspond to the θ-intercepts of cos(θ).
- The function changes slowly around angles of kπ, but changes rapidly at angles close to (k + 1/2)π.
- The graph of the tangent function also has a vertical asymptoteAsymptoteIn analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
at θ = (k + 1/2)π, the θ-intercepts of the cosine function, because the function approaches infinity as θ approaches (k + 1/2)π from the left and minus infinity as it approaches (k + 1/2)π from the right.
Alternatively, all of the basic trigonometric functions can be defined in terms of a unit circle centered at O (as shown in the picture to the right), and similar such geometric definitions were used historically.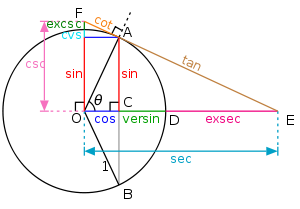
- In particular, for a chord AB of the circle, where θ is half of the subtended angle, sin(θ) is AC (half of the chord), a definition introduced in IndiaIndiaIndia , officially the Republic of India , is a country in South Asia. It is the seventh-largest country by geographical area, the second-most populous country with over 1.2 billion people, and the most populous democracy in the world...
(see history). - cos(θ) is the horizontal distance OC, and versinVersineThe versine or versed sine, versin, is a trigonometric function equal to and 2sin2. It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used...
(θ) = 1 − cos(θ) is CD. - tan(θ) is the length of the segment AE of the tangent line through A, hence the word tangentTangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
for this function. cot(θ) is another tangent segment, AF. - sec(θ) = OE and csc(θ) = OF are segments of secant lineSecant lineA secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
s (intersecting the circle at two points), and can also be viewed as projections of OA along the tangent at A to the horizontal and vertical axes, respectively. - DE is exsec(θ) = sec(θ) − 1 (the portion of the secant outside, or ex, the circle).
- From these constructions, it is easy to see that the secant and tangent functions diverge as θ approaches π/2 (90 degrees) and that the cosecant and cotangent diverge as θ approaches zero. (Many similar constructions are possible, and the basic trigonometric identities can also be proven graphically.)
Series definitions
Using only geometry and properties of limits Limit of a functionIn mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
Limit of a functionIn mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
, it can be shown that the derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of sine is cosine and the derivative of cosine is the negative of sine. (Here, and generally in calculusCalculusCalculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, all angles are measured in radianRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s; see also the significance of radians below.) One can then use the theory of Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
to show that the following identities hold for all real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s x:
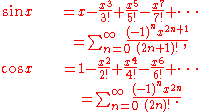
These identities are sometimes taken as the definitions of the sine and cosine function. They are often used as the starting point in a rigorous treatment of trigonometric functions and their applications (e.g., in Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
), since the theory of infinite seriesSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
can be developed, independent of any geometric considerations, from the foundations of the real number systemReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. The differentiabilityDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and continuityContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of these functions are then established from the series definitions alone.
Combining these two series gives Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
: cos x + i sin x = eix.
Other series can be found. For the following trigonometric functions:- Un is the nth up/down number,
- Bn is the nth Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
, and - En (below) is the nth Euler number.
Tangent-
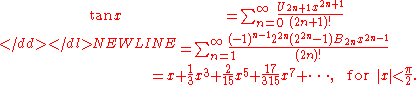
When this series for the tangent function is expressed in a form in which the denominators are the corresponding factorials, the numerators, called the "tangent numbers", have a combinatorialCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
interpretation: they enumerate alternating permutations of finite sets of odd cardinality.
Cosecant-

Secant-
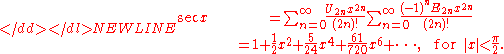
When this series for the secant function is expressed in a form in which the denominators are the corresponding factorials, the numerators, called the "secant numbers", have a combinatorialCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
interpretation: they enumerate alternating permutations of finite sets of even cardinality.
Cotangent-

From a theorem in complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, there is a unique analytic continuationAnalytic continuationIn complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of this real function to the domain of complex numbers. They have the same Taylor series, and so the trigonometric functions are defined on the complex numbers using the Taylor series above.
There is a series representation as partial fraction expansion where just translated reciprocal functionMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s are summed up, such that the poles of the cotangent function and the reciprocal functions match:-
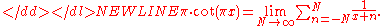
This identity can be proven with the HerglotzGustav HerglotzGustav Herglotz was a German mathematician. He is best known for his works on the theory of relativity and seismology....
trick.
By combining the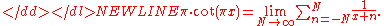 -th with the
-th with the  -th term, it can be expressed as an absolutely convergentAbsolute convergenceIn mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
-th term, it can be expressed as an absolutely convergentAbsolute convergenceIn mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
series:
Relationship to exponential function and complex numbers
It can be shown from the series definitions that the sine and cosine functions are the imaginary.gif) Complex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
Complex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
and real parts, respectively, of the complex exponential function when its argument is purely imaginary:

This identity is called Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
. In this way, trigonometric functions become essential in the geometric interpretation of complex analysis. For example, with the above identity, if one considers the unit circle in the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, parametrized by e ix, and as above, we can parametrize this circle in terms of cosines and sines, the relationship between the complex exponential and the trigonometric functions becomes more apparent.
Furthermore, this allows for the definition of the trigonometric functions for complex arguments z:
where i 2 = −1. The sine and cosine defined by this are entire functionEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s. Also, for purely real x,
It is also sometimes useful to express the complex sine and cosine functions in terms of the real and imaginary parts of their arguments.
This exhibits a deep relationship between the complex sine and cosine functions and their real (sin, cos) and hyperbolic real (sinh, cosh) counterparts.
Complex graphs
In the following graphs, the domain is the complex plane pictured, and the range values are indicated at each point by color. Brightness indicates the size (absolute value) of the range value, with black being zero. Hue varies with argument, or angle, measured from the positive real axis. (more)
Trigonometric functions in the complex plane 
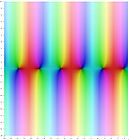
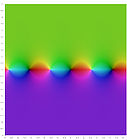


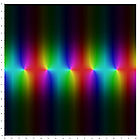






Definitions via differential equations
Both the sine and cosine functions satisfy the differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
:
That is to say, each is the additive inverse of its own second derivative. Within the 2-dimensional function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
V consisting of all solutions of this equation,- the sine function is the unique solution satisfying the initial condition
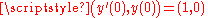 and
and - the cosine function is the unique solution satisfying the initial condition
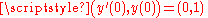 .
.
Since the sine and cosine functions are linearly independent, together they form a basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V. This method of defining the sine and cosine functions is essentially equivalent to using Euler's formula. (See linear differential equationLinear differential equationLinear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
.) It turns out that this differential equation can be used not only to define the sine and cosine functions but also to prove the trigonometric identities for the sine and cosine functions.
Further, the observation that sine and cosine satisfies y′′ = −y means that they are eigenfunctionEigenfunctionIn mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s of the second-derivative operator.
The tangent function is the unique solution of the nonlinear differential equation
satisfying the initial condition y(0) = 0. There is a very interesting visual proof that the tangent function satisfies this differential equation.
The significance of radians
Radians specify an angle by measuring the length around the path of the unit circle and constitute a special argument to the sine and cosine functions. In particular, only sines and cosines that map radians to ratios satisfy the differential equations that classically describe them. If an argument to sine or cosine in radians is scaled by frequency,
then the derivatives will scale by amplitude.
Here, k is a constant that represents a mapping between units. If x is in degrees, then
This means that the second derivative of a sine in degrees does not satisfy the differential equation
but rather
The cosine's second derivative behaves similarly.
This means that these sines and cosines are different functions, and that the fourth derivative of sine will be sine again only if the argument is in radians.
Identities
Many identities interrelate the trigonometric functions. Among the most frequently used is the Pythagorean identity, which states that for any angle, the square of the sine plus the square of the cosine is 1. This is easy to see by studying a right triangle of hypotenuse 1 and applying the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. In symbolic form, the Pythagorean identity is written

where sin2 x + cos2 x is standard notation for (sin x)2 + (cos x)2.
Other key relationships are the sum and difference formulas, which give the sine and cosine of the sum and difference of two angles in terms of sines and cosines of the angles themselves. These can be derived geometrically, using arguments that date to PtolemyPtolemyClaudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
. One can also produce them algebraically using Euler's formula.
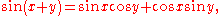


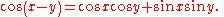
When the two angles are equal, the sum formulas reduce to simpler equations known as the double-angle formulae.
These identities can also be used to derive the product-to-sum identities that were used in antiquity to transform the product of two numbers into a sum of numbers and greatly speed operations, much like the logarithm functionLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
.
Calculus
For integralIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s and derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of trigonometric functions, see the relevant sections of Differentiation of trigonometric functionsDifferentiation of trigonometric functionsThe differentiation of trigonometric functions is the mathematical process of finding the rate at which a trigonometric function changes with respect to a variable--the derivative of the trigonometric function. Commonplace trigonometric functions include sin, cos and tan...
, Lists of integrals and List of integrals of trigonometric functions. Below is the list of the derivatives and integrals of the six basic trigonometric functions. The number C is a constant of integration.









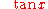


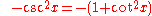



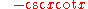
Definitions using functional equations
In mathematical analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, one can define the trigonometric functions using functional equationFunctional equationIn mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
s based on properties like the sum and difference formulas. Taking as given these formulas and the Pythagorean identity, for example, one can prove that only two real functionReal analysisReal analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
s satisfy those conditions. Symbolically, we say that there exists exactly one pair of real functions — and
and 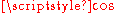 — such that for all real numbers
— such that for all real numbers  and
and  , the following equations hold:
, the following equations hold:
with the added condition that
-
 .
.
Other derivations, starting from other functional equations, are also possible, and such derivations can be extended to the complex numbers.
As an example, this derivation can be used to define trigonometry in Galois fieldsTrigonometry in Galois fieldsIn mathematics, trigonometry analogies are supported by the theory of quadratic extensions of finite fields, also known as Galois fields. The main motivation to deal with a finite field trigonometry is the power of the discrete transforms, which play an important role in engineering and mathematics...
.
Computation
The computation of trigonometric functions is a complicated subject, which can today be avoided by most people because of the widespread availability of computerComputerA computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s and scientific calculatorScientific calculatorA scientific calculator is a type of electronic calculator, usually but not always handheld, designed to calculate problems in science, engineering, and mathematics...
s that provide built-in trigonometric functions for any angle. This section, however, describes details of their computation in three important contexts: the historical use of trigonometric tables, the modern techniques used by computers, and a few "important" angles where simple exact values are easily found.
The first step in computing any trigonometric function is range reduction—reducing the given angle to a "reduced angle" inside a small range of angles, say 0 to π/2, using the periodicity and symmetries of the trigonometric functions.
Prior to computers, people typically evaluated trigonometric functions by interpolatingInterpolationIn the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
from a detailed table of their values, calculated to many significant figuresSignificant figuresThe significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except:...
. Such tables have been available for as long as trigonometric functions have been described (see History below), and were typically generated by repeated application of the half-angle and angle-addition identities starting from a known value (such as sin(π/2) = 1).
Modern computers use a variety of techniques. One common method, especially on higher-end processors with floating pointFloating pointIn computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
units, is to combine a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
or rationalRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
approximationApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
(such as Chebyshev approximationApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
, best uniform approximation, and Padé approximationPadé approximantPadé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating....
, and typically for higher or variable precisions, TaylorTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
and Laurent seriesLaurent seriesIn mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
) with range reduction and a table lookupLookup tableIn computer science, a lookup table is a data structure, usually an array or associative array, often used to replace a runtime computation with a simpler array indexing operation. The savings in terms of processing time can be significant, since retrieving a value from memory is often faster than...
—they first look up the closest angle in a small table, and then use the polynomial to compute the correction. Devices that lack hardware multipliersArithmetic logic unitIn computing, an arithmetic logic unit is a digital circuit that performs arithmetic and logical operations.The ALU is a fundamental building block of the central processing unit of a computer, and even the simplest microprocessors contain one for purposes such as maintaining timers...
often use an algorithm called CORDICCORDICCORDIC is a simple and efficient algorithm to calculate hyperbolic and trigonometric functions...
(as well as related techniques), which uses only addition, subtraction, bitshiftBitwise operationA bitwise operation operates on one or more bit patterns or binary numerals at the level of their individual bits. This is used directly at the digital hardware level as well as in microcode, machine code and certain kinds of high level languages...
, and table lookupLookup tableIn computer science, a lookup table is a data structure, usually an array or associative array, often used to replace a runtime computation with a simpler array indexing operation. The savings in terms of processing time can be significant, since retrieving a value from memory is often faster than...
. These methods are commonly implemented in hardware floating-point units for performance reasons.
For very high precision calculations, when series expansion convergence becomes too slow, trigonometric functions can be approximated by the arithmetic-geometric mean, which itself approximates the trigonometric function by the (complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
) elliptic integralElliptic integralIn integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
.
Finally, for some simple angles, the values can be easily computed by hand using the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, as in the following examples. For example, the sine, cosine and tangent of any integer multiple of radianRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
radianRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s (3°) can be found exactly by handExact trigonometric constantsExact constant expressions for trigonometric values are sometimes useful, mainly for simplifying solutions into radical forms which allow further simplification....
.
Consider a right triangle where the two other angles are equal, and therefore are both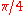 radians (45°). Then the length of side b and the length of side a are equal; we can choose
radians (45°). Then the length of side b and the length of side a are equal; we can choose  . The values of sine, cosine and tangent of an angle of
. The values of sine, cosine and tangent of an angle of 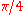 radians (45°) can then be found using the Pythagorean theorem:
radians (45°) can then be found using the Pythagorean theorem:

Therefore:
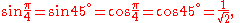

To determine the trigonometric functions for angles of π/3 radians (60 degrees) and π/6 radians (30 degrees), we start with an equilateral triangle of side length 1. All its angles are π/3 radians (60 degrees). By dividing it into two, we obtain a right triangle with π/6 radians (30 degrees) and π/3 radians (60 degrees) angles. For this triangle, the shortest side = 1/2, the next largest side =(√3)/2 and the hypotenuse = 1. This yields:



Special values in trigonometric functions
There are some commonly used special values in trigonometric functions, as shown in the following table.Function 
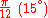

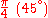


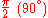
sin 
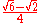

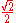

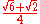
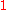
cos 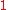

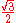


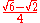

tan 


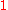



cot 


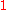



sec 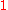





csc 

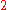

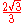

The symbol here represents the point at infinity on the real projective line, the limit on the extended real line is
here represents the point at infinity on the real projective line, the limit on the extended real line is  on one side and
on one side and  on the other.
on the other.
Inverse functions
The trigonometric functions are periodic, and hence not injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
, so strictly they do not have an inverse functionInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
. Therefore to define an inverse function we must restrict their domains so that the trigonometric function is bijectiveBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
. In the following, the functions on the left are defined by the equation on the right; these are not proved identities. The principal inverses are usually defined as:
Function Definition Value Field 

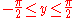

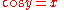

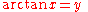
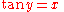

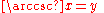
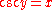


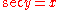

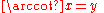
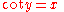
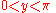
The notations sin−1 and cos−1 are often used for arcsin and arccos, etc. When this notation is used, the inverse functions could be confused with the multiplicative inverses of the functions. The notation using the "arc-" prefix avoids such confusion, though "arcsec" can be confused with "arcsecondMinute of arcA minute of arc, arcminute, or minute of angle , is a unit of angular measurement equal to one sixtieth of one degree. In turn, a second of arc or arcsecond is one sixtieth of one minute of arc....
".
Just like the sine and cosine, the inverse trigonometric functions can also be defined in terms of infinite series. For example,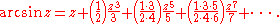
These functions may also be defined by proving that they are antiderivatives of other functions. The arcsine, for example, can be written as the following integral:

Analogous formulas for the other functions can be found at Inverse trigonometric functions. Using the complex logarithmComplex logarithmIn complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
, one can generalize all these functions to complex arguments:

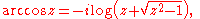

Properties and applications
The trigonometric functions, as the name suggests, are of crucial importance in trigonometryTrigonometryTrigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, mainly because of the following two results.
Law of sines
The law of sinesLaw of sinesIn trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
states that for an arbitrary triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
with sides a, b, and c and angles opposite those sides A, B and C:

or, equivalently,
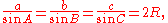
where R is the triangle's circumradiusCircumscribed circleIn geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
.
It can be proven by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in triangulation TriangulationIn trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
TriangulationIn trigonometry and geometry, triangulation is the process of determining the location of a point by measuring angles to it from known points at either end of a fixed baseline, rather than measuring distances to the point directly...
, a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
Law of cosines
The law of cosinesLaw of cosinesIn trigonometry, the law of cosines relates the lengths of the sides of a plane triangle to the cosine of one of its angles. Using notation as in Fig...
(also known as the cosine formula) is an extension of the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
:

or equivalently,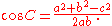
In this formula the angle at C is opposite to the side c. This theorem can be proven by dividing the triangle into two right ones and using the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.
The law of cosines can be used to determine a side of a triangle if two sides and the angle between them are known. It can also be used to find the cosines of an angle (and consequently the angles themselves) if the lengths of all the sides are known.
Law of tangents
The following all form the law of tangentsLaw of tangentsIn trigonometry, the law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposite sides....
The explanation of the formulae in words would be cumbersome, but the patterns of sums and differences; for the lengths and corresponding opposite angles, are apparent in the theorem.
Law of cotangents
If
(the radius of the inscribed circle for the triangle) and
(the semi-perimeter for the triangle), then the following all form the law of cotangentsLaw of cotangentsIn trigonometry, the law of cotangents relates the radius of the inscribed circle of a triangle to its sides and angles.When a, b, and c are the lengths of the three sides of the triangle, and α, β, and γ are the angles opposite those three respective sides...
It follows that
In words the theorem is: the cotangent of a half-angle equals the ratio of the semi-perimeter minus the opposite side to the said angle, to the inradius for the triangle.
Periodic functions
The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe simple harmonic motion Simple harmonic motionSimple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
Simple harmonic motionSimple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
, which models many natural phenomena, such as the movement of a mass attached to a spring and, for small angles, the pendular motion of a mass hanging by a string. The sine and cosine functions are one-dimensional projections of uniform circular motionUniform circular motionIn physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends...
.
Trigonometric functions also prove to be useful in the study of general periodic functionPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s. The characteristic wave patterns of periodic functions are useful for modeling recurring phenomena such as sound or light waveWaveIn physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s.
Under rather general conditions, a periodic function ƒ(x) can be expressed as a sum of sine waves or cosine waves in a Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
. Denoting the sine or cosine basis functions by φk, the expansion of the periodic function ƒ(t) takes the form:

For example, the square waveSquare waveA square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...
can be written as the Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
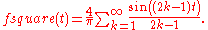
In the animation of a square wave at top right it can be seen that just a few terms already produce a fairly good approximation. The superposition of several terms in the expansion of a sawtooth waveSawtooth waveThe sawtooth wave is a kind of non-sinusoidal waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw....
are shown underneath.
History
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period.
The chordChord (geometry)A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
function was discovered by HipparchusHipparchusHipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
of NicaeaIznikİznik is a city in Turkey which is primarily known as the site of the First and Second Councils of Nicaea, the first and seventh Ecumenical councils in the early history of the Church, the Nicene Creed, and as the capital city of the Empire of Nicaea...
(180–125 BC) and PtolemyPtolemyClaudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
of Roman Egypt (90–165 AD).
The functions sine and cosine can be traced to the jyā and koti-jyāJyā, koti-jyā and utkrama-jyāJyā, koti-jyā and utkrama-jyā are three trigonometric functions introduced by Indian astronomers and mathematicians. The earliest known Indian treatise containing references to these functions is Surya Siddhanta. These are functions of arcs of circles and not functions of angles. Jyā and...
functions used in Gupta period Indian astronomy (AryabhatiyaAryabhatiyaĀryabhaṭīya or Āryabhaṭīyaṃ, a Sanskrit astronomical treatise, is the magnum opus and only extant work of the 5th century Indian mathematician, Āryabhaṭa.- Structure and style:...
, Surya SiddhantaSurya SiddhantaThe Surya Siddhanta is one of the earliest siddhanta in archeo-astronomy of the Hindus by an unknown author. It describes the archeo-astronomy theories, principles and methods of the ancient Hindus. This siddhanta is supposed to be the knowledge that the Sun god gave to an Asura called Maya. Asuras...
), via translation from Sanskrit to Arabic and then from Arabic to Latin.
All six trigonometric functions in current use were known in Islamic mathematicsIslamic mathematicsIn the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
by the 9th century, as was the law of sinesLaw of sinesIn trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
, used in solving triangles.
al-Khwārizmī produced tables of sines, cosines and tangents.
They were studied by authors including Omar KhayyámOmar KhayyámOmar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
, Bhāskara II, Nasir al-Din al-TusiNasir al-Din al-TusiKhawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
, Jamshīd al-KāshīJamshid al-KashiGhiyāth al-Dīn Jamshīd Masʾūd al-Kāshī was a Persian astronomer and mathematician.-Biography:...
(14th century), Ulugh BegUlugh BegUlugh Bek was a Timurid ruler as well as an astronomer, mathematician and sultan. His commonly-known name is not truly a personal name, but rather a moniker, which can be loosely translated as "Great Ruler" or "Patriarch Ruler" and was the Turkic equivalent of Timur's Perso-Arabic title Amīr-e...
(14th century), RegiomontanusRegiomontanusJohannes Müller von Königsberg , today best known by his Latin toponym Regiomontanus, was a German mathematician, astronomer, astrologer, translator and instrument maker....
(1464), RheticusGeorg Joachim RheticusGeorg Joachim von Lauchen, also known as Rheticus , was a mathematician, cartographer, navigational-instrument maker, medical practitioner, and teacher. He is perhaps best known for his trigonometric tables and as Nicolaus Copernicus's sole pupil...
, and Rheticus' student Valentinus OthoValentinus OthoValentinus Otho or Valentin Otto was a German mathematician and astronomer.- Life :...
Madhava of SangamagramaMadhava of SangamagramaMādhava of Sañgamāgrama was a prominent Kerala mathematician-astronomer from the town of Irińńālakkuţa near Cochin, Kerala, India. He is considered the founder of the Kerala School of Astronomy and Mathematics...
(c. 1400) made early strides in the analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
of trigonometric functions in terms of infinite seriesSeries (mathematics)A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
.
The first published use of the abbreviations 'sin', 'cos', and 'tan' is by the 16th century French mathematician Albert GirardAlbert GirardAlbert Girard was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and gave the inductive definition for the Fibonacci numbers....
.
In a paper published in 1682, LeibnizGottfried LeibnizGottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
proved that sin x is not an algebraic functionAlgebraic functionIn mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
of x.
Leonhard EulerLeonhard EulerLeonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
's Introductio in analysin infinitorum (1748) was mostly responsible for establishing the analytic treatment of trigonometric functions in Europe, also defining them as infinite series and presenting "Euler's formulaEuler's formulaEuler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
", as well as the near-modern abbreviations sin., cos., tang., cot., sec., and cosec.
A few functions were common historically, but are now seldom used, such as the chordChord (geometry)A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
(crd(θ) = 2 sin(θ/2)), the versineVersineThe versine or versed sine, versin, is a trigonometric function equal to and 2sin2. It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used...
(versin(θ) = 1 − cos(θ) = 2 sin2(θ/2)) (which appeared in the earliest tables ), the haversineVersineThe versine or versed sine, versin, is a trigonometric function equal to and 2sin2. It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used...
(haversin(θ) = versin(θ) / 2 = sin2(θ/2)), the exsecant (exsec(θ) = sec(θ) − 1) and the excosecant (excsc(θ) = exsec(π/2 − θ) = csc(θ) − 1). Many more relations between these functions are listed in the article about trigonometric identities.
EtymologicallyEtymologyEtymology is the study of the history of words, their origins, and how their form and meaning have changed over time.For languages with a long written history, etymologists make use of texts in these languages and texts about the languages to gather knowledge about how words were used during...
, the word sine derives from the SanskritSanskritSanskrit , is a historical Indo-Aryan language and the primary liturgical language of Hinduism, Jainism and Buddhism.Buddhism: besides Pali, see Buddhist Hybrid Sanskrit Today, it is listed as one of the 22 scheduled languages of India and is an official language of the state of Uttarakhand...
word for half the chord, jya-ardha, abbreviated to jiva. This was transliteratedTransliterationTransliteration is a subset of the science of hermeneutics. It is a form of translation, and is the practice of converting a text from one script into another...
in ArabicArabic languageArabic is a name applied to the descendants of the Classical Arabic language of the 6th century AD, used most prominently in the Quran, the Islamic Holy Book...
as jiba, written jb, vowels not being written in Arabic. Next, this transliteration was mis-translated in the 12th century into LatinLatinLatin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
as sinus, under the mistaken impression that jb stood for the word jaib, which means "bosom" or "bay" or "fold" in Arabic, as does sinus in Latin. Finally, English usage converted the Latin word sinus to sine. The word tangent comes from Latin tangens meaning "touching", since the line touches the circle of unit radius, whereas secant stems from Latin secans — "cutting" — since the line cuts the circle.
External links
- Visionlearning Module on Wave Mathematics
- GonioLab: Visualization of the unit circle, trigonometric and hyperbolic functions
- Dave's draggable diagram. (Requires java browser plugin)
-
-
-
-
-