Rotation around a fixed axis
Encyclopedia
Rotation around a fixed axis is a special case of rotation
al motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling
or precession
. According to Euler's rotation theorem
, simultaneous rotation around more than one axis at the same time is impossible. If two rotations are forced at the same time, a new axis of rotation will appear.
The kinematics
and dynamics
of rotation around a fixed axis of a rigid body are mathematically much simpler than those for free rotation of a rigid body; they are entirely analogous to those of linear motion
along a single fixed direction, which is not true for free rotation of a rigid body. The expressions for the kinetic energy
of the object, and for the forces on the parts of the object, are also simpler for rotation around a fixed axis, than for general rotational motion. For these reasons, rotation around a fixed axis is typically taught in introductory physics courses after students have mastered linear motion; the full generality of rotational motion is not usually taught in introductory physics classes.
. Having moved an arc length 
, its angular position is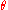 
relative to its original position, where 
.
In mathematics and physics it is usual to use the natural unit radians rather than degrees or revolutions
. Units are converted as follows:
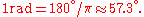
An angular displacement is a change in angular position:
where
is the angular displacement,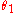 
is the initial angular position and 
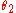is the final angular position.
and the units are typically rad s-1. Angular speed is the magnitude of angular velocity.
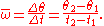
The instantaneous angular velocity is given by
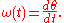
Using the formula for angular position and letting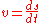
, we have also
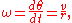
where
is the translational speed of the particle.
Angular velocity and frequency
are related by
.
over a time interval Δt is given by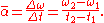
The instantaneous acceleration α(t) is given by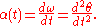
Thus, the angular acceleration is the rate of change of the angular velocity, just as acceleration is the rate of change of velocity.
The translational acceleration of a point on the object rotating is given by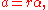
where r is the radius or distance from the axis of rotation. This is also the tangential component of acceleration: it is tangential to the direction of motion of the point. If this component is 0, the motion is uniform circular motion
, and the velocity changes in direction only.
The radial acceleration (perpendicular to direction of motion) is given by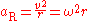
.
It is directed towards the center of the rotational motion, and is often called the centripetal acceleration.
The angular acceleration is caused by the torque
, which can have a positive or negative value in accordance with the convention of positive and negative angular frequency. The ratio of torque and angular acceleration (how difficult it is to start, stop, or otherwise change rotation) is given by the moment of inertia
:
.
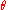, initial angular velocity 
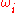, final angular velocity 
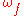, angular acceleration 
, and time 
can be related by four equations of kinematics:
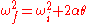
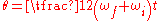
a distance 
from the axis of rotation, the moment of inertia is given by
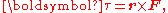
where × denotes the cross product
. A net torque acting upon an object will produce an angular acceleration of the object according to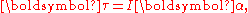
just as F = ma in linear dynamics.
The work done by a torque acting on an object equals the magnitude of the torque times the angle through which the torque is applied: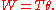
The power of a torque is equal to the work done by the torque per unit time, hence: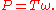
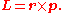
Angular momentum is related to angular velocity by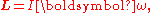
just as p = mv in linear dynamics.
Torque and angular momentum are related according to
just as F = dp/dt in linear dynamics. In the absence of an external torque, the angular momentum of a body remains constant. The conservation of angular momentum is notably demonstrated in figure skating
: when pulling the arms closer to the body during a spin, the moment of inertia is decreased, and so the angular velocity is increased.
just as Ktrans = mv2 in linear dynamics.
An angular displacement is considered to be a vector, pointing along the axis, of magnitude equal to that of
. A right-hand rule
is used to find which way it points along the axis; if the fingers of the right hand are curled to point in the way that the object has rotated, then the thumb of the right hand points in the direction of the vector.
The angular velocity
vector also points along the axis of rotation in the same way as the angular displacements it causes. If a disk spins counterclockwise as seen from above, its angular velocity vector points upwards. Similarly, the angular acceleration
vector points along the axis of rotation in the same direction that the angular velocity would point if the angular acceleration were maintained for a long time.
The torque vector points along the axis around which the torque tends to cause rotation. To maintain rotation around a fixed axis, the total torque vector has to be along the axis, so that it only changes the magnitude and not the direction of the angular velocity vector. In the case of a hinge, only the component of the torque vector along the axis has effect on the rotation, other forces and torques are compensated by the structure.
, the motor applies a torque to compensate for friction. The angle of rotation is a linear function of time, which modulo 360° is a periodic function.
An example of this is the two-body problem
with circular orbit
s.
that keeps a spinning object together. A rigid body
model neglects the accompanying strain
. If the body is not rigid this strain will cause it to change shape. This is expressed as the object changing shape due to the "centrifugal force
".
Celestial bodies rotating about each other often have elliptic orbit
s. The special case of circular orbit
s is an example of a rotation around a fixed axis: this axis is the line through the center of mass
perpendicular to the plane of motion. The centripetal force is provided by gravity, see also two-body problem
. This usually also applies for a spinning celestial body, so it need not be solid to keep together, unless the angular speed is too high in relation to its density. (It will, however, tend to become oblate.) For example, a spinning celestial body of water must take at least 3 hours and 18 minutes to rotate, regardless of size, or the water will separate. If the density of the fluid is higher the time can be less. See orbital period
.
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
al motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling
Nutation
Nutation is a rocking, swaying, or nodding motion in the axis of rotation of a largely axially symmetric object, such as a gyroscope, planet, or bullet in flight, or as an intended behavior of a mechanism...
or precession
Precession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
. According to Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
, simultaneous rotation around more than one axis at the same time is impossible. If two rotations are forced at the same time, a new axis of rotation will appear.
The kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
and dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
of rotation around a fixed axis of a rigid body are mathematically much simpler than those for free rotation of a rigid body; they are entirely analogous to those of linear motion
Linear motion
Linear motion is motion along a straight line, and can therefore be described mathematically using only one spatial dimension. The linear motion can be of two types: uniform linear motion, with constant velocity or zero acceleration; non uniform linear motion, with variable velocity or non-zero...
along a single fixed direction, which is not true for free rotation of a rigid body. The expressions for the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the object, and for the forces on the parts of the object, are also simpler for rotation around a fixed axis, than for general rotational motion. For these reasons, rotation around a fixed axis is typically taught in introductory physics courses after students have mastered linear motion; the full generality of rotational motion is not usually taught in introductory physics classes.
Angular Displacement
A particle moves in a circle of radius. Having moved an arc length , its angular position is 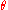relative to its original position, where .In mathematics and physics it is usual to use the natural unit radians rather than degrees or revolutions
Revolutions per minute
Revolutions per minute is a measure of the frequency of a rotation. It annotates the number of full rotations completed in one minute around a fixed axis...
. Units are converted as follows:
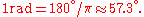
An angular displacement is a change in angular position:
where
is the angular displacement, 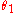is the initial angular position and 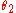is the final angular position.Angular speed and angular velocity
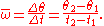
Angular velocity is the change in angular displacement per unit time. The symbol for angular velocity is and the units are typically rad s-1. Angular speed is the magnitude of angular velocity.The instantaneous angular velocity is given by
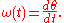
Using the formula for angular position and letting
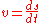, we have also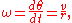where
is the translational speed of the particle.Angular velocity and frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
are related by
.Angular acceleration
A changing angular velocity indicates the presence of an angular acceleration in rigid body, typically measured in rad s−2. The average angular acceleration over a time interval Δt is given by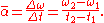The instantaneous acceleration α(t) is given by
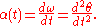
Thus, the angular acceleration is the rate of change of the angular velocity, just as acceleration is the rate of change of velocity.
The translational acceleration of a point on the object rotating is given by
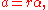
where r is the radius or distance from the axis of rotation. This is also the tangential component of acceleration: it is tangential to the direction of motion of the point. If this component is 0, the motion is uniform circular motion
Uniform circular motion
In physics, uniform circular motion describes the motion of a body traversing a circular path at constant speed. The distance of the body from the axis of rotation remains constant at all times. Though the body's speed is constant, its velocity is not constant: velocity, a vector quantity, depends...
, and the velocity changes in direction only.
The radial acceleration (perpendicular to direction of motion) is given by
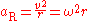.It is directed towards the center of the rotational motion, and is often called the centripetal acceleration.
The angular acceleration is caused by the torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
, which can have a positive or negative value in accordance with the convention of positive and negative angular frequency. The ratio of torque and angular acceleration (how difficult it is to start, stop, or otherwise change rotation) is given by the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
:
.Equations of kinematics
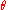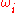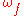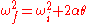
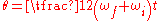
When the angular acceleration is constant, the five quantities angular displacement, initial angular velocity , final angular velocity , angular acceleration , and time can be related by four equations of kinematics:Moment of inertia
The moment of inertia of an object, symbolized by I or J, is a measure of the object's resistance to changes to its rotation. The moment of inertia is measured in kilogram metre² (kg m²). It depends on the objects mass: increasing the mass of an object increases the moment of inertia. It also depends on the distribution of the mass: distributing the mass further from the centre of rotation increases the moment of inertia by a greater degree. For a single particle of mass a distance from the axis of rotation, the moment of inertia is given byTorque
Torque τ is the twisting effect of a force F applied to a rotating object which is at position r from its axis of rotation. Mathematically,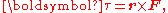where × denotes the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
. A net torque acting upon an object will produce an angular acceleration of the object according to
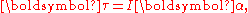
just as F = ma in linear dynamics.
The work done by a torque acting on an object equals the magnitude of the torque times the angle through which the torque is applied:
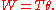
The power of a torque is equal to the work done by the torque per unit time, hence:
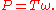
Angular Momentum
The angular momentum L is a measure of the difficulty of bringing a rotating object to rest. It is given by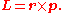Angular momentum is related to angular velocity by
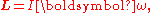
just as p = mv in linear dynamics.
Torque and angular momentum are related according to
just as F = dp/dt in linear dynamics. In the absence of an external torque, the angular momentum of a body remains constant. The conservation of angular momentum is notably demonstrated in figure skating
Figure skating
Figure skating is an Olympic sport in which individuals, pairs, or groups perform spins, jumps, footwork and other intricate and challenging moves on ice skates. Figure skaters compete at various levels from beginner up to the Olympic level , and at local, national, and international competitions...
: when pulling the arms closer to the body during a spin, the moment of inertia is decreased, and so the angular velocity is increased.
Kinetic energy
The kinetic energy Krot due to the rotation of the body is given byjust as Ktrans = mv2 in linear dynamics.
Vector expression
The above development is a special case of general rotational motion. In the general case, angular displacement, angular velocity, angular acceleration and torque are considered to be vectors.An angular displacement is considered to be a vector, pointing along the axis, of magnitude equal to that of
. A right-hand ruleRight-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
is used to find which way it points along the axis; if the fingers of the right hand are curled to point in the way that the object has rotated, then the thumb of the right hand points in the direction of the vector.
The angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector also points along the axis of rotation in the same way as the angular displacements it causes. If a disk spins counterclockwise as seen from above, its angular velocity vector points upwards. Similarly, the angular acceleration
Angular acceleration
Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...
vector points along the axis of rotation in the same direction that the angular velocity would point if the angular acceleration were maintained for a long time.
The torque vector points along the axis around which the torque tends to cause rotation. To maintain rotation around a fixed axis, the total torque vector has to be along the axis, so that it only changes the magnitude and not the direction of the angular velocity vector. In the case of a hinge, only the component of the torque vector along the axis has effect on the rotation, other forces and torques are compensated by the structure.
Constant angular speed
The simplest case of rotation around a fixed axis is that of constant angular speed. Then the total torque is zero. For the example of the Earth rotating around its axis, there is very little friction. For a fanFan (mechanical)
A mechanical fan is a machine used to create flow within a fluid, typically a gas such as air.A fan consists of a rotating arrangement of vanes or blades which act on the air. Usually, it is contained within some form of housing or case. This may direct the airflow or increase safety by preventing...
, the motor applies a torque to compensate for friction. The angle of rotation is a linear function of time, which modulo 360° is a periodic function.
An example of this is the two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
with circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
s.
Centripetal force
Internal tensile stress provides the centripetal forceCentripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
that keeps a spinning object together. A rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
model neglects the accompanying strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
. If the body is not rigid this strain will cause it to change shape. This is expressed as the object changing shape due to the "centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
".
Celestial bodies rotating about each other often have elliptic orbit
Elliptic orbit
In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
s. The special case of circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
s is an example of a rotation around a fixed axis: this axis is the line through the center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
perpendicular to the plane of motion. The centripetal force is provided by gravity, see also two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
. This usually also applies for a spinning celestial body, so it need not be solid to keep together, unless the angular speed is too high in relation to its density. (It will, however, tend to become oblate.) For example, a spinning celestial body of water must take at least 3 hours and 18 minutes to rotate, regardless of size, or the water will separate. If the density of the fluid is higher the time can be less. See orbital period
Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
.