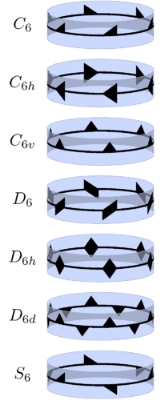
Point groups in three dimensions - AbsoluteAstronomy.com

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...

in three dimensions is an isometry group

Isometry group

In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...

in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

. It is a subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

of the orthogonal group

Orthogonal group

In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...

O(3), the group of all isometries

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

that leave the origin fixed, or correspondingly, the group of orthogonal matrices

Orthogonal matrix

In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....

. O(3) itself is a subgroup of the Euclidean group

Euclidean group

In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...

E(3) of all isometries.

Symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

s of objects are isometry groups. Accordingly, analysis of isometry groups is analysis of possible symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

. All isometries of a bounded 3D object have one or more common fixed points. We choose the origin as one of them.

The symmetry group of an object is sometimes also called full symmetry group, as opposed to its rotation group or proper symmetry group, the intersection of its full symmetry group and the rotation group SO(3)

Rotation group

In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...

of the 3D space itself. The rotation group of an object is equal to its full symmetry group if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

the object is chiral

Chirality (mathematics)

In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...

.

The point groups in three dimensions are heavily used in chemistry, especially to describe the symmetries of a molecule

Molecule

A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...

and of molecular orbital

Molecular orbital

In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...

s forming covalent bond

Covalent bond

A covalent bond is a form of chemical bonding that is characterized by the sharing of pairs of electrons between atoms. The stable balance of attractive and repulsive forces between atoms when they share electrons is known as covalent bonding....

s, and in this context they are also called molecular point groups.

Group structure

SO(3) is a subgroup of E⁺(3), which consists of direct isometries, i.e., isometries preserving orientation

Orientation (mathematics)

In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...

; it contains those that leave the origin fixed.

O(3) is the direct product

Direct product of groups

In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...

of SO(3) and the group generated by inversion (denoted by its matrix −I):

O(3) = SO(3) × { I , −I }

Thus there is a 1-to-1 correspondence between all direct isometries and all indirect isometries, through inversion. Also there is a 1-to-1 correspondence between all groups of direct isometries H and all groups K of isometries that contain inversion:

K = H × { I , −I }

H = K ∩ SO(3)

If a group of direct isometries H has a subgroup L of index

Index of a subgroup

In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...

2, then, apart from the corresponding group containing inversion there is also a corresponding group that contains indirect isometries but no inversion:

M = L ∪ ( (H \ L) × { − I } )

where isometry ( A , I ) is identified with A.

Thus M is obtained from H by inverting the isometries in H \ L. This group M is as abstract group isomorphic with H. Conversely, for all isometry groups that contain indirect isometries but no inversion we can obtain a rotation group by inverting the indirect isometries. This is clarifying when categorizing isometry groups, see below.

In 2D the cyclic group

Cyclic group

In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

of k-fold rotation

Rotation

A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

s C_k is for every positive integer k a normal subgroup of O(2,R) and SO(2,R). Accordingly, in 3D, for every axis the cyclic group of k-fold rotations about that axis is a normal subgroup of the group of all rotations about that axis, and also of the group obtained by adding reflections in planes through the axis.

3D isometries that leave origin fixed

The isometries of R³ that leave the origin fixed, forming the group O(3,R), can be categorized as follows:

SO(3,R):
- identity
- rotation about an axis through the origin by an angle not equal to 180°
- rotation about an axis through the origin by an angle of 180°
the same with inversion (x is mapped to −x), i.e. respectively:
- inversion
- rotation about an axis by an angle not equal to 180°, combined with reflection in the plane through the origin perpendicular to the axis
- reflection in a plane through the origin

The 4th and 5th in particular, and in a wider sense the 6th also, are called improper rotation

Improper rotation

In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...

s.

See also the similar overview including translations.

Conjugacy

When comparing the symmetry type of two objects, the origin is chosen for each separately, i.e. they need not have the same center. Moreover, two objects are considered to be of the same symmetry type if their symmetry groups are conjugate subgroups of O(3) (two subgroups H₁, H₂ of a group G are conjugate, if there exists g ∈ G such that H₁ = g⁻¹H₂g ).

Thus two 3D objects have the same symmetry type:

if both have mirror symmetry, but with respect to a different mirror plane
if both have 3-fold rotational symmetry, but with respect to a different axis.

In the case of multiple mirror planes and/or axes of rotation, two symmetry groups are of the same symmetry type if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

there is a single rotation mapping this whole structure of the first symmetry group to that of the second. The conjugacy definition would also allow a mirror image of the structure, but this is not needed, the structure itself is achiral. For example, if a symmetry group contains a 3-fold axis of rotation, it contains rotations in two opposite directions. (The structure is chiral for 11 pairs of space group

Space group

In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...

s with a screw axis.)

Infinite isometry groups

We restrict ourselves to isometry groups that are closed as topological subgroups

Topological group

In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...

of O(3). This excludes for example the group of rotations by an irrational number of turns about an axis.

The whole O(3) is the symmetry group of spherical symmetry; SO(3) is the corresponding rotation group

Rotation group

. The other infinite isometry groups consist of all rotation

Rotation

s about an axis through the origin, and those with additionally reflection in the planes through the axis, and/or reflection in the plane through the origin, perpendicular to the axis. Those with reflection in the planes through the axis, with or without reflection in the plane through the origin, perpendicular to the axis, are the symmetry groups for the two types of cylindrical symmetry.

See also rotational symmetry with respect to any angle.

Finite isometry groups

For point groups, being finite corresponds to being discrete

Discrete group

In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...

; infinite discrete groups as in the case of translational

Translation (geometry)

In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...

symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

and glide reflection

Glide reflection

In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...

al symmetry do not apply.

Symmetries in 3D that leave the origin fixed are fully characterized by symmetries on a sphere centered at the origin. For finite 3D point groups, see also spherical symmetry groups.

Up to conjugacy the set of finite 3D point groups consists of:

7 infinite series with at most one more-than-2-fold rotation axis; they are the finite symmetry groups on an infinite cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...

, or equivalently, those on a finite cylinder. They are sometimes called the axial or prismatic point groups.
7 point groups with multiple 3-or-more-fold rotation axes; they can also be characterized as point groups with multiple 3-fold rotation axes, because all 7 include these axes; with regard to 3-or-more-fold rotation axes the possible combinations are:
- 4×3
- 4×3 and 3×4
- 10×3 and 6×5

A selection of point groups is compatible with discrete translational symmetry

Translational symmetry

In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...

: 27 from the 7 infinite series, and 5 of the 7 others, the 32 so-called crystallographic point groups. See also the crystallographic restriction theorem

Crystallographic restriction theorem

The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...

The seven infinite series of axial groups

The infinite series of axial or prismatic groups have an index n, which can be any integer; in each series, the nth symmetry group contains n-fold rotational symmetry

Rotational symmetry

Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...

about an axis, i.e. symmetry with respect to a rotation by an angle 360°/n. n=1 covers the cases of no rotational symmetry at all. There are four series with no other axes of rotational symmetry, see cyclic symmetries
Cyclic symmetries
This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...

, and three with additional axes of 2-fold symmetry, see dihedral symmetry. They can be understood as point groups in two dimensions

Point groups in two dimensions

In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O, including O itself...

extended with an axial coordinate and reflections in it.

They are related to the frieze group

Frieze group

A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s; they can be interpreted as frieze-group patterns repeated n times around a cylinder. This table lists several notations for point groups: Hermann–Mauguin notation, Schönflies

Arthur Moritz Schönflies

Arthur Moritz Schoenflies , sometimes written as Schönflies, was a German mathematician, known for his contributions to the application of group theory to crystallography, and for work in topology....

notation, and orbifold notation. The latter is not only conveniently related to its properties, but also to the order of the group, see below. It is a unified notation, also applicable for wallpaper group

Wallpaper group

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s and frieze group

Frieze group

s. The crystallographic groups have n restricted to 1, 2, 3, 4, and 6; removing crystallographic restriction allows any positive integer.

The series are:

Hermann–Mauguin		Schönflies	Orbifold	Frieze	Order	Abstract group		Comments
Even n	Odd n	Schönflies	Orbifold	Frieze	Order	Even n	Odd n	Comments
n		C_n	nn	p1	n	Z_n		n-fold rotational symmetry
		S_2n	nx	p11g	2n	Z_2n		Not to be confused with the symmetric group Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... s
n/m		C_nh	n*	p11m	2n	Z_n × Z₂	Z_2n = Z_n × Z₂
nmm	nm	C_nv	*nn	p1m1	2n	Dih_n		Pyramidal symmetry; in biology, biradial symmetry
n22	n2	D_n	22n	p211	2n	Dih_n		Dihedral symmetry
2m	m	D_nd, D_nv	2n	p2mg	4n	Dih_2n		Antiprismatic symmetry
n/mmm	2m	D_nh	*22n	p2mm	4n	Dih_n × Z₂	Dih_2n = Dih_n × Z₂	Prismatic symmetry

The terms horizontal (h) and vertical (v), and the corresponding subscripts, refer to the additional mirror plane, that can be parallel to the rotation axis (vertical) or perpendicular to the rotation axis (horizontal).

The simplest nontrivial ones have Involutional symmetry (abstract group Z₂ ):

C_i – inversion
Inverse (mathematics)
In many contexts in mathematics the term inverse indicates the opposite of something. This word and its derivatives are used widely in mathematics, as illustrated below....

symmetry
C₂ – 2-fold rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
C_s – reflection symmetry
Reflection symmetry
Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...

, also called bilateral symmetry.

The second of these is the first of the uniaxial groups (cyclic group

Cyclic group

s) C_n of order n (also applicable in 2D), which are generated by a single rotation of angle 360°/n. In addition to this, one may add a mirror plane perpendicular to the axis, giving the group C_nh of order 2n, or a set of n mirror planes containing the axis, giving the group C_nv, also of order 2n. The latter is the symmetry group for a regular n-sided pyramid

Pyramid

A pyramid is a structure whose outer surfaces are triangular and converge at a single point. The base of a pyramid can be trilateral, quadrilateral, or any polygon shape, meaning that a pyramid has at least three triangular surfaces...

. A typical object with symmetry group C_n or D_n is a propeller

Propeller

A propeller is a type of fan that transmits power by converting rotational motion into thrust. A pressure difference is produced between the forward and rear surfaces of the airfoil-shaped blade, and a fluid is accelerated behind the blade. Propeller dynamics can be modeled by both Bernoulli's...

.

If both horizontal and vertical reflection planes are added, their intersections give n axes of rotation through 180°, so the group is no longer uniaxial. This new group of order 4n is called D_nh. Its subgroup of rotations is the dihedral group

Dihedral group

In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

D_n of order 2n, which still has the 2-fold rotation axes perpendicular to the primary rotation axis, but no mirror planes. Note that in 2D D_n includes reflections, which can also be viewed as flipping over flat objects without distinction of front- and backside, but in 3D the two operations are distinguished: the group contains "flipping over", not reflections.

There is one more group in this family, called D_nd (or D_nv), which has vertical mirror planes containing the main rotation axis, but instead of having a horizontal mirror plane, it has an isometry that combines a reflection in the horizontal plane and a rotation by an angle 180°/n. D_nh is the symmetry group for a regular n-sided prisms

Prism (geometry)

In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...

and also for a regular n-sided bipyramid

Bipyramid

An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...

. D_nd is the symmetry group for a regular n-sided antiprism

Antiprism

In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...

, and also for a regular n-sided trapezohedron

Trapezohedron

The n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry...

. D_n is the symmetry group of a partially rotated prism.

S_n is generated by the combination of a reflection in the horizontal plane and a rotation by an angle 360°/n. For n odd this is equal to the group generated by the two separately, C_nh of order 2n, and therefore the notation S_n is not needed; however, for n even it is distinct, and of order n. Like D_nd it contains a number of improper rotation

Improper rotation

s without containing the corresponding rotations.

All symmetry groups in the 7 infinite series are different, except for the following four pairs of mutually equal ones:

C_1h and C_1v: group of order 2 with a single reflection (C_s )
D₁ and C₂: group of order 2 with a single 180° rotation
D_1h and C_2v: group of order 4 with a reflection in a plane and a 180° rotation through a line in that plane
D_1d and C_2h: group of order 4 with a reflection in a plane and a 180° rotation through a line perpendicular to that plane

S₂ is the group of order 2 with a single inversion (C_i )

"Equal" is meant here as the same up to conjugacy in space. This is stronger than "up to algebraic isomorphism". For example, there are three different groups of order two in the first sense, but there is only one in the second sense. Similarly, e.g. S_2n is algebraically isomorphic with Z_2n.

The groups may be constructed as follows:

C_n. Generated by an element also called C_n, which corresponds to a rotation by angle 2π/n around the axis. Its elements are E (the identity), C_n, C_n², ..., C_nⁿ⁻¹, corresponding to rotation angles 0, 2π/n, 4π/n, ..., 2(n − 1)π/n.
S_2n. Generated by elements C_2nσ_h, where σ_h is a reflection in the direction of the axis. Its elements are the elements of C_n with C_2nσ_h, C_2n³σ_h, ..., C_2n²ⁿ⁻¹σ_h added.
C_nh. Generated by element C_n and reflection σ_h. Its elements are the elements of group C_n, with elements σ_h, C_nσ_h, C_n²σ_h, ..., C_nⁿ⁻¹σ_h added.
C_nv. Generated by element C_n and reflection σ_v in a direction in the plane perpendicular to the axis. Its elements are the elements of group C_n, with elements σ_v, C_nσ_v, C_n²σ_v, ..., C_nⁿ⁻¹σ_v added.
D_n. Generated by element C_n and 180° rotation U = σ_hσ_v around a direction in the plane perpendicular to the axis. Its elements are the elements of group C_n, with elements U, C_nU, C_n²U, ..., C_n^n − 1U added.
D_nd. Generated by elements C_2nσ_h and σ_v. Its elements are the elements of group C_n and the additional elements of S_2n and C_nv, with elements C_2nσ_hσ_v, C_2n³σ_hσ_v, ..., C_2n^2n − 1σ_hσ_v added.
D_nh. Generated by elements C_n, σ_h, and σ_v. Its elements are the elements of group C_n and the additional elements of C_nh, C_nv, and D_n.

Taking n to ∞ yields groups with continuous axial rotations:

H–M	Schönflies	Limit of	Abstract group
∞	C_∞	C_n	SO(2)
, ∞/m	C_∞h	C_nh, S_2n	SO(2) × Z₂
∞m	C_∞v	C_nv	O(2)
∞2	D_∞	D_n	O(2)
m, ∞/mm	D_∞h	D_nh, D_nd	O(2) × Z₂

The seven remaining point groups

The remaining point groups are said to be of very high or polyhedral

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

symmetry because they have more than one rotation axis of order greater than 2. Here, C_n denotes an axis of rotation through 360°/n and S_n denotes an axis of improper rotation through the same. In parentheses are the orbifold notation, the full Hermann–Mauguin notation, and the abbreviated one if different. The groups are:

T (332, 23) of order 12 – chiral tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...

. There are four C₃ axes, each through two vertices of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...

(body diagonals) or one of a regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

, and three C₂ axes, through the centers of the cube's faces, or the midpoints of the tetrahedron's edges. This group is isomorphic to A₄, the alternating group on 4 elements, and is the rotation group for a regular tetrahedron.

T_d (*332, 3m) of order 24 – full tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...

. This group has the same rotation axes as T, but with six mirror planes, each containing two edges of the cube or one edge of the tetrahedron, a single C₂ axis and two C₃ axes. The C₂ axes are now actually S₄ axes. This group is the symmetry group for a regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

. T_d is isomorphic to S₄, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...

on 4 letters. See also the isometries of the regular tetrahedron.

T_h (3*2, 2/m, m) of order 24 – pyritohedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...

.
This group has the same rotation axes as T, with mirror planes parallel to the cube faces. The C₃ axes become S₆ axes, and there is inversion symmetry. T_h is isomorphic to A₄ × C₂. It is the symmetry of a cube with on each face a line segment dividing the face into two equal rectangles, such that the line segments of adjacent faces do not meet at the edge. The symmetries correspond to the even permutations of the body diagonals and the same combined with inversion. It is also the symmetry of a pyritohedron
Pyritohedron
In geometry, a pyritohedron is an irregular dodecahedron with pyritohedral symmetry. Like the regular dodecahedron, it has twelve identical pentagonal faces, with three meeting in each of the 20 vertices. However, the pentagons are not regular, and the structure has no fivefold symmetry axes...

, which is similar to the cube described, with each rectangle replaced by a pentagon with one symmetry axis and 4 equal sides and 1 different side (the one corresponding to the line segment dividing the cube's face); i.e., the cube's faces bulge out at the dividing line and become narrower there. It is a subgroup of the full icosahedral symmetry group (as isometry group, not just as abstract group), with 4 of the 10 3-fold axes.

O (432, 432) of order 24 – chiral octahedral symmetry
Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...

. This group is like T, but the C₂ axes are now C₄ axes, and additionally there are 6 C₂ axes, through the midpoints of the edges of the cube. This group is also isomorphic to S₄, and is the rotation group of the cube and octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

.

O_h (*432, 4/m2/m, mm) of order 48 – full octahedral symmetry. This group has the same rotation axes as O, but with mirror planes, comprising both the mirror planes of T_d and T_h. This group is isomorphic to S₄ × C₂, and is the symmetry group of the cube and octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

. See also the isometries of the cube.

I (532, 532) of order 60 – chiral icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...

; the rotation group of the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

and the dodecahedron. It is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....

of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...

2 in the full group of symmetries I_h. The group I is isomorphic to A₅, the alternating group on 5 letters. The group contains 10 versions of D₃ and 6 versions of D₅ (rotational symmetries like prisms and antiprisms).

I_h (*532, 2/m, m) of order 120 – full icosahedral symmetry; the symmetry group of the icosahedron and the dodecahedron. The group I_h is isomorphic to A₅ × C₂. The group contains 10 versions of D_3d and 6 versions of D_5d (symmetries like antiprisms).

The continuous groups related to these groups are:

K or SO(3), all possible rotations.
K_h or O(3), all possible rotations and reflections.

Relation between orbifold notation and order

The order of each group is 2 divided by the orbifold

Orbifold

In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

; the latter is 2 minus the sum of the feature values, assigned as follows:

n without or before * counts as (n−1)/n
n after * counts as (n−1)/(2n)
* and x count as 1

This can also be applied for wallpaper group

Wallpaper group

s and frieze group

Frieze group

s: for them, the sum of the feature values is 2, giving an infinite order; see orbifold Euler characteristic for wallpaper groups

Rotation groups

The rotation groups, i.e. the finite subgroups of SO(3), are: the cyclic groups C_n (the rotation group of a regular pyramid

Pyramid

), the dihedral groups D_n (the rotation group of a regular prism

Prism (geometry)

, or regular bipyramid

Bipyramid

), and the rotation groups T, O and I of a regular tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

, octahedron

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

/cube

Cube

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...

and icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

/dodecahedron.

In particular, the dihedral groups D₃, D₄ etc. are the rotation groups of plane regular polygons embedded in three-dimensional space, and such a figure may be considered as a degenerate regular prism. Therefore it is also called a dihedron (Greek: solid with two faces), which explains the name dihedral group.

An object with symmetry group C_n, C_nh, C_nv or S_2n has rotation group C_n.

An object with symmetry group D_n, D_nh, or D_nd has rotation group D_n.
An object with one of the other seven symmetry groups has as rotation group the corresponding one without subscript: T, O or I.

The rotation group of an object is equal to its full symmetry group if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

the object is chiral

Chirality (mathematics)

. In other words, the chiral objects are those with their symmetry group in the list of rotation groups.

Correspondence between rotation groups and other groups

The following groups contain inversion:

C_nh and D_nh for even n
S_2n and D_nd for odd n (S₂ = C_i is the group generated by inversion; D_1d = C_2h)
T_h, O_h, and I_h

As explained above, there is a 1-to-1 correspondence between these groups and all rotation groups:

C_nh for even n and S_2n for odd n correspond to C_n
D_nh for even n and D_nd for odd n correspond to D_n
T_h, O_h, and I_h correspond to T, O, and I, respectively.

The other groups contain indirect isometries, but not inversion:

C_nv
C_nh and D_nh for odd n
S_2n and D_nd for even n
T_d

They all correspond to a rotation group H and a subgroup L of index 2 in the sense that they are obtained from H by inverting the isometries in H \ L, as explained above:

C_n is subgroup of D_n of index 2, giving C_nv
C_n is subgroup of C_2n of index 2, giving C_nh for odd n and S_2n for even n
D_n is subgroup of D_2n of index 2, giving D_nh for odd n and D_nd for even n
T is subgroup of O of index 2, giving T_d

Maximal symmetries

There are two discrete point groups with the property that no discrete point group has it as proper subgroup: O_h and I_h. Their largest common subgroup is T_h. The two groups are obtained from it by changing 2-fold rotational symmetry to 4-fold, and adding 5-fold symmetry, respectively. Alternatively the two groups are generated by adding for each a reflection plane to T_h.

There are two crystallographic point groups with the property that no crystallographic point group has it as proper subgroup: O_h and D_6h. Their maximal common subgroups, depending on orientation, are D_3d and D_2h.

The groups arranged by abstract group type

Below the groups explained above are arranged by abstract group type.

The smallest abstract groups that are not any symmetry group in 3D, are the quaternion group

Quaternion group

In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...

(of order 8), the dicyclic group Dic₃ (of order 12), and 10 of the 14 groups of order 16.

The column "# of order 2 elements" in the following tables shows the total number of isometry subgroups of types C₂ , C_i , C_s. This total number is one of the characteristics helping to distinguish the various abstract group types, while their isometry type helps to distinguish the various isometry groups of the same abstract group.

Within the possibilities of isometry groups in 3D, there are infinitely many abstract group types with 0, 1 and 3 elements of order 2, there are two with 2n + 1 elements of order 2, and there are three with 2n + 3 elements of order 2 (for each n ≥ 2 ). There is never a positive even number of elements of order 2.

Symmetry groups in 3D that are cyclic as abstract group

The symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

for n-fold rotational symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

is C_n; its abstract group type is cyclic group

Cyclic group

Z_n , which is also denoted by C_n. However, there are two more infinite series of symmetry groups with this abstract group type:

For even order 2n there is the group S_2n
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...

(Schoenflies notation) generated by a rotation by an angle 180°/n about an axis, combined with a reflection in the plane perpendicular to the axis. For S₂ the notation C_i is used; it is generated by inversion.
For any order 2n where n is odd, we have C_nh; it has an n-fold rotation axis, and a perpendicular plane of reflection. It is generated by a rotation by an angle 360°/n about the axis, combined with the reflection. For C_1h the notation C_s is used; it is generated by reflection in a plane.

Thus we have, with bolding of the 10 cyclic crystallographic point groups, for which the crystallographic restriction

Crystallographic restriction theorem

The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...

applies:

Order	Isometry groups	Abstract group	# of order 2 elements
1	C₁	Z₁	0
2	C₂ , *C_i* , *C_s*	Z₂	1
3	C₃	Z₃	0
4	C₄ , S₄	Z₄	1
5	C₅	Z₅	0
6	C₆ , S₆ , *C_3h*	Z₆ = Z₃ × Z₂	1
7	C₇	Z₇	0
8	C₈ , S₈	Z₈	1
9	C₉	Z₉	0
10	C₁₀ , S₁₀ , C_5h	Z₁₀ = Z₅ × Z₂	1

etc.

Symmetry groups in 3D that are dihedral as abstract group

In 2D dihedral group

Dihedral group

D_n includes reflections, which can also be viewed as flipping over flat objects without distinction of front- and backside.

However, in 3D the two operations are distinguished: the symmetry group denoted by D_n contains n 2-fold axes perpendicular to the n-fold axis, not reflections. D_n is the rotation group

Rotation group

of the n-sided prism

Prism (geometry)

with regular base, and n-sided bipyramid

Bipyramid

with regular base, and also of a regular, n-sided antiprism

Antiprism

In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...

and of a regular, n-sided trapezohedron

Trapezohedron

. The group is also the full symmetry group of such objects after making them chiral

Chirality (mathematics)

by e.g. an identical chiral marking on every face, or some modification in the shape.

The abstract group type is dihedral group

Dihedral group

Dih_n, which is also denoted by D_n. However, there are three more infinite series of symmetry groups with this abstract group type:

C_nv of order 2n, the symmetry group of a regular n-sided pyramid
Pyramid
A pyramid is a structure whose outer surfaces are triangular and converge at a single point. The base of a pyramid can be trilateral, quadrilateral, or any polygon shape, meaning that a pyramid has at least three triangular surfaces...
D_nd of order 4n, the symmetry group of a regular n-sided antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
D_nh of order 4n for odd n. For n = 1 we get D₂, already covered above, so n ≥ 3.

Note the following property:

Dih_4n+2

Dih_2n+1 × Z₂

Thus we have, with bolding of the 12 crystallographic point groups, and writing D_1d as the equivalent C_2h:

Order	Isometry groups	Abstract group	# of order 2 elements
4	D₂ , *C_2v* , *C_2h*	Dih₂ = Z₂ × Z₂	3
6	D₃ , *C_3v*	Dih₃	3
8	D₄ , *C_4v* , *D_2d*	Dih₄	5
10	D₅ , C_5v	Dih₅	5
12	D₆ , *C_6v* , *D_3d* , *D_3h*	Dih₆ = Dih₃ × Z₂	7
14	D₇ , C_7v	Dih₇	7
16	D₈ , C_8v , D_4d	Dih₈	9
18	D₉ , C_9v	Dih₉	9
D₁₀ , C_10v , D_5h , D_5d	Dih₁₀ = D₅ × Z₂	11

etc.

Other

C_2n,h of order 4n is of abstract group type Z_2n × Z₂. For n = 1 we get Dih₂ , already covered above, so n ≥ 2.

Thus we have, with bolding of the 2 cyclic crystallographic point groups:

Order	Isometry group	Abstract group	# of order 2 elements
8	*C_4h*	Z₄ × Z₂	3
12	*C_6h*	Z₆ × Z₂ = Z₃ × Z₂ × Z₂ = Z₃ × Dih₂	3
16	C_8h	Z₈ × Z₂	3
20	C_10h	Z₁₀ × Z₂ = Z₅ × Z₂ × Z₂	3

etc.

D_nh of order 4n is of abstract group type Dih_n × Z₂. For odd n this is already covered above, so we have here D_2nh of order 8n, which is of abstract group type Dih_2n × Z₂ (n≥1).

Thus we have, with bolding of the 3 dihedral crystallographic point groups:

Order	Isometry group	Abstract group	# of order 2 elements
8	*D_2h*	Dih₂ × Z₂	7
16	*D_4h*	Dih₄ × Z₂	11
24	*D_6h*	Dih₆ × Z₂	15
32	D_8h	Dih₈ × Z₂	19

etc.

The remaining seven are, with bolding of the 5 crystallographic point groups (see also above):

order 12: of type A₄ (alternating group): T
order 24:
- of type S₄ (symmetric group
  Symmetric group
  In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
  
  , not to be confused with the symmetry group with this notation): T_d, O
- of type A₄ × Z₂: T_h .
order 48, of type S₄ × Z₂: O_h
order 60, of type A₅: I
order 120, of type A₅ × Z₂: I_h

Impossible discrete symmetries

Since the overview is exhaustive, it also shows implicitly what is not possible as discrete symmetry group. For example:

a C₆ axis in one direction and a C₃ in another
a C₅ axis in one direction and a C₄ in another
a C₃ axis in one direction and another C₃ axis in a perpendicular direction

etc.

Fundamental domain

The fundamental domain

Fundamental domain

In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...

of a point group is a conic solid. An object with a given symmetry in a given orientation is characterized by the fundamental domain. If the object is a surface it is characterized by a surface in the fundamental domain continuing to its radial bordal faces or surface. If the copies of the surface do not fit, radial faces or surfaces can be added. They fit anyway if the fundamental domain is bounded by reflection planes.

For a polyhedron this surface in the fundamental domain can be part of an arbitrary plane. For example, in the disdyakis triacontahedron

Disdyakis triacontahedron

In geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons...

one full face is a fundamental domain. Adjusting the orientation of the plane gives various possibilities of combining two or more adjacent faces to one, giving various other polyhedra with the same symmetry. The polyhedron is convex if the surface fits to its copies and the radial line perpendicular to the plane is in the fundamental domain.

Also the surface in the fundamental domain may be composed of multiple faces.

Binary polyhedral groups

The map Spin(3) → SO(3) is the double cover of the rotation group by the spin group in 3 dimensions. (This is the only connected cover of SO(3), since Spin(3) is simply connected.)
By the lattice theorem

Lattice theorem

In mathematics, the lattice theorem, sometimes referred to as the fourth isomorphism theorem or the correspondence theorem, states that if N is a normal subgroup of a group G, then there exists a bijection from the set of all subgroups A of G such that A contains N, onto the set of all subgroups...

, there is a Galois connection

Galois connection

In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...

between subgroups of Spin(3) and subgroups of SO(3) (rotational point groups): the image of a subgroup of Spin(3) is a rotational point group, and the preimage of a point group is a subgroup of Spin(3).

The preimage of a finite point group is called a binary polyhedral group, represented as , and is called by the same name as its point group, with the prefix binary, with double the order of the related polyhedral group

Polyhedral group

In geometry, the polyhedral group is any of the symmetry groups of the Platonic solids. There are three polyhedral groups:*The tetrahedral group of order 12, rotational symmetry group of the regular tetrahedron....

(l,m,n). For instance, the preimage of the icosahedral group (2,3,5) is the binary icosahedral group, <2,3,5>.

The binary polyhedral groups are:

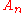: binary cyclic group of an (n + 1)-gon
: binary dihedral group of an n-gon, <2,2,n>
: binary tetrahedral group, <2,3,3>
: binary octahedral group, <2,3,4>
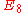: binary icosahedral group, <2,3,5>

These are classified by the ADE classification

ADE classification

In mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...

, and the quotient of C² by the action of a binary polyhedral group is a Du Val singularity

Du Val singularity

In algebraic geometry, a du Val singularity, also called simple surface singularity, Kleinian singularity, or rational double point, is a singularity of a surface that is a double cover branched over a curve with an A-D-E singularity. They are the canonical singularities in dimension 2...

.

For point groups that reverse orientation, the situation is more complicated, as there are two pin group

Pin group

In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....

s, so there are two possible binary groups corresponding to a given point group.

Note that this is a covering of groups, not a covering of spaces – the sphere is simply connected, and thus has no covering spaces. There is thus no notion of a "binary polyhedron" that covers a 3-dimensional polyhedron. Binary polyhedral groups are discrete subgroups of a Spin group, and under a representation of the spin group act on a vector space, and may stabilize a polyhedron in this representation – under the map Spin(3) → SO(3) they act on the same polyhedron that the underlying (non-binary) group acts on, while under spin representations or other representations they may stabilize other polyhedra.

This is in contrast to projective polyhedra – the sphere does cover projective space

Projective space

In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....

(and also lens space

Lens space

A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....

s), and thus a tessellation of projective space or lens space yields a distinct notion of polyhedron.

External links

Graphic overview of the 32 crystallographic point groups – form the first parts (apart from skipping n=5) of the 7 infinite series and 5 of the 7 separate 3D point groups
Overview of properties of point groups
Simplest Canonical Polyhedra of Each Symmetry Type (uses Java)
http://www.stanford.edu/~yishuwei/crystal.pdf Point Groups and Crystal Systems, by Yi-Shu Wei, pp. 4-6
The Geometry Center: 10.1 Formulas for Symmetries in Cartesian Coordinates (three dimensions)

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.