
Wallpaper group
Encyclopedia

Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
in the pattern. Such patterns occur frequently in architecture
Architecture
Architecture is both the process and product of planning, designing and construction. Architectural works, in the material form of buildings, are often perceived as cultural and political symbols and as works of art...
and decorative art
Decorative art
The decorative arts is traditionally a term for the design and manufacture of functional objects. It includes interior design, but not usually architecture. The decorative arts are often categorized in opposition to the "fine arts", namely, painting, drawing, photography, and large-scale...
. There are 17 possible distinct groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
Wallpaper groups are two-dimensional symmetry groups, intermediate in complexity between the simpler frieze group
Frieze group
A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s and the three-dimensional crystallographic groups (also called space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s).
Introduction
Wallpaper groups categorize patterns by their symmetries. Subtle differences may place similar patterns in different groups, while patterns that are very different in style, color, scale or orientation may belong to the same group.Consider the following examples:
Examples A and B have the same wallpaper group; it is called p4m in the IUC notation and *442 in the orbifold notation. Example C has a different wallpaper group, called p4g or 4*2 . The fact that A and B have the same wallpaper group means that they have the same symmetries, regardless of details of the designs, whereas C has a different set of symmetries despite any superficial similarities.
A complete list of all seventeen possible wallpaper groups can be found below.
Symmetries of patterns
A symmetrySymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of a pattern is, loosely speaking, a way of transforming the pattern so that the pattern looks exactly the same after the transformation. For example, translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
is present when the pattern can be translated (shifted) some finite distance and appear unchanged. Think of shifting a set of vertical stripes horizontally by one stripe. The pattern is unchanged. Strictly speaking, a true symmetry only exists in patterns that repeat exactly and continue indefinitely. A set of only, say, five stripes does not have translational symmetry — when shifted, the stripe on one end "disappears" and a new stripe is "added" at the other end. In practice, however, classification is applied to finite patterns, and small imperfections may be ignored.
Sometimes two categorizations are meaningful, one based on shapes alone and one also including colors. When colors are ignored there may be more symmetry. In black and white there are also 17 wallpaper groups; e.g., a colored tiling is equivalent with one in black and white with the colors coded radially in a circularly symmetric "bar code" in the centre of mass of each tile.
The types of transformations that are relevant here are called Euclidean plane isometries
Euclidean plane isometry
In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length...
. For example:
- If we shift example B one unit to the right, so that each square covers the square that was originally adjacent to it, then the resulting pattern is exactly the same as the pattern we started with. This type of symmetry is called a translationTranslationTranslation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
. Examples A and C are similar, except that the smallest possible shifts are in diagonal directions. - If we turn example B clockwise by 90°, around the centre of one of the squares, again we obtain exactly the same pattern. This is called a rotationRotationA rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
. Examples A and C also have 90° rotations, although it requires a little more ingenuity to find the correct centre of rotation for C. - We can also flip example B across a horizontal axis that runs across the middle of the image. This is called a reflectionReflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
. Example B also has reflections across a vertical axis, and across two diagonal axes. The same can be said for A.
However, example C is different. It only has reflections in horizontal and vertical directions, not across diagonal axes. If we flip across a diagonal line, we do not get the same pattern back; what we do get is the original pattern shifted across by a certain distance. This is part of the reason that the wallpaper group of A and B is different from the wallpaper group of C.
History
All 17 groups were used by Egyptian craftsmen, and used extensively in the Muslim world. A proofMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that there were only 17 possible patterns was first carried out by Evgraf Fedorov
Yevgraf Fyodorov
Yevgraf Stepanovich Fyodorov, sometimes spelled Evgraf Stepanovich Fedorov , was a Russian mathematician, crystallographer, and mineralogist....
in 1891 and then derived independently by George Pólya
George Pólya
George Pólya was a Hungarian mathematician. He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory...
in 1924.
Formal definition and discussion
Mathematically, a wallpaper group or plane crystallographic group is a type of topologically discreteDiscrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of isometries of the Euclidean plane
Euclidean plane isometry
In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length...
that contains two linearly independent translations.
Two such isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
s are of the same type (of the same wallpaper group) if they are the same up to an affine transformation of the plane. Thus e.g. a translation of the plane (hence a translation of the mirrors and centres of rotation) does not affect the wallpaper group. The same applies for a change of angle between translation vectors, provided that it does not add or remove any symmetry (this is only the case if there are no mirrors and no glide reflection
Glide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
s, and rotational symmetry is at most of order 2).
Unlike in the three-dimensional case, we can equivalently restrict the affine transformations to those that preserve orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
.
It follows from the Bieberbach theorem that all wallpaper groups are different even as abstract groups (as opposed to e.g. Frieze group
Frieze group
A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s, of which two are isomorphic with Z).
2D patterns with double translational symmetry can be categorized according to their symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
type.
Isometries of the Euclidean plane
Isometries of the Euclidean plane fall into four categories (see the article Euclidean plane isometryEuclidean plane isometry
In geometry, a Euclidean plane isometry is an isometry of the Euclidean plane, or more informally, a way of transforming the plane that preserves geometrical properties such as length...
for more information).
- Translations, denoted by Tv, where v is a vector in R2. This has the effect of shifting the plane applying displacementDisplacement (vector)A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
vector v. - Rotations, denoted by Rc,θ, where c is a point in the plane (the centre of rotation), and θ is the angle of rotation.
- ReflectionReflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s, or mirror isometries, denoted by FL, where L is a line in R2. (F is for "flip"). This has the effect of reflecting the plane in the line L, called the reflection axis or the associated mirror. - Glide reflectionGlide reflectionIn geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
s, denoted by GL,d, where L is a line in R2 and d is a distance. This is a combination of a reflection in the line L and a translation along L by a distance d.
The independent translations condition
The condition on linearly independent translations means that there exist linearly independent vectors v and w (in R2) such that the group contains both Tv and Tw.The purpose of this condition is to distinguish wallpaper groups from frieze group
Frieze group
A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s, which possess a translation but not two linearly independent ones, and from two-dimensional discrete point groups, which have no translations at all. In other words, wallpaper groups represent patterns that repeat themselves in two distinct directions, in contrast to frieze groups, which only repeat along a single axis.
(It is possible to generalise this situation. We could for example study discrete groups of isometries of Rn with m linearly independent translations, where m is any integer in the range 0 ≤ m ≤ n.)
The discreteness condition
The discreteness condition means that there is some positive real number ε, such that for every translation Tv in the group, the vector v has length at least ε (except of course in the case that v is the zero vector).The purpose of this condition is to ensure that the group has a compact fundamental domain, or in other words, a "cell" of nonzero, finite area, which is repeated through the plane. Without this condition, we might have for example a group containing the translation Tx for every rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
x, which would not correspond to any reasonable wallpaper pattern.
One important and nontrivial consequence of the discreteness condition in combination with the independent translations condition is that the group can only contain rotations of order 2, 3, 4, or 6; that is, every rotation in the group must be a rotation by 180°, 120°, 90°, or 60°. This fact is known as the crystallographic restriction theorem
Crystallographic restriction theorem
The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...
, and can be generalised to higher-dimensional cases.
Crystallographic notation
Crystallography has 230 space groupSpace group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s to distinguish, far more than the 17 wallpaper groups, but many of the symmetries in the groups are the same. Thus we can use a similar notation for both kinds of groups, that of Carl Hermann
Carl Hermann
Carl Hermann was a German professor of crystallography. With Charles-Victor Mauguin, he invented an international standard notation for crystallographic groups known as the Hermann–Mauguin notation or International notation.Born in the north German port town of Wesermünde to parents both of...
and Charles-Victor Mauguin
Charles-Victor Mauguin
French professor of mineralogy Charles-Victor Mauguin was inventor of an international standard notation for crystallographic groups known as the Hermann–Mauguin notation or International notation....
. An example of a full wallpaper name in Hermann-Mauguin style (also called IUC notation) is p31m, with four letters or digits; more usual is a shortened name like cmm or pg.
For wallpaper groups the full notation begins with either p or c, for a primitive cell
Primitive cell
Used predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions...
or a face-centred cell; these are explained below. This is followed by a digit, n, indicating the highest order of rotational symmetry: 1-fold (none), 2-fold, 3-fold, 4-fold, or 6-fold. The next two symbols indicate symmetries relative to one translation axis of the pattern, referred to as the "main" one; if there is a mirror perpendicular to a translation axis we choose that axis as the main one (or if there are two, one of them). The symbols are either m, g, or 1, for mirror, glide reflection, or none. The axis of the mirror or glide reflection is perpendicular to the main axis for the first letter, and either parallel or tilted 180°/n (when n > 2) for the second letter. Many groups include other symmetries implied by the given ones. The short notation drops digits or an m that can be deduced, so long as that leaves no confusion with another group.
A primitive cell is a minimal region repeated by lattice translations. All but two wallpaper symmetry groups are described with respect to primitive cell axes, a coordinate basis using the translation vectors of the lattice. In the remaining two cases symmetry description is with respect to centred cells that are larger than the primitive cell, and hence have internal repetition; the directions of their sides is different from those of the translation vectors spanning a primitive cell. Hermann-Mauguin notation for crystal space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s uses additional cell types.
Examples
- p2 (p211): Primitive cell, 2-fold rotation symmetry, no mirrors or glide reflections.
- p4g (p4gm): Primitive cell, 4-fold rotation, glide reflection perpendicular to main axis, mirror axis at 45°.
- cmm (c2mm): Centred cell, 2-fold rotation, mirror axes both perpendicular and parallel to main axis.
- p31m (p31m): Primitive cell, 3-fold rotation, mirror axis at 60°.
Here are all the names that differ in short and full notation.
| Short | p2 | pm | pg | cm | pmm | pmg | pgg | cmm | p4m | p4g | p6m |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Full | p211 | p1m1 | p1g1 | c1m1 | p2mm | p2mg | p2gg | c2mm | p4mm | p4gm | p6mm |
The remaining names are p1, p3, p3m1, p31m, p4, and p6.
Orbifold notation
Orbifold notation for wallpaper groups, introduced by John Horton ConwayJohn Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
(Conway, 1992) (Conway 2008), is based not on crystallography, but on topology. We fold the infinite periodic tiling of the plane into its essence, an orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
, then describe that with a few symbols.
- A digit, n, indicates a centre of n-fold rotation corresponding to a cone point on the orbifold. By the crystallographic restriction theorem, n must be 2, 3, 4, or 6.
- An asterisk, *, indicates a mirror symmetry corresponding to a boundary of the orbifold. It interacts with the digits as follows:
- Digits before * denote centres of pure rotation (cyclicPoint groupIn geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
). - Digits after * denote centres of rotation with mirrors through them, corresponding to "corners" on the boundary of the orbifold (dihedralDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
).
- Digits before * denote centres of pure rotation (cyclic
- A cross, x, occurs when a glide reflection is present and indicates a crosscap on the orbifold. Pure mirrors combine with lattice translation to produce glides, but those are already accounted for so we do not notate them.
- The "no symmetry" symbol, o, stands alone, and indicates we have only lattice translations with no other symmetry. The orbifold with this symbol is a torus; in general the symbol o denotes a handle on the orbifold.
Consider the group denoted in crystallographic notation by cmm; in Conway's notation, this will be 2*22. The 2 before the * says we have a 2-fold rotation centre with no mirror through it. The * itself says we have a mirror. The first 2 after the * says we have a 2-fold rotation centre on a mirror. The final 2 says we have an independent second 2-fold rotation centre on a mirror, one that is not a duplicate of the first one under symmetries.
The group denoted by pgg will be 22x. We have two pure 2-fold rotation centres, and a glide reflection axis. Contrast this with pmg, Conway 22*, where crystallographic notation mentions a glide, but one that is implicit in the other symmetries of the orbifold.
Coxeter's bracket notation is also included for comparison, based on reflectional Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s, and modified with plus superscripts for rotational symmetries.
| Conway | o | xx | *x | ** | 632 | *632 |
|---|---|---|---|---|---|---|
| Coxeter | [∞+,2,∞+] | [(∞,2)+,∞+] | [∞,2+,∞+] | [∞,2,∞+] | [6,3]+ | [6,3] |
| Crystal. | p1 | pg | cm | pm | p6 | p6m |
| Conway | 333 | *333 | 3*3 | 442 | *442 | 4*2 |
| Coxeter | [3[3]]+ | [3[3]] | [3+,6] | [4,4]+ | [4,4] | [4+,4] |
| Crystal. | p3 | p3m1 | p31m | p4 | p4m | p4g |
| Conway | 2222 | 22x | 22* | *2222 | 2*22 | |
| Coxeter | [∞,2,∞]+ | [∞+,2+,∞+] | [(∞,2)+,∞] | [∞,2,∞] | [∞,2+,∞] | |
| Crystal. | p2 | pgg | pmg | pmm | cmm |
Why there are exactly seventeen groups
An orbifold can be viewed as a polygonPolygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with face, edges, and vertices, which can be unfolded to form a possibly infinite set of polygons which tile either the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, the plane or the hyperbolic plane. When it tiles the plane it will give a wallpaper group and when it tiles the sphere or hyperbolic plane it gives either a spherical symmetry group or Hyperbolic symmetry group. The type of space the polygons tile can be found by calculating the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
, χ = V − E + F, where V is the number of corners (vertices), E is the number of edges and F is the number of faces. If the Euler characteristic is positive then the orbifold has a elliptic (spherical) structure; if it is zero then it has a parabolic structure, i.e. a wallpaper group; and if it is negative it will have a hyperbolic structure. When the full set of possible orbifolds is enumerated it is found that only 17 have Euler characteristic 0.
When an orbifold replicates by symmetry to fill the plane, its features create a structure of vertices, edges, and polygon faces, which must be consistent with the Euler characteristic. Reversing the process, we can assign numbers to the features of the orbifold, but fractions, rather than whole numbers. Because the orbifold itself is a quotient of the full surface by the symmetry group, the orbifold Euler characteristic is a quotient of the surface Euler characteristic by the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of the symmetry group.
The orbifold Euler characteristic is 2 minus the sum of the feature values, assigned as follows:
- A digit n before a * counts as (n−1)/n.
- A digit n after a * counts as (n−1)/2n.
- Both * and x count as 1.
- The "no symmetry" o counts as 2.
For a wallpaper group, the sum for the characteristic must be zero; thus the feature sum must be 2.
Examples
- 632: 5/6 + 2/3 + 1/2 = 2
- 3*3: 2/3 + 1 + 1/3 = 2
- 4*2: 3/4 + 1 + 1/4 = 2
- 22x: 1/2 + 1/2 + 1 = 2
Now enumeration of all wallpaper groups becomes a matter of arithmetic, of listing all feature strings with values summing to 2.
Incidentally, feature strings with other sums are not nonsense; they imply non-planar tilings, not discussed here. (When the orbifold Euler characteristic is negative, the tiling is hyperbolic; when positive, spherical or bad).
Guide to recognising wallpaper groups
To work out which wallpaper group corresponds to a given design, one may use the following table.| Size of smallest rotation | | Has reflection? | |||||
|---|---|---|---|---|---|---|
| Yes | No | |||||
| 360° / 6 | p6m | p6 | ||||
| 360° / 4 | Has mirrors at 45°? | p4 | ||||
| Yes: p4m | No: p4g | |||||
| 360° / 3 | Has rot. centre off mirrors? | p3 | ||||
| Yes: p31m | No: p3m1 | |||||
| 360° / 2 | Has perpendicular reflections? | Has glide reflection? | ||||
| Yes | No | |||||
| Has rot. centre off mirrors? | pmg | Yes: pgg | No: p2 | |||
| Yes: cmm | No: pmm | |||||
| none | Has glide axis off mirrors? | Has glide reflection? | ||||
| Yes: cm | No: pm | Yes: pg | No: p1 | |||
See also this overview with diagrams.
The seventeen groups
Each of the groups in this section has two cell structure diagrams, which are to be interpreted as follows:  |
a centre of rotation of order two (180°). |
 |
a centre of rotation of order three (120°). |
 |
a centre of rotation of order four (90°). |
 |
a centre of rotation of order six (60°). |
 |
an axis of reflection. |
 |
an axis of glide reflection. |
On the right-hand side diagrams, different equivalence classes of symmetry elements are colored (and rotated) differently.
The brown or yellow area indicates a fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
, i.e. the smallest part of the pattern that is repeated.
The diagrams on the right show the cell of the lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
corresponding to the smallest translations; those on the left sometimes show a larger area.
Group p1

- Orbifold notation: o.
- The group p1 contains only translations; there are no rotations, reflections, or glide reflections.
Examples of group p1
The two translations (cell sides) can each have different lengths, and can form any angle.
Group p2

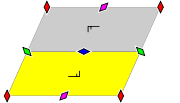
- Orbifold notation: 2222.
- The group p2 contains four rotation centres of order two (180°), but no reflections or glide reflections.
Examples of group p2
Group pm

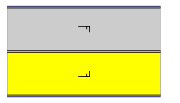
- Orbifold notation: **.
- The group pm has no rotations. It has reflection axes, they are all parallel.
Examples of group pm
(The first three have a vertical symmetry axis, and the last two each have a different diagonal one.)
Group pg


- Orbifold notation: xx.
- The group pg contains glide reflections only, and their axes are all parallel. There are no rotations or reflections.
Examples of group pg
Without the details inside the zigzag bands the mat is pmg; with the details but without the distinction between brown and black it is pgg.
Ignoring the wavy borders of the tiles, the pavement is pgg.
Group cm
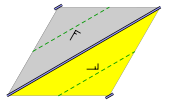
- Orbifold notation: *x.
- The group cm contains no rotations. It has reflection axes, all parallel. There is at least one glide reflection whose axis is not a reflection axis; it is halfway between two adjacent parallel reflection axes.
- This group applies for symmetrically staggered rows (i.e. there is a shift per row of half the translation distance inside the rows) of identical objects, which have a symmetry axis perpendicular to the rows.
Examples of group cm
Group pmm
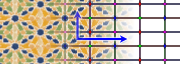
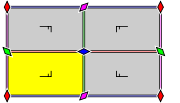
- Orbifold notation: *2222.
- The group pmm has reflections in two perpendicular directions, and four rotation centres of order two (180°) located at the intersections of the reflection axes.
Examples of group pmm
Group pmg
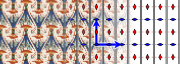
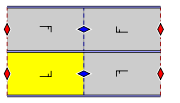
- Orbifold notation: 22*.
- The group pmg has two rotation centres of order two (180°), and reflections in only one direction. It has glide reflections whose axes are perpendicular to the reflection axes. The centres of rotation all lie on glide reflection axes.
Examples of group pmg
Group pgg
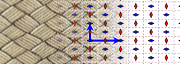
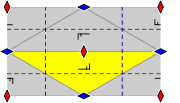
- Orbifold notation: 22x.
- The group pgg contains two rotation centres of order two (180°), and glide reflections in two perpendicular directions. The centres of rotation are not located on the glide reflection axes. There are no reflections.
Examples of group pgg
Group cmm
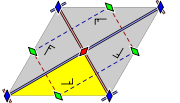
- Orbifold notation: 2*22.
- The group cmm has reflections in two perpendicular directions, and a rotation of order two (180°) whose centre is not on a reflection axis. It also has two rotations whose centres are on a reflection axis.
- This group is frequently seen in everyday life, since the most common arrangement of brickBrickA brick is a block of ceramic material used in masonry construction, usually laid using various kinds of mortar. It has been regarded as one of the longest lasting and strongest building materials used throughout history.-History:...
s in a brick building utilises this group (see example below).
The rotational symmetry of order 2 with centres of rotation at the centres of the sides of the rhombus is a consequence of the other properties.
The pattern corresponds to each of the following:
- symmetrically staggered rows of identical doubly symmetric objects
- a checkerboard pattern of two alternating rectangular tiles, of which each, by itself, is doubly symmetric
- a checkerboard pattern of alternatingly a 2-fold rotationally symmetric rectangular tile and its mirror image
Examples of group cmm
Group p4

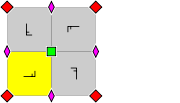
- Orbifold notation: 442.
- The group p4 has two rotation centres of order four (90°), and one rotation centre of order two (180°). It has no reflections or glide reflections.
Examples of group p4
A p4 pattern can be looked upon as a repetition in rows and columns of equal square tiles with 4-fold rotational symmetry. Also it can be looked upon as a checkerboard
Checkerboard
A checkerboard or chequerboard is a board of chequered pattern on which English draughts is played. It is an 8×8 board and the 64 squares are of alternating dark and light color, often red and black....
pattern of two such tiles, a factor
 smaller and rotated 45°.
smaller and rotated 45°.Group p4m
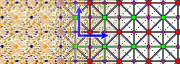
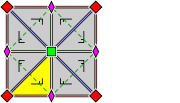
- Orbifold notation: *442.
- The group p4m has two rotation centres of order four (90°), and reflections in four distinct directions (horizontal, vertical, and diagonals). It has additional glide reflections whose axes are not reflection axes; rotations of order two (180°) are centred at the intersection of the glide reflection axes. All rotation centres lie on reflection axes.
This corresponds to a straightforward grid of rows and columns of equal squares with the four reflection axes. Also it corresponds to a checkerboard
Checkerboard
A checkerboard or chequerboard is a board of chequered pattern on which English draughts is played. It is an 8×8 board and the 64 squares are of alternating dark and light color, often red and black....
pattern of two of such squares.
Examples of group p4m
Examples displayed with the smallest translations horizontal and vertical (like in the diagram):
Examples displayed with the smallest translations diagonal (like on a checkerboard):
Group p4g
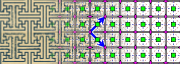
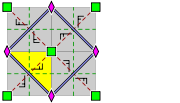
- Orbifold notation: 4*2.
- The group p4g has two centres of rotation of order four (90°), which are each other's mirror image, but it has reflections in only two directions, which are perpendicular. There are rotations of order two (180°) whose centres are located at the intersections of reflection axes. It has glide reflections axes parallel to the reflection axes, in between them, and also at an angle of 45° with these.
A p4g pattern can be looked upon as a checkerboard
Checkerboard
A checkerboard or chequerboard is a board of chequered pattern on which English draughts is played. It is an 8×8 board and the 64 squares are of alternating dark and light color, often red and black....
pattern of copies of a square tile with 4-fold rotational symmetry, and its mirror image. Alternatively it can be looked upon (by shifting half a tile) as a checkerboard pattern of copies of a horizontally and vertically symmetric tile and its 90° rotated version. Note that neither applies for a plain checkerboard pattern of black and white tiles, this is group p4m (with diagonal translation cells).
Note that the diagram on the left represents in area twice the smallest square that is repeated by translation.
Examples of group p4g
Group p3

- Orbifold notation: 333.
- The group p3 has three different rotation centres of order three (120°), but no reflections or glide reflections.
Imagine a tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the plane with equilateral triangles of equal size, with the sides corresponding to the smallest translations. Then half of the triangles are in one orientation, and the other half upside down. This wallpaper group corresponds to the case that all triangles of the same orientation are equal, while both types have rotational symmetry of order three, but the two are not equal, not each other's mirror image, and not both symmetric (if the two are equal we have p6, if they are each other's mirror image we have p31m, if they are both symmetric we have p3m1; if two of the three apply then the third also, and we have p6m). For a given image, three of these tessellations are possible, each with rotation centres as vertices, i.e. for any tessellation two shifts are possible. In terms of the image: the vertices can be the red, the blue or the green triangles.
Equivalently, imagine a tessellation of the plane with regular hexagons, with sides equal to the smallest translation distance divided by √3. Then this wallpaper group corresponds to the case that all hexagons are equal (and in the same orientation) and have rotational symmetry of order three, while they have no mirror image symmetry (if they have rotational symmetry of order six we have p6, if they are symmetric with respect to the main diagonals we have p31m, if they are symmetric with respect to lines perpendicular to the sides we have p3m1; if two of the three apply then the third also, and we have p6m). For a given image, three of these tessellations are possible, each with one third of the rotation centres as centres of the hexagons. In terms of the image: the centres of the hexagons can be the red, the blue or the green triangles.
Examples of group p3
Group p3m1
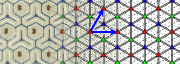
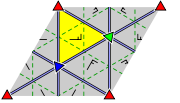
- Orbifold notation: *333.
- The group p3m1 has three different rotation centres of order three (120°). It has reflections in the three sides of an equilateral triangle. The centre of every rotation lies on a reflection axis. There are additional glide reflections in three distinct directions, whose axes are located halfway between adjacent parallel reflection axes.
Like for p3, imagine a tessellation of the plane with equilateral triangles of equal size, with the sides corresponding to the smallest translations. Then half of the triangles are in one orientation, and the other half upside down. This wallpaper group corresponds to the case that all triangles of the same orientation are equal, while both types have rotational symmetry of order three, and both are symmetric, but the two are not equal, and not each other's mirror image. For a given image, three of these tessellations are possible, each with rotation centres as vertices. In terms of the image: the vertices can be the red, the dark blue or the green triangles.
Examples of group p3m1
Group p31m
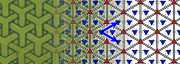
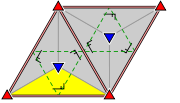
- Orbifold notation: 3*3.
- The group p31m has three different rotation centres of order three (120°), of which two are each other's mirror image. It has reflections in three distinct directions. It has at least one rotation whose centre does not lie on a reflection axis. There are additional glide reflections in three distinct directions, whose axes are located halfway between adjacent parallel reflection axes.
Like for p3 and p3m1, imagine a tessellation of the plane with equilateral triangles of equal size, with the sides corresponding to the smallest translations. Then half of the triangles are in one orientation, and the other half upside down. This wallpaper group corresponds to the case that all triangles of the same orientation are equal, while both types have rotational symmetry of order three and are each other's mirror image, but not symmetric themselves, and not equal. For a given image, only one such tessellation is possible. In terms of the image: the vertices can not be dark blue triangles.
Examples of group p31m
Group p6

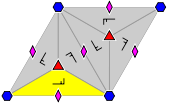
- Orbifold notation: 632.
- The group p6 has one rotation centre of order six, which only differ by a rotation of 60°; it has also two rotation centres of order three, which only differ by a rotation of 120° and three of order two (or, equivalently, 180°). It has no reflections or glide reflections.
A pattern with this symmetry can be looked upon as a tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the plane with equal triangular tiles with C3 symmetry, or equivalently, a tessellation of the plane with equal hexagonal tiles with C6 symmetry (with the edges of the tiles not necessarily part of the pattern).
Examples of group p6
Group p6m
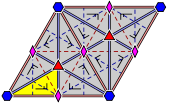
- Orbifold notation: *632.
- The group p6m has one rotation centre of order six (60°); it has also two rotation centres of order three, which only differ by a rotation of 60° (or, equivalently, 180°), and three of order two, which only differ by a rotation of 60°. It has also reflections in six distinct directions. There are additional glide reflections in six distinct directions, whose axes are located halfway between adjacent parallel reflection axes.
A pattern with this symmetry can be looked upon as a tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the plane with equal triangular tiles with D3 symmetry, or equivalently, a tessellation of the plane with equal hexagonal tiles with D6 symmetry (with the edges of the tiles not necessarily part of the pattern). Thus the simplest examples are a triangular lattice with or without connecting lines, and a hexagonal tiling with one color for outlining the hexagons and one for the background.
Examples of group p6m
Lattice types
There are five latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
types, corresponding to the five possible wallpaper groups of the lattice itself. The wallpaper group of a pattern with this lattice of translational symmetry cannot have more, but may have less symmetry than the lattice itself.
- In the 5 cases of rotational symmetry of order 3 or 6, the cell consists of two equilateral triangles (hexagonal lattice, itself p6m).
- In the 3 cases of rotational symmetry of order 4, the cell is a square (square lattice, itself p4m).
- In the 5 cases of reflection or glide reflection, but not both, the cell is a rectangle (rectangular lattice, itself pmm), therefore the diagrams show a rectangle, but a special case is that it actually is a square.
- In the 2 cases of reflection combined with glide reflection, the cell is a rhombus (rhombic lattice, itself cmm); a special case is that it actually is a square.
- In the case of only rotational symmetry of order 2, and the case of no other symmetry than translational, the cell is in general a parallelogram (parallelogrammatic lattice, itself p2), therefore the diagrams show a parallelogram, but special cases are that it actually is a rectangle, rhombus, or square.
Symmetry groups
The actual symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
should be distinguished from the wallpaper group. Wallpaper groups are collections of symmetry groups. There are 17 of these collections, but for each collection there are infinitely many symmetry groups, in the sense of actual groups of isometries. These depend, apart from the wallpaper group, on a number of parameters for the translation vectors, the orientation and position of the reflection axes and rotation centers.
The numbers of degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
are:
- 6 for p2
- 5 for pmm, pmg, pgg, and cmm
- 4 for the rest.
However, within each wallpaper group, all symmetry groups are algebraically isomorphic.
Some symmetry group isomorphisms:
- p1: Z2
- pm: Z × D∞
- pmm: D∞ × D∞.
Dependence of wallpaper groups on transformations
- The wallpaper group of a pattern is invariant under isometries and uniform scalingScaling (geometry)In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
(similarity transformationSimilarity (geometry)Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
s). - Translational symmetry is preserved under arbitrary bijective affine transformationAffine transformationIn geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s. - Rotational symmetry of order two ditto; this means also that 4- and 6-fold rotation centres at least keep 2-fold rotational symmetry.
- Reflection in a line and glide reflection are preserved on expansion/contraction along, or perpendicular to, the axis of reflection and glide reflection. It changes p6m, p4g, and p3m1 into cmm, p3m1 into cm, and p4m, depending on direction of expansion/contraction, into pmm or cmm. A pattern of symmetrically staggered rows of points is special in that it can convert by expansion/contraction from p6m to p4m.
Note that when a transformation decreases symmetry, a transformation of the same kind (the inverse) obviously for some patterns increases the symmetry. Such a special property of a pattern (e.g. expansion in one direction produces a pattern with 4-fold symmetry) is not counted as a form of extra symmetry.
Change of colors does not affect the wallpaper group if any two points that have the same color before the change, also have the same color after the change, and any two points that have different colors before the change, also have different colors after the change.
If the former applies, but not the latter, such as when converting a color image to one in black and white, then symmetries are preserved, but they may increase, so that the wallpaper group can change.
Web demo and software
There exist several software graphic tools that will let you create 2D patterns using wallpaper symmetry groups. Usually, you can edit the original tile and its copies in the entire pattern are updated automatically.- MadPattern, a free set of Adobe Illustrator templates that support the 17 wallpaper groups
- Tess, a nagware tessellation program for multiple platforms, supports all wallpaper, frieze, and rosette groups, as well as Heesch tilings.
- Kali, online graphical symmetry editor applet.
- Kali, free downloadable Kali for Windows and Mac Classic.
- InkscapeInkscapeInkscape is a free software vector graphics editor, licensed under the GNU General Public License. Its goal is to implement full support for the Scalable Vector Graphics 1.1 standard....
, a freeFree softwareFree software, software libre or libre software is software that can be used, studied, and modified without restriction, and which can be copied and redistributed in modified or unmodified form either without restriction, or with restrictions that only ensure that further recipients can also do...
vector graphics editorVector graphics editorA vector graphics editor is a computer program that allows users to compose and edit vector graphics images interactively on a computer and save them in one of many popular vector graphics formats, such as EPS, PDF, WMF, SVG, or VML....
, supports all 17 groups plus arbitrary scales, shifts, rotates, and color changes per row or per column, optionally randomized to a given degree. (See http://tavmjong.free.fr/INKSCAPE/MANUAL/html/Tiles-Symmetries.html) - SymmetryWorks is a commercial plugin for Adobe IllustratorAdobe IllustratorAdobe Illustrator is a vector graphics editor developed and marketed by Adobe Systems. Illustrator is similar in scope, intended market, and functionality to its competitors, CorelDraw, Xara Designer Pro and Macromedia FreeHand....
, supports all 17 groups. - Arabeske is a free standalone tool, supports a subset of wallpaper groups.
See also
- List of planar symmetry groups (summary of this page)
- TessellationTessellationA tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
- Point groupPoint groupIn geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
- CrystallographyCrystallographyCrystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
- Symmetry groups in one dimensionSymmetry groups in one dimensionA one-dimensional symmetry group is a mathematical group that describes symmetries in one dimension .A pattern in 1D can be represented as a function f for, say, the color at position x....
- Layer groupLayer groupIn mathematics, a layer group is a three-dimensional extension of a wallpaper group, with reflections in the third dimension. It is a space group with a two-dimensional lattice, meaning that it is symmetric over repeats in the two lattice directions...
- M. C. EscherM. C. EscherMaurits Cornelis Escher , usually referred to as M. C. Escher , was a Dutch graphic artist. He is known for his often mathematically inspired woodcuts, lithographs, and mezzotints...
- Aperiodic tilingAperiodic tilingAn aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
External links
- The 17 plane symmetry groups by David E. Joyce
- Introduction to wallpaper patterns by Chaim Goodman-Strauss and Heidi Burgiel
- Description by Silvio Levy
- Example tiling for each group, with dynamic demos of properties
- Overview with example tiling for each group
- Tiling plane and fancy by Steve Edwards
- Escher Web Sketch, a java applet with interactive tools for drawing in all 17 plane symmetry groups
- Burak, a Java applet for drawing symmetry groups.
- Beobachtungen zum geometrischen Motiv der Pelta
- Seventeen Kinds of Wallpaper Patterns the 17 symmetries found in traditional Japanese patterns.
- Math on the Walls- Natalie Wolchover

