Rotation group
Encyclopedia
In mechanics
and geometry
, the rotation group is the group
of all rotation
s about the origin of three-dimensional Euclidean space
R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation
that preserves length
of vectors (it is an isometry
) and preserves orientation
(i.e. handedness) of space. A length-preserving transformation which reverses orientation is an improper rotation
, that is a reflection or more generally a rotoinversion.
Composing two rotations results in another rotation; every rotation has a unique inverse rotation; and the identity map
satisfies the definition of a rotation. Owing to the above properties (along with the associative property, which rotations obey,) the set of all rotations is a group
under composition. Moreover, the rotation group has a natural manifold
structure for which the group operations are smooth
; so it is in fact a Lie group
. The rotation group is often denoted SO(3) for reasons explained below.
s between vectors. This follows from the fact that the standard dot product
between two vectors u and v can be written purely in terms of length: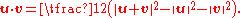
It follows that any length-preserving transformation in R3 preserves the dot product, and thus the angle between vectors. Rotations are often defined as linear transformations that preserve the inner product on R3. This is equivalent to requiring them to preserve length.
of R3 to another orthonormal basis. Like any linear transformation of finite-dimensional vector spaces, a rotation can always be represented by a matrix
. Let R be a given rotation. With respect to the standard basis
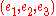of R3 the columns of R are given by 
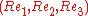. Since the standard basis is orthonormal, the columns of R form another orthonormal basis. This orthonormality condition can be expressed in the form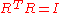
where RT denotes the transpose
of R and I is the 3 × 3 identity matrix
. Matrices for which this property holds are called orthogonal matrices
. The group of all 3 × 3 orthogonal matrices is denoted O(3), and consists of all proper and improper rotations.
In addition to preserving length, proper rotations must also preserve orientation. A matrix will preserve or reverse orientation according to whether the determinant
of the matrix is positive or negative. For an orthogonal matrix R, note that det RT = det R implies (det R)2 = 1 so that det R = ±1. The subgroup
of orthogonal matrices with determinant +1 is called the special orthogonal group, denoted SO(3).
Thus every rotation can be represented uniquely by an orthogonal matrix with unit determinant. Moreover, since composition of rotations corresponds to matrix multiplication
, the rotation group is isomorphic to the special orthogonal group SO(3).
Improper rotations correspond to orthogonal matrices with determinant −1, and they do not form a group because the product of two improper rotations is a proper rotation.
under function composition
(or equivalently the product of linear transformations). It is a subgroup
of the general linear group
consisting of all invertible linear transformations of Euclidean space.
Furthermore, the rotation group is nonabelian
. That is, the order in which rotations are composed makes a difference. For example, a quarter turn around the positive x-axis followed by a quarter turn around the positive y-axis is a different rotation than the one obtained by first rotating around y and then x.
The orthogonal group, consisting of all proper and improper rotations, is generated by reflections. Every proper rotation is the composition of two reflections, a special case of the Cartan–Dieudonné theorem.
which is called the axis of rotation (this is Euler's rotation theorem
). Each such rotation acts as an ordinary 2-dimensional rotation in the plane orthogonal to this axis. Since every 2-dimensional rotation can be represented by an angle φ, an arbitrary 3-dimensional rotation can be specified by an axis of rotation together with an angle of rotation
about this axis. (Technically, one needs to specify an orientation for the axis and whether the rotation is taken to be clockwise or counterclockwise with respect to this orientation).
For example, counterclockwise rotation about the positive z-axis by angle φ is given by
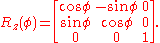
Given a unit vector n in R3 and an angle φ, let R(φ, n) represent a counterclockwise rotation about the axis through n (with orientation determined by n). Then
Using these properties one can show that any rotation can be represented by a unique angle φ in the range 0 ≤ φ ≤ π and a unit vector n such that
(or "glue together") antipodal point
s on the surface of the ball. After this identification, we arrive at a topological space
homeomorphic to the rotation group.
Indeed, the ball with antipodal surface points identified is a smooth manifold, and this manifold is diffeomorphic
to the rotation group. It is also diffeomorphic to the real 3-dimensional projective space
RP3, so the latter can also serve as a topological model for the rotation group.
These identifications illustrate that SO(3) is connected
but not simply connected. As to the latter, in the ball with antipodal surface points identified, consider the path running from the "north pole" straight through the interior down to the south pole. This is a closed loop, since the north pole and the south pole are identified. This loop cannot be shrunk to a point, since no matter how you deform the loop, the start and end point have to remain antipodal, or else the loop will "break open". In terms of rotations, this loop represents a continuous sequence of rotations about the z-axis starting and ending at the identity rotation (i.e. a series of rotation through an angle φ where φ runs from 0 to 2π
).
Surprisingly, if you run through the path twice, i.e., run from north pole down to south pole, jump back to the north pole (using the fact that north and south poles are identified), and then again run from north pole down to south pole, so that φ runs from 0 to 4π, you get a closed loop which can be shrunk to a single point: first move the paths continuously to the ball's surface, still connecting north pole to south pole twice. The second half of the path can then be mirrored over to the antipodal side without changing the path at all. Now we have an ordinary closed loop on the surface of the ball, connecting the north pole to itself along a great circle. This circle can be shrunk to the north pole without problems.
The same argument can be performed in general, and it shows that the fundamental group
of SO(3) is cyclic group
of order 2. In physics
applications, the non-triviality of the fundamental group allows for the existence of objects known as spinor
s, and is an important tool in the development of the spin-statistics theorem
.
The universal cover of SO(3) is a Lie group
called Spin(3). The group Spin(3) is isomorphic to the special unitary group
SU(2); it is also diffeomorphic to the unit 3-sphere
S3 and can be understood as the group of unit quaternions
(i.e. those with absolute value
1). The connection between quaternions and rotations, commonly exploited in computer graphics
, is explained in quaternions and spatial rotation
s. The map from S3 onto SO(3) that identifies antipodal points of S3 is a surjective homomorphism
of Lie groups, with kernel
{±1}. Topologically, this map is a two-to-one covering map
.
of the general linear group
GL(3), its Lie algebra
can be identified with a Lie subalgebra of gl(3), the algebra of 3×3 matrices with the commutator given by
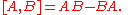
The condition that a matrix A belong to SO(3) is that
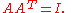
If A(t) is a one-parameter subgroup of SO(3) parametrised by t, then differentiating (*) with respect to t gives
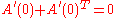
and so the Lie algebra so(3) consists of all skew-symmetric
3×3 matrices.
Another method is to specify an arbitrary rotation by a sequence of rotations about some fixed axes. See:
See charts on SO(3)
for further discussion.
, Rn. The group of all proper and improper rotations in n dimensions is called the orthogonal group
, O(n), and the subgroup of proper rotations is called the special orthogonal group, SO(n).
In special relativity
, one works in a 4-dimensional vector space, known as Minkowski space
rather than 3-dimensional Euclidean space. Unlike Euclidean space, Minkowski space has an inner product with an indefinite signature
. However, one can still define generalized rotations which preserve this inner product. Such generalized rotations are known as Lorentz transformation
s and the group of all such transformations is called the Lorentz group
.
The rotation group SO(3) can be described as a subgroup of E+(3), the Euclidean group
of direct isometries of R3. This larger group is the group of all motions of a rigid body
: each of these is a combination of a rotation about an arbitrary axis and a translation along the axis, or put differently, a combination of an element of SO(3) and an arbitrary translation.
In general, the rotation group of an object is the symmetry group
within the group of direct isometries; in other words, the intersection of the full symmetry group and the group of direct isometries. For chiral
objects it is the same as the full symmetry group.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the rotation group is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of all rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s about the origin of three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
that preserves length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
of vectors (it is an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
) and preserves orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
(i.e. handedness) of space. A length-preserving transformation which reverses orientation is an improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
, that is a reflection or more generally a rotoinversion.
Composing two rotations results in another rotation; every rotation has a unique inverse rotation; and the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
satisfies the definition of a rotation. Owing to the above properties (along with the associative property, which rotations obey,) the set of all rotations is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under composition. Moreover, the rotation group has a natural manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
structure for which the group operations are smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
; so it is in fact a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. The rotation group is often denoted SO(3) for reasons explained below.
Length and angle
Besides just preserving length, rotations also preserve the angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s between vectors. This follows from the fact that the standard dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
between two vectors u and v can be written purely in terms of length:
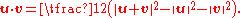
It follows that any length-preserving transformation in R3 preserves the dot product, and thus the angle between vectors. Rotations are often defined as linear transformations that preserve the inner product on R3. This is equivalent to requiring them to preserve length.
Orthogonal and rotation matrices
Every rotation maps an orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of R3 to another orthonormal basis. Like any linear transformation of finite-dimensional vector spaces, a rotation can always be represented by a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Let R be a given rotation. With respect to the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
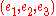of R3 the columns of R are given by 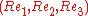. Since the standard basis is orthonormal, the columns of R form another orthonormal basis. This orthonormality condition can be expressed in the form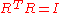where RT denotes the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of R and I is the 3 × 3 identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. Matrices for which this property holds are called orthogonal matrices
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
. The group of all 3 × 3 orthogonal matrices is denoted O(3), and consists of all proper and improper rotations.
In addition to preserving length, proper rotations must also preserve orientation. A matrix will preserve or reverse orientation according to whether the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the matrix is positive or negative. For an orthogonal matrix R, note that det RT = det R implies (det R)2 = 1 so that det R = ±1. The subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of orthogonal matrices with determinant +1 is called the special orthogonal group, denoted SO(3).
Thus every rotation can be represented uniquely by an orthogonal matrix with unit determinant. Moreover, since composition of rotations corresponds to matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, the rotation group is isomorphic to the special orthogonal group SO(3).
Improper rotations correspond to orthogonal matrices with determinant −1, and they do not form a group because the product of two improper rotations is a proper rotation.
Group structure
The rotation group is a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
(or equivalently the product of linear transformations). It is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
consisting of all invertible linear transformations of Euclidean space.
Furthermore, the rotation group is nonabelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
. That is, the order in which rotations are composed makes a difference. For example, a quarter turn around the positive x-axis followed by a quarter turn around the positive y-axis is a different rotation than the one obtained by first rotating around y and then x.
The orthogonal group, consisting of all proper and improper rotations, is generated by reflections. Every proper rotation is the composition of two reflections, a special case of the Cartan–Dieudonné theorem.
Axis of rotation
Every nontrivial proper rotation in 3 dimensions fixes a unique 1-dimensional linear subspace of R3Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
which is called the axis of rotation (this is Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
). Each such rotation acts as an ordinary 2-dimensional rotation in the plane orthogonal to this axis. Since every 2-dimensional rotation can be represented by an angle φ, an arbitrary 3-dimensional rotation can be specified by an axis of rotation together with an angle of rotation
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
about this axis. (Technically, one needs to specify an orientation for the axis and whether the rotation is taken to be clockwise or counterclockwise with respect to this orientation).
For example, counterclockwise rotation about the positive z-axis by angle φ is given by
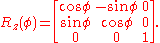
Given a unit vector n in R3 and an angle φ, let R(φ, n) represent a counterclockwise rotation about the axis through n (with orientation determined by n). Then
- R(0, n) is the identity transformation for any n
- R(φ, n) = R(−φ, −n)
- R(π + φ, n) = R(π − φ, −n).
Using these properties one can show that any rotation can be represented by a unique angle φ in the range 0 ≤ φ ≤ π and a unit vector n such that
- n is arbitrary if φ = 0
- n is unique if 0 < φ < π
- n is unique up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a sign if φ = π (that is, the rotations R(π, ±n) are identical).
Topology
Consider the solid ball in R3 of radius π (that is, all points of R3 of distance π or less from the origin). Given the above, for every point in this ball there is a rotation, with axis through the point and the origin, and rotation angle equal to the distance of the point from the origin. The identity rotation corresponds to the point at the center of the ball. Rotation through angles between 0 and −π correspond to the point on the same axis and distance from the origin but on the opposite side of the origin. The one remaining issue is that the two rotations through π and through -π are the same. So we identifyQuotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
(or "glue together") antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s on the surface of the ball. After this identification, we arrive at a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
homeomorphic to the rotation group.
Indeed, the ball with antipodal surface points identified is a smooth manifold, and this manifold is diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to the rotation group. It is also diffeomorphic to the real 3-dimensional projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
RP3, so the latter can also serve as a topological model for the rotation group.
These identifications illustrate that SO(3) is connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
but not simply connected. As to the latter, in the ball with antipodal surface points identified, consider the path running from the "north pole" straight through the interior down to the south pole. This is a closed loop, since the north pole and the south pole are identified. This loop cannot be shrunk to a point, since no matter how you deform the loop, the start and end point have to remain antipodal, or else the loop will "break open". In terms of rotations, this loop represents a continuous sequence of rotations about the z-axis starting and ending at the identity rotation (i.e. a series of rotation through an angle φ where φ runs from 0 to 2π
Turn (geometry)
A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
).
Surprisingly, if you run through the path twice, i.e., run from north pole down to south pole, jump back to the north pole (using the fact that north and south poles are identified), and then again run from north pole down to south pole, so that φ runs from 0 to 4π, you get a closed loop which can be shrunk to a single point: first move the paths continuously to the ball's surface, still connecting north pole to south pole twice. The second half of the path can then be mirrored over to the antipodal side without changing the path at all. Now we have an ordinary closed loop on the surface of the ball, connecting the north pole to itself along a great circle. This circle can be shrunk to the north pole without problems.
The same argument can be performed in general, and it shows that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of SO(3) is cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
applications, the non-triviality of the fundamental group allows for the existence of objects known as spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s, and is an important tool in the development of the spin-statistics theorem
Spin-statistics theorem
In quantum mechanics, the spin-statistics theorem relates the spin of a particle to the particle statistics it obeys. The spin of a particle is its intrinsic angular momentum...
.
The universal cover of SO(3) is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
called Spin(3). The group Spin(3) is isomorphic to the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
SU(2); it is also diffeomorphic to the unit 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
S3 and can be understood as the group of unit quaternions
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
(i.e. those with absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1). The connection between quaternions and rotations, commonly exploited in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, is explained in quaternions and spatial rotation
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
s. The map from S3 onto SO(3) that identifies antipodal points of S3 is a surjective homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of Lie groups, with kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
{±1}. Topologically, this map is a two-to-one covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
.
Lie algebra
Since SO(3) is a Lie subgroupLie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(3), its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
can be identified with a Lie subalgebra of gl(3), the algebra of 3×3 matrices with the commutator given by
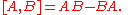
The condition that a matrix A belong to SO(3) is that
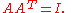
If A(t) is a one-parameter subgroup of SO(3) parametrised by t, then differentiating (*) with respect to t gives
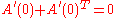
and so the Lie algebra so(3) consists of all skew-symmetric
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
3×3 matrices.
Representations of rotations
We have seen that there are a variety of ways to represent rotations:- as orthogonal matrices with determinant 1,
- by axis and rotation angle
- in quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
algebra with versors and the map S3 → SO(3) (see quaternions and spatial rotationQuaternions and spatial rotationUnit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
s).
Another method is to specify an arbitrary rotation by a sequence of rotations about some fixed axes. See:
- Euler angles
See charts on SO(3)
Charts on SO(3)
In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...
for further discussion.
Generalizations
The rotation group generalizes quite naturally to n-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, Rn. The group of all proper and improper rotations in n dimensions is called the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, O(n), and the subgroup of proper rotations is called the special orthogonal group, SO(n).
In special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, one works in a 4-dimensional vector space, known as Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
rather than 3-dimensional Euclidean space. Unlike Euclidean space, Minkowski space has an inner product with an indefinite signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
. However, one can still define generalized rotations which preserve this inner product. Such generalized rotations are known as Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s and the group of all such transformations is called the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
.
The rotation group SO(3) can be described as a subgroup of E+(3), the Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
of direct isometries of R3. This larger group is the group of all motions of a rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
: each of these is a combination of a rotation about an arbitrary axis and a translation along the axis, or put differently, a combination of an element of SO(3) and an arbitrary translation.
In general, the rotation group of an object is the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
within the group of direct isometries; in other words, the intersection of the full symmetry group and the group of direct isometries. For chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
objects it is the same as the full symmetry group.