
Pin group
Encyclopedia
In mathematics
, the pin group is a certain subgroup of the Clifford algebra
associated to a quadratic space. It maps 2-to-1 to the orthogonal group
, just as the spin group maps 2-to-1 to the special orthogonal group.
In general the map from the Pin group to the orthogonal group is not onto or a universal covering space, but if the quadratic form is definite (and dimension is greater than 2), it is both.
The non-trivial element of the kernel is denoted , which should not be confused with the orthogonal transform of reflection through the origin, generally denoted
, which should not be confused with the orthogonal transform of reflection through the origin, generally denoted  .
.
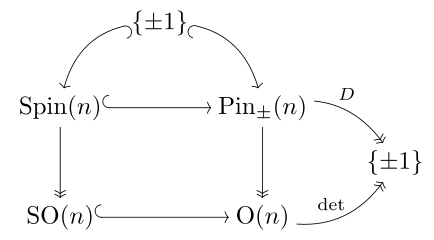
The pin group of a definite form maps onto the orthogonal group, and each component is simply connected: it double covers the orthogonal group. The pin groups for a positive definite quadratic form and for its negative
and for its negative  are not isomorphic, but the orthogonal groups are.In fact, they are equal as subsets of GL(V), not just isomorphic as abstract groups: an operator preserves a form if and only if it preserves the negative form.
are not isomorphic, but the orthogonal groups are.In fact, they are equal as subsets of GL(V), not just isomorphic as abstract groups: an operator preserves a form if and only if it preserves the negative form.
In terms of the standard forms, , but
, but  .
.
Using the "+" sign convention for Clifford algebras (where ), one writes
), one writes
and these both map onto .
.
By contrast, we have the natural isomorphismThey are subalgebras of the different algebras , but they are equal as subsets of the vector spaces
, but they are equal as subsets of the vector spaces  , and carry the same algebra structure, hence they are naturally identified.
, and carry the same algebra structure, hence they are naturally identified.  and they are both the (unique) double cover
and they are both the (unique) double cover
of the special orthogonal group SO(n), which is the (unique) universal cover for
, for , which correspond to the extensions of the center (which is either
, which correspond to the extensions of the center (which is either  or
or  ) by
) by  . Only two of them are pin groups—those that admit the Clifford algebra
. Only two of them are pin groups—those that admit the Clifford algebra
as a representation. They are called Pin(p,q) and Pin(q,p) respectively.
topological group
has a unique universal cover as a topological space, which has a unique group structure as a central extension by the fundamental group. For a disconnected topological group, there is a unique universal cover of the identity component of the group, and one can take the same cover as topological spaces on the other components (which are principal homogeneous space
s for the identity component) but the group structure on other components is not uniquely determined in general.
The Pin and Spin groups are particular topological groups associated to the orthogonal and special orthogonal groups, coming from Clifford algebras: there are other similar groups, corresponding to other double covers or to other group structures on the other components, but they are not referred to as Pin or Spin groups, nor studied much.
Recently, Andrzej Trautman
found the set of all 32 inequivalent double covers of O(p) x O(q), the maximal compact subgroup of O(p,q) and an explicit construction of 8 double covers of the same group O(p,q).

The group structure on (the connected component of determinant 1) is already determined; the group structure on the other component is determined up to the center, and thus has a
(the connected component of determinant 1) is already determined; the group structure on the other component is determined up to the center, and thus has a  ambiguity.
ambiguity.
The two extensions are distinguished by whether the preimage of a reflection squares to , and the two pin groups are named accordingly. Explicitly, a reflection has order 2 in
, and the two pin groups are named accordingly. Explicitly, a reflection has order 2 in  ,
,  , so the square of the preimage of a reflection (which has determinant one) must be in the kernel of
, so the square of the preimage of a reflection (which has determinant one) must be in the kernel of  , so
, so  , and either choice determines a pin group (since all reflections are conjugate by an element of
, and either choice determines a pin group (since all reflections are conjugate by an element of  , which is connected, all reflections must square to the same value).
, which is connected, all reflections must square to the same value).
Concretely, in ,
,  has order 2,
has order 2,
and the preimage of a subgroup is
is  :
:
if one repeats the same reflection
twice, one gets the identity.
In ,
,  has order 4,
has order 4,
and the preimage of a subgroup is
is  :
:
if one repeats the same reflection twice, one gets "a rotation
by 2π"—the non-trivial element of can be interpreted as "rotation by 2π" (every axis yields the same element).
can be interpreted as "rotation by 2π" (every axis yields the same element).
 and
and  mirrors the distinction between the dihedral group
mirrors the distinction between the dihedral group
of a -gon and the dicyclic group of the cyclic group
-gon and the dicyclic group of the cyclic group  .
.
In , the preimage of the dihedral group of an
, the preimage of the dihedral group of an  -gon, considered as a subgroup
-gon, considered as a subgroup  ,
,
is the dihedral group of an -gon,
-gon,  ,
,
while in , the preimage of the dihedral group is
, the preimage of the dihedral group is
the dicyclic group .
.
The resulting commutative square of subgroups for Spin(2), SO(2), O(2) – namely C2n, Dih2n, Cn, Dihn – is also obtained using the projective orthogonal group
SO(2), O(2) – namely C2n, Dih2n, Cn, Dihn – is also obtained using the projective orthogonal group
(going down from O by a 2-fold quotient, instead of up by a 2-fold cover) in the square SO(2), O(2), PSO(2), PO(2), though in this case it is also realized geometrically, as "the projectivization of a 2n-gon in the circle is an n-gon in the projective line".
In 1 dimension, the pin groups are congruent to the first dihedral and dicyclic groups:
".
It is a back-formation
from Spin: "Pin is to O(n) as Spin is to SO(n)", hence dropping the "S" from "Spin" yields "Pin". Further, the word "Pin" sounds like vulgar French slang when pronounced in French, which is alluded to by the name originating with (or being attributed to) Serre.French slang "pine" means "penis", and further, saying that the "pin group has 2 parts" (the even part (Spin) and the odd part) suggests proximate anatomical comparisons.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the pin group is a certain subgroup of the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
associated to a quadratic space. It maps 2-to-1 to the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, just as the spin group maps 2-to-1 to the special orthogonal group.
In general the map from the Pin group to the orthogonal group is not onto or a universal covering space, but if the quadratic form is definite (and dimension is greater than 2), it is both.
The non-trivial element of the kernel is denoted
 , which should not be confused with the orthogonal transform of reflection through the origin, generally denoted
, which should not be confused with the orthogonal transform of reflection through the origin, generally denoted  .
.Definite form

The pin group of a definite form maps onto the orthogonal group, and each component is simply connected: it double covers the orthogonal group. The pin groups for a positive definite quadratic form
 and for its negative
and for its negative  are not isomorphic, but the orthogonal groups are.In fact, they are equal as subsets of GL(V), not just isomorphic as abstract groups: an operator preserves a form if and only if it preserves the negative form.
are not isomorphic, but the orthogonal groups are.In fact, they are equal as subsets of GL(V), not just isomorphic as abstract groups: an operator preserves a form if and only if it preserves the negative form.In terms of the standard forms,
 , but
, but  .
.Using the "+" sign convention for Clifford algebras (where
 ), one writes
), one writes
and these both map onto
 .
.By contrast, we have the natural isomorphismThey are subalgebras of the different algebras
 , but they are equal as subsets of the vector spaces
, but they are equal as subsets of the vector spaces  , and carry the same algebra structure, hence they are naturally identified.
, and carry the same algebra structure, hence they are naturally identified.  and they are both the (unique) double cover
and they are both the (unique) double coverDouble cover
In mathematics, a double cover or double covering may refer to:*Double cover , a two-to-one mapping from one topological space to another...
of the special orthogonal group SO(n), which is the (unique) universal cover for

Indefinite form
There are as many as eight different double covers of Spin(p,q)Generalized orthogonal group
In mathematics, the indefinite orthogonal group, O is the Lie group of all linear transformations of a n = p + q dimensional real vector space which leave invariant a nondegenerate, symmetric bilinear form of signature...
, for
 , which correspond to the extensions of the center (which is either
, which correspond to the extensions of the center (which is either  or
or  ) by
) by  . Only two of them are pin groups—those that admit the Clifford algebra
. Only two of them are pin groups—those that admit the Clifford algebraClifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
as a representation. They are called Pin(p,q) and Pin(q,p) respectively.
As topological group
Every connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
has a unique universal cover as a topological space, which has a unique group structure as a central extension by the fundamental group. For a disconnected topological group, there is a unique universal cover of the identity component of the group, and one can take the same cover as topological spaces on the other components (which are principal homogeneous space
Principal homogeneous space
In mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G such that the stabilizer subgroup of any point is trivial...
s for the identity component) but the group structure on other components is not uniquely determined in general.
The Pin and Spin groups are particular topological groups associated to the orthogonal and special orthogonal groups, coming from Clifford algebras: there are other similar groups, corresponding to other double covers or to other group structures on the other components, but they are not referred to as Pin or Spin groups, nor studied much.
Recently, Andrzej Trautman
Andrzej Trautman
Andrzej Mariusz Trautman is a leading mathematical physicist who has made important contributions to classical gravitation in general and to general relativity in particular....
found the set of all 32 inequivalent double covers of O(p) x O(q), the maximal compact subgroup of O(p,q) and an explicit construction of 8 double covers of the same group O(p,q).
Construction
The two pin groups correspond to the two central extensions
The group structure on
 (the connected component of determinant 1) is already determined; the group structure on the other component is determined up to the center, and thus has a
(the connected component of determinant 1) is already determined; the group structure on the other component is determined up to the center, and thus has a  ambiguity.
ambiguity.The two extensions are distinguished by whether the preimage of a reflection squares to
 , and the two pin groups are named accordingly. Explicitly, a reflection has order 2 in
, and the two pin groups are named accordingly. Explicitly, a reflection has order 2 in  ,
,  , so the square of the preimage of a reflection (which has determinant one) must be in the kernel of
, so the square of the preimage of a reflection (which has determinant one) must be in the kernel of  , so
, so  , and either choice determines a pin group (since all reflections are conjugate by an element of
, and either choice determines a pin group (since all reflections are conjugate by an element of  , which is connected, all reflections must square to the same value).
, which is connected, all reflections must square to the same value).Concretely, in
 ,
,  has order 2,
has order 2,and the preimage of a subgroup
 is
is  :
:if one repeats the same reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
twice, one gets the identity.
In
 ,
,  has order 4,
has order 4,and the preimage of a subgroup
 is
is  :
:if one repeats the same reflection twice, one gets "a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
by 2π"—the non-trivial element of
 can be interpreted as "rotation by 2π" (every axis yields the same element).
can be interpreted as "rotation by 2π" (every axis yields the same element).Low dimensions
In 2 dimensions, the distinction between and
and  mirrors the distinction between the dihedral group
mirrors the distinction between the dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of a
 -gon and the dicyclic group of the cyclic group
-gon and the dicyclic group of the cyclic group  .
.In
 , the preimage of the dihedral group of an
, the preimage of the dihedral group of an  -gon, considered as a subgroup
-gon, considered as a subgroup  ,
,is the dihedral group of an
 -gon,
-gon,  ,
,while in
 , the preimage of the dihedral group is
, the preimage of the dihedral group isthe dicyclic group
 .
.The resulting commutative square of subgroups for Spin(2),
 SO(2), O(2) – namely C2n, Dih2n, Cn, Dihn – is also obtained using the projective orthogonal group
SO(2), O(2) – namely C2n, Dih2n, Cn, Dihn – is also obtained using the projective orthogonal groupProjective orthogonal group
In projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space V = A quadratic space is a vector space V together with a quadratic form Q; the Q is dropped from notation when it is clear. on the associated projective...
(going down from O by a 2-fold quotient, instead of up by a 2-fold cover) in the square SO(2), O(2), PSO(2), PO(2), though in this case it is also realized geometrically, as "the projectivization of a 2n-gon in the circle is an n-gon in the projective line".
In 1 dimension, the pin groups are congruent to the first dihedral and dicyclic groups:

Name
The name was introduced in , where they state "This joke is due to J-P. SerreJean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
".
It is a back-formation
Back-formation
In etymology, back-formation is the process of creating a new lexeme, usually by removing actual or supposed affixes. The resulting neologism is called a back-formation, a term coined by James Murray in 1889...
from Spin: "Pin is to O(n) as Spin is to SO(n)", hence dropping the "S" from "Spin" yields "Pin". Further, the word "Pin" sounds like vulgar French slang when pronounced in French, which is alluded to by the name originating with (or being attributed to) Serre.French slang "pine" means "penis", and further, saying that the "pin group has 2 parts" (the even part (Spin) and the odd part) suggests proximate anatomical comparisons.

