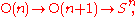Orthogonal group
Encyclopedia
In mathematics
, the orthogonal group of degree n over a field
F (written as O(n,F)) is the group
of n × n orthogonal matrices
with entries from F, with the group operation of matrix multiplication
. This is a subgroup
of the general linear group
GL(n,F) given by

where QT is the transpose
of Q. The classical orthogonal group over the real numbers is usually just written O(n).
More generally the orthogonal group of a non-singular quadratic form
over F is the group of linear operators preserving the form – the above group O(n, F) is then the orthogonal group of the sum-of-n-squares quadratic form. The Cartan–Dieudonné theorem describes the structure of the orthogonal group for non-singular form. This article only discusses definite forms
– the orthogonal group of the positive definite form (equivalent to sum of n squares) and negative definite forms (equivalent to the negative sum of n squares) are identical – – though the associated Pin group
– though the associated Pin group
s differ; for other non-singular forms O(p,q), see indefinite orthogonal group.
Every orthogonal matrix has determinant
either 1 or −1. The orthogonal n-by-n matrices with determinant 1 form a normal subgroup
of O(n,F) known as the special orthogonal group, SO(n,F). (More precisely, SO(n,F) is the kernel of the Dickson invariant, discussed below.) By analogy with GL/SL (general linear group, special linear group), the orthogonal group is sometimes called the general orthogonal group and denoted GO, though this term is also sometimes used for indefinite orthogonal groups O(p,q).
The derived subgroup
Ω(n,F) of O(n,F) is an often studied object because when F is a finite field Ω(n,F) is often a central extension of a finite simple group.
Both O(n,F) and SO(n,F) are algebraic group
s, because the condition that a matrix be orthogonal, i.e. have its own transpose
as inverse, can be expressed as a set of polynomial equations in the entries of the matrix.
s, the orthogonal group O(n,R) and the special orthogonal group SO(n,R) are often simply denoted by O(n) and SO(n) if no confusion is possible. They form real compact
Lie group
s of dimension
n(n − 1)/2. O(n,R) has two connected components
, with SO(n,R) being the identity component
, i.e., the connected component containing the identity matrix
.
The real orthogonal and real special orthogonal groups have the following geometric interpretations:
O(n,R) is a subgroup of the Euclidean group
E(n), the group of isometries
of Rn; it contains those that leave the origin fixed – O(n,R) = E(n) ∩ GL(n,R). It is the symmetry group of the sphere
(n = 3) or hypersphere
and all objects with spherical symmetry, if the origin is chosen at the center.
SO(n,R) is a subgroup of E+(n), which consists of direct isometries, i.e., isometries preserving orientation
; it contains those that leave the origin fixed – It is the rotation group of the sphere and all objects with spherical symmetry, if the origin is chosen at the center.
It is the rotation group of the sphere and all objects with spherical symmetry, if the origin is chosen at the center.
{ I, −I } is a normal subgroup
and even a characteristic subgroup
of O(n,R), and, if n is even, also of SO(n,R). If n is odd, O(n,R) is the direct product
of SO(n,R) and { I, −I }. The cyclic group
of k-fold rotation
s Ck is for every positive integer k a normal subgroup of O(2,R) and SO(2,R).
Relative to suitable orthogonal bases, the isometries are of the form:
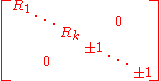
where the matrices R1,...,Rk are 2-by-2 rotation matrices in orthogonal planes of rotation. As a special case, known as Euler's rotation theorem
, any (non-identity) element of SO(3,R) is rotation about a uniquely defined axis.
The orthogonal group is generated by reflections (two reflections give a rotation
), as in a Coxeter group
,The analogy is stronger: Weyl groups, a class of (representations of) Coxeter groups, can be considered as simple algebraic groups over the field with one element
, and there are a number of analogies between algebraic groups and vector spaces on the one hand, and Weyl groups and sets on the other. and elements have length
at most n (require at most n reflections to generate; this follows from the above classification, noting that a rotation is generated by 2 reflections, and is true more generally for indefinite orthogonal groups, by the Cartan–Dieudonné theorem). A longest element
(element needing the most reflections) is reflection through the origin (the map ), though so are other maximal combinations of rotations (and a reflection, in odd dimension).
), though so are other maximal combinations of rotations (and a reflection, in odd dimension).
The symmetry group
of a circle
is O(2,R), also called Dih
(S1), where S1 denotes the multiplicative group of complex number
s of absolute value
1.
SO(2,R) is isomorphic (as a Lie group) to the circle S1 (circle group). This isomorphism sends the complex number exp(φi) = cos(φ) + i sin(φ) to the orthogonal matrix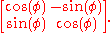
The group SO(3,R), understood as the set of rotations of 3-dimensional space, is of major importance in the sciences and engineering. See rotation group
and the general formula for a 3 × 3 rotation matrix in terms of the axis and the angle.
In terms of algebraic topology
, for n > 2 the fundamental group
of SO(n,R) is cyclic of order 2
, and the spinor group Spin(n) is its universal cover. For n = 2 the fundamental group is infinite cyclic and the universal cover corresponds to the real line
(the spinor group Spin(2) is the unique 2-fold cover).
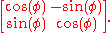 (reflection through the origin) is orientation-preserving in even dimension, but orientation-reversing in odd dimension. When this distinction wishes to be emphasized, the groups are generally denoted O(2k) and O(2k+1), reserving n for the dimension of the space (
(reflection through the origin) is orientation-preserving in even dimension, but orientation-reversing in odd dimension. When this distinction wishes to be emphasized, the groups are generally denoted O(2k) and O(2k+1), reserving n for the dimension of the space ( or
or 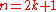 ). The letters p or r are also used,
). The letters p or r are also used,
indicating the rank of the corresponding Lie algebra
; in odd dimension the corresponding Lie algebra is while in even dimension the Lie algebra is
while in even dimension the Lie algebra is 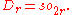
associated to the Lie groups O(n,R) and SO(n,R) consists of the skew-symmetric
real n-by-n matrices, with the Lie bracket
given by the commutator
. This Lie algebra is often denoted by o(n,R) or by so(n,R), and called the or . These Lie algebras are the compact real forms of two of the four families of semisimple Lie algebras: in odd dimension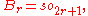 while in even dimension
while in even dimension 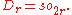
More intrinsically, given a vector space with an inner product, the special orthogonal Lie algebra is given by the bivector
s on the space, which are sums of simple bivectors (2-blades) . The correspondence is given by the map
. The correspondence is given by the map 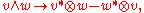 where
where  is the covector dual to the vector v; in coordinates these are exactly the elementary skew-symmetric matrices.
is the covector dual to the vector v; in coordinates these are exactly the elementary skew-symmetric matrices.
This characterization is used in interpreting the curl of a vector field (naturally a 2-vector) as an infinitesimal rotation or "curl", hence the name. Generalizing the inner product with a nondegenerate form yields the indefinite orthogonal Lie algebras
The representation theory of the orthogonal Lie algebras includes both representations corresponding to linear representations of the orthogonal groups, and representations corresponding to projective representations of the orthogonal groups (linear representations of spin groups), the so-called spin representation, which are important in physics.
the same with inversion in the origin ( x is mapped to −x), i.e. respectively:
The 4th and 5th in particular, and in a wider sense the 6th also, are called improper rotation
s.
See also the similar overview including translations.
s, though not all conformal linear transforms are orthogonal. In classical terms this is the difference between congruence
and similarity
, as exemplified by SSS (Side-Side-Side) congruence of triangles and AAA (Angle-Angle-Angle) similarity of triangles. The group of conformal linear maps of Rn is denoted CO(n) for the conformal orthogonal group, and consists of the product of the orthogonal group with the group of dilation
s. If n is odd, these two subgroups do not intersect, and they are a direct product
: , while if n is even, these subgroups intersect in
, while if n is even, these subgroups intersect in  , so this is not a direct product, but it is a direct product with the subgroup of dilation by a positive scalar:
, so this is not a direct product, but it is a direct product with the subgroup of dilation by a positive scalar:  .
.
Similarly one can define CSO(n); note that this is always : .
.
s, O(n,C) and SO(n,C) are complex Lie groups of dimension n(n − 1)/2 over C (which means the dimension over R is twice that). O(n,C) has two connected components, and SO(n,C) is the connected component containing the identity matrix. For n ≥ 2 these groups are noncompact.
Just as in the real case SO(n,C) is not simply connected. For n > 2 the fundamental group
of SO(n,C) is cyclic of order 2
whereas the fundamental group of SO(2,C) is infinite cyclic.
The complex Lie algebra
associated to O(n,C) and SO(n,C) consists of the skew-symmetric complex n-by-n matrices, with the Lie bracket given by the commutator
.
s: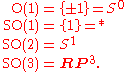
The group is double covered by
is double covered by 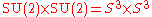 .
.
There are numerous charts on SO(3)
, due to the importance of 3-dimensional rotations in engineering applications.
Here Sn denotes the n-dimensional sphere, RPn the n-dimensional real projective space
, and SU(n) the special unitary group
of degree n.
, and thus are in general hard to compute.
However, one can compute the homotopy groups of the stable orthogonal group (aka the infinite orthogonal group), defined as the direct limit
of the sequence of inclusions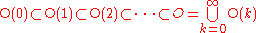
(as the inclusions are all closed inclusions, hence cofibration
s, this can also be interpreted as a union).
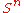 is a homogeneous space
is a homogeneous space
for , and one has the following fiber bundle
, and one has the following fiber bundle
:
which can be understood as "The orthogonal group acts transitively on the unit sphere
acts transitively on the unit sphere 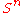 , and the stabilizer of a point (thought of as a unit vector) is the orthogonal group of the perpendicular complement, which is an orthogonal group one dimension lower". The map
, and the stabilizer of a point (thought of as a unit vector) is the orthogonal group of the perpendicular complement, which is an orthogonal group one dimension lower". The map  is the natural inclusion.
is the natural inclusion.
Thus the inclusion is (n − 1)-connected
is (n − 1)-connected
, so the homotopy groups stabilize, and for
for 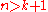 : thus the homotopy groups of the stable space equal the lower homotopy groups of the unstable spaces.
: thus the homotopy groups of the stable space equal the lower homotopy groups of the unstable spaces.
Via Bott periodicity, , thus the homotopy groups of O are 8-fold periodic, meaning
, thus the homotopy groups of O are 8-fold periodic, meaning  , and one needs only to compute the lower 8 homotopy groups to compute them all.
, and one needs only to compute the lower 8 homotopy groups to compute them all.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the orthogonal group of degree n over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F (written as O(n,F)) is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of n × n orthogonal matrices
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
with entries from F, with the group operation of matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. This is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n,F) given by

where QT is the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of Q. The classical orthogonal group over the real numbers is usually just written O(n).
More generally the orthogonal group of a non-singular quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
over F is the group of linear operators preserving the form – the above group O(n, F) is then the orthogonal group of the sum-of-n-squares quadratic form. The Cartan–Dieudonné theorem describes the structure of the orthogonal group for non-singular form. This article only discusses definite forms
Definite quadratic form
In mathematics, a definite quadratic form is a real-valued quadratic form over some vector space V that has the same sign for every nonzero vector of V...
– the orthogonal group of the positive definite form (equivalent to sum of n squares) and negative definite forms (equivalent to the negative sum of n squares) are identical –
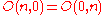 – though the associated Pin group
– though the associated Pin groupPin group
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
s differ; for other non-singular forms O(p,q), see indefinite orthogonal group.
Every orthogonal matrix has determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
either 1 or −1. The orthogonal n-by-n matrices with determinant 1 form a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of O(n,F) known as the special orthogonal group, SO(n,F). (More precisely, SO(n,F) is the kernel of the Dickson invariant, discussed below.) By analogy with GL/SL (general linear group, special linear group), the orthogonal group is sometimes called the general orthogonal group and denoted GO, though this term is also sometimes used for indefinite orthogonal groups O(p,q).
The derived subgroup
Commutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
Ω(n,F) of O(n,F) is an often studied object because when F is a finite field Ω(n,F) is often a central extension of a finite simple group.
Both O(n,F) and SO(n,F) are algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s, because the condition that a matrix be orthogonal, i.e. have its own transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
as inverse, can be expressed as a set of polynomial equations in the entries of the matrix.
Over the real number field
Over the field R of real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, the orthogonal group O(n,R) and the special orthogonal group SO(n,R) are often simply denoted by O(n) and SO(n) if no confusion is possible. They form real compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s of dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
n(n − 1)/2. O(n,R) has two connected components
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, with SO(n,R) being the identity component
Identity component
In mathematics, the identity component of a topological group G is the connected component G0 of G that contains the identity element of the group...
, i.e., the connected component containing the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
The real orthogonal and real special orthogonal groups have the following geometric interpretations:
O(n,R) is a subgroup of the Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
E(n), the group of isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of Rn; it contains those that leave the origin fixed – O(n,R) = E(n) ∩ GL(n,R). It is the symmetry group of the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
(n = 3) or hypersphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
and all objects with spherical symmetry, if the origin is chosen at the center.
SO(n,R) is a subgroup of E+(n), which consists of direct isometries, i.e., isometries preserving orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
; it contains those that leave the origin fixed –
 It is the rotation group of the sphere and all objects with spherical symmetry, if the origin is chosen at the center.
It is the rotation group of the sphere and all objects with spherical symmetry, if the origin is chosen at the center.{ I, −I } is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
and even a characteristic subgroup
Characteristic subgroup
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
of O(n,R), and, if n is even, also of SO(n,R). If n is odd, O(n,R) is the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of SO(n,R) and { I, −I }. The cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of k-fold rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s Ck is for every positive integer k a normal subgroup of O(2,R) and SO(2,R).
Relative to suitable orthogonal bases, the isometries are of the form:
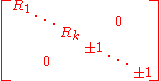
where the matrices R1,...,Rk are 2-by-2 rotation matrices in orthogonal planes of rotation. As a special case, known as Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
, any (non-identity) element of SO(3,R) is rotation about a uniquely defined axis.
The orthogonal group is generated by reflections (two reflections give a rotation
Coordinate rotations and reflections
In geometry, 2D coordinate rotations and reflections are two kinds of Euclidean plane isometries which are related to one another.A rotation in the plane can be formed by composing a pair of reflections. First reflect a point P to its image P′ on the other side of line L1...
), as in a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
,The analogy is stronger: Weyl groups, a class of (representations of) Coxeter groups, can be considered as simple algebraic groups over the field with one element
Field with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
, and there are a number of analogies between algebraic groups and vector spaces on the one hand, and Weyl groups and sets on the other. and elements have length
Length function
In mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
at most n (require at most n reflections to generate; this follows from the above classification, noting that a rotation is generated by 2 reflections, and is true more generally for indefinite orthogonal groups, by the Cartan–Dieudonné theorem). A longest element
Longest element of a Coxeter group
In mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
(element needing the most reflections) is reflection through the origin (the map
 ), though so are other maximal combinations of rotations (and a reflection, in odd dimension).
), though so are other maximal combinations of rotations (and a reflection, in odd dimension).The symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is O(2,R), also called Dih
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
(S1), where S1 denotes the multiplicative group of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
1.
SO(2,R) is isomorphic (as a Lie group) to the circle S1 (circle group). This isomorphism sends the complex number exp(φi) = cos(φ) + i sin(φ) to the orthogonal matrix
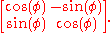
The group SO(3,R), understood as the set of rotations of 3-dimensional space, is of major importance in the sciences and engineering. See rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
and the general formula for a 3 × 3 rotation matrix in terms of the axis and the angle.
In terms of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, for n > 2 the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of SO(n,R) is cyclic of order 2
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
, and the spinor group Spin(n) is its universal cover. For n = 2 the fundamental group is infinite cyclic and the universal cover corresponds to the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
(the spinor group Spin(2) is the unique 2-fold cover).
Even and odd dimension
The structure of the orthogonal group differs in certain respects between even and odd dimensions – for example,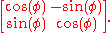 (reflection through the origin) is orientation-preserving in even dimension, but orientation-reversing in odd dimension. When this distinction wishes to be emphasized, the groups are generally denoted O(2k) and O(2k+1), reserving n for the dimension of the space (
(reflection through the origin) is orientation-preserving in even dimension, but orientation-reversing in odd dimension. When this distinction wishes to be emphasized, the groups are generally denoted O(2k) and O(2k+1), reserving n for the dimension of the space ( or
or 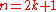 ). The letters p or r are also used,
). The letters p or r are also used,indicating the rank of the corresponding Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
; in odd dimension the corresponding Lie algebra is
 while in even dimension the Lie algebra is
while in even dimension the Lie algebra is 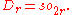
Lie algebra
The Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
associated to the Lie groups O(n,R) and SO(n,R) consists of the skew-symmetric
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
real n-by-n matrices, with the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
given by the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
. This Lie algebra is often denoted by o(n,R) or by so(n,R), and called the or . These Lie algebras are the compact real forms of two of the four families of semisimple Lie algebras: in odd dimension
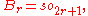 while in even dimension
while in even dimension 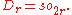
More intrinsically, given a vector space with an inner product, the special orthogonal Lie algebra is given by the bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s on the space, which are sums of simple bivectors (2-blades)
 . The correspondence is given by the map
. The correspondence is given by the map 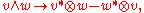 where
where  is the covector dual to the vector v; in coordinates these are exactly the elementary skew-symmetric matrices.
is the covector dual to the vector v; in coordinates these are exactly the elementary skew-symmetric matrices.This characterization is used in interpreting the curl of a vector field (naturally a 2-vector) as an infinitesimal rotation or "curl", hence the name. Generalizing the inner product with a nondegenerate form yields the indefinite orthogonal Lie algebras
The representation theory of the orthogonal Lie algebras includes both representations corresponding to linear representations of the orthogonal groups, and representations corresponding to projective representations of the orthogonal groups (linear representations of spin groups), the so-called spin representation, which are important in physics.
3D isometries that leave the origin fixed
Isometries of R3 that leave the origin fixed, forming the group O(3,R), can be categorized as:- SO(3,
- identity
- rotation about an axis through the origin by an angle not equal to 180°
- rotation about an axis through the origin by an angle of 180°
- inversion in the origin
- rotation about an axis by an angle not equal to 180°, combined with reflection in the plane through the origin perpendicular to the axis
- reflection in a plane through the origin.
The 4th and 5th in particular, and in a wider sense the 6th also, are called improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
s.
See also the similar overview including translations.
Conformal group
Being isometries (preserving distances), orthogonal transforms also preserve angles, and are thus conformal mapConformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
s, though not all conformal linear transforms are orthogonal. In classical terms this is the difference between congruence
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
and similarity
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
, as exemplified by SSS (Side-Side-Side) congruence of triangles and AAA (Angle-Angle-Angle) similarity of triangles. The group of conformal linear maps of Rn is denoted CO(n) for the conformal orthogonal group, and consists of the product of the orthogonal group with the group of dilation
Dilation (mathematics)
In mathematics, a dilation is a function f from a metric space into itself that satisfies the identityd=rd \,for all points where d is the distance from x to y and r is some positive real number....
s. If n is odd, these two subgroups do not intersect, and they are a direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
:
 , while if n is even, these subgroups intersect in
, while if n is even, these subgroups intersect in  , so this is not a direct product, but it is a direct product with the subgroup of dilation by a positive scalar:
, so this is not a direct product, but it is a direct product with the subgroup of dilation by a positive scalar:  .
.Similarly one can define CSO(n); note that this is always :
 .
.Over the complex number field
Over the field C of complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, O(n,C) and SO(n,C) are complex Lie groups of dimension n(n − 1)/2 over C (which means the dimension over R is twice that). O(n,C) has two connected components, and SO(n,C) is the connected component containing the identity matrix. For n ≥ 2 these groups are noncompact.
Just as in the real case SO(n,C) is not simply connected. For n > 2 the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of SO(n,C) is cyclic of order 2
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
whereas the fundamental group of SO(2,C) is infinite cyclic.
The complex Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
associated to O(n,C) and SO(n,C) consists of the skew-symmetric complex n-by-n matrices, with the Lie bracket given by the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
.
Low dimensional
The low dimensional (real) orthogonal groups are familiar spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s:
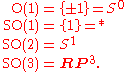
The group
 is double covered by
is double covered by 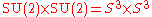 .
.There are numerous charts on SO(3)
Charts on SO(3)
In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...
, due to the importance of 3-dimensional rotations in engineering applications.
Here Sn denotes the n-dimensional sphere, RPn the n-dimensional real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
, and SU(n) the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
of degree n.
Homotopy groups
The homotopy groups of the orthogonal group are related to homotopy groups of spheresHomotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
, and thus are in general hard to compute.
However, one can compute the homotopy groups of the stable orthogonal group (aka the infinite orthogonal group), defined as the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of the sequence of inclusions
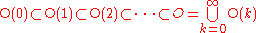
(as the inclusions are all closed inclusions, hence cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
s, this can also be interpreted as a union).
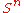 is a homogeneous space
is a homogeneous spaceHomogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
for
 , and one has the following fiber bundle
, and one has the following fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
:
which can be understood as "The orthogonal group
 acts transitively on the unit sphere
acts transitively on the unit sphere 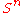 , and the stabilizer of a point (thought of as a unit vector) is the orthogonal group of the perpendicular complement, which is an orthogonal group one dimension lower". The map
, and the stabilizer of a point (thought of as a unit vector) is the orthogonal group of the perpendicular complement, which is an orthogonal group one dimension lower". The map  is the natural inclusion.
is the natural inclusion.Thus the inclusion
 is (n − 1)-connected
is (n − 1)-connectedN-connected
In the mathematical branch of algebraic topology, specifically homotopy theory, n-connectedness is a way to say that a space vanishes or that a map is an isomorphism "up to dimension n, in homotopy".-n-connected space:...
, so the homotopy groups stabilize, and
 for
for 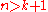 : thus the homotopy groups of the stable space equal the lower homotopy groups of the unstable spaces.
: thus the homotopy groups of the stable space equal the lower homotopy groups of the unstable spaces.Via Bott periodicity,
 , thus the homotopy groups of O are 8-fold periodic, meaning
, thus the homotopy groups of O are 8-fold periodic, meaning  , and one needs only to compute the lower 8 homotopy groups to compute them all.
, and one needs only to compute the lower 8 homotopy groups to compute them all.-
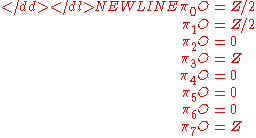
Relation to KO-theory
Via the clutching constructionClutching constructionIn topology, a branch of mathematics, the clutching construction is a way of constructing fiber bundles, particularly vector bundles on spheres.-Definition:...
, homotopy groups of the stable space O are identified with stable vector bundles on spheres (up to isomorphism), with a dimension shift of 1: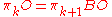 .
.
Setting (to make
(to make  fit into the periodicity), one obtains:
fit into the periodicity), one obtains:
-
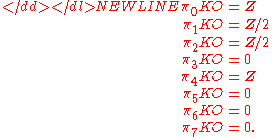
Low-dimensional groups
The first few homotopy groups can be calculated by using the concrete descriptions of low-dimensional groups.
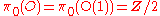 from orientationOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
from orientationOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
-preserving/reversing (this class survives to and hence stably)
and hence stably)
 yields
yields
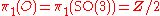 , which is spin
, which is spin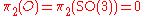 , which surjects onto
, which surjects onto  ; this latter thus vanishes.
; this latter thus vanishes.
Lie groups
From general facts about Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s,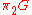 always vanishes, and
always vanishes, and 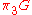 is free (free abelian).
is free (free abelian).
Vector bundles
From the vector bundle point of view,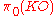 is vector bundles over
is vector bundles over 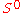 , which is two points. Thus over each point, the bundle is trivial, and the non-triviality of the bundle is the difference between the dimensions of the vector spaces over the two points, so
, which is two points. Thus over each point, the bundle is trivial, and the non-triviality of the bundle is the difference between the dimensions of the vector spaces over the two points, so is dimension.
is dimension.
Loop spaces
Using concrete descriptions of the loop spaces in Bott periodicity, one can interpret higher homotopy of O as lower homotopy of simple to analyze spaces. Using , O and O/U have two components,
, O and O/U have two components,  and
and 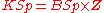 have
have  components, and the rest are connected.
components, and the rest are connected.
Interpretation of homotopy groups
In a nutshell: is dimension
is dimension is orientationOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
is orientationOrientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions... is spin
is spin is topological quantum field theoryTopological quantum field theoryA topological quantum field theory is a quantum field theory which computes topological invariants....
is topological quantum field theoryTopological quantum field theoryA topological quantum field theory is a quantum field theory which computes topological invariants....
.
Let , and let
, and let 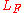 be the tautological line bundle over the projective line
be the tautological line bundle over the projective line 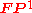 , and
, and 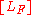 its class in K-theory. Noting that
its class in K-theory. Noting that 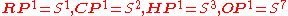 , these yield vector bundles over the corresponding spheres, and
, these yield vector bundles over the corresponding spheres, and
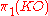 is generated by
is generated by 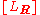
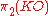 is generated by
is generated by 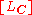
 is generated by
is generated by 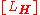
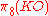 is generated by
is generated by 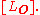
From the point of view of symplectic geometry,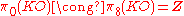 can be interpreted as the Maslov index, thinking of it as the fundamental group of the stable Lagrangian GrassmannianLagrangian GrassmannianIn mathematics, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space V. Its dimension is n/2 . It may be identified with the homogeneous space...
can be interpreted as the Maslov index, thinking of it as the fundamental group of the stable Lagrangian GrassmannianLagrangian GrassmannianIn mathematics, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space V. Its dimension is n/2 . It may be identified with the homogeneous space...
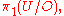 as
as  so
so 
Over finite fields
Orthogonal groups can also be defined over finite fields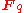 , where
, where  is a power of a prime
is a power of a prime 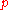 . When defined over such fields, they come in two types in even dimension:
. When defined over such fields, they come in two types in even dimension: 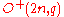 and
and 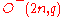 ; and one type in odd dimension:
; and one type in odd dimension:  .
.
If is the vector space on which the orthogonal group
is the vector space on which the orthogonal group  acts, it can be written as a direct orthogonal sum as follows:
acts, it can be written as a direct orthogonal sum as follows:
where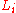 are hyperbolic lines and
are hyperbolic lines and  contains no singular vectors. If
contains no singular vectors. If  , then
, then  is of plus type. If
is of plus type. If  then
then  has odd dimension. If
has odd dimension. If  has dimension 2,
has dimension 2,  is of minus type.
is of minus type.
In the special case where n = 1,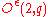 is a dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
is a dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order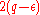 .
.
We have the following formulas for the order of these groups, O(n,q) = { A in GL(n,q) : A·At=I }, when the characteristic is greater than two
If −1 is a square in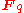
If −1 is a nonsquare in
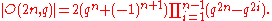
The Dickson invariant
For orthogonal groups, the Dickson invariant
is a homomorphism from the orthogonal group to Z/2Z, and is 0 or 1 depending on whether an element is the product of an even or odd number of reflections. More concretely, the Dickson invariant can be defined as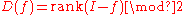 where I is the identity . Over fields that are not of characteristic 2 it is equivalent to the determinant: the determinant is −1 to the power of the Dickson invariant.
where I is the identity . Over fields that are not of characteristic 2 it is equivalent to the determinant: the determinant is −1 to the power of the Dickson invariant.
Over fields of characteristic 2, the determinant is always 1, so the Dickson invariant gives no extra information.
The special orthogonal group is the kernel of the Dickson invariant and usually has index 2 in O(n,F). When the characteristic of F is not 2, the Dickson Invariant is 0 whenever the determinant is 1. Thus when the characteristic is not 2, SO(n,F) is commonly defined to be the elements of O(n,F) with determinant 1. Each element in O(n,F) has determinant −1 or 1. Thus in characteristic 2, the determinant is always 1.
The Dickson invariant can also be defined for Clifford groups and Pin groupPin groupIn mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
s in a similar way (in all dimensions).
Orthogonal groups of characteristic 2
Over fields of characteristic 2 orthogonal groups often behave differently. This section lists some of the differences. Traditionally these groups are known as the hypoabelian groupHypoabelian group*"Hypoabelian group" is an archaic name for an orthogonal group over a field of characteristic 2.*A hypoabelian group can mean a group whose perfect core is trivial...
s but this term is no longer used for these groups.
- Any orthogonal group over any field is generated by reflections, except for a unique example where the vector space is 4 dimensional over the field with 2 elements and the Witt index is 2. Note that a reflection in characteristic two has a slightly different definition. In characteristic two, the reflection orthogonal to a vector u takes a vector v to v+B(v,u)/Q(u)·u where B is the bilinear form and Q is the quadratic form associated to the orthogonal geometry. Compare this to the Householder reflection of odd characteristic or characteristic zero, which takes v to v − 2·B(v,u)/Q(u)·u.
- The center of the orthogonal group usually has order 1 in characteristic 2, rather than 2, since

- In odd dimensions 2n+1 in characteristic 2, orthogonal groups over perfect fields are the same as symplectic groups in dimension 2n. In fact the symmetric form is alternating in characteristic 2, and as the dimension is odd it must have a kernel of dimension 1, and the quotient by this kernel is a symplectic space of dimension 2n, acted upon by the orthogonal group.
- In even dimensions in characteristic 2 the orthogonal group is a subgroup of the symplectic group, because the symmetric bilinear form of the quadratic form is also an alternating form.
The spinor norm
The spinor norm is a homomorphism from an orthogonal group over a field F to
- F*/F*2,
the multiplicative groupMultiplicative groupIn mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of the field F up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
square elements, that takes reflection in a vector of norm n to the image of n in F*/F*2.
For the usual orthogonal group over the reals it is trivial, but it is often non-trivial over other fields, or for the orthogonal group of a quadratic form over the reals that is not positive definite.
Galois cohomology and orthogonal groups
In the theory of Galois cohomologyGalois cohomologyIn mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
of algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s, some further points of view are introduced. They have explanatory value, in particular in relation with the theory of quadratic forms; but were for the most part post hoc, as far as the discovery of the phenomena is concerned. The first point is that quadratic formQuadratic formIn mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s over a field can be identified as a Galois H1, or twisted forms (torsors) of an orthogonal group. As an algebraic group, an orthogonal group is in general neither connected nor simply-connected; the latter point brings in the spin phenomena, while the former is related to the discriminantDiscriminantIn algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
.
The 'spin' name of the spinor norm can be explained by a connection to the spin group (more accurately a pin groupPin groupIn mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
). This may now be explained quickly by Galois cohomology (which however postdates the introduction of the term by more direct use of Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s). The spin covering of the orthogonal group provides a short exact sequence of algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s.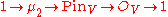
Here μ2 is the algebraic group of square roots of 1; over a field of characteristic not 2 it is roughly the same as a two-element group with trivial Galois action.
The connecting homomorphism from H0(OV), which is simply the group OV(F) of F-valued points, to H1(μ2) is essentially the spinor norm, because H1(μ2) is isomorphic to the multiplicative group of the field modulo squares.
There is also the connecting homomorphism from H1 of the orthogonal group, to the H2 of the kernel of the spin covering. The cohomology is non-abelian, so that this is as far as we can go, at least with the conventional definitions.
Related groups
The orthogonal groups and special orthogonal groups have a number of important subgroups, supergroups, quotient groups, and covering groups. These are listed below.
The inclusions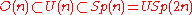 and
and  are part of a sequence of 8 inclusions used in a geometric proof of the Bott periodicity theorem, and the corresponding quotient spaces are symmetric spaceSymmetric spaceA symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
are part of a sequence of 8 inclusions used in a geometric proof of the Bott periodicity theorem, and the corresponding quotient spaces are symmetric spaceSymmetric spaceA symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
s of independent interest – for example, is the Lagrangian GrassmannianLagrangian GrassmannianIn mathematics, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space V. Its dimension is n/2 . It may be identified with the homogeneous space...
is the Lagrangian GrassmannianLagrangian GrassmannianIn mathematics, the Lagrangian Grassmannian is the smooth manifold of Lagrangian subspaces of a real symplectic vector space V. Its dimension is n/2 . It may be identified with the homogeneous space...
.
Lie subgroups
In physics, particularly in the areas of Kaluza–Klein compactification, it is important to find out the subgroups of the orthogonal group. The main ones are: – preserves an axis
– preserves an axis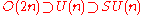 – U(n) are those that preserve a compatible complex structure or a compatible symplectic structure – see 2-out-of-3 property; SU(n) also preserves a complex orientation.
– U(n) are those that preserve a compatible complex structure or a compatible symplectic structure – see 2-out-of-3 property; SU(n) also preserves a complex orientation.
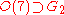
Lie supergroups
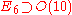
The orthogonal group O(n) is also an important subgroup of various Lie groups:


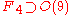


Discrete subgroups
As the orthogonal group is compact, discrete subgroups are equivalent to finite subgroups.Infinite subsets of a compact space have an accumulation point and are not discrete. These subgroups are known as point groupPoint groupIn geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
and can be realized as the symmetry groups of polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s. A very important class of examples are the finite Coxeter groups, which include the symmetry groups of regular polytopeRegular polytopeIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s.
Dimension 3 is particularly studied – see point groups in three dimensionsPoint groups in three dimensionsIn geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
, polyhedral groupPolyhedral groupIn geometry, the polyhedral group is any of the symmetry groups of the Platonic solids. There are three polyhedral groups:*The tetrahedral group of order 12, rotational symmetry group of the regular tetrahedron....
s, and list of spherical symmetry groups. In 2 dimensions, the finite groups are either cyclic or dihedral – see point groups in two dimensionsPoint groups in two dimensionsIn geometry, a two-dimensional point group or rosette group is a group of geometric symmetries that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O, including O itself...
.
Other finite subgroups include:- Permutation matrices (the Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
An) - Signed permutation matrices (the Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
Bn); also equals the intersection of the orthogonal group with the integer matrices.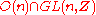 equals the signed permutation matrices because an integer vector of norm 1 must have a single non-zero entry, which must be ±1 (if it has two non-zero entries or a larger entry, the norm will be larger than 1), and in an orthogonal matrix these entries must be in different coordinates, which is exactly the signed permutation matrices.
equals the signed permutation matrices because an integer vector of norm 1 must have a single non-zero entry, which must be ±1 (if it has two non-zero entries or a larger entry, the norm will be larger than 1), and in an orthogonal matrix these entries must be in different coordinates, which is exactly the signed permutation matrices.
Covering and quotient groups
The orthogonal group is neither simply connected nor centerless, and thus has both a covering group and a quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
, respectively:- Two covering Pin groupPin groupIn mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
s, Pin+(n) → O(n) and Pin−(n) → O(n), - The quotient projective orthogonal groupProjective orthogonal groupIn projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space V = A quadratic space is a vector space V together with a quadratic form Q; the Q is dropped from notation when it is clear. on the associated projective...
, O(n) → PO(n).
These are all 2-to-1 covers.
For the special orthogonal group, the corresponding groups are:- Spin group, Spin(n) → SO(n),
- Projective special orthogonal group, SO(n) → PSO(n).
Spin is a 2-to-1 cover, while in even dimension, PSO(2k) is a 2-to-1 cover, and in odd dimension PSO(2k+1) is a 1-to-1 cover, i.e., isomorphic to SO(2k+1). These groups, Spin(n), SO(n), and PSO(n) are Lie group forms of the compact special orthogonal Lie algebra,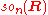 – Spin is the simply connected form, while PSO is the centerless form, and SO is in general neither.In odd dimension, SO(2k+1)
– Spin is the simply connected form, while PSO is the centerless form, and SO is in general neither.In odd dimension, SO(2k+1)  PSO(2k+1) is centerless (but not simply connected), while in even dimension SO(2k) is neither centerless nor simply connected.
PSO(2k+1) is centerless (but not simply connected), while in even dimension SO(2k) is neither centerless nor simply connected.
In dimension 3 and above these are the covers and quotients, while dimension 2 and below are somewhat degenerate; see specific articles for details.
Applications to string theory
The group O(10) is of special importance in superstring theorySuperstring theorySuperstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
because it is the symmetry group of 10 dimensional space-time.
Principal homogeneous space: Stiefel manifold
The principal homogeneous spacePrincipal homogeneous spaceIn mathematics, a principal homogeneous space, or torsor, for a group G is a homogeneous space X for G such that the stabilizer subgroup of any point is trivial...
for the orthogonal group O(n) is the Stiefel manifoldStiefel manifoldIn mathematics, the Stiefel manifold Vk is the set of all orthonormal k-frames in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel...
 of orthonormal bases (orthonormal n-framesK-frameIn linear algebra, a branch of mathematics, a k-frame is an ordered set of k linearly independent vectors in a space; thus k ≤ n, where n is the dimension of the vector space, and if k = n an n-frame is precisely an ordered basis.If the vectors are orthogonal, or orthonormal,...
of orthonormal bases (orthonormal n-framesK-frameIn linear algebra, a branch of mathematics, a k-frame is an ordered set of k linearly independent vectors in a space; thus k ≤ n, where n is the dimension of the vector space, and if k = n an n-frame is precisely an ordered basis.If the vectors are orthogonal, or orthonormal,...
).
In other words, the space of orthonormal bases is like the orthogonal group, but without a choice of base point: given an orthogonal space, there is no natural choice of orthonormal basis, but once one is given one, there is a one-to-one correspondence between bases and the orthogonal group.
Concretely, a linear map is determined by where it sends a basis: just as an invertible map can take any basis to any other basis, an orthogonal map can take any orthogonal basis to any other orthogonal basis.
The other Stiefel manifolds for
for  of incomplete orthonormal bases (orthonormal k-frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any k-frame can be taken to any other k-frame by an orthogonal map, but this map is not uniquely determined.
of incomplete orthonormal bases (orthonormal k-frames) are still homogeneous spaces for the orthogonal group, but not principal homogeneous spaces: any k-frame can be taken to any other k-frame by an orthogonal map, but this map is not uniquely determined.
Specific transforms
- Coordinate rotations and reflectionsCoordinate rotations and reflectionsIn geometry, 2D coordinate rotations and reflections are two kinds of Euclidean plane isometries which are related to one another.A rotation in the plane can be formed by composing a pair of reflections. First reflect a point P to its image P′ on the other side of line L1...
- Reflection through the origin
External links
-