
Alternating group
Encyclopedia
In mathematics
, an alternating group is the group
of even permutations of a finite set. The alternating group on the set {1,...,n} is called the alternating group of degree n, or the alternating group on n letters and denoted by An or Alt(n).
of the symmetric group
Sn with index
2 and has therefore n!
/2 elements. It is the kernel
of the signature group homomorphism
sgn : Sn → {1, −1} explained under symmetric group
.
The group An is abelian
if and only if
n ≤ 3 and simple
if and only if n = 3 or n ≥ 5. A5 is the smallest non-abelian simple group
, having order 60, and the smallest non-solvable group
.
The group A4 has a Klein four-group
V as a proper normal subgroup
, namely the double transpositions {(12)(34), (13)(24), (14)(23)}, and maps to , from the sequence
, from the sequence  In Galois theory
In Galois theory
, this map, or rather the corresponding map corresponds to associating the Lagrange resolvent cubic to a quartic, which allows the quartic polynomial to be solved by radicals, as established by Lodovico Ferrari
corresponds to associating the Lagrange resolvent cubic to a quartic, which allows the quartic polynomial to be solved by radicals, as established by Lodovico Ferrari
.
, the conjugacy class
es in An consist of elements with the same cycle shape. However, if the cycle shape consists only of cycles of odd length with no two cycles the same length, where cycles of length one are included in the cycle type, then there are exactly two conjugacy classes for this cycle shape .
Examples:
For n > 3, except for n = 6, the automorphism group of An is the symmetric group Sn, with inner automorphism group An and outer automorphism group
Z2; the outer automorphism comes from conjugation by an odd permutation.
For n = 1 and 2, the automorphism group is trivial. For n = 3 the automorphism group is Z2, with trivial inner automorphism group and outer automorphism group Z2.
The outer automorphism group of A6 is the Klein four-group
V = Z2 × Z2, and is related to the outer automorphism of S6. The extra outer automorphism in A6 swaps the 3-cycles (like (123)) with elements of shape 32 (like (123)(456)).
s between some of the small alternating groups and small groups of Lie type, particularly projective special linear groups. These are:
More obviously, A3 is isomorphic to the cyclic group
Z3, and A0, A1, and A2 are isomorphic to the trivial group
(which is also SL1(q)=PSL1(q) for any q).
is not true in general: given a finite group G and a divisor d of |G|, there does not necessarily exist a subgroup of G with order d: the group G = A4, of order 12, has no subgroup of order 6. A subgroup of three elements (generated by a cyclic rotation of three objects) with any additional element generates the whole group.
: for sufficiently large n, it is constant. However, there are some low dimensional exceptional homology. Note that the homology of the symmetric group exhibits similar stabilization, but without the low dimensional exceptions (additional homology elements).
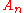 is perfect
is perfect
, except for the cited exceptions) is thus: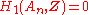 for
for 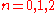 ;
; ;
;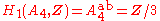 ;
;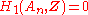 for
for  .
.
This is easily seen directly, as follows.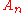 is generated by 3-cycles – so the only non-trivial abelianization maps are
is generated by 3-cycles – so the only non-trivial abelianization maps are  since order 3 elements must map to order 3 elements – and for
since order 3 elements must map to order 3 elements – and for  all 3-cycles are conjugate, so they must map to the same element in the abelianization, since conjugation is trivial in abelian groups. Thus a 3-cycle like (123) must map to the same element as its inverse (321), but thus must map to the identity, as it must then have order dividing 2 and 3, so the abelianization is trivial.
all 3-cycles are conjugate, so they must map to the same element in the abelianization, since conjugation is trivial in abelian groups. Thus a 3-cycle like (123) must map to the same element as its inverse (321), but thus must map to the identity, as it must then have order dividing 2 and 3, so the abelianization is trivial.
For
 is trivial, and thus has trivial abelianization. For
is trivial, and thus has trivial abelianization. For 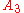 and
and  one can compute the abelianization directly, noting that the 3-cycles form two conjugacy classes (rather than all being conjugate) and there are non-trivial maps
one can compute the abelianization directly, noting that the 3-cycles form two conjugacy classes (rather than all being conjugate) and there are non-trivial maps  (in fact an isomorphism) and
(in fact an isomorphism) and 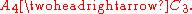
s of the alternating groups An (in the case where n is at least 5) are the cyclic groups of order 2, except in the case where n is either 6 or 7, in which case there is also a triple cover. In these cases, then, the Schur multiplier is (the cyclic group) of order 6. These were first computed in .
 for
for 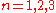 ;
;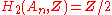 for
for  ;
;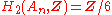 for
for  ;
;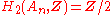 for
for  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an alternating group is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of even permutations of a finite set. The alternating group on the set {1,...,n} is called the alternating group of degree n, or the alternating group on n letters and denoted by An or Alt(n).
Basic properties
For n > 1, the group An is the commutator subgroupCommutator subgroup
In mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn with index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 and has therefore n!
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
/2 elements. It is the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the signature group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
sgn : Sn → {1, −1} explained under symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
.
The group An is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
n ≤ 3 and simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
if and only if n = 3 or n ≥ 5. A5 is the smallest non-abelian simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, having order 60, and the smallest non-solvable group
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
.
The group A4 has a Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
V as a proper normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, namely the double transpositions {(12)(34), (13)(24), (14)(23)}, and maps to
 , from the sequence
, from the sequence  In Galois theory
In Galois theoryGalois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, this map, or rather the corresponding map
 corresponds to associating the Lagrange resolvent cubic to a quartic, which allows the quartic polynomial to be solved by radicals, as established by Lodovico Ferrari
corresponds to associating the Lagrange resolvent cubic to a quartic, which allows the quartic polynomial to be solved by radicals, as established by Lodovico FerrariLodovico Ferrari
Lodovico Ferrari was an Italian mathematician.Born in Milan, Italy, grandfather, Bartholomew Ferrari was forced out of Milan to Bologna. He settled in Bologna, Italy and he began his career as the servant of Gerolamo Cardano. He was extremely bright, so Cardano started teaching him mathematics...
.
Conjugacy classes
As in the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, the conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es in An consist of elements with the same cycle shape. However, if the cycle shape consists only of cycles of odd length with no two cycles the same length, where cycles of length one are included in the cycle type, then there are exactly two conjugacy classes for this cycle shape .
Examples:
- the two permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s (123) and (132) are not conjugates in A3, although they have the same cycle shape, and are therefore conjugate in S3 - the permutation (123)(45678) is not conjugate to its inverse (132)(48765) in A8, although the two permutations have the same cycle shape, so they are conjugate in S8.
Automorphism group
 |
 |
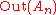 |
 |
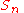 |
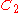 |
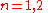 |
 |
 |
 |
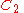 |
 |
 |
 |
 |
For n > 3, except for n = 6, the automorphism group of An is the symmetric group Sn, with inner automorphism group An and outer automorphism group
Outer automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
Z2; the outer automorphism comes from conjugation by an odd permutation.
For n = 1 and 2, the automorphism group is trivial. For n = 3 the automorphism group is Z2, with trivial inner automorphism group and outer automorphism group Z2.
The outer automorphism group of A6 is the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
V = Z2 × Z2, and is related to the outer automorphism of S6. The extra outer automorphism in A6 swaps the 3-cycles (like (123)) with elements of shape 32 (like (123)(456)).
Exceptional isomorphisms
There are some exceptional isomorphismExceptional isomorphism
In mathematics, an exceptional isomorphism, also called an accidental isomorphism, is an isomorphism between members ai and bj of two families of mathematical objects, that is not an example of a pattern of such isomorphisms.Because these series of objects are presented differently, they are not...
s between some of the small alternating groups and small groups of Lie type, particularly projective special linear groups. These are:
- A4 is isomorphic to PSL2(3) and the symmetry groupSymmetry groupThe symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of chiral tetrahedral symmetryTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
. - A5 is isomorphic to PSL2(4), PSL2(5), and the symmetry group of chiral icosahedral symmetryIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
.(See for an indirect isomorphism of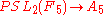 using a classification of simple groups of order 60, and here for a direct proof).
using a classification of simple groups of order 60, and here for a direct proof). - A6 is isomorphic to PSL2(9) and PSp4(2)'
- A8 is isomorphic to PSL4(2)
More obviously, A3 is isomorphic to the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z3, and A0, A1, and A2 are isomorphic to the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
(which is also SL1(q)=PSL1(q) for any q).
Examples S4 and A4
Subgroups
A4 is the smallest group demonstrating that the converse of Lagrange's theoremLagrange's theorem (group theory)
Lagrange's theorem, in the mathematics of group theory, states that for any finite group G, the order of every subgroup H of G divides the order of G. The theorem is named after Joseph Lagrange....
is not true in general: given a finite group G and a divisor d of |G|, there does not necessarily exist a subgroup of G with order d: the group G = A4, of order 12, has no subgroup of order 6. A subgroup of three elements (generated by a cyclic rotation of three objects) with any additional element generates the whole group.
Group homology
The group homology of the alternating groups exhibits stabilization, as in stable homotopy theoryStable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
: for sufficiently large n, it is constant. However, there are some low dimensional exceptional homology. Note that the homology of the symmetric group exhibits similar stabilization, but without the low dimensional exceptions (additional homology elements).
H1: Abelianization
The first homology group coincides with abelianization, and (since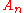 is perfect
is perfectPerfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
, except for the cited exceptions) is thus:
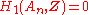 for
for 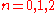 ;
; ;
;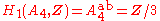 ;
;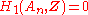 for
for  .
.This is easily seen directly, as follows.
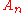 is generated by 3-cycles – so the only non-trivial abelianization maps are
is generated by 3-cycles – so the only non-trivial abelianization maps are  since order 3 elements must map to order 3 elements – and for
since order 3 elements must map to order 3 elements – and for  all 3-cycles are conjugate, so they must map to the same element in the abelianization, since conjugation is trivial in abelian groups. Thus a 3-cycle like (123) must map to the same element as its inverse (321), but thus must map to the identity, as it must then have order dividing 2 and 3, so the abelianization is trivial.
all 3-cycles are conjugate, so they must map to the same element in the abelianization, since conjugation is trivial in abelian groups. Thus a 3-cycle like (123) must map to the same element as its inverse (321), but thus must map to the identity, as it must then have order dividing 2 and 3, so the abelianization is trivial.For

 is trivial, and thus has trivial abelianization. For
is trivial, and thus has trivial abelianization. For 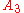 and
and  one can compute the abelianization directly, noting that the 3-cycles form two conjugacy classes (rather than all being conjugate) and there are non-trivial maps
one can compute the abelianization directly, noting that the 3-cycles form two conjugacy classes (rather than all being conjugate) and there are non-trivial maps  (in fact an isomorphism) and
(in fact an isomorphism) and 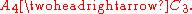
H2: Schur multipliers
The Schur multiplierSchur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
s of the alternating groups An (in the case where n is at least 5) are the cyclic groups of order 2, except in the case where n is either 6 or 7, in which case there is also a triple cover. In these cases, then, the Schur multiplier is (the cyclic group) of order 6. These were first computed in .
 for
for 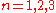 ;
;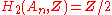 for
for  ;
;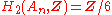 for
for  ;
;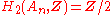 for
for  .
.

