
Icosahedral symmetry
Encyclopedia

Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
has 60 rotational (or orientation-preserving) symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation. A regular dodecahedron has the same set of symmetries, since it is the dual of the icosahedron.
The set of orientation-preserving symmetries forms a group referred to as A5 (the alternating group on 5 letters), and the full symmetry group (including reflections) is the product A5 × C2. The latter group is also known as the Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
H3.
As point group
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
(or equivalently, symmetries on the sphere) with the largest symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s.
Icosahedral symmetry is not compatible with translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
, so there are no associated crystallographic point groups or space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s.
| Schönflies Arthur Moritz Schönflies Arthur Moritz Schoenflies , sometimes written as Schönflies, was a German mathematician, known for his contributions to the application of group theory to crystallography, and for work in topology.... crystallographic notation |
Coxeter notation Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M... |
Orbifold notation |
Order |
|---|---|---|---|
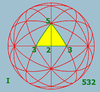
| I | [3,5]+ | 532 | 60 |
| Ih | [3,5] | *532 | 120 |
Presentations
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
corresponding to the above are:
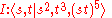
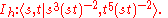
These correspond to the icosahedral groups (rotational and full) being the (2,3,5) triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
s.
The first presentation was given by William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1856, in his paper on Icosian Calculus
Icosian Calculus
The Icosian Calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856.In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations....
.
Note that other presentations are possible, for instance as an alternating group (for I).
Group structure
The icosahedral rotation group I is of order 60. The group I is isomorphic to A5, the alternating group of even permutations of five objects. This isomorphism can be realized by I acting on various compounds, notably the compound of five cubesCompound of five cubes
This polyhedral compound is a symmetric arrangement of five cubes. This compound was first described by Edmund Hess in 1876.It is one of five regular compounds, and dual to the compound of five octahedra....
(which inscribe in the dodecahedron), the compound of five octahedra
Compound of five octahedra
This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23....
, or either of the two compounds of five tetrahedra
Compound of five tetrahedra
This compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.-As a compound:It can be constructed by arranging five tetrahedra in rotational icosahedral symmetry , as colored in the upper right model...
(which are enantiomorphs, and inscribe in the dodecahedron).
The group contains 5 versions of Th with 20 versions of D3 (10 axes, 2 per axis), and 6 versions of D5.
The Ih has order 120. It has I as normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2. The group Ih is isomorphic to I × C2, or A5 × C2, with the inversion in the center corresponding to element (identity,-1), where C2 is written multiplicatively.
Ih acts on the compound of five cubes
Compound of five cubes
This polyhedral compound is a symmetric arrangement of five cubes. This compound was first described by Edmund Hess in 1876.It is one of five regular compounds, and dual to the compound of five octahedra....
and the compound of five octahedra
Compound of five octahedra
This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23....
, but -1 acts as the identity (as cubes and octahedra are centrally symmetric). It acts on the compound of ten tetrahedra
Compound of ten tetrahedra
This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a compound :It can also be seen as the compound of ten tetrahedra with full icosahedral symmetry...
: I acts on the two chiral halves (compounds of five tetrahedra
Compound of five tetrahedra
This compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.-As a compound:It can be constructed by arranging five tetrahedra in rotational icosahedral symmetry , as colored in the upper right model...
), and -1 interchanges the two halves.
Notably, it does not act as S5, and these groups are not isomorphic; see below for details.
The group contains 10 versions of D3d and 6 versions of D5d (symmetries like antiprisms).
I is also isomorphic to PSL2(5), but Ih is not isomorphic to SL2(5).
Commonly confused groups
The following groups all have order 120, but are not isomorphic:- S5, the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 5 elements - Ih, the full icosahedral group (subject of this article, also known as H3)
- 2I, the binary icosahedral group
They correspond to the following short exact sequences (which do not split) and product
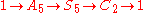
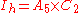
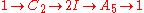
In words,
-
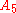 is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of
-
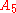 is a factor of
is a factor of 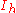 , which is a direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
, which is a direct productDirect product of groupsIn the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted... -
 is a quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
is a quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of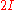
Note that
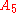 has an exceptional
has an exceptionalExceptional object
Many branches of mathematics study objects of a given type and prove a classification theorem. A common theme is that the classification results in a number of series of objects as well as a finite number of exceptions that don't fit into any series. These are known as exceptional...
irreducible 3-dimensional representation (as the icosahedral rotation group), but
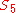 does not have an irreducible 3-dimensional representation, corresponding to the full icosahedral group not being the symmetric group.
does not have an irreducible 3-dimensional representation, corresponding to the full icosahedral group not being the symmetric group.These can also be related to linear groups over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with five elements, which exhibit the subgroups and covering groups directly; none of these are the full icosahedral group:
-
 the projective special linear group, see here for a proof;
the projective special linear group, see here for a proof; -
 the projective general linear group;
the projective general linear group; -
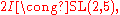 the special linear groupSpecial linear groupIn mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
the special linear groupSpecial linear groupIn mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
.
Conjugacy classes
The conjugacy classConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es of I are:
- identity
- 12 × rotation by 72°, order 5
- 12 × rotation by 144°, order 5
- 20 × rotation by 120°, order 3
- 15 × rotation by 180°, order 2
Those of Ih include also each with inversion:
- inversion
- 12 × rotoreflection by 108°, order 10
- 12 × rotoreflection by 36°, order 10
- 20 × rotoreflection by 60°, order 6
- 15 × reflection, order 2
Subgroups
- Ih,I , Th and T
- D2h
- D5d, D3d
- D5, D3 and D2
- C2h
- C5v, C3v and C2v
- C5, C3 and C2
- S10, S6 and S2=Ci
- E and Cs
All of these classes of subgroups are conjugate (i.e., all vertex stabilizers are conjugate), and admit geometric interpretations.
Note that the stabilizer of a vertex/edge/face/polyhedron and its opposite are equal, since
 is central.
is central.Vertex stabilizers
Stabilizers of an opposite pair of vertices can be interpreted as stabilizers of the axis they generate.- vertex stabilizers in I give cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s C3 - vertex stabilizers in Ih give dihedral groupsDihedral symmetry in three dimensionsThis article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
D3 - stabilizers of an opposite pair of vertices in I give dihedral groups D3
- stabilizers of an opposite pair of vertices in Ih give
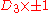
Edge stabilizers
Stabilizers of an opposite pair of edges can be interpreted as stabilizers of the rectangle they generate.- edges stabilizers in I give cyclic groups C2
- edges stabilizers in Ih give Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
s
- stabilizers of a pair of edges in I give Klein four-groupKlein four-groupIn mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
s ; there are 5 of these, given by rotation by 180° in 3 perpendicular axes.
; there are 5 of these, given by rotation by 180° in 3 perpendicular axes. - stabilizers of a pair of edges in Ih give
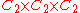 ; these are 5 of these, given by reflections in 3 perpendicular axes.
; these are 5 of these, given by reflections in 3 perpendicular axes.
Face stabilizers
Stabilizers of an opposite pair of faces can be interpreted as stabilizers of the anti-prism they generate.- face stabilizers in I give cyclic groups C5
- face stabilizers in Ih give dihedral groups D5
- stabilizers of an opposite pair of faces in I give dihedral groups D5
- stabilizers of an opposite pair of faces in Ih give

Polyhedron stabilizers
For each of these, there are 5 conjugate copies, and the conjugation action gives a map, indeed an isomorphism, .
.
- stabilizers of the inscribed tetrahedra in I are a copy of T
- stabilizers of the inscribed tetrahedra in Ih are a copy of Th
- stabilizers of the inscribed cubes (or opposite pair of tetrahedra, or octahedrons) in I are a copy of O
- stabilizers of the inscribed cubes (or opposite pair of tetrahedra, or octahedrons) in Ih are a copy of Oh
Fundamental domain
Fundamental domains for the icosahedral rotation group and the full icosahedral group are given by: | 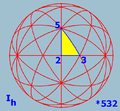 |

Disdyakis triacontahedron
In geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons...
one full face is a fundamental domain; other solids with the same symmetry can be obtained by adjusting the orientation of the faces, e.g. flattening selected subsets of faces to combine each subset into one face, or replacing each face by multiple faces, or a curved surface.
Full icosahedral symmetry
Platonic solidPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s - regular polyhedra (all faces of the same type)
 {5,3} |  {3,5} |
Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s - polyhedra with more than one polygon face type.
 3.10.10 |  4.6.10 |  5.6.6 |  3.4.5.4 |  3.5.3.5 |
Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s - duals of the Archimedean solids.
 V3.10.10 |  V4.6.10 |  V5.6.6 |  V3.4.5.4 |  V3.5.3.5 |
Other objects with icosahedral symmetry
- Barth surfaceBarth surfaceIn algebraic geometry, a Barth surface is one of the complex surfaces in 3 dimensions with large numbers of double points found by . Two examples are the Barth sextic of degree 6 with 65 double points, and the Barth decic of degree 10 with 345 double points.Some admit icosahedral symmetry.-External...
s - Virus structure, and CapsidCapsidA capsid is the protein shell of a virus. It consists of several oligomeric structural subunits made of protein called protomers. The observable 3-dimensional morphological subunits, which may or may not correspond to individual proteins, are called capsomeres. The capsid encloses the genetic...
Liquid Crystals with icosahedral symmetry
For the intermediate material phase called Liquid Crystalsthe existence of icosahedral symmetry was proposed
by
H. Kleinert
Hagen Kleinert
Hagen Kleinert is Professor of Theoretical Physics at the Free University of Berlin, Germany , at theWest University of Timişoara, at thein Bishkek. He is also of the...
and K. Maki
and its structure was first analyzed in detail in that paper. See the review article here.
In aluminum, the icohahedral structure was discovered experimentally three years after this
by Dan Shechtman
Dan Shechtman
Dan Shechtman is the Philip Tobias Professor of Materials Science at the Technion – Israel Institute of Technology, an Associate of the US Department of Energy's Ames Laboratory, and Professor of Materials Science at Iowa State University. On April 8, 1982, while on sabbatical at the U.S...
, which earned him the Nobel Prize in 2011.
Related geometries
Icosahedral symmetry is equivalently the projective special linear group PSL(2,5), and is the symmetry group of the modular curveModular curve
In number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
X(5), and more generally PSL(2,p) is the symmetry group of the modular curve X(p). The modular curve X(5) is geometrically a dodecahedron with a cusp at the center of each polygonal face, which demonstrates the symmetry group.
This geometry, and associated symmetry group, was studied by Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
as the monodromy groups of a Belyi surface – a Riemann surface with a holomorphic map to the Riemann sphere, ramified only at 0, 1, and infinity (a Belyi function) – the cusps are the points lying over infinity, while the vertices and the centers of each edge lie over 0 and 1; the degree of the covering (number of sheets) equals 5.
This arose from his efforts to give a geometric setting for why icosahedral symmetry arose in the solution of the quintic equation
Quintic equation
In mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
, with the theory given in the famous ; a modern exposition is given in .
Klein's investigations continued with his discovery of order 7 and order 11 symmetries in and (and associated coverings of degree 7 and 11) and dessins d'enfants, the first yielding the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
, whose associated geometry has a tiling by 24 heptagons (with a cusp at the center of each).
Similar geometries occur for PSL(2,n) and more general groups for other modular curves.
More exotically, there are special connections between the groups PSL(2,5) (order 60), PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
(order 168) and PSL(2,11) (order 660), which also admit geometric interpretations – PSL(2,5) is the symmetries of the icosahedron (genus 0), PSL(2,7) of the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
(genus 3), and PSL(2,11) the buckyball surface (genus 70). These groups form a "trinity" in the sense of Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
, which gives a framework for the various relationships; see trinities for details.
There is a close relationship to other Platonic Solids.
See also
- tetrahedral symmetryTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
- octahedral symmetryOctahedral symmetry150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
- binary icosahedral group
- Icosian CalculusIcosian CalculusThe Icosian Calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856.In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations....

