
Mayer-Vietoris sequence
Encyclopedia
In mathematics
, particularly algebraic topology
and homology theory
, the Mayer–Vietoris sequence is an algebra
ic tool to help compute algebraic invariants of topological space
s, known as their homology and cohomology groups. The result is due to two Austria
n mathematicians, Walther Mayer
and Leopold Vietoris
. The method consists of splitting a space into pieces, called subspaces
, for which the homology or cohomology groups may be easier to compute. The sequence relates the (co)homology groups of the space to the (co)homology groups of the subspaces. It is a natural long exact sequence, whose entries are the (co)homology groups of the whole space, the direct sum of the (co)homology groups of the subspaces, and the (co)homology groups of the intersection
of the subspaces.
The Mayer–Vietoris sequence holds for a variety of cohomology and homology theories
, including singular homology
and singular cohomology. In general, the sequence holds for those theories satisfying the Eilenberg-Steenrod axioms
, and it has variations for both reduced
and relative
(co)homology. Because the (co)homology of most spaces cannot be computed directly from their definitions, one uses tools such as the Mayer–Vietoris sequence in the hope of obtaining partial information. Many spaces encountered in topology
are constructed by piecing together very simple patches. Carefully choosing the two covering subspaces so that, together with their intersection, they have simpler (co)homology than that of the whole space may allow a complete deduction of the (co)homology of the space. In that respect, the Mayer–Vietoris sequence is analogous to the Seifert–van Kampen theorem
for the fundamental group
, and a precise relation exists for homology of dimension one.
 Like the fundamental group
Like the fundamental group
or the higher homotopy group
s of a space, homology groups are important topological invariants. Although some (co)homology theories are computable using tools of linear algebra
, many other important (co)homology theories, especially singular (co)homology, are not computable directly from their definition for nontrivial spaces. For singular (co)homology, the singular (co)chains and (co)cycles groups are often too big to handle directly. More subtle and indirect approaches become necessary. The Mayer–Vietoris sequence is such an approach, giving partial information about the (co)homology groups of any space by relating it to the (co)homology groups of two of its subspaces and their intersection.
The most natural and convenient way to express the relation involves the algebraic concept of exact sequence
s: sequences of objects (in this case groups
) and morphism
s (in this case group homomorphism
s) between them such that the image
of one morphism equals the kernel
of the next. In general, this does not allow (co)homology groups of a space to be completely computed. However, because many important spaces encountered in topology are topological manifold
s, simplicial complex
es, or CW complex
es, which are constructed by piecing together very simple patches, a theorem such as that of Mayer and Vietoris is potentially of broad and deep applicability.
Mayer was introduced to topology by his colleague Vietoris when attending his lectures in 1926 and 1927 at a local university in Vienna
. He was told about the conjectured result and a way to its solution, and solved the question for the Betti number
s in 1929. He applied his results to the torus
considered as the union of two cylinders. Vietoris later proved the full result for the homology groups in 1930 but did not express it as an exact sequence. The concept of an exact sequence only appeared in print in the 1952 book Foundations of Algebraic Topology by Samuel Eilenberg
and Norman Steenrod
where the results of Mayer and Vietoris were expressed in the modern form.
and A, B be two subspaces whose interiors
cover X. (The interiors of A and B need not be disjoint.) The Mayer–Vietoris sequence in singular homology
for the triad (X, A, B) is a long exact sequence relating the singular homology groups (with coefficient group the integers Z) of the spaces X, A, B, and the intersection
A∩B. There is an unreduced and a reduced version.
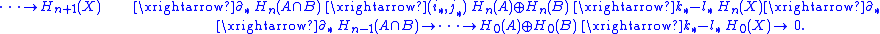
Here the maps i : A∩B ↪ A, j : A∩B ↪ B, k : A ↪ X, and l : B ↪ X are inclusion map
s and denotes the direct sum of abelian groups.
denotes the direct sum of abelian groups.
for example, can be written as the sum of two n-chains u and v whose images lie wholly in A and B, respectively. Thus ∂x = ∂(u + v) = 0 so that ∂u = −∂v. This implies that the images of both these boundary (n − 1)-cycles are contained in the intersection A∩B. Then ∂*([x]) is the class of ∂u in Hn−1(A∩B). Choosing a different representative x′ does not affect ∂u since ∂x′ = ∂x = 0; nor does choosing another decomposition x = u′ + v′ since then ∂u + ∂v − ∂u′ − ∂v′ = 0 which implies ∂u = ∂u′ and ∂v = ∂v′. Notice that the maps in the Mayer–Vietoris sequence depend on choosing an order for A and B. In particular, the boundary map changes sign if A and B are swapped.
there is also a Mayer–Vietoris sequence, under the assumption that A and B have non-empty intersection. The sequence is identical for positive dimensions and ends as:

. Whenever A∩B is path-connected the reduced Mayer–Vietoris sequence yields the isomorphism
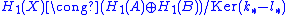
where, by exactness,
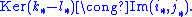
This is precisely the abelianized statement of the Seifert–van Kampen theorem. Compare with the fact that H1(X) is the abelianization of the fundamental group
π1(X) when X is path-connected.
. The Mayer–Vietoris sequence for reduced homology
groups then yields
Exactness immediately implies that the map ∂* is an isomorphism. Using the reduced homology
of the 0-sphere (two points) as a base case
, it follows
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
, the Mayer–Vietoris sequence is an algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic tool to help compute algebraic invariants of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, known as their homology and cohomology groups. The result is due to two Austria
Austria
Austria , officially the Republic of Austria , is a landlocked country of roughly 8.4 million people in Central Europe. It is bordered by the Czech Republic and Germany to the north, Slovakia and Hungary to the east, Slovenia and Italy to the south, and Switzerland and Liechtenstein to the...
n mathematicians, Walther Mayer
Walther Mayer
Walter Mayer was an Austrian mathematician, born 1887 in Graz, Austria.Mayer, who was Jewish, studied at the Federal Institute of Technology in Zürich and the University of Paris before receiving his doctorate in 1912 from the University of Vienna...
and Leopold Vietoris
Leopold Vietoris
Leopold Vietoris was an Austrian mathematician and a World War I veteran who gained additional fame by becoming a supercentenarian...
. The method consists of splitting a space into pieces, called subspaces
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
, for which the homology or cohomology groups may be easier to compute. The sequence relates the (co)homology groups of the space to the (co)homology groups of the subspaces. It is a natural long exact sequence, whose entries are the (co)homology groups of the whole space, the direct sum of the (co)homology groups of the subspaces, and the (co)homology groups of the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the subspaces.
The Mayer–Vietoris sequence holds for a variety of cohomology and homology theories
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
, including singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
and singular cohomology. In general, the sequence holds for those theories satisfying the Eilenberg-Steenrod axioms
Eilenberg-Steenrod axioms
In mathematics, specifically in algebraic topology, the Eilenberg–Steenrod axioms are properties that homology theories of topological spaces have in common...
, and it has variations for both reduced
Reduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
and relative
Relative homology
In algebraic topology, a branch of mathematics, the homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways...
(co)homology. Because the (co)homology of most spaces cannot be computed directly from their definitions, one uses tools such as the Mayer–Vietoris sequence in the hope of obtaining partial information. Many spaces encountered in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
are constructed by piecing together very simple patches. Carefully choosing the two covering subspaces so that, together with their intersection, they have simpler (co)homology than that of the whole space may allow a complete deduction of the (co)homology of the space. In that respect, the Mayer–Vietoris sequence is analogous to the Seifert–van Kampen theorem
Seifert–van Kampen theorem
In mathematics, the Seifert-van Kampen theorem of algebraic topology, sometimes just called van Kampen's theorem, expresses the structure of the fundamental group of a topological space X, in terms of the fundamental groups of two open, path-connected subspaces U and V that cover X...
for the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, and a precise relation exists for homology of dimension one.
Background, motivation, and history

Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
or the higher homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of a space, homology groups are important topological invariants. Although some (co)homology theories are computable using tools of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, many other important (co)homology theories, especially singular (co)homology, are not computable directly from their definition for nontrivial spaces. For singular (co)homology, the singular (co)chains and (co)cycles groups are often too big to handle directly. More subtle and indirect approaches become necessary. The Mayer–Vietoris sequence is such an approach, giving partial information about the (co)homology groups of any space by relating it to the (co)homology groups of two of its subspaces and their intersection.
The most natural and convenient way to express the relation involves the algebraic concept of exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
s: sequences of objects (in this case groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
) and morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s (in this case group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s) between them such that the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of one morphism equals the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the next. In general, this does not allow (co)homology groups of a space to be completely computed. However, because many important spaces encountered in topology are topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
s, simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
es, or CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es, which are constructed by piecing together very simple patches, a theorem such as that of Mayer and Vietoris is potentially of broad and deep applicability.
Mayer was introduced to topology by his colleague Vietoris when attending his lectures in 1926 and 1927 at a local university in Vienna
Vienna
Vienna is the capital and largest city of the Republic of Austria and one of the nine states of Austria. Vienna is Austria's primary city, with a population of about 1.723 million , and is by far the largest city in Austria, as well as its cultural, economic, and political centre...
. He was told about the conjectured result and a way to its solution, and solved the question for the Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s in 1929. He applied his results to the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
considered as the union of two cylinders. Vietoris later proved the full result for the homology groups in 1930 but did not express it as an exact sequence. The concept of an exact sequence only appeared in print in the 1952 book Foundations of Algebraic Topology by Samuel Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
and Norman Steenrod
Norman Steenrod
Norman Earl Steenrod was a preeminent mathematician most widely known for his contributions to the field of algebraic topology.-Life:...
where the results of Mayer and Vietoris were expressed in the modern form.
Basic versions for singular homology
Let X be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and A, B be two subspaces whose interiors
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
cover X. (The interiors of A and B need not be disjoint.) The Mayer–Vietoris sequence in singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
for the triad (X, A, B) is a long exact sequence relating the singular homology groups (with coefficient group the integers Z) of the spaces X, A, B, and the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
A∩B. There is an unreduced and a reduced version.
Unreduced version
For unreduced homology, the Mayer–Vietoris sequence states that the following sequence is exact: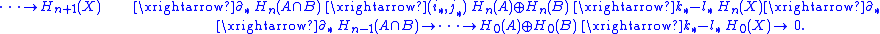
Here the maps i : A∩B ↪ A, j : A∩B ↪ B, k : A ↪ X, and l : B ↪ X are inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
s and
 denotes the direct sum of abelian groups.
denotes the direct sum of abelian groups.Boundary map
The boundary maps ∂* lowering the dimension may be made explicit as follows. An element in Hn(X) is the homology class of an n-cycle x which, by barycentric subdivisionBarycentric subdivision
In geometry, the barycentric subdivision is a standard way of dividing an arbitrary convex polygon into triangles, a convex polyhedron into tetrahedra, or, in general, a convex polytope into simplices with the same dimension, by connecting the barycenters of their faces in a specific way.The name...
for example, can be written as the sum of two n-chains u and v whose images lie wholly in A and B, respectively. Thus ∂x = ∂(u + v) = 0 so that ∂u = −∂v. This implies that the images of both these boundary (n − 1)-cycles are contained in the intersection A∩B. Then ∂*([x]) is the class of ∂u in Hn−1(A∩B). Choosing a different representative x′ does not affect ∂u since ∂x′ = ∂x = 0; nor does choosing another decomposition x = u′ + v′ since then ∂u + ∂v − ∂u′ − ∂v′ = 0 which implies ∂u = ∂u′ and ∂v = ∂v′. Notice that the maps in the Mayer–Vietoris sequence depend on choosing an order for A and B. In particular, the boundary map changes sign if A and B are swapped.
Reduced version
For reduced homologyReduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
there is also a Mayer–Vietoris sequence, under the assumption that A and B have non-empty intersection. The sequence is identical for positive dimensions and ends as:

Analogy with the Seifert–van Kampen theorem
There is an analogy between the Mayer–Vietoris sequence (especially for homology groups of dimension 1) and the Seifert–van Kampen theoremSeifert–van Kampen theorem
In mathematics, the Seifert-van Kampen theorem of algebraic topology, sometimes just called van Kampen's theorem, expresses the structure of the fundamental group of a topological space X, in terms of the fundamental groups of two open, path-connected subspaces U and V that cover X...
. Whenever A∩B is path-connected the reduced Mayer–Vietoris sequence yields the isomorphism
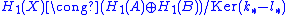
where, by exactness,
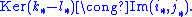
This is precisely the abelianized statement of the Seifert–van Kampen theorem. Compare with the fact that H1(X) is the abelianization of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
π1(X) when X is path-connected.
k-sphere
To completely compute the homology of the k-sphere X = Sk, let A and B be two hemispheres of X with intersection homotopic to a (k − 1)-dimensional equatorial sphere. Since the k-dimensional hemispheres are homeomorphic to k-discs, which are contractible, the homology groups for A and B are trivialTrivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
. The Mayer–Vietoris sequence for reduced homology
Reduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
groups then yields
Exactness immediately implies that the map ∂* is an isomorphism. Using the reduced homology
Reduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
of the 0-sphere (two points) as a base case
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, it follows
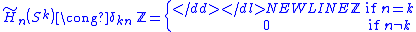
where δ is the Kronecker delta. Such a complete understanding of the homology groups for spheres is in stark contrast with current knowledge of homotopy groups of spheresHomotopy groups of spheresIn the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
, especially for the case n > k about which little is known.
Klein bottle
A slightly more difficult application of the Mayer–Vietoris sequence is the calculation of the homology groups of the Klein bottleKlein bottleIn mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
X. One uses the decomposition of X as the union of two Möbius stripMöbius stripThe Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
s A and B gluedQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
along their boundary circle (see illustration on the right). Then A, B and their intersection A∩B are homotopy equivalent to circles, so the nontrivial part of the sequence yields
and the trivial part implies vanishing homology for dimensions greater than 2. The central map α sends 1 to (2, −2) since the boundary circle of a Möbius band wraps twice around the core circle. In particular α is injectiveInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
so homology of dimension 2 also vanishes. Finally, choosing (1, 0) and (1, −1) as a basis for Z2, it follows
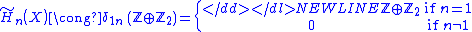
Wedge sums
Let X be the wedge sumWedge sumIn topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of two spaces K and L, and suppose furthermore that the identified basepoint is a deformation retractDeformation retractIn topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
of open neighborhoodsNeighbourhood (mathematics)In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
U ⊂ K and V ⊂ L. Letting A = K∪V and B = U∪L it follows that A∪B = X and A∩B = U∪V, which is contractible by construction. The reduced version of the sequence then yields (by exactness)
for all dimensions n. The illustration on the right shows X as the sum of two 2-spheres K and L. For this specific case, using the result from above for 2-spheres, one has
Suspensions
If X is the suspension SY of a space Y, let A and B be the complementsComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
in X of the top and bottom 'vertices' of the double cone, respectively. Then X is the union A∪B, with A and B contractible. Also, the intersection A∩B is homotopy equivalent to Y. Hence the Mayer–Vietoris sequence yields, for all n,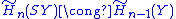
The illustration on the right shows the 1-sphere X as the suspension of the 0-sphere Y. Noting in general that the k-sphere is the suspension of the (k − 1)-sphere, it is easy to derive the homology groups of the k-sphere by induction, as above.
Relative form
A relativeRelative homologyIn algebraic topology, a branch of mathematics, the homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways...
form of the Mayer–Vietoris sequence also exists. If Y ⊂ X and is the union of C ⊂ A and D ⊂ B, then the exact sequence is:
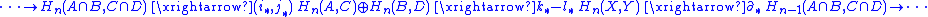
Naturality
The homology groups are natural in the sense that if ƒ is a continuous map from X1 to X2, then there is a canonical pushforward map ƒ∗ of homology groups ƒ∗ : Hk(X1) → Hk(X2), such that the composition of pushforwards is the pushforward of a composition: that is,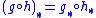 . The Mayer–Vietoris sequence is also natural in the sense that if X1 = A1∪B1 to X2 = A2∪B2 and the mapping ƒ satisfies ƒ(A1) ⊂ A2 and ƒ(B1) ⊂ B2, then the connecting morphism ∂∗ of the Mayer–Vietoris sequence commutes with ƒ∗. That is, the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
. The Mayer–Vietoris sequence is also natural in the sense that if X1 = A1∪B1 to X2 = A2∪B2 and the mapping ƒ satisfies ƒ(A1) ⊂ A2 and ƒ(B1) ⊂ B2, then the connecting morphism ∂∗ of the Mayer–Vietoris sequence commutes with ƒ∗. That is, the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
(the horizontal maps are the usual ones):
Cohomological versions
The Mayer–Vietoris long exact sequence for singular cohomology groups with coefficient groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is dualDuality (mathematics)In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
to the homological version. It is the following:
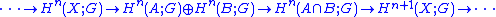
where the dimension preserving maps are restriction maps induced from inclusions, and the (co-)boundary maps are defined in a similar fashion to the homological version. There is also a relative formulation.
As an important special case when G is the group of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R and the underlying topological space has the additional structure of a smooth manifold, the Mayer–Vietoris sequence for de Rham cohomologyDe Rham cohomologyIn mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
is

where {U, V} is an open cover of X, ρ denotes the restriction map, and Δ is the difference. The map d* is defined similarly as the map ∂* from above. It can be briefly described as follows. For a cohomology class [ω] represented by closed formClosed and exact differential formsIn mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
ω in U∩V, express ω as a difference of forms ωU - ωV via a partition of unity subordinate to the open cover {U, V}, for example. The exterior derivative dωU and dωV agree on U∩V and therefore together define an n + 1 form σ on X. One then has d*([ω]) = [σ].
Derivation
Consider the long exact sequence associated to the short exact sequences of chain groups (constituent groups of chain complexChain complexIn mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es)
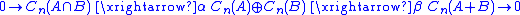
where α(x) = (x, −x), β(x, y) = x + y, and Cn(A + B) is the chain group consisting of sums of chains in A and chains in B. It is a fact that the singular n-simplices of X whose images are contained in either A or B generate all of the homology group Hn(X). In other words, Hn(A + B) is isomorphic to Hn(X). This gives the Mayer–Vietoris sequence for singular homology.
The same computation applied to the short exact sequences of vector spaces of differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s
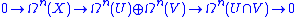
yields the Mayer–Vietoris sequence for de Rham cohomology.
From a formal point of view, the Mayer–Vietoris sequence can be derived from the Eilenberg–Steenrod axioms for homology theoriesHomology theoryIn mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
using the long exact sequence in homology.
Other homology theories
The derivation of the Mayer–Vietoris sequence from the Eilenberg–Steenrod axioms does not require the dimension axiom, so in addition to existing in ordinary cohomology theories, it holds in extraordinary cohomology theories (such as topological K-theoryTopological K-theoryIn mathematics, topological K-theory is a branch of algebraic topology. It was founded to study vector bundles on general topological spaces, by means of ideas now recognised as K-theory that were introduced by Alexander Grothendieck...
and cobordismCobordismIn mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
).
Sheaf cohomology
From the point of view of sheaf cohomologySheaf cohomologyIn mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
, the Mayer–Vietoris sequence is related to Čech cohomologyCech cohomologyIn mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
. Specifically, it arises from the degenerationSpectral sequenceIn homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
of the spectral sequenceSpectral sequenceIn homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
that relates Čech cohomology to sheaf cohomology (sometimes called the Mayer–Vietoris spectral sequence) in the case where the open cover used to compute the Čech cohomology consists of two open sets. This spectral sequence exists in arbitrary topoiToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
.



