Interior (topology)

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, specifically in topology

General topology

In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...

, the interior of a set S of points of a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 consists of all points of S that do not belong to the boundary

Boundary (topology)

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...

 of S. A point that is in the interior of S is an interior point of S.

Equivalently the interior of S is the complement of the closure

Closure (topology)

In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...

 of the complement of S. In this sense interior and closure are dual notions.

The exterior of a set is the interior of its complement, equivalently the complement of its closure; it consists of the points that are in neither the set nor its boundary. The interior, boundary, and exterior of a subset together partition

Partition of a set

In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...

 the whole space into three blocks (or fewer when one or more of these is empty). The interior and exterior are always open

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 while the boundary is always closed

Closed set

In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...

. Sets with empty interior (see examples below) are often called hollow.

Interior point

If S is a subset of a Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, then x is an interior point of S if there exists an open set

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

 centered at x which is contained in S.

This definition generalizes to any subset S of a metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

 X. Fully expressed, if X is a metric space with metric d, then x is an interior point of S if there exists r > 0, such that y is in S whenever the distance d(x, y) < r.

This definition generalises to topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

s by replacing "open ball" with "neighbourhood". Let S be a subset of a topological space X. Then x is an interior point of S if there exists a neighbourhood of x which is contained in S. Note that this definition does not depend upon whether neighbourhoods are required to be open. If neighbourhoods are not required to be open then S will automatically be a neighbourhood of x if S contains a neighbourhood of x.

Interior of a set

The interior of a set S is the set of all interior points of S. The interior of S is denoted int(S), Int(S), or S^o. The interior of a set has the following properties.

• int(S) is an open
  Open set
  The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
  
   subset of S.
• int(S) is the union of all open sets contained in S.
• int(S) is the largest open set contained in S.
• A set S is open if and only if
  If and only if
  In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
  
   S = int(S).
• int(int(S)) = int(S) (idempotence).
• If S is a subset of T, then int(S) is a subset of int(T).
• If A is an open set, then A is a subset of S if and only if A is a subset of int(S).

Sometimes the second or third property above is taken as the definition of the topological interior.

Note that these properties are also satisfied if "interior", "subset", "union", "contained in", "largest" and "open" are replaced by "closure", "superset", "intersection", "which contains", "smallest", and "closed", respectively. For more on this matter, see interior operator below.

Examples

• In any space, the interior of the empty set is the empty set.
• In any space X, if , int(A) is contained in A.
• If X is the Euclidean space of real number
  Real number
  In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
  
  s, then int([0, 1]) = (0, 1).
• If X is the Euclidean space , then the interior of the set 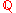of rational number
  Rational number
  In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
  
  s is empty.
• If X is the complex plane
  Complex number
  A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
  
   , then int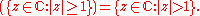
• In any Euclidean space, the interior of any finite set is the empty set.

On the set of real numbers one can put other topologies rather than the standard one.

• If , where has the lower limit topology
  Lower limit topology
  In mathematics, the lower limit topology or right half-open interval topology is a topology defined on the set R of real numbers; it is different from the standard topology on R and has a number of interesting properties...
  
  , then int([0, 1]) = [0, 1).
• If one considers on the topology in which every set is open, then int([0, 1]) = [0, 1].
• If one considers on the topology in which the only open sets are the empty set and itself, then int([0, 1]) is the empty set.

These examples show that the interior of a set depends upon the topology of the underlying space. The last two examples are special cases of the following.

• In any discrete space
  Discrete space
  In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
  
  , since every set is open, every set is equal to its interior.
• In any indiscrete space X, since the only open sets are the empty set and X itself, we have int(X) = X and for every proper subset
  Subset
  In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
  
   A of X, int(A) is the empty set.

Interior operator

The interior operator ^o is dual to the closure

Closure (topology)

In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...

 operator ^—, in the sense that

S^o = X \ (X \ S)^—,

and also

S^— = X \ (X \ S)^o

where X is the topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 containing S, and the backslash refers to the set-theoretic difference

Complement (set theory)

In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...

.

Therefore, the abstract theory of closure operators and the Kuratowski closure axioms

Kuratowski closure axioms

In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition...

 can be easily translated into the language of interior operators, by replacing sets with their complements.

Exterior of a set

The exterior of a subset S of a topological space X, denoted ext(S) or Ext(S), is the interior int(X \ S) of its relative complement. Alternatively, it can be defined as X \ S^—, the complement of the closure of S. Many properties follow in a straightforward way from those of the interior operator, such as the following.

• ext(S) is an open set that is disjoint with S.
• ext(S) is the union of all open sets that are disjoint with S.
• ext(S) is the largest open set that is disjoint with S.
• If S is a subset of T, then ext(S) is a superset of ext(T).

Unlike the interior operator, ext is not idempotent, but the following holds:

• ext(ext(S)) is a superset of int(S).

See also

• Algebraic interior
  Algebraic interior
  In functional analysis, a branch of mathematics, the algebraic interior or radial kernel of a subset of a vector space is a refinement of the concept of the interior. It is the subset of points contained in a given set that it is absorbing with respect to, i.e...
  
  
• Interior algebra
  Interior algebra
  In abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
  
  
• Jordan curve theorem
  Jordan curve theorem
  In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
  
  
• Quasi-relative interior
• Relative interior
  Relative interior
  In mathematics, the relative interior of a set is a refinement of the concept of the interior, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces...