Spectral sequence
Encyclopedia
In homological algebra
and algebraic topology
, a spectral sequence is a means of computing homology groups by taking successive approximations. Spectral sequences are a generalization of exact sequence
s, and since their introduction by , they have become an important research tool, particularly in homotopy theory.
, Jean Leray introduced the notion of a sheaf
and found himself faced with the problem of computing sheaf cohomology
. To compute sheaf cohomology, Leray introduced a computational technique now known as the Leray spectral sequence
. This gave a relation between cohomology groups of a sheaf and cohomology groups of the pushforward of the sheaf. The relation involved an infinite process. Leray found that the cohomology groups of the pushforward formed a natural chain complex
, so that he could take the cohomology of the cohomology. This was still not the cohomology of the original sheaf, but it was one step closer in a sense. The cohomology of the cohomology again formed a chain complex, and its cohomology formed a chain complex, and so on. The limit of this infinite process was essentially the same as the cohomology groups of the original sheaf.
It was soon realized that Leray's computational technique was an example of a more general phenomenon. Spectral sequences were found in diverse situations, and they gave intricate relationships among homology and cohomology groups coming from geometric situations such as fibration
s and from algebraic situations involving derived functors. While their theoretical importance has decreased since the introduction of derived categories
, they are still the most effective computational tool available. This is true even when many of the terms of the spectral sequence are incalculable.
Unfortunately, because of the large amount of information carried in spectral sequences, they are difficult to grasp. This information is usually contained in a rank three lattice of abelian group
s or modules
. The easiest cases to deal with are those in which the spectral sequence eventually collapses, meaning that going out further in the sequence produces no new information. Even when this does not happen, it is often possible to get useful information from a spectral sequence by various tricks.
, such as a category of modules over a ring. A spectral sequence is a choice of a nonnegative integer r0 and a collection of three sequences:
Usually the isomorphisms between Er+1 and H(Er) are suppressed, and we write equalities instead. Er+1 is sometimes called the derived object of Er.
The most elementary example is a chain complex
C•. C• is an object in an abelian category of chain complexes, and it comes with a differential d. Let r0 = 0, and let E0 be C•. This forces E1 to be the complex H(C•): At the i' th location this is the i' th homology group of C•. The only natural differential on this new complex is the zero map, so we let d1 = 0. This forces E2 to equal E1, and again our only natural differential is the zero map. Putting the zero differential on all the rest of our sheets gives a spectral sequence whose terms are:
The terms of this spectral sequence stabilize at the first sheet because its only nontrivial differential was on the zeroth sheet. Consequently we can get no more information at later steps. Usually, to get useful information from later sheets, we need extra structure on the Er.
In the ungraded situation described above, r0 is irrelevant, but in practice most spectral sequences occur in the category of doubly graded module
s over a ring
R (or doubly graded sheaves
of modules over a sheaf of rings). In this case, each sheet is a doubly graded module, so it decomposes as a direct sum of terms with one term for each possible bidegree. The boundary map is defined as the direct sum of boundary maps on each of the terms of the sheet. Their degree depends on r and is fixed by convention. For a homological spectral sequence, the terms are written
and the differentials have bidegree (-r,r-1). For a cohomological spectral sequence, the terms are written 
and the differentials have bidegree (r, 1 − r). (These choices of bidegree occur naturally in practice; see the example of a double complex below.) Depending upon the spectral sequence, the boundary map on the first sheet can have a degree which corresponds to r = 0, r = 1, or r = 2. For example, for the spectral sequence of a filtered complex, described below, r0 = 0, but for the Grothendieck spectral sequence
, r0 = 2. Usually r0 is zero, one, or two.
A morphism of spectral sequences E → E' is by definition a collection of maps fr : Er → E'r which are compatible with the differentials and with the given isomorphisms between cohomology of the r-th step and the (r + 1)-st sheets of E and E' , respectively. The category of spectral sequences is an abelian category.
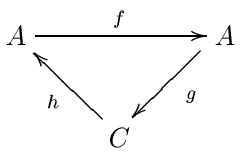
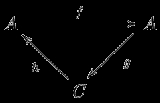
The most powerful technique for the construction of spectral sequences is William Massey's method of exact couples. Exact couples are particularly common in algebraic topology, where there are many spectral sequences for which no other construction is known. In fact, all known spectral sequences can be constructed using exact couples. Despite this they are unpopular in abstract algebra, where most spectral sequences come from filtered complexes. To define exact couples, we begin again with an abelian category. As before, in practice this is usually the category of doubly graded modules over a ring. An exact couple is a pair of objects A and C, together with three homomorphisms between these objects: f : A → A, g : A → C and h : C → A subject to certain exactness conditions:
We will abbreviate this data by (A, C, f, g, h). Exact couples are usually depicted as triangles. We will see that C corresponds to the E0 term of the spectral sequence and that A is some auxiliary data.
To pass to the next sheet of the spectral sequence, we will form the derived couple. We set:
From here it is straightforward to check that (A' , C' , f' , g' , h' ) is an exact couple. C' corresponds to the E1 term of the spectral sequence. We can iterate this procedure to get exact couples (A(n), C(n), f(n), g(n), h(n)). We let En be C(n) and dn be g(n) o h(n). This gives a spectral sequence.
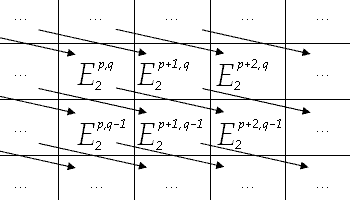A doubly graded spectral sequence has a tremendous amount of data to keep track of, but there is a common visualization technique which makes the structure of the spectral sequence clearer. We have three indices, r, p, and q. For each r, imagine that we have a sheet of graph paper. On this sheet, we will take p to be the horizontal direction and q to be the vertical direction. At each lattice point we have the object 
.
It is very common for n = p + q to be another natural index in the spectral sequence. n runs diagonally, northwest to southeast, across each sheet. In the homological case, the differentials have bidegree (−r, r − 1), so they decrease n by one. In the cohomological case, n is increased by one. When r is zero, the differential moves objects one space down or up. This is similar to the differential on a chain complex. When r is one, the differential moves objects one space to the left or right. When r is two, the differential moves objects just like a knight
's move in chess
. For higher r, the differential acts like a generalized knight's move.
cochain complex. This is a cochain complex C• together with a set of subcomplexes FpC•, where p ranges across all integers. (In practice, p is usually bounded on one side.) We require that the boundary map is compatible with the filtration; this means that d(FpCn) ⊆ FpCn+1. We assume that the filtration is descending, i.e., FpC• ⊇ Fp+1C•. We will number the terms of the cochain complex by n. Later, we will also assume that the filtration is Hausdorff or separated, that is, the intersection of the set of all FpC• is zero, and that the filtration is exhaustive, that is, the union of the set of all FpC• is the entire chain complex C•.
The filtration is useful because it gives a measure of nearness to zero: As p increases, FpC• gets closer and closer to zero. We will construct a spectral sequence from this filtration where coboundaries and cocycles in later sheets get closer and closer to coboundaries and cocycles in the original complex. This spectral sequence is doubly graded by the filtration degree p and the complementary degree q = n − p. (The complementary degree is often a more convenient index than the total degree n. For example, this is true of the spectral sequence of a double complex, explained below.)
We will construct this spectral sequence by hand. C• has only a single grading and a filtration, so we first construct a doubly graded object from C•. To get the second grading, we will take the associated graded object with respect to the filtration. We will write it in an unusual way which will be justified at the E1 step:
Since we assumed that the boundary map was compatible with the filtration, E0 is a doubly graded object and there is a natural doubly graded boundary map d0 on E0. To get E1, we take the homology of E0.
Notice that
and 
can be written as the images in 
of
and that we then have
is exactly the stuff which the differential pushes up one level in the filtration, and 
is exactly the image of the stuff which the differential pushes up zero levels in the filtration. This suggests that we should choose 
to be the stuff which the differential pushes up r levels in the filtration and 
to be image of the stuff which the differential pushes up r-1 levels in the filtration. In other words, the spectral sequence should satisfy
and we should have the relationship
For this to make sense, we must find a differential dr on each Er and verify that it leads to homology isomorphic to Er+1. The differential
is defined by restricting the original differential d defined on
to the subobject 
.
It is straightforward to check that the homology of Er with respect to this differential is Er+1, so this gives a spectral sequence. Unfortunately, the differential is not very explicit. Determining differentials or finding ways to work around them is one of the main challenges to successfully applying a spectral sequence.
and 
. We will do this by filtering our double complex in two different ways. Here are our filtrations:
To get a spectral sequence, we will reduce to the previous example. We define the total complex T(C•,•) to be the complex whose n' th term is 
and whose differential is d I + d II. This is a complex because d I and d II are anticommuting differentials. The two filtrations on Ci,j give two filtrations on the total complex:
To show that these spectral sequences give information about the iterated homologies, we will work out the E0, E1, and E2 terms of the I filtration on T(C•,•). The E0 term is clear:
To find the E1 term, we need to determine d I + d II on E0. Notice that the differential must have degree 1 with respect to n, so we get a map
Consequently, the differential on E0 is the map Cp,q → Cp,q−1 induced by d I + d II. But d I has the wrong degree to induce such a map, so d I must be zero on E0. That means the differential is exactly d II, so we get
To find E2, we need to determine
Because E1 was exactly the homology with respect to d II, d II is zero on E1. Consequently, we get
Using the other filtration gives us a different spectral sequence with a similar E2 term:
What remains is to find a relationship between these two spectral sequences. It will turn out that as r increases, the two sequences will become similar enough to allow useful comparisons.
In more general situations, limiting sheets often exist and are always interesting. They are one of the most powerful aspects of spectral sequences. We say that a spectral sequence
converges to or abuts to 
if there is an r(p, q) such that for all r ≥ r(p, q), the differentials 
and 
are zero. This forces 
to be isomorphic to 
for large r. In symbols, we write:
The p indicates the filtration index. It is very common to write the
term on the left-hand side of the abutment, because this is the most useful term of most spectral sequences.
In most spectral sequences, the
term is not naturally a doubly graded object. Instead, there are usually 
terms which come with a natural filtration 
. In these cases, we set 
. We define convergence in the same way as before, but we write
to mean that whenever p + q = n,
converges to 
.
The simplest situation in which we can determine convergence is when the spectral sequences degenerates. We say that the spectral sequences degenerates at sheet r if, for any s ≥ r, the differential ds is zero. This implies that Er ≅ Er+1 ≅ Er+2 ≅ ... In particular, it implies that Er is isomorphic to E∞. This is what happened in our first, trivial example of an unfiltered chain complex: The spectral sequence degenerated at the first sheet. In general, if a doubly graded spectral sequence is zero outside of a horizontal or vertical strip, the spectral sequence will degenerate, because later differentials will always go to or from an object not in the strip.
The spectral sequence also converges if
vanishes for all p less than some p0 and for all q less than some q0. If p0 and q0 can be chosen to be zero, this is called a first-quadrant spectral sequence. This sequence converges because each object is a fixed distance away from the edge of the non-zero region. Consequently, for a fixed p and q, the differential on later sheets always maps 
from or to the zero object; more visually, the differential leaves the quadrant where the terms are nonzero. The spectral sequence need not degenerate, however, because the differential maps might not all be zero at once. Similarly, the spectral sequence also converges if 
vanishes for all p greater than some p0 and for all q greater than some q0.
The five-term exact sequence
of a spectral sequence relates certain low-degree terms and E∞ terms.
We can ask what happens if we define
is a natural candidate for the abutment of this spectral sequence. Convergence is not automatic, but happens in many cases. In particular, if the filtration is finite and consists of exactly r nontrivial steps, then the spectral sequence degenerates after the r' th sheet. Convergence also occurs if the complex and the filtration are both bounded below or both bounded above.
To describe the abutment of our spectral sequence in more detail, notice that we have the formulas:
To see what this implies for
recall that we assumed that the filtration was separated. This implies that as r increases, the kernels shrink, until we are left with 
. For 
, recall that we assumed that the filtration was exhaustive. This implies that as r increases, the images grow until we reach 
. We conclude
,
that is, the abutment of the spectral sequence is the p' th graded part of the p+q' th homology of C. If our spectral sequence converges, then we conclude that:
This gives:
The differential has bidegree (1, 0), so d0,q : Hq(C•) → Hq+1(A•). These are the connecting homomorphisms from the snake lemma
, and together with the maps A• → B• → C•, they give a sequence:
It remains to show that this sequence is exact at the A and C spots. Notice that this spectral sequence degenerates at the E2 term because the differentials have bidegree (2, −1). Consequently, the E2 term is the same as the E∞ term:
But we also have a direct description of the E2 term as the homology of the E1 term. These two descriptions must be isomorphic:
The former gives exactness at the C spot, and the latter gives exactness at the A spot.
In general, the two gradings on Hp+q(T(C•,•)) are distinct. Despite this, it is still possible to gain useful information from these two spectral sequences.
. Tor is defined using a projective resolution of its first argument. However, it turns out that Tori(M, N) = Tori(N, M). While this can be verified without a spectral sequence, it is very easy with spectral sequences.
Choose projective resolutions P• and Q• of M and N, respectively. Consider these as complexes which vanish in negative degree having differentials d and e, respectively. We can construct a double complex whose terms are Ci,j = Pi ⊗ Qj and whose differentials are d ⊗ 1 and (−1)i(1 ⊗ e). (The factor of −1 is so that the differentials anticommute.) Since projective modules are flat, taking the tensor product with a projective module commutes with taking homology, so we get:
Since the two complexes are resolutions, their homology vanishes outside of degree zero. In degree zero, we are left with
In particular, the
terms vanish except along the lines q = 0 (for the I spectral sequence) and p = 0 (for the II spectral sequence). This implies that the spectral sequence degenerates at the second sheet, so the E∞ terms are isomorphic to the E2 terms:
Finally, when p and q are equal, the two right-hand sides are equal, and the commutativity of Tor follows.
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
and algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a spectral sequence is a means of computing homology groups by taking successive approximations. Spectral sequences are a generalization of exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
s, and since their introduction by , they have become an important research tool, particularly in homotopy theory.
Discovery and motivation
Motivated by problems in algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, Jean Leray introduced the notion of a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
and found himself faced with the problem of computing sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
. To compute sheaf cohomology, Leray introduced a computational technique now known as the Leray spectral sequence
Leray spectral sequence
In mathematics, the Leray spectral sequence was a pioneering example in homological algebra, introduced in 1946 by Jean Leray. The formulation was of a spectral sequence, expressing the relationship holding in sheaf cohomology between two topological spaces X and Y, and set up by a continuous...
. This gave a relation between cohomology groups of a sheaf and cohomology groups of the pushforward of the sheaf. The relation involved an infinite process. Leray found that the cohomology groups of the pushforward formed a natural chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
, so that he could take the cohomology of the cohomology. This was still not the cohomology of the original sheaf, but it was one step closer in a sense. The cohomology of the cohomology again formed a chain complex, and its cohomology formed a chain complex, and so on. The limit of this infinite process was essentially the same as the cohomology groups of the original sheaf.
It was soon realized that Leray's computational technique was an example of a more general phenomenon. Spectral sequences were found in diverse situations, and they gave intricate relationships among homology and cohomology groups coming from geometric situations such as fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s and from algebraic situations involving derived functors. While their theoretical importance has decreased since the introduction of derived categories
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
, they are still the most effective computational tool available. This is true even when many of the terms of the spectral sequence are incalculable.
Unfortunately, because of the large amount of information carried in spectral sequences, they are difficult to grasp. This information is usually contained in a rank three lattice of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s or modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. The easiest cases to deal with are those in which the spectral sequence eventually collapses, meaning that going out further in the sequence produces no new information. Even when this does not happen, it is often possible to get useful information from a spectral sequence by various tricks.
Formal definition
Fix an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, such as a category of modules over a ring. A spectral sequence is a choice of a nonnegative integer r0 and a collection of three sequences:
- For all integers r ≥ r0, an object Er, called a sheet (as in a sheet of paperPaperPaper is a thin material mainly used for writing upon, printing upon, drawing or for packaging. It is produced by pressing together moist fibers, typically cellulose pulp derived from wood, rags or grasses, and drying them into flexible sheets....
), or sometimes a page or a term, - Endomorphisms dr : Er → Er satisfying dr o dr = 0, called boundary maps or differentials,
- Isomorphisms of Er+1 with H(Er), the homology of Er with respect to dr.
Usually the isomorphisms between Er+1 and H(Er) are suppressed, and we write equalities instead. Er+1 is sometimes called the derived object of Er.
The most elementary example is a chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
C•. C• is an object in an abelian category of chain complexes, and it comes with a differential d. Let r0 = 0, and let E0 be C•. This forces E1 to be the complex H(C•): At the i
- E0 = C•
- Er = H(C•) for all r ≥ 1.
The terms of this spectral sequence stabilize at the first sheet because its only nontrivial differential was on the zeroth sheet. Consequently we can get no more information at later steps. Usually, to get useful information from later sheets, we need extra structure on the Er.
In the ungraded situation described above, r0 is irrelevant, but in practice most spectral sequences occur in the category of doubly graded module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R (or doubly graded sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of modules over a sheaf of rings). In this case, each sheet is a doubly graded module, so it decomposes as a direct sum of terms with one term for each possible bidegree. The boundary map is defined as the direct sum of boundary maps on each of the terms of the sheet. Their degree depends on r and is fixed by convention. For a homological spectral sequence, the terms are written
and the differentials have bidegree (-r,r-1). For a cohomological spectral sequence, the terms are written and the differentials have bidegree (r, 1 − r). (These choices of bidegree occur naturally in practice; see the example of a double complex below.) Depending upon the spectral sequence, the boundary map on the first sheet can have a degree which corresponds to r = 0, r = 1, or r = 2. For example, for the spectral sequence of a filtered complex, described below, r0 = 0, but for the Grothendieck spectral sequenceGrothendieck spectral sequence
In mathematics, in the field of homological algebra, the Grothendieck spectral sequence is a technique that allows one to compute the derived functors of the composition of two functors G\circ F, from knowledge of the derived functors of F and G.If...
, r0 = 2. Usually r0 is zero, one, or two.
A morphism of spectral sequences E → E' is by definition a collection of maps fr : Er → E'r which are compatible with the differentials and with the given isomorphisms between cohomology of the r-th step and the (r + 1)-st sheets of E and E' , respectively. The category of spectral sequences is an abelian category.
Exact couples
The most powerful technique for the construction of spectral sequences is William Massey's method of exact couples. Exact couples are particularly common in algebraic topology, where there are many spectral sequences for which no other construction is known. In fact, all known spectral sequences can be constructed using exact couples. Despite this they are unpopular in abstract algebra, where most spectral sequences come from filtered complexes. To define exact couples, we begin again with an abelian category. As before, in practice this is usually the category of doubly graded modules over a ring. An exact couple is a pair of objects A and C, together with three homomorphisms between these objects: f : A → A, g : A → C and h : C → A subject to certain exactness conditions:
- ImageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
f = KernelKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
g - Image g = Kernel h
- Image h = Kernel f
We will abbreviate this data by (A, C, f, g, h). Exact couples are usually depicted as triangles. We will see that C corresponds to the E0 term of the spectral sequence and that A is some auxiliary data.
To pass to the next sheet of the spectral sequence, we will form the derived couple. We set:
- d = g o h
- A
' = f(A) - C
' = Ker d / Im d - f
' = f|A' , the restriction of f to A' - h
' : C' → A' is induced by h. It is straightforward to see that h induces such a map. - g
' : A' → C' is defined on elements as follows: For each a in A' , write a as f(b) for some b in A. g' (a) is defined to be the image of g(b) in C' . In general, g' can be constructed using one of the embedding theorems for abelian categories.
From here it is straightforward to check that (A
Visualization
.It is very common for n = p + q to be another natural index in the spectral sequence. n runs diagonally, northwest to southeast, across each sheet. In the homological case, the differentials have bidegree (−r, r − 1), so they decrease n by one. In the cohomological case, n is increased by one. When r is zero, the differential moves objects one space down or up. This is similar to the differential on a chain complex. When r is one, the differential moves objects one space to the left or right. When r is two, the differential moves objects just like a knight
Knight (chess)
The knight is a piece in the game of chess, representing a knight . It is normally represented by a horse's head and neck. Each player starts with two knights, which begin on the row closest to the player, one square from the corner...
's move in chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
. For higher r, the differential acts like a generalized knight's move.
The spectral sequence of a filtered complex
A very common type of spectral sequence comes from a filteredFiltration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
cochain complex. This is a cochain complex C• together with a set of subcomplexes FpC•, where p ranges across all integers. (In practice, p is usually bounded on one side.) We require that the boundary map is compatible with the filtration; this means that d(FpCn) ⊆ FpCn+1. We assume that the filtration is descending, i.e., FpC• ⊇ Fp+1C•. We will number the terms of the cochain complex by n. Later, we will also assume that the filtration is Hausdorff or separated, that is, the intersection of the set of all FpC• is zero, and that the filtration is exhaustive, that is, the union of the set of all FpC• is the entire chain complex C•.
The filtration is useful because it gives a measure of nearness to zero: As p increases, FpC• gets closer and closer to zero. We will construct a spectral sequence from this filtration where coboundaries and cocycles in later sheets get closer and closer to coboundaries and cocycles in the original complex. This spectral sequence is doubly graded by the filtration degree p and the complementary degree q = n − p. (The complementary degree is often a more convenient index than the total degree n. For example, this is true of the spectral sequence of a double complex, explained below.)
We will construct this spectral sequence by hand. C• has only a single grading and a filtration, so we first construct a doubly graded object from C•. To get the second grading, we will take the associated graded object with respect to the filtration. We will write it in an unusual way which will be justified at the E1 step:
Since we assumed that the boundary map was compatible with the filtration, E0 is a doubly graded object and there is a natural doubly graded boundary map d0 on E0. To get E1, we take the homology of E0.
Notice that
and can be written as the images in ofand that we then have
is exactly the stuff which the differential pushes up one level in the filtration, and is exactly the image of the stuff which the differential pushes up zero levels in the filtration. This suggests that we should choose to be the stuff which the differential pushes up r levels in the filtration and to be image of the stuff which the differential pushes up r-1 levels in the filtration. In other words, the spectral sequence should satisfyand we should have the relationship
For this to make sense, we must find a differential dr on each Er and verify that it leads to homology isomorphic to Er+1. The differential
is defined by restricting the original differential d defined on
to the subobject .It is straightforward to check that the homology of Er with respect to this differential is Er+1, so this gives a spectral sequence. Unfortunately, the differential is not very explicit. Determining differentials or finding ways to work around them is one of the main challenges to successfully applying a spectral sequence.
The spectral sequence of a double complex
Another common spectral sequence is the spectral sequence of a double complex. A double complex is a collection of objects Ci,j for all integers i and j together with two differentials, d I and d II. d I is assumed to decrease i, and d II is assumed to decrease j. Furthermore, we assume that the differentials anticommute, so that d I d II + d II d I = 0. Our goal is to compare the iterated homologies and . We will do this by filtering our double complex in two different ways. Here are our filtrations:To get a spectral sequence, we will reduce to the previous example. We define the total complex T(C•,•) to be the complex whose n
and whose differential is d I + d II. This is a complex because d I and d II are anticommuting differentials. The two filtrations on Ci,j give two filtrations on the total complex:To show that these spectral sequences give information about the iterated homologies, we will work out the E0, E1, and E2 terms of the I filtration on T(C•,•). The E0 term is clear:
To find the E1 term, we need to determine d I + d II on E0. Notice that the differential must have degree 1 with respect to n, so we get a map
Consequently, the differential on E0 is the map Cp,q → Cp,q−1 induced by d I + d II. But d I has the wrong degree to induce such a map, so d I must be zero on E0. That means the differential is exactly d II, so we get
To find E2, we need to determine
Because E1 was exactly the homology with respect to d II, d II is zero on E1. Consequently, we get
Using the other filtration gives us a different spectral sequence with a similar E2 term:
What remains is to find a relationship between these two spectral sequences. It will turn out that as r increases, the two sequences will become similar enough to allow useful comparisons.
Convergence, degeneration, and abutment
In the elementary example that we began with, the sheets of the spectral sequence were constant once r was at least 1. In that setup it makes sense to take the limit of the sequence of sheets: Since nothing happens after the zeroth sheet, the limiting sheet E∞ is the same as E1.In more general situations, limiting sheets often exist and are always interesting. They are one of the most powerful aspects of spectral sequences. We say that a spectral sequence
converges to or abuts to if there is an r(p, q) such that for all r ≥ r(p, q), the differentials and are zero. This forces to be isomorphic to for large r. In symbols, we write:The p indicates the filtration index. It is very common to write the
term on the left-hand side of the abutment, because this is the most useful term of most spectral sequences.In most spectral sequences, the
term is not naturally a doubly graded object. Instead, there are usually terms which come with a natural filtration . In these cases, we set . We define convergence in the same way as before, but we writeto mean that whenever p + q = n,
converges to .The simplest situation in which we can determine convergence is when the spectral sequences degenerates. We say that the spectral sequences degenerates at sheet r if, for any s ≥ r, the differential ds is zero. This implies that Er ≅ Er+1 ≅ Er+2 ≅ ... In particular, it implies that Er is isomorphic to E∞. This is what happened in our first, trivial example of an unfiltered chain complex: The spectral sequence degenerated at the first sheet. In general, if a doubly graded spectral sequence is zero outside of a horizontal or vertical strip, the spectral sequence will degenerate, because later differentials will always go to or from an object not in the strip.
The spectral sequence also converges if
vanishes for all p less than some p0 and for all q less than some q0. If p0 and q0 can be chosen to be zero, this is called a first-quadrant spectral sequence. This sequence converges because each object is a fixed distance away from the edge of the non-zero region. Consequently, for a fixed p and q, the differential on later sheets always maps from or to the zero object; more visually, the differential leaves the quadrant where the terms are nonzero. The spectral sequence need not degenerate, however, because the differential maps might not all be zero at once. Similarly, the spectral sequence also converges if vanishes for all p greater than some p0 and for all q greater than some q0.The five-term exact sequence
Five-term exact sequence
In mathematics, five-term exact sequence or exact sequence of low-degree terms is a sequence of terms related to the first step of a spectral sequence.More precisely, letbe a spectral sequence, whose terms are non-trivial only for p, q ≥ 0....
of a spectral sequence relates certain low-degree terms and E∞ terms.
The spectral sequence of a filtered complex, continued
Notice that we have a chain of inclusions:We can ask what happens if we define
is a natural candidate for the abutment of this spectral sequence. Convergence is not automatic, but happens in many cases. In particular, if the filtration is finite and consists of exactly r nontrivial steps, then the spectral sequence degenerates after the rTo describe the abutment of our spectral sequence in more detail, notice that we have the formulas:
To see what this implies for
recall that we assumed that the filtration was separated. This implies that as r increases, the kernels shrink, until we are left with . For , recall that we assumed that the filtration was exhaustive. This implies that as r increases, the images grow until we reach . We conclude,that is, the abutment of the spectral sequence is the p
Long exact sequences
Using the spectral sequence of a filtered complex, we can derive the existence of long exact sequences. Choose a short exact sequence of cochain complexes 0 → A• → B• → C• → 0, and call the first map f• : A• → B•. We get natural maps of homology objects Hn(A•) → Hn(B•) → Hn(C•), and we know that this is exact in the middle. We will use the spectral sequence of a filtered complex to find the connecting homomorphism and to prove that the resulting sequence is exact. To start, we filter B•:This gives:
The differential has bidegree (1, 0), so d0,q : Hq(C•) → Hq+1(A•). These are the connecting homomorphisms from the snake lemma
Snake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
, and together with the maps A• → B• → C•, they give a sequence:
It remains to show that this sequence is exact at the A and C spots. Notice that this spectral sequence degenerates at the E2 term because the differentials have bidegree (2, −1). Consequently, the E2 term is the same as the E∞ term:
But we also have a direct description of the E2 term as the homology of the E1 term. These two descriptions must be isomorphic:
The former gives exactness at the C spot, and the latter gives exactness at the A spot.
The spectral sequence of a double complex, continued
Using the abutment for a filtered complex, we find that:In general, the two gradings on Hp+q(T(C•,•)) are distinct. Despite this, it is still possible to gain useful information from these two spectral sequences.
Commutativity of Tor
Let R be a ring, let M be a right R-module and N a left R-module. Recall that the derived functors of the tensor product are denoted TorTor functor
In homological algebra, the Tor functors are the derived functors of the tensor product functor. They were first defined in generality to express the Künneth theorem and universal coefficient theorem in algebraic topology....
. Tor is defined using a projective resolution of its first argument. However, it turns out that Tori(M, N) = Tori(N, M). While this can be verified without a spectral sequence, it is very easy with spectral sequences.
Choose projective resolutions P• and Q• of M and N, respectively. Consider these as complexes which vanish in negative degree having differentials d and e, respectively. We can construct a double complex whose terms are Ci,j = Pi ⊗ Qj and whose differentials are d ⊗ 1 and (−1)i(1 ⊗ e). (The factor of −1 is so that the differentials anticommute.) Since projective modules are flat, taking the tensor product with a projective module commutes with taking homology, so we get:
Since the two complexes are resolutions, their homology vanishes outside of degree zero. In degree zero, we are left with
In particular, the
terms vanish except along the lines q = 0 (for the I spectral sequence) and p = 0 (for the II spectral sequence). This implies that the spectral sequence degenerates at the second sheet, so the E∞ terms are isomorphic to the E2 terms:Finally, when p and q are equal, the two right-hand sides are equal, and the commutativity of Tor follows.
Further examples
Some notable spectral sequences are:- Adams spectral sequenceAdams spectral sequenceIn mathematics, the Adams spectral sequence is a spectral sequence introduced by . Like all spectral sequences, it is a computational tool; it relates homology theory to what is now called stable homotopy theory...
in stable homotopy theoryStable homotopy theoryIn mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor... - Adams–Novikov spectral sequence, a generalization to extraordinary cohomology theories.
- Atiyah–Hirzebruch spectral sequence of an extraordinary cohomology theory
- Bar spectral sequence for the homology of the classifying space of a group.
- Barratt spectral sequence converging to the homotopy of the initial space of a cofibration.
- Bloch–Lichtenbaum spectral sequence converging to the algebraic K-theory of a field.
- Bockstein spectral sequenceBockstein spectral sequenceIn mathematics, the Bockstein spectral sequence is a spectral sequence relating the homology with mod p coefficients and the homology reduced mod p. It is named after Meyer Bockstein....
relating the homology with mod p coefficients and the homology reduced mod p. - Bousfield–Kan spectral sequence converging to the homotopy colimit of a functor.
- Cartan–Leray spectral sequence converging to the homology of a quotient space.
- Čech-to-derived functor spectral sequenceCech-to-derived functor spectral sequenceIn algebraic topology, a branch of mathematics, the Čech-to-derived functor spectral sequence is a spectral sequence that relates Čech cohomology of a sheaf and sheaf cohomology....
from Čech cohomologyCech cohomologyIn mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
to sheaf cohomologySheaf cohomologyIn mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
. - Change of rings spectral sequences for calculating Tor and Ext groups of modules.
- Chromatic spectral sequenceChromatic spectral sequenceIn mathematics, the chromatic spectral sequence is a spectral sequence, introduced by , used for calculating the initial term of the Adams–Novikov spectral sequence for BP cohomology, which is in turn used for calculating the stable homotopy groups of spheres....
for calculating the initial terms of the Adams–Novikov spectral sequence. - Connes spectral sequences converging to the cyclic homology of an algebra.
- EHP spectral sequenceEHP spectral sequenceIn mathematics, the EHP spectral sequence is a spectral sequence used for inductively calculating the homotopy groups of sphereslocalized at some prime p. It is described in more detail in and...
converging to stable homotopy groups of spheres - Eilenberg–Moore spectral sequence for the singular cohomology of the pullbackPullbackSuppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
of a fibrationFibrationIn topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same... - Federer spectral sequence converging to homotopy groups of a function space.
- Fröhlicher spectral sequenceFröhlicher spectral sequenceIn mathematics, the Fröhlicher spectral sequence is a tool in the theory of complex manifolds, for expressing the potential failure of the results of cohomology theory that are valid in general only for Kähler manifolds. A spectral sequence is set up, the degeneration of which would give the...
starting from the Dolbeault cohomologyDolbeault cohomologyIn mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold...
and converging to the algebraic de Rham cohomology of a variety. - Green's spectral sequence for Koszul cohomology
- Grothendieck spectral sequenceGrothendieck spectral sequenceIn mathematics, in the field of homological algebra, the Grothendieck spectral sequence is a technique that allows one to compute the derived functors of the composition of two functors G\circ F, from knowledge of the derived functors of F and G.If...
for composing derived functorDerived functorIn mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s - Hodge–de Rham spectral sequence converging to the algebraic de Rham cohomology of a variety.
- Hurewicz spectral sequence for calculating the homology of a space from its homotopy.
- Hyperhomology spectral sequence for calculating hyper homology.
- Kunneth spectral sequence for calculating the homology of a tensor product of differential algebras.
- Leray spectral sequenceLeray spectral sequenceIn mathematics, the Leray spectral sequence was a pioneering example in homological algebra, introduced in 1946 by Jean Leray. The formulation was of a spectral sequence, expressing the relationship holding in sheaf cohomology between two topological spaces X and Y, and set up by a continuous...
converging to the cohomology of a sheaf. - Leray–Serre spectral sequence of a fibrationFibrationIn topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
- Lyndon–Hochschild–Serre spectral sequence in group (co)homologyGroup cohomologyIn abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
- May spectral sequenceMay spectral sequenceIn mathematics, the May spectral sequence is a spectral sequence, introduced by , used for calculating the initial term of the Adams spectral sequence, which is in turn used for calculating the stable homotopy groups of spheres. It is described in detail in ....
for calculating the Tor or Ext groups of an algebra. - Miller spectral sequence converging to the mod p stable homology of a space.
- Milnor spectral sequence is another name for the bar spectral sequence.
- Moore spectral sequence is another name for the bar spectral sequence.
- Quillen spectral sequence for calculating the homotopy of a simplicial group.
- Rothenberg–Steenrod spectral sequence is another name for the bar spectral sequence.
- Spectral sequence of a differential filtered group: described in this article.
- Spectral sequence of a double complex: described in this article.
- Spectral sequence of an exact couple: described in this article.
- Universal coefficient spectral sequence
- van Est spectral sequence converging to relative Lie algebra cohomology.
- van Kampen spectral sequence for calculating the homotopy of a wedge of spaces.