Cech cohomology
Encyclopedia
In mathematics
, specifically algebraic topology
, Čech cohomology is a cohomology
theory based on the intersection properties of open
covers
of a topological space
. It is named for the mathematician Eduard Čech
.
be an open cover of X. Define a simplicial complex
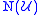, called the nerve of the covering, as follows:
Geometrically, the nerve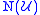
is essentially a "dual complex" (in the sense of a dual graph
, or Poincaré duality
) for the covering
.
The idea of Čech cohomology is that, if we choose a cover
consisting of sufficiently small, connected open sets, the resulting simplicial complex 
should be a good combinatorial model for the space X. For such a cover, the Čech cohomology of X is defined to be the simplicial
cohomology
of the nerve.
This idea can be formalized by the notion of a good cover, for which every open set and every finite intersection of open sets is contractible. However, a more general approach is to take the direct limit
of the cohomology groups of the nerve over the system of all possible open covers of X, ordered by refinement. This is the approach adopted below.
be a topological space
, and let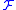
be a presheaf of abelian group
s on
. Let 
be an open cover of 
.
of 
is an ordered collection of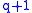 
sets chosen from 
, such that the intersection of all these sets is non-empty. This intersection is called the support of 
and is denoted 
.
Now let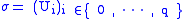
be such a q-simplex. The j-th partial boundary of 
is defined to be the q-1-simplex obtained by removing the j-th set from 
, that is:
The boundary of
is defined as the alternating sum of the partial boundaries: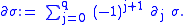
with coefficients in 
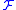is a map which associates to each q-simplex σ an element of 
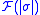and we denote the set of all q-cochains of 
with coefficients in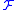 
by 
. 
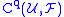is an abelian group by pointwise addition.
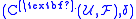by defining a coboundary operator (also called codifferential)
,
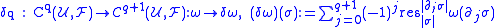(where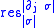
is the restriction morphism
from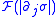
to 
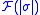), and showing that 
.
is the set of all q-cocycles.
Thus a (q-1)-cochain f is a cocycle if for all q-simplices σ the cocycle condition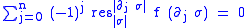
holds. In particular, a 1-cochain f is a 1-cocycle if
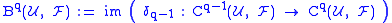is the set of all q-coboundaries.
For example, a 1-cochain f is a 1-coboundary if there exists a 0-cochain h such that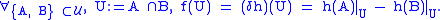
with values in 
is defined to be the cohomology of the cochain complex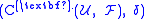 
. Thus the qth Čech cohomology is given by
.
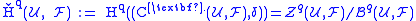The Čech cohomology of X is defined by considering refinements of open covers. If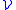
is a refinement of 
then there is a map in cohomology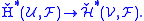 
The open covers of X form a directed set
under refinement, so the above map leads to a direct system of abelian groups. The Čech cohomology of X with values in F is defined as the direct limit
of this system.
The Čech cohomology of X with coefficients in a fixed abelian group A, denoted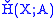
, is defined as 
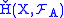where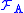 
is the constant sheaf
on X determined by A.
A variant of Čech cohomology, called numerable Čech cohomology, is defined as above, except that all open covers considered are required to be numerable: that is, there is a partition of unity {ρi} such that each support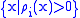
is contained in some element of the cover. If X is paracompact and Hausdorff
, then numerable Čech cohomology agrees with the usual Čech cohomology.
is homotopy equivalent to a CW complex
, then the Čech cohomology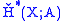
is naturally isomorphic to the singular cohomology
. If X is a differentiable manifold
, then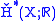
is also naturally isomorphic to the de Rham cohomology
; the article on de Rham cohomology provides a brief review of this isomorphism. For less well-behaved spaces, Čech cohomology differs from singular cohomology. For example if X is the closed topologist's sine curve
, then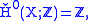
whereas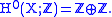 
If X is a differentiable manifold and the cover
of X is a "good cover" (i.e. all the sets Uα are contractible
to a point, and all finite intersections of sets in
are either empty or contractible to a point), then
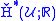is isomorphic to the de Rham cohomology.
If X is compact Hausdorff, then Čech cohomology (with coefficients in a discrete group) is isomorphic to Alexander-Spanier cohomology
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, Čech cohomology is a cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
theory based on the intersection properties of open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
covers
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. It is named for the mathematician Eduard Čech
Eduard Cech
Eduard Čech was a Czech mathematician born in Stračov, Bohemia . His research interests included projective differential geometry and topology. In 1921–1922 he collaborated with Guido Fubini in Turin...
.
Motivation
Let X be a topological space, and let be an open cover of X. Define a simplicial complexSimplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
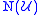, called the nerve of the covering, as follows:
- There is one vertex for each element of
. - There is one edge for each pair
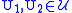such that 
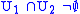. - In general, there is one k-simplex for each k+1-element subset
of 
for which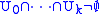 
.
Geometrically, the nerve
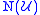is essentially a "dual complex" (in the sense of a dual graphDual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
, or Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
) for the covering
.The idea of Čech cohomology is that, if we choose a cover
consisting of sufficiently small, connected open sets, the resulting simplicial complex should be a good combinatorial model for the space X. For such a cover, the Čech cohomology of X is defined to be the simplicialSimplicial homology
In mathematics, in the area of algebraic topology, simplicial homology is a theory with a finitary definition, and is probably the most tangible variant of homology theory....
cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of the nerve.
This idea can be formalized by the notion of a good cover, for which every open set and every finite intersection of open sets is contractible. However, a more general approach is to take the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of the cohomology groups of the nerve over the system of all possible open covers of X, ordered by refinement. This is the approach adopted below.
Construction
Let be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, and let
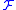be a presheaf of abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s on
. Let be an open cover of .Simplex
A q-simplex of is an ordered collection of sets chosen from , such that the intersection of all these sets is non-empty. This intersection is called the support of and is denoted .Now let
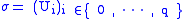be such a q-simplex. The j-th partial boundary of is defined to be the q-1-simplex obtained by removing the j-th set from , that is:The boundary of
is defined as the alternating sum of the partial boundaries: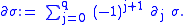Cochain
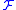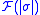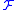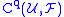A q-cochain of with coefficients in is a map which associates to each q-simplex σ an element of and we denote the set of all q-cochains of with coefficients in by . is an abelian group by pointwise addition.Differential
The cochain groups can be made into a cochain complex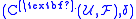 by defining a coboundary operator (also called codifferential)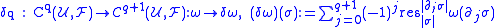,(where
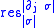is the restriction morphismSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
from
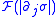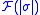to ), and showing that .Cocycle
A q-cochain is called a q-cocycle if it is in the kernel of δ and is the set of all q-cocycles.Thus a (q-1)-cochain f is a cocycle if for all q-simplices σ the cocycle condition
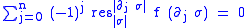holds. In particular, a 1-cochain f is a 1-cocycle ifCoboundary
A q-cochain is called a q-coboundary if it is in the image of δ and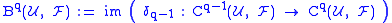 is the set of all q-coboundaries.For example, a 1-cochain f is a 1-coboundary if there exists a 0-cochain h such that
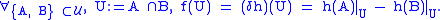
Cohomology
The Čech cohomology of with values in is defined to be the cohomology of the cochain complex 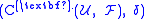. Thus the qth Čech cohomology is given by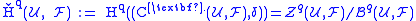.The Čech cohomology of X is defined by considering refinements of open covers. If
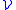is a refinement of then there is a map in cohomology 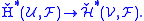The open covers of X form a directed set
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
under refinement, so the above map leads to a direct system of abelian groups. The Čech cohomology of X with values in F is defined as the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of this system.The Čech cohomology of X with coefficients in a fixed abelian group A, denoted
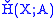, is defined as 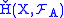where 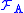is the constant sheafConstant sheaf
In mathematics, the constant sheaf on a topological space X associated to a set A is a sheaf of sets on X whose stalks are all equal to A. It is denoted by or AX. The constant presheaf with value A is the presheaf that assigns to each open subset of X the value A, and all of whose restriction maps...
on X determined by A.
A variant of Čech cohomology, called numerable Čech cohomology, is defined as above, except that all open covers considered are required to be numerable: that is, there is a partition of unity {ρi} such that each support
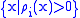is contained in some element of the cover. If X is paracompact and HausdorffHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, then numerable Čech cohomology agrees with the usual Čech cohomology.
Relation to other cohomology theories
If is homotopy equivalent to a CW complexCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
, then the Čech cohomology
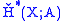is naturally isomorphic to the singular cohomologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
. If X is a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, then
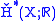is also naturally isomorphic to the de Rham cohomologyDe Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
; the article on de Rham cohomology provides a brief review of this isomorphism. For less well-behaved spaces, Čech cohomology differs from singular cohomology. For example if X is the closed topologist's sine curve
Topologist's sine curve
In the branch of mathematics known as topology, the topologist's sine curve is a topological space with several interesting properties that make it an important textbook example....
, then
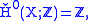whereas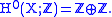 If X is a differentiable manifold and the cover
of X is a "good cover" (i.e. all the sets Uα are contractibleContractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
to a point, and all finite intersections of sets in
are either empty or contractible to a point), then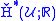 is isomorphic to the de Rham cohomology.If X is compact Hausdorff, then Čech cohomology (with coefficients in a discrete group) is isomorphic to Alexander-Spanier cohomology
Alexander-Spanier cohomology
In mathematics, particularly in algebraic topology, Alexander–Spanier cohomology is a cohomologytheory for topological spaces, introduced by for the special case of compact metric spaces, and by for all topological spaces, based on a suggestion of A. D...
.