
Homotopy groups of spheres
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
terms, the structure of spheres viewed as topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, forgetting about their precise geometry. Unlike homology groups, which are also topological invariants, the homotopy groups are surprisingly complex and difficult to compute.
The n-dimensional unit sphere — called the n-sphere for brevity, and denoted as Sn — generalizes the familiar circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
(S1) and the ordinary sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
(S2). The n-sphere may be defined geometrically as the set of points in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of dimension n + 1 located at a unit distance from the origin. The i-th homotopy group πi(Sn) summarizes the different ways in which the i-dimensional sphere Si can be mapped
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
continuously into the n-dimensional sphere Sn. This summary does not distinguish between two mappings if one can be continuously deformed
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
to the other; thus, only equivalence classes of mappings are summarized. An "addition" operation defined on these equivalence classes makes the set of equivalence classes into an abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
The problem of determining πi(Sn) falls into three regimes, depending on whether i is less than, equal to, or greater than n. For 0 < i < n, any mapping from Si to Sn is homotopic (i.e., continuously deformable) to a constant mapping, i.e., a mapping that maps all of Si to a single point of Sn. When i = n, every map from Sn to itself has a degree that measures how many times the sphere is wrapped around itself. This degree identifies πn(Sn) with the group of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s under addition. For example, every point on a circle can be mapped continuously onto a point of another circle; as the first point is moved around the first circle, the second point may cycle several times around the second circle, depending on the particular mapping. However, the most interesting and surprising results occur when i > n. The first such surprise was the discovery of a mapping called the Hopf fibration, which wraps the 3-sphere S3 around the usual sphere S2 in a non-trivial fashion, and so is not equivalent to a one-point mapping.
The question of computing the homotopy group πn+k(Sn) for positive k turned out to be a central question in algebraic topology that has contributed to development of many of its fundamental techniques and has served as a stimulating focus of research. One of the main discoveries is that the homotopy groups πn+k(Sn) are independent of n for n ≥ k + 2. These are called the stable homotopy groups of spheres and have been computed for values of k up to 64. The stable homotopy groups form the coefficient ring of an extraordinary cohomology theory, called stable cohomotopy theory. The unstable homotopy groups (for n < k + 2) are more erratic; nevertheless, they have been tabulated for k < 20. Most modern computations use spectral sequence
Spectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
s, a technique first applied to homotopy groups of spheres by Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
. Several important patterns have been established, yet much remains unknown and unexplained.
Background
The study of homotopy groups of spheres builds on a great deal of background material, here briefly reviewed. Algebraic topologyAlgebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
provides the larger context, itself built on topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, with homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s as a basic example.
n-sphere
An ordinary sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
in three-dimensional space — the surface, not the solid ball — is just one example of what a sphere means in topology. Geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
defines a sphere rigidly, as a shape. Here are some alternatives.
- Implicit surface: x02 + x12 + x22 = 1
- This is the set of points in 3-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
found exactly one unit away from the origin. It is called the 2-sphere, S2, for reasons given below. The same idea applies for any dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
n; the equation x02 + x12 + ⋯ + xn2 = 1 produces the n-sphere as a geometric object in (n + 1)-dimensional space. For example, the 1-sphere S1 is a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.- Disk with collapsed rim: written in topology as D2/S1
- This construction moves from geometry to pure topology. The disk D2 is the region contained by a circle, described by the inequality x02 + x12 ≤ 1, and its rim (or "boundaryBoundary (topology)In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
") is the circle S1, described by the equality x02 + x12 = 1. If a balloonBalloonA balloon is an inflatable flexible bag filled with a gas, such as helium, hydrogen, nitrous oxide, oxygen, or air. Modern balloons can be made from materials such as rubber, latex, polychloroprene, or a nylon fabric, while some early balloons were made of dried animal bladders, such as the pig...
is punctured and spread flat it produces a disk; this construction repairs the puncture, like pulling a drawstring. The slashSlash (punctuation)The slash is a sign used as a punctuation mark and for various other purposes. It is now often called a forward slash , and many other alternative names.-History:...
, pronounced "modulo", means to take the topological space on the left (the disk) and in it join together as one all the points on the right (the circle). The region is 2-dimensional, which is why topology calls the resulting topological space a 2-sphere. Generalized, Dn/Sn−1 produces Sn. For example, D1 is a line segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
, and the construction joins its ends to make a circle. An equivalent description is that the boundary of an n-dimensional disk is glued to a point, producing a CW complexCW complexIn topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
.- Suspension of equator: written in topology as ΣS1
- This construction, though simple, is of great theoretical importance. Take the circle S1 to be the equatorEquatorAn equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
, and sweep each point on it to one point above (the North Pole), producing the northern hemisphere, and to one point below (the South Pole), producing the southern hemisphere. For each positive integer n, the n-sphere x02 + x12 + ⋯ + xn2 = 1 has as equator the (n − 1)-sphere x02 + x12 + ⋯ + xn−12 = 1, and the suspension ΣSn−1 produces Sn.
Some theory requires selecting a fixed point on the sphere, calling the pair (sphere, point) a pointed sphere
Pointed space
In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
. For some spaces the choice matters, but for a sphere all points are equivalent so the choice is a matter of convenience. The point (1, 0, 0, …, 0), which is on the equator of all the spheres, works well for geometric spheres; the (collapsed) rim of the disk is another obvious choice.
Homotopy group


Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is its continuity structure, formalized in terms of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s or neighborhoods. A continuous map is a function between spaces that preserves continuity. A homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
is a continuous path between continuous maps; two maps connected by a homotopy are said to be homotopic. The idea common to all these concepts is to discard variations that do not affect outcomes of interest. An important practical example is the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, where "closed curves" are continuous maps from the circle into the complex plane, and where two closed curves produce the same integral result if they are homotopic in the topological space consisting of the plane minus the points of singularity.
The first homotopy group, or fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, π1(X) of a (path connected) topological space X thus begins with continuous maps from a pointed circle (S1,s) to the pointed space (X,x), where maps from one pair to another map s into x. These maps (or equivalently, closed curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s) are grouped together into equivalence classes based on homotopy (keeping the "base point" x fixed), so that two maps are in the same class if they are homotopic. Just as one point is distinguished, so one class is distinguished: all maps (or curves) homotopic to the constant map S1↦x are called null homotopic. The classes become an abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
ic group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with the introduction of addition, defined via an "equator pinch". This pinch maps the equator of a pointed sphere (here a circle) to the distinguished point, producing a "bouquet of spheres" — two pointed spheres joined at their distinguished point. The two maps to be added map the upper and lower spheres separately, agreeing on the distinguished point, and composition with the pinch gives the sum map.
More generally, the i-th homotopy group, πi(X) begins with the pointed i-sphere (Si,s), and otherwise follows the same procedure. The null homotopic class acts as the identity of the group addition, and for X equal to Sn (for positive n) — the homotopy groups of spheres — the groups are abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
and finitely generated. If for some i all maps are null homotopic, then the group πi consists of one element, and is called the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
.
A continuous map between two topological spaces induces a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
between the associated homotopy groups. In particular, if the map is a continuous bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
(a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
), so that the two spaces have the same topology, then their i-th homotopy groups are isomorphic for all i. However, the real plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
has exactly the same homotopy groups as a solitary point (as does a Euclidean space of any dimension), and the real plane with a point removed has the same groups as a circle, so groups alone are not enough to distinguish spaces. Although the loss of discrimination power is unfortunate, it can also make certain computations easier.
Low-dimensional examples
The low-dimensional examples of homotopy groups of spheres provide a sense of the subject, because these special cases can be visualized in ordinary 3-dimensional space . However, such visualizations are not mathematical proofs, and do not capture the possible complexity of maps between spheres.π1(S1) = Z

Rubber band
A rubber band is a short length of rubber and latex formed in the shape of a loop and is commonly used to hold multiple objects together...
around one's finger: it can be wrapped once, twice, three times and so on. The wrapping can be in either of two directions, and wrappings in opposite directions will cancel out after a deformation. The homotopy group π1(S1) is therefore an infinite cyclic group, and is isomorphic to the group Z of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s under addition: a homotopy class is identified with an integer by counting the number of times a mapping in the homotopy class wraps around the circle. This integer can also be thought of as the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of a loop around the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
in the plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
.
The identification (a group isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
) of the homotopy group with the integers is often written
Abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
as an equality: thus π1(S1) = Z.
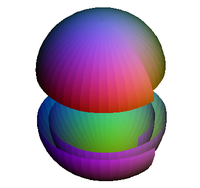
π2(S2) = Z
Mappings from a 2-sphere to a 2-sphere can be visualized as wrapping a plastic bag around a ball and then sealing it. The sealed bag is topologically equivalent to a 2-sphere, as is the surface of the ball. The bag can be wrapped more than once by twisting it and wrapping it back over the ball. (There is no requirement for the continuous map to be injective and so the bag is allowed to pass through itself.) The twist can be in one of two directions and opposite twists can cancel out by deformation. The total number of twists after cancellation is an integer, called the degree of the mapping. As in the case mappings from the circle to the circle, this degree identifies the homotopy group with the group of integers, Z.These two results generalize: for all n > 0, πn(Sn) = Z (see below).
π1(S2) = 0

Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
, with only one element, the identity element, and so it can be identified with the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of Z consisting only of the number zero. This group is often denoted by 0.
This result generalises to higher dimensions. All mappings from a lower-dimensional sphere into a sphere of higher dimension are similarly trivial: if i < n, then πi(Sn) = 0.
π2(S1) = 0
All the interesting cases of homotopy groups of spheres involve mappings from a higher-dimensional sphere onto one of lower dimension. Unfortunately, the only example which can easily be visualized is not interesting: there are no nontrivial mappings from the ordinary sphere to the circle. Hence, π2(S1) = 0. This is because S1 has the real line as its universal cover which is contractible (it has the homotopy type of a point). In addition, because S2 is simply connected, by the lifting criterion, any map from S2 to S1 can be lifted to a map into the real line and the nullhomotopy descends to the downstairs space.π3(S2) = Z
The first nontrivial example with i > n concerns mappings from the 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
to the ordinary 2-sphere, and was discovered by Heinz Hopf
Heinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
, who constructed a nontrivial map from S3 to S2, now known as the Hopf fibration . This map generates
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
the homotopy group π3(S2) = Z.
History
In the late 19th century Camille JordanCamille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
introduced the notion of homotopy and used the notion of a homotopy group, without using the language of group theory . A more rigorous approach was adopted by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
in his 1895 set of papers Analysis situs where the related concepts of homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
and the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
were also introduced .
Higher homotopy groups were first defined by Eduard Čech
Eduard Cech
Eduard Čech was a Czech mathematician born in Stračov, Bohemia . His research interests included projective differential geometry and topology. In 1921–1922 he collaborated with Guido Fubini in Turin...
in 1932 . (His first paper was withdrawn on the advice of Pavel Sergeyevich Alexandrov and Heinz Hopf, on the grounds that the groups were commutative so could not be the right generalizations of the fundamental group.) Witold Hurewicz
Witold Hurewicz
Witold Hurewicz was a Polish mathematician.- Early life and education :Witold Hurewicz was born to a Jewish family in Łódź, Russian Empire ....
is also credited with the introduction of homotopy groups in his 1935 paper and also for the Hurewicz theorem
Hurewicz theorem
In mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism...
which can be used to calculate some of the groups .
An important method for calculating the various groups is the concept of stable algebraic topology, which finds properties that are independent of the dimensions. Typically these only hold for larger dimensions. The first such result was Hans Freudenthal
Hans Freudenthal
Hans Freudenthal was a Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education....
's suspension theorem
Freudenthal suspension theorem
In mathematics, and specifically in the field of homotopy theory, the Freudenthal suspension theorem is the fundamental result leading to the concept of stabilization of homotopy groups and ultimately to stable homotopy theory. It explains the behavior of simultaneously taking suspensions and...
, published in 1937. Stable algebraic topology flourished between 1945 and 1966 with many important results . In 1953 George W. Whitehead
George W. Whitehead
George William Whitehead, Jr. was a professor of mathematics at the Massachusetts Institute of Technology, a member of the United States National Academy of Sciences, and a Fellow of the American Academy of Arts and Sciences. He is known for his work on algebraic topology...
showed that there is a metastable range for the homotopy groups of spheres. Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
used spectral sequences to show that most of these groups are finite, the exceptions being πn(Sn) and π4n−1(S2n). Others who worked in this area included José Ádem
José Ádem
José Ádem Chaín was a Mexican mathematician who worked inalgebraic topology, and proved the Ádem relations between Steenrod squares....
, Hiroshi Toda
Hiroshi Toda
is a Japanese mathematician, who specializes in stable and unstable homotopy theory.He started publishing in 1952. Many of his early papers are concerned with the study of Whitehead products and their behaviour under suspension and more generally with the homotopy groups of spheres. In a 1957...
, Frank Adams
Frank Adams
John Frank Adams FRS was a British mathematician, one of the founders of homotopy theory.-Life:He was born in Woolwich, a suburb in south-east London. He began research as a student of Abram Besicovitch, but soon switched to algebraic topology. He received his Ph.D. from the University of...
and J. Peter May
J. Peter May
Jon Peter May is an American mathematician, working in the fields of algebraic topology, category theory, homotopy theory, and the foundational aspects of spectra. He is known, in particular, for inventing the term operads and the May spectral sequence.He received a B.A. from Swarthmore College in...
. The stable homotopy groups πn+k(Sn) are known for k up to 64, and, as of 2007, unknown for larger k .
General theory
As noted already, when i is less than n, πi(Sn) = 0, the trivial groupTrivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
. The reason is that a continuous mapping from an i-sphere to an n-sphere with i < n can always be deformed so that it is not surjective. Consequently, its image is contained in Sn with a point removed; this is a contractible space
Contractible space
In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
, and any mapping to such a space can be deformed into a one-point mapping.
The case i = n has also been noted already, and is an easy consequence of the Hurewicz theorem
Hurewicz theorem
In mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism...
: this theorem links homotopy groups with homology groups, which are generally easier to calculate; in particular, it shows that for a simply-connected space X, the first nonzero homotopy group πk(X), with k > 0, is isomorphic to the first nonzero homology group Hk(X). For the n-sphere, this immediately implies that for n > 0, πn(Sn) = Hn(Sn) = Z.
The homology groups Hi(Sn), with i > n, are all trivial. It therefore came as a great surprise historically that the corresponding homotopy groups are not trivial in general. This is the case that is of real importance: the higher homotopy groups πi(Sn), for i > n, are surprisingly complex and difficult to compute, and the effort to compute them has generated a significant amount of new mathematics.
Table
The following table of gives an idea of the complexity of the higher homotopy groups even for spheres of dimension 8 or less. In this table, the entries are either the trivial groupTrivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
0, the infinite cyclic group Z, finite cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of order n (written as Zn), or direct products
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of such groups (written, for example, as Z24×Z3 or Z22 = Z2×Z2). Extended tables of homotopy groups of spheres are given at the end of the article.
| π1 | π2 | π3 | π4 | π5 | π6 | π7 | π8 | π9 | π10 | π11 | π12 | π13 | π14 | π15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| S1 | Z | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| S2 | 0 | Z | Z | Z2 | Z2 | Z12 | Z2 | Z2 | Z3 | Z15 | Z2 | Z22 | Z12×Z2 | Z84×Z22 | Z22 |
| S3 | 0 | 0 | Z | Z2 | Z2 | Z12 | Z2 | Z2 | Z3 | Z15 | Z2 | Z22 | Z12×Z2 | Z84×Z22 | Z22 |
| S4 | 0 | 0 | 0 | Z | Z2 | Z2 | Z×Z12 | Z22 | Z22 | Z24×Z3 | Z15 | Z2 | Z23 | Z120×Z12×Z2 | Z84×Z25 |
| S5 | 0 | 0 | 0 | 0 | Z | Z2 | Z2 | Z24 | Z2 | Z2 | Z2 | Z30 | Z2 | Z23 | Z72×Z2 |
| S6 | 0 | 0 | 0 | 0 | 0 | Z | Z2 | Z2 | Z24 | 0 | Z | Z2 | Z60 | Z24×Z2 | Z23 |
| S7 | 0 | 0 | 0 | 0 | 0 | 0 | Z | Z2 | Z2 | Z24 | 0 | 0 | Z2 | Z120 | Z23 |
| S8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Z | Z2 | Z2 | Z24 | 0 | 0 | Z2 | Z×Z120 |
The first two rows of this table are straightforward. The homotopy groups πi(S0) of the 0-dimensional sphere are trivial for i > 0, because any base point preserving map from an i-sphere to a 0-sphere is a one-point mapping. Similarly, the homotopy groups πi(S1) of the 1-sphere are trivial for i > 1, because the universal covering space, R, which has the same higher homotopy groups, is contractible.
Beyond these two rows, the higher homotopy groups (i > n) appear to be chaotic, but in fact there are many patterns, some obvious and some very subtle.
- The groups below the jagged black line are constant along the diagonals (as indicated by the red, green and blue coloring).
- Most of the groups are finite. The only unstable groups which are not are either on the main diagonal or immediately above the jagged line (highlighted in yellow).
- The third and fourth rows of the table are the same starting in the third column (i.e., πi(S2) = πi(S3) for ). This isomorphism is induced by the Hopf fibration .
These patterns follow from many different theoretical results.
Stable and unstable groups
The fact that the groups below the jagged line in the table above are constant along the diagonals is explained by the suspension theoremFreudenthal suspension theorem
In mathematics, and specifically in the field of homotopy theory, the Freudenthal suspension theorem is the fundamental result leading to the concept of stabilization of homotopy groups and ultimately to stable homotopy theory. It explains the behavior of simultaneously taking suspensions and...
of Hans Freudenthal
Hans Freudenthal
Hans Freudenthal was a Dutch mathematician. He made substantial contributions to algebraic topology and also took an interest in literature, philosophy, history and mathematics education....
, which implies that the suspension homomorphism from πn+k(Sn) to πn+k+1(Sn+1) is an isomorphism for n > k + 1. The groups πn+k(Sn) with n > k + 1 are called the stable homotopy groups of spheres, and are denoted πkS: they are finite abelian groups for k ≠ 0, and have been computed in numerous cases, although the general pattern is still elusive. . For n ≤ k+1, the groups are called the unstable homotopy groups of spheres.
Hopf fibrations
The classical Hopf fibration is a fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
:

The general theory of fiber bundles F→E→B shows that there is a long exact sequence of homotopy groups

For this specific bundle, each group homomorphism πi(S1)→πi(S3), induced by the inclusion S1→S3, maps all of πi(S1) to zero, since the lower dimensional sphere S1 can be deformed to a point inside the higher dimensional one S3. This corresponds to the vanishing of π1(S3). Thus the long exact sequence breaks into short exact sequences,
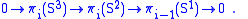
Since Sn+1 is a suspension of Sn, these sequences are split
Splitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
by the suspension homomorphism
Freudenthal suspension theorem
In mathematics, and specifically in the field of homotopy theory, the Freudenthal suspension theorem is the fundamental result leading to the concept of stabilization of homotopy groups and ultimately to stable homotopy theory. It explains the behavior of simultaneously taking suspensions and...
πi−1(S1)→πi(S2), giving isomorphisms

Since πi−1(S1) vanishes for i at least 3, the first row shows that πi(S2) and πi(S3) are isomorphic whenever i is at least 3, as observed above.
The Hopf fibration may be constructed as follows: pairs of complex numbers (z0,z1) with |z0|2 + |z1|2 = 1 form a 3-sphere, and their ratios z0/z1 cover the complex plane plus infinity
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, a 2-sphere. The Hopf map S3 → S2 sends any such pair to its ratio.
Similarly, there are generalized Hopf fibrations


constructed using pairs of quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s or octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s instead of complex numbers . Here, too, π3(S7) and π7(S15) are zero. Thus the long exact sequences again break into families of split short exact sequences, implying two families of relations.
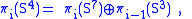
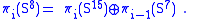
The three fibrations have base space Sn with n = 2m, for m = 1, 2, 3. A fibration does exist for S1 (m = 0), but not for S16 (m = 4) and beyond. Although generalizations of the relations to S16 are often true, they sometimes fail; for example,
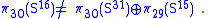
There can be no fibration

the first non-trivial case of the Hopf invariant
Hopf invariant
In mathematics, in particular in algebraic topology, the Hopf invariant is a homotopy invariant of certain maps between spheres.- Motivation :In 1931 Heinz Hopf used Clifford parallels to construct the Hopf map\eta\colon S^3 \to S^2,...
one problem, because such a fibration would imply that the failed relation is true.
Framed cobordism
Homotopy groups of spheres are closely related to cobordismCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
classes of manifolds.
In 1938 Lev Pontrjagin established an isomorphism between the homotopy group πn+k(Sn) and the group Ωkframed(Sn+k) of cobordism classes of differentiable k-submanifolds of Sn+k which are `framed', i.e. have a trivialized normal bundle
Normal bundle
In differential geometry, a field of mathematics, a normal bundle is a particular kind of vector bundle, complementary to the tangent bundle, and coming from an embedding .-Riemannian manifold:...
. Every map ƒ:Sn+k → Sn is homotopic to a differentiable map with
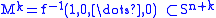 a framed k-dimensional submanifold. For example, πn(Sn)=Z is the cobordism group of framed 0-dimensional submanifolds of Sn, computed by the algebraic sum of their points, corresponding to the degree of maps
a framed k-dimensional submanifold. For example, πn(Sn)=Z is the cobordism group of framed 0-dimensional submanifolds of Sn, computed by the algebraic sum of their points, corresponding to the degree of maps  . The projection of the Hopf fibration
. The projection of the Hopf fibration 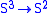 represents a generator of π3(S2) = Ω1framed(S3)=Z which corresponds to the framed 1-dimensional submanifold of S3 defined by the standard embedding
represents a generator of π3(S2) = Ω1framed(S3)=Z which corresponds to the framed 1-dimensional submanifold of S3 defined by the standard embedding  with a nonstandard trivialization of the normal 2-plane bundle. Until the advent of more sophisticated algebraic methods in the early 1950s (Serre) the Pontrjagin isomorphism was the main tool for computing the homotopy groups of spheres. In 1954 the Pontrjagin isomorphism was generalized by René Thom
with a nonstandard trivialization of the normal 2-plane bundle. Until the advent of more sophisticated algebraic methods in the early 1950s (Serre) the Pontrjagin isomorphism was the main tool for computing the homotopy groups of spheres. In 1954 the Pontrjagin isomorphism was generalized by René ThomRené Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
to an isomorphism expressing other groups of cobordism classes (e.g. of all manifolds) as homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of spaces and spectra
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
. In more recent work the argument is usually reversed, with cobordism groups computed in terms of homotopy groups .
Finiteness and torsion
In 1951, Jean-Pierre SerreJean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
showed that homotopy groups of spheres are all finite except for those of the form πn(Sn) or π4n−1(S2n) (for positive n), when the group is the product of the infinite cyclic group with a finite abelian group . In particular the homotopy groups are determined by their p-components for all primes p. The 2-components are hardest to calculate, and in several ways behave differently from the p-components for odd primes.
In the same paper, Serre found the first place that p-torsion occurs in the homotopy groups of n dimensional spheres, by showing that πn+k(Sn) has no p-torsion if k < 2p − 3, and has a unique subgroup of order p if n ≥ 3 and k = 2p − 3. The case of 2-dimensional spheres is slightly different: the first p-torsion occurs for k = 2p − 3 + 1. In the case of odd torsion there are more precise results; in this case there is a big difference between odd and even dimensional spheres. If p is an odd prime and n = 2i + 1 is odd, then elements of the p-component
Component (group theory)
In mathematics, in the field of group theory, a component of a finite group is a quasisimple subnormal subgroup. Any two distinct components commute...
of πn+k(Sn) have order at most pi . This is in some sense the best possible result, as these groups are known to have elements of this order for some values of k . Furthermore, the stable range can be extended in this case: if n is odd then the double suspension from πk(Sn) to πk+2(Sn+2) is an isomorphism of p-components if k < p(n + 1) − 3, and an epimorphism if equality holds . The p-torsion of the intermediate group πk+1(Sn+1) can be strictly larger.
The results above about odd torsion only hold for odd-dimensional spheres: for even-dimensional spheres, the James fibration gives the torsion at odd primes p in terms of that of odd-dimensional spheres,

(where (p) means take the p-component) . This exact sequence is similar to the ones coming from the Hopf fibration; the difference is that it works for all even-dimensional spheres, albeit at the expense of ignoring 2-torsion. Combining the results for odd and even dimensional spheres shows that much of the odd torsion of unstable homotopy groups is determined by the odd torsion of the stable homotopy groups.
For stable homotopy groups there are more precise results about p-torsion. For example, if k < 2p(p − 1) − 2 for a prime p then the p-primary component of the stable homotopy group πkS vanishes unless k + 1 is divisible by 2(p − 1), in which case it is cyclic of order p .
The J-homomorphism
An important subgroup of πn+k(Sn), for k ≥ 2, is the image of the J-homomorphismJ-homomorphism
In mathematics, the J-homomorphism is a mapping from the homotopy groups of the special orthogonal groups to the homotopy groups of spheres. It was defined by , extending a construction of .-Definition:...
J: πk(SO(n)) → πn+k(Sn), where SO(n) denotes the special orthogonal group . In the stable range n ≥ k+2, the homotopy groups πk(SO(n)) only depend on k modulo 8. This period 8 pattern is known as Bott periodicity, and it is reflected in the stable homotopy groups of spheres via the image of the J-homomorphism which is:
- a cyclic group of order 2 if k is congruentCongruence relationIn abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
to 0 or 1 moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
8; - trivial if k is congruent to 2, 4, 5, or 6 modulo 8; and
- a cyclic group of order equal to the denominator of B2n/4n, where B2n is a Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
, if k ≡ 3 (mod 4).
This last case accounts for the elements of unusually large finite order in πn+k(Sn) for such values of k. For example, the stable groups πn+11(Sn) have a cyclic subgroup of order 504, the denominator of B6/12 = 1⁄504.
The stable homotopy groups of spheres are the direct sum of the image of the J-homomorphism, and the kernel of the Adams e-invariant, a homomorphism from these groups to Q/Z. Roughly speaking, the image of the J-homomorphism is the subgroup of "well understood" or "easy" elements of the stable homotopy groups. These well understood elements account for most elements of the stable homotopy groups of spheres in small dimensions. The quotient of πnS by the image of the J-homomorphism is considered to be the "hard" part of the stable homotopy groups of spheres . (Adams also introduced certain order 2 elements μn of πnS for n = 1 or 2 mod 8, and these are also considered to be "well understood".) Tables of homotopy groups of spheres sometimes omit the "easy" part Im(J) to save space.
Ring structure
The direct sum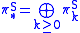
of the stable homotopy groups of spheres is a supercommutative graded ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, where multiplication is given by composition of representing maps, and any element of non-zero degree is nilpotent
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
.
Example: If η is the generator of π1S (of order 2),
then η2 is nonzero and generates π2S, and η3 is nonzero and 12 times a generator of π3S, while η4 is zero because the group π4S is trivial.
If f and g and h are elements of π∗S with f⋅g = 0 and g⋅h = 0, there is a Toda bracket
Toda bracket
In mathematics, the Toda bracket is an operation on homotopy classes of maps, in particular on homotopy groups of spheres, named after Hiroshi Toda who defined them and used them to compute homotopy groups of spheres in .- Definition :See or for more information....
〈f,g,h〉 of these elements . The Toda bracket is not quite an element of a stable homotopy group, because it is only defined up to addition of products of certain other elements. Hiroshi Toda
Hiroshi Toda
is a Japanese mathematician, who specializes in stable and unstable homotopy theory.He started publishing in 1952. Many of his early papers are concerned with the study of Whitehead products and their behaviour under suspension and more generally with the homotopy groups of spheres. In a 1957...
used the composition product and Toda brackets to label many of the elements of homotopy groups. There are also higher Toda brackets of several elements, defined when suitable lower Toda brackets vanish. This parallels the theory of Massey product
Massey product
In algebraic topology, the Massey product is a cohomology operation of higher order introduced in , which generalizes the cup product.-Massey triple product:...
s in cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
.
Every element of the stable homotopy groups of spheres can be expressed using composition products and higher Toda brackets in terms of certain well known elements, called Hopf elements .
Computational methods
If X is any finite simplicial complex with finite fundamental group, in particular if X is a sphere of dimension at least 2, then its homotopy groups are all finitely generated abelian groupFinitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
s. To compute these groups, they are often factored into their p-components
Component (group theory)
In mathematics, in the field of group theory, a component of a finite group is a quasisimple subnormal subgroup. Any two distinct components commute...
for each prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, and calculating each of these p-groups
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
separately. The first few homotopy groups of spheres can be computed using ad hoc variations of the ideas above; beyond this point, most methods for computing homotopy groups of spheres are based on spectral sequence
Spectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
s . This is usually done by constructing suitable fibrations and taking the associated long exact sequences of homotopy groups; spectral sequences are a systematic way of organizing the complicated information that this process generates.
- "The method of killing homotopy groups", due to involves repeatedly using the Hurewicz theoremHurewicz theoremIn mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism...
to compute the first non-trivial homotopy group and then killing (eliminating) it with a fibration involving an Eilenberg-MacLane spaceEilenberg-MacLane spaceIn mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
. In principle this gives an effective algorithm for computing all homotopy groups of any finite simply connected simplicial complex, but in practice it is too cumbersome to use for computing anything other than the first few nontrivial homotopy groups as the simplicial complex becomes much more complicated every time one kills a homotopy group.
- The Serre spectral sequenceSerre spectral sequenceIn mathematics, the Serre spectral sequence is an important tool in algebraic topology...
was used by Serre to prove some of the results mentioned previously. He used the fact that taking the loop space of a well behaved space shifts all the homotopy groups down by 1, so the nth homotopy group of a space X is the first homotopy group of its (n−1)-fold repeated loop space, which is equal to the first homology group of the (n−1)-fold loop space by the Hurewicz theorem. This reduces the calculation of homotopy groups of X to the calculation of homology groups of its repeated loop spaces. The Serre spectral sequence relates the homology of a space to that of its loop space, so can sometimes be used to calculate the homology of loop spaces. The Serre spectral sequence tends to have many non-zero differentials, which are hard to control, and too many ambiguities appear for higher homotopy groups. Consequently, it has been superseded by more powerful spectral sequences with fewer non-zero differentials, which give more information. - The EHP spectral sequenceEHP spectral sequenceIn mathematics, the EHP spectral sequence is a spectral sequence used for inductively calculating the homotopy groups of sphereslocalized at some prime p. It is described in more detail in and...
can be used to recursively calculate the homotopy groups of spheres, and is based on some fibrations used by Toda in his calculations of homotopy groups . - The classical Adams spectral sequenceAdams spectral sequenceIn mathematics, the Adams spectral sequence is a spectral sequence introduced by . Like all spectral sequences, it is a computational tool; it relates homology theory to what is now called stable homotopy theory...
has E2 term given by the Ext groups ExtA(p)∗,∗(Zp,Zp) over the mod p Steenrod algebraSteenrod algebraIn algebraic topology, a Steenrod algebra was defined by to be the algebra of stable cohomology operations for mod p cohomology.For a given prime number p, the Steenrod algebra Ap is the graded Hopf algebra over the field Fp of order p, consisting of all stable cohomology operations for mod p...
A(p), and converges to something closely related to the p-component of the stable homotopy groups. The initial terms of the Adams spectral sequence are themselves quite hard to compute: this is sometimes done using an auxiliary spectral sequence called the May spectral sequenceMay spectral sequenceIn mathematics, the May spectral sequence is a spectral sequence, introduced by , used for calculating the initial term of the Adams spectral sequence, which is in turn used for calculating the stable homotopy groups of spheres. It is described in detail in ....
. - The Adams–Novikov spectral sequence is a more powerful version of the Adams spectral sequence replacing ordinary cohomology mod p with a generalized cohomology theory, such as complex cobordismComplex cobordismIn mathematics, complex cobordism is a generalized cohomology theory related to cobordism of manifolds. Its spectrum is denoted by MU. It is an exceptionally powerful cohomology theory, but can be quite hard to compute, so often instead of using it directly one uses some slightly weaker theories...
or, more usually, a piece of it called Brown–Peterson cohomologyBrown–Peterson cohomologyIn mathematics, Brown–Peterson cohomology is a generalized cohomology theory introduced by, depending on a choice of prime p. It is described in detail by .Its representing spectrum is denoted by BP.-Complex cobordism and Quillen's idempotent:...
. The initial term is again quite hard to calculate; to do this one can use the chromatic spectral sequenceChromatic spectral sequenceIn mathematics, the chromatic spectral sequence is a spectral sequence, introduced by , used for calculating the initial term of the Adams–Novikov spectral sequence for BP cohomology, which is in turn used for calculating the stable homotopy groups of spheres....
.

- A variation of this last approach uses a backwards version of the Adams–Novikov spectral sequence for Brown–Peterson cohomology: the limit is known, and the initial terms involve unknown stable homotopy groups of spheres that one is trying to find. used this approach to calculate the 2-components of the first 64 stable homotopy groups; unfortunately there was a mistake in his calculations for the 54th stem and beyond, which was corrected by .
The computation of the homotopy groups of S2 has been reduced to a combinatorial group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
question. identify these homotopy groups as certain quotients of the Brunnian
Brunnian link
In knot theory, a branch of mathematics, a Brunnian link is a nontrivial link that becomes trivial if any component is removed. In other words, cutting any loop frees all the other loops ....
braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s of S2. Under this correspondence, every nontrivial element in πn(S2) for n > 2 may be represented by a Brunnian braid
Braid
A braid is a complex structure or pattern formed by intertwining three or more strands of flexible material such as textile fibres, wire, or human hair...
over S2 that is not Brunnian over the disk D2. For example, the Hopf map S3 → S2 corresponds to the Borromean rings
Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
.
Applications
- The winding numberWinding numberIn mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
(corresponding to an integer of π1(S1) = Z) can be used to prove the fundamental theorem of algebraFundamental theorem of algebraThe fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
, which states that every non-constant complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
has a zero. - The fact that πn−1(Sn−1) = Z implies the Brouwer fixed point theoremBrouwer fixed point theoremBrouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
that every continuous map from the n-dimensional ballBall (mathematics)In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
to itself has a fixed point. - The stable homotopy groups of spheres are important in singularity theorySingularity theory-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
, which studies the structure of singular points of smooth maps or algebraic varieties. Such singularities arise as critical pointCritical point (mathematics)In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s of smooth maps from Rm to Rn. The geometry near a critical point of such a map can be described by an element of πm−1(Sn−1), by considering the way in which a small m − 1 sphere around the critical point maps into a topological n − 1 sphere around the critical valueCritical value-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...
. - The fact that the third stable homotopy group of spheres is cyclic of order 24, first proved by Vladimir Rokhlin, implies Rokhlin's theoremRokhlin's theoremIn 4-dimensional topology, a branch of mathematics, Rokhlin's theorem states that if a smooth, compact 4-manifold M has a spin structure , then the signature of its intersection form, a quadratic form on the second cohomology group H2, is divisible by 16...
that the signatureSignature (topology)In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
of a compact smooth spinSpin structureIn differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
4-manifold4-manifoldIn mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
is divisible by 16 . - Stable homotopy groups of spheres are used to describe the group Θn of h-cobordismH-cobordismA cobordism W between M and N is an h-cobordism if the inclusion mapsare homotopy equivalences...
classes of oriented homotopy n-spheres (for n ≠ 4, this is the group of smooth structureSmooth structureIn mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
s on n-spheres, up to orientation-preserving diffeomorphism; the non-trivial elements of this group are represented by exotic sphereExotic sphereIn differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s). More precisely, there is an injective map
>
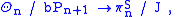 where bPn+1 is the cyclic subgroup represented by homotopy spheres that bound a parallelizable manifold, πnS is the nth stable homotopy group of spheres, and J is the image of the J-homomorphism. This is an isomorphism unless n is of the form 2k−2, in which case the image has index 1 or 2 .
where bPn+1 is the cyclic subgroup represented by homotopy spheres that bound a parallelizable manifold, πnS is the nth stable homotopy group of spheres, and J is the image of the J-homomorphism. This is an isomorphism unless n is of the form 2k−2, in which case the image has index 1 or 2 .
- The groups Θn above, and therefore the stable homotopy groups of spheres, are used in the classification of possible smooth structures on a topological or piecewise linear manifoldPiecewise linear manifoldIn mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions.An isomorphism of PL manifolds is called a PL...
. - The Kervaire invariant problem, about the existence of manifolds of Kervaire invariant 1 in dimensions 2k − 2 can be reduced to a question about stable homotopy groups of spheres. For example, knowledge of stable homotopy groups of degree up to 48 has been used to settle the Kervaire invariant problem in dimension 26 − 2 = 62 . (This was the smallest value of k for which the question was open at the time.)
- The stable homotopy groups of the spheres have been interpreted in terms of the plus constructionPlus constructionIn mathematics, the plus construction is a method for simplifying the fundamental group of a space without changing its homology and cohomology groups. It was introduced by Daniel Quillen. Given a perfect normal subgroup of the fundamental group of a connected CW complex X, attach two-cells along...
applied to the classifying spaceClassifying spaceIn mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
of the symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, leading to an identification of K-theory of the field with one elementField with one elementIn mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
with stable homotopy groups .
Table of homotopy groups
Tables of homotopy groups of spheres are most conveniently organized by showing πn+k(Sn).The following table shows many of the groups πn+k(Sn). (These tables are based on the table of homotopy groups of spheres in .) The stable homotopy groups are highlighted in blue, the unstable ones in red. Each homotopy group is the product of the cyclic groups of the orders given in the table, using the following conventions:
- The entry "⋅" denotes the trivial group.
- Where the entry is an integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
, m, the homotopy group is the cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of that order (generally written Zm). - Where the entry is ∞, the homotopy group is the infinite cyclic group, Z.
- Where entry is a product, the homotopy group is the cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
(equivalently, direct sum) of the cyclic groups of those orders. Powers indicate repeated products. (Note that when a and b have no common factor, Za×Zb is isomorphic to Zab.)
Example: π19(S10) = π9+10(S10) = Z×Z2×Z2×Z2, which is denoted by ∞⋅23 in the table.
| Sn → | S0 | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S≥13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| π<n(Sn) | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | |
| π0+n(Sn) | 2 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| π1+n(Sn) | ⋅ | ⋅ | ∞ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| π2+n(Sn) | ⋅ | ⋅ | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| π3+n(Sn) | ⋅ | ⋅ | 2 | 12 | ∞⋅12 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
| π4+n(Sn) | ⋅ | ⋅ | 12 | 2 | 22 | 2 | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ |
| π5+n(Sn) | ⋅ | ⋅ | 2 | 2 | 22 | 2 | ∞ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ |
| π6+n(Sn) | ⋅ | ⋅ | 2 | 3 | 24⋅3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| π7+n(Sn) | ⋅ | ⋅ | 3 | 15 | 15 | 30 | 60 | 120 | ∞⋅120 | 240 | 240 | 240 | 240 | 240 |
| π8+n(Sn) | ⋅ | ⋅ | 15 | 2 | 2 | 2 | 24⋅2 | 23 | 24 | 23 | 22 | 22 | 22 | 22 |
| π9+n(Sn) | ⋅ | ⋅ | 2 | 22 | 23 | 23 | 23 | 24 | 25 | 24 | ∞⋅23 | 23 | 23 | 23 |
| π10+n(Sn) | ⋅ | ⋅ | 22 | 12⋅2 | 120⋅12⋅2 | 72⋅2 | 72⋅2 | 24⋅2 | 242⋅2 | 24⋅2 | 12⋅2 | 6⋅2 | 6 | 6 |
| π11+n(Sn) | ⋅ | ⋅ | 12⋅2 | 84⋅22 | 84⋅25 | 504⋅22 | 504⋅4 | 504⋅2 | 504⋅2 | 504⋅2 | 504 | 504 | ∞⋅504 | 504 |
| π12+n(Sn) | ⋅ | ⋅ | 84⋅22 | 22 | 26 | 23 | 240 | ⋅ | ⋅ | ⋅ | 12 | 2 | 22 | See below |
| π13+n(Sn) | ⋅ | ⋅ | 22 | 6 | 24⋅6⋅2 | 6⋅2 | 6 | 6 | 6⋅2 | 6 | 6 | 6⋅2 | 6⋅2 | |
| π14+n(Sn) | ⋅ | ⋅ | 6 | 30 | 2520⋅6⋅2 | 6⋅2 | 12⋅2 | 24⋅4 | 240⋅24⋅4 | 16⋅4 | 16⋅2 | 16⋅2 | 48⋅4⋅2 | |
| π15+n(Sn) | ⋅ | ⋅ | 30 | 30 | 30 | 30⋅2 | 60⋅6 | 120⋅23 | 120⋅25 | 240⋅23 | 240⋅22 | 240⋅2 | 240⋅2 | |
| π16+n(Sn) | ⋅ | ⋅ | 30 | 6⋅2 | 62⋅2 | 22 | 504⋅22 | 24 | 27 | 24 | 240⋅2 | 2 | 2 | |
| π17+n(Sn) | ⋅ | ⋅ | 6⋅2 | 12⋅22 | 24⋅12⋅4⋅22 | 4⋅22 | 24 | 24 | 6⋅24 | 24 | 23 | 23 | 24 | |
| π18+n(Sn) | ⋅ | ⋅ | 12⋅22 | 12⋅22 | 120⋅12⋅25 | 24⋅22 | 24⋅6⋅2 | 24⋅2 | 504⋅24⋅2 | 24⋅2 | 24⋅22 | 8⋅4⋅2 | 480⋅42⋅2 | |
| π19+n(Sn) | ⋅ | ⋅ | 12⋅22 | 132⋅2 | 132⋅25 | 264⋅2 | 1056⋅8 | 264⋅2 | 264⋅2 | 264⋅2 | 264⋅6 | 264⋅23 | 264⋅25 |
| Sn → | S13 | S14 | S15 | S16 | S17 | S18 | S19 | S20 | S≥21 |
|---|---|---|---|---|---|---|---|---|---|
| π12+n(Sn) | 2 | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ | ⋅ |
| π13+n(Sn) | 6 | ∞⋅3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| π14+n(Sn) | 16⋅2 | 8⋅2 | 4⋅2 | 22 | 22 | 22 | 22 | 22 | 22 |
| π15+n(Sn) | 480⋅2 | 480⋅2 | 480⋅2 | ∞⋅480⋅2 | 480⋅2 | 480⋅2 | 480⋅2 | 480⋅2 | 480⋅2 |
| π16+n(Sn) | 2 | 24⋅2 | 23 | 24 | 23 | 22 | 22 | 22 | 22 |
| π17+n(Sn) | 24 | 24 | 25 | 26 | 25 | ∞⋅24 | 24 | 24 | 24 |
| π18+n(Sn) | 82⋅2 | 82⋅2 | 82⋅2 | 24⋅82⋅2 | 82⋅2 | 8⋅4⋅2 | 8⋅22 | 8⋅2 | 8⋅2 |
| π19+n(Sn) | 264⋅23 | 264⋅4⋅2 | 264⋅22 | 264⋅22 | 264⋅22 | 264⋅2 | 264⋅2 | ∞⋅264⋅2 | 264⋅2 |
Table of stable homotopy groups
The stable homotopy groups πk are the product of cyclic groups of the infinite or prime power ordersshown in the table. (For largely historical reasons, stable homotopy groups are usually given as products of cyclic groups of prime power order, while tables of unstable homotopy groups often give them as products of the smallest number of cyclic groups.) The main complexity is in the 2-, 3-, and 5-components: for p > 5, the p-components in the range of the table are accounted for by the J-homomorphism and are cyclic of order p if 2(p−1) divides k+1 and 0 otherwise . (The 2-components can be found in , though there were some errors for k≥54 that were corrected by , and the 3- and 5-components in .) The mod 8 behavior of the table comes from Bott periodicity via the J-homomorphism
J-homomorphism
In mathematics, the J-homomorphism is a mapping from the homotopy groups of the special orthogonal groups to the homotopy groups of spheres. It was defined by , extending a construction of .-Definition:...
, whose image is underlined.
| n → | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| π0+nS | ∞ | 2 | 2 | 8⋅3 | ⋅ | ⋅ | 2 | 16⋅3⋅5 |
| π8+nS | 2⋅2 | 2⋅22 | 2⋅3 | 8⋅9⋅7 | ⋅ | 3 | 22 | 32⋅2⋅3⋅5 |
| π16+nS | 2⋅2 | 2⋅23 | 8⋅2 | 8⋅2⋅3⋅11 | 8⋅3 | 22 | 2⋅2 | 16⋅8⋅2⋅9⋅3⋅5⋅7⋅13 |
| π24+nS | 2⋅2 | 2⋅2 | 22⋅3 | 8⋅3 | 2 | 3 | 2⋅3 | 64⋅22⋅3⋅5⋅17 |
| π32+nS | 2⋅23 | 2⋅24 | 4⋅23 | 8⋅22⋅27⋅7⋅19 | 2⋅3 | 22⋅3 | 4⋅2⋅3⋅5 | 16⋅25⋅3⋅3⋅25⋅11 |
| π40+nS | 2⋅4⋅24⋅3 | 2⋅24 | 8⋅22⋅3 | 8⋅3⋅23 | 8 | 16⋅23⋅9⋅5 | 24⋅3 | 32⋅4⋅23⋅9⋅3⋅5⋅7⋅13 |
| π48+nS | 2⋅4⋅23 | 2⋅2⋅3 | 23⋅3 | 8⋅4⋅22⋅3 | 23⋅3 | 24 | 4⋅2 | 16⋅3⋅3⋅5⋅29 |
| π56+nS | 2⋅2 | 2⋅23 | 22 | 8⋅22⋅9⋅7⋅11⋅31 | 4 | ⋅ | 4⋅22⋅3 | 128⋅23⋅3⋅5⋅17 |
External links
in MacTutor History of Mathematics archiveMacTutor History of Mathematics archive
The MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland...
. in MacTutor History of Mathematics archive.

