
Pushforward (homology)
Encyclopedia
In algebraic topology
, the pushforward of a continuous function
 :
: 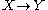 between two topological space
between two topological space
s is a homomorphism
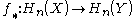 between the homology groups for
between the homology groups for 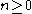 .
.
Homology is a functor
which converts a topological space into a sequence of homology groups
into a sequence of homology groups  . (Often, the collection of all such groups is referred to using the notation
. (Often, the collection of all such groups is referred to using the notation 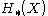 ; this collection has the structure of a graded group.) In any category
; this collection has the structure of a graded group.) In any category
, a functor must induce a corresponding morphism
. The pushforward is the morphism corresponding to the homology functor.
First we have an induced homomorphism between the singular or simplicial chain complex
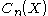 and
and  defined by composing each singular n-simplex
defined by composing each singular n-simplex
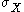 :
: 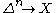 with
with 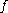 to obtain a singular n-simplex of
to obtain a singular n-simplex of 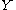 ,
, 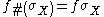 :
:  . Then we extend
. Then we extend 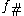 linearly via
linearly via 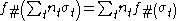 .
.
The maps :
: 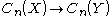 satisfy
satisfy 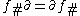 where
where 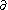 is the boundary operator between chain groups, so
is the boundary operator between chain groups, so 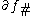 defines a chain map.
defines a chain map.
We have that takes cycles to cycles, since
takes cycles to cycles, since 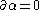 implies
implies 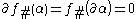 . Also
. Also  takes boundaries to boundaries since
takes boundaries to boundaries since 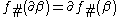 .
.
Hence induces a homomorphism between the homology groups
induces a homomorphism between the homology groups 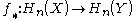 for
for 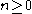 .
.
A main result about the push-forward is the homotopy invariance: if two maps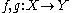 are homotopic, then they induce the same homomorphism
are homotopic, then they induce the same homomorphism 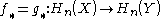 .
.
This immediately implies that the homology groups of homotopy equivalent spaces are isomorphic:
The maps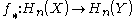 induced by a homotopy equivalence
induced by a homotopy equivalence 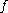 :
: 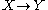 are isomorphisms for all
are isomorphisms for all  .
.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the pushforward of a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
 :
: 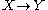 between two topological space
between two topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
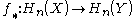 between the homology groups for
between the homology groups for 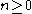 .
.Homology is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
which converts a topological space
 into a sequence of homology groups
into a sequence of homology groups  . (Often, the collection of all such groups is referred to using the notation
. (Often, the collection of all such groups is referred to using the notation 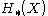 ; this collection has the structure of a graded group.) In any category
; this collection has the structure of a graded group.) In any categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, a functor must induce a corresponding morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
. The pushforward is the morphism corresponding to the homology functor.
Definition for singular and simplicial homology
We build the pushforward homomorphism as follows (for singular or simplicial homology):First we have an induced homomorphism between the singular or simplicial chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
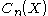 and
and  defined by composing each singular n-simplex
defined by composing each singular n-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
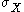 :
: 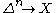 with
with 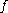 to obtain a singular n-simplex of
to obtain a singular n-simplex of 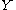 ,
, 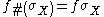 :
:  . Then we extend
. Then we extend 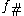 linearly via
linearly via 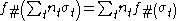 .
.The maps
 :
: 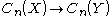 satisfy
satisfy 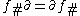 where
where 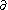 is the boundary operator between chain groups, so
is the boundary operator between chain groups, so 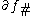 defines a chain map.
defines a chain map.We have that
 takes cycles to cycles, since
takes cycles to cycles, since 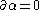 implies
implies 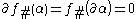 . Also
. Also  takes boundaries to boundaries since
takes boundaries to boundaries since 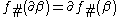 .
.Hence
 induces a homomorphism between the homology groups
induces a homomorphism between the homology groups 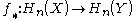 for
for 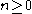 .
.Properties and homotopy invariance
Two basic properties of the push-forward are:-
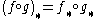 for the composition of maps
for the composition of maps 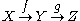 .
. -
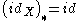 where
where 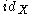 :
:  refers to identity function of
refers to identity function of  and
and  refers to the identity isomorphism of homology groups.
refers to the identity isomorphism of homology groups.
A main result about the push-forward is the homotopy invariance: if two maps
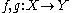 are homotopic, then they induce the same homomorphism
are homotopic, then they induce the same homomorphism 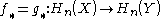 .
.This immediately implies that the homology groups of homotopy equivalent spaces are isomorphic:
The maps
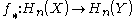 induced by a homotopy equivalence
induced by a homotopy equivalence 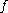 :
: 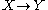 are isomorphisms for all
are isomorphisms for all  .
.

