Duality (mathematics)
Encyclopedia
In mathematics
, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often (but not always) by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have fixed points
, the dual of A is sometimes A itself. For example, Desargues' theorem
in projective geometry
is self-dual in this sense.
In mathematical contexts, duality has numerous meanings, and although it is “a very pervasive and important concept in (modern) mathematics” and “an important general theme that has manifestations in almost every area of mathematics”, there is no single universally agreed definition that unifies all concepts of duality.
Many mathematical dualities between objects of two types correspond to pairing
s, bilinear functions from an object of one type and another object of the second type to some family of scalars. For instance, linear algebra duality corresponds in this way to bilinear maps from pairs of vector spaces to scalars, the duality between distributions
and the associated test functions corresponds to the pairing in which one integrates a distribution against a test function, and Poincaré duality
corresponds similarly to intersection number
, viewed as a pairing between submanifolds of a given manifold.
. The dual
of a poset P = (X, ≤) is the poset Pd = (X, ≥) comprising the same ground set but the converse relation. Familiar examples of dual partial orders include
A concept defined for a partial order P will correspond to a dual concept on the dual poset Pd. For instance, a minimal element of P will be a maximal element
of Pd: minimality and maximality are dual concepts in order theory. Other pairs of dual concepts are upper and lower bounds, lower sets and upper set
s, and ideals
and filters
.
A particular order reversal of this type occurs in the family of all subsets of some set S: if
denotes the complement set, then 
if and only if 
. In topology, open set
s and closed set
s are dual concepts: the complement of an open set is closed, and vice versa. In matroid
theory, the family of sets complementary to the independent sets of a given matroid themselves form another matroid, called the dual matroid. In logic
, one may represent a truth assignment to the variables of an unquantified formula as a set, the variables that are true for the assignment. A truth assignment satisfies the formula if and only if the complementary truth assignment satisfies the De Morgan dual of its formula. The existential and universal quantifiers in logic are similarly dual.
A partial order may be interpreted as a category
in which there is an arrow from x to y in the category if and only if x ≤ y in the partial order. The order-reversing duality of partial orders can be extended to the concept of a dual category, the category formed by reversing all the arrows in a given category. Many of the specific dualities described later are dualities of categories in this sense.
According to Artstein-Avidan and Milman, a duality transform is just an involutive antiautomorphism
of a partially ordered set
S, that is, an order-reversing involution
Surprisingly, in several important cases these simple properties determine the transform uniquely up to some simple symmetries. If 
are two duality transforms then their composition
is an order automorphism
of S; thus, any two duality transforms differ only by an order automorphism. For example, all order automorphisms of a power set S = 2R are induced by permutations of R. The papers cited above treat only sets S of functions on Rn satisfying some condition of convexity and prove that all order automorphisms are induced by linear or affine transformations of Rn.
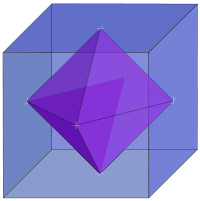There are many distinct but interrelated dualities in which geometric or topological objects correspond to other objects of the same type, but with a reversal of the dimensions of the features of the objects. A classical example of this is the duality of the platonic solid
s, in which the cube and the octahedron form a dual pair, the dodecahedron and the icosahedron form a dual pair, and the tetrahedron is self-dual. The dual polyhedron
of any of these polyhedra may be formed as the convex hull
of the center points of each face of the primal polyhedron, so the vertices
of the dual correspond one-for-one with the faces of the primal. Similarly, each edge of the dual corresponds to an edge of the primal, and each face of the dual corresponds to a vertex of the primal. These correspondences are incidence-preserving: if two parts of the primal polyhedron touch each other, so do the corresponding two parts of the dual polyhedron
. More generally, using the concept of polar reciprocation
, any convex polyhedron, or more generally any convex polytope
, corresponds to a dual polyhedron
or dual polytope, with an i-dimensional feature of an n-dimensional polytope corresponding to an (n − i − 1)-dimensional feature of the dual polytope. The incidence-preserving nature of the duality is reflected in the fact that the face lattices of the primal and dual polyhedra or polytopes are themselves order-theoretic duals. Duality of polytopes and order-theoretic duality are both involutions: the dual polytope of the dual polytope of any polytope is the original polytope, and reversing all order-relations twice returns to the original order. Choosing a different center of polarity leads to geometrically different dual polytopes, but all have the same combinatorial structure.
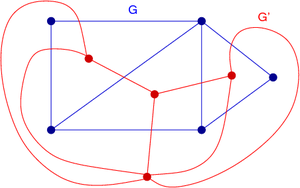From any three-dimensional polyhedron, one can form a planar graph
, the graph of its vertices and edges. The dual polyhedron has a dual graph
, a graph with one vertex for each face of the polyhedron and with one edge for every two adjacent faces. The same concept of planar graph duality may be generalized to graphs that are drawn in the plane but that do not come from a three-dimensional polyhedron, or more generally to graph embedding
s on surfaces of higher genus: one may draw a dual graph by placing one vertex within each region bounded by a cycle of edges in the embedding, and drawing an edge connecting any two regions that share a boundary edge. An important example of this type comes from computational geometry
: the duality for any finite set S of points in the plane between the Delaunay triangulation
of S and the Voronoi diagram
of S. As with dual polyhedra and dual polytopes, the duality of graphs on surfaces is a dimension-reversing involution: each vertex in the primal embedded graph corresponds to a region of the dual embedding, each edge in the primal is crossed by an edge in the dual, and each region of the primal corresponds to a vertex of the dual. The dual graph depends on how the primal graph is embedded: different planar embeddings of a single graph may lead to different dual graphs. Matroid duality is an algebraic extension of planar graph duality, in the sense that the dual matroid of the graphic matroid of a planar graph is isomorphic to the graphic matroid of the dual graph.
In topology, Poincaré duality
also reverses dimensions; it corresponds to the fact that, if a topological manifold
is respresented as a cell complex, then the dual of the complex (a higher dimensional generalization of the planar graph dual) represents the same manifold. In Poincaré duality, this homeomorphism is reflected in an isomorphism of the kth homology
group and the (n − k)th cohomology
group.
Another example of a dimension-reversing duality arises in projective geometry
. In the projective plane
, it is possible to find geometric transformations that map each point of the projective plane to a line, and each line of the projective plane to a point, in an incidence-preserving way: in terms of the incidence matrix
of the points and lines in the plane, this operation is just that of forming the transpose
. Transformations of this type exist also in any higher dimension; one way to construct them is to use the same polar transformations
that generate polyhedron and polytope duality. Due to this ability to replace any configuration of points and lines with a corresponding configuration of lines and points, there arises a general principle of duality in projective geometry
: given any theorem in plane projective geometry, exchanging the terms "point" and "line" everywhere results in a new, equally valid theorem.
The points, lines, and higher dimensional subspaces n-dimensional projective space may be interpreted as describing the linear subspaces of an (n + 1)-dimensional vector space
; if this vector space is supplied with an inner product the transformation from any linear subspace to its perpendicular subspace is an example of a projective duality. The Hodge dual
extends this duality within an inner product space by providing a canonical correspondence between the elements of the exterior algebra
.
A kind of geometric duality also occurs in optimization theory
, but not one that reverses dimensions. A linear program may be specified by a system of real variables (the coordinates for a point in Euclidean space Rn), a system of linear constraints (specifying that the point lie in a halfspace; the intersection of these halfspaces is a convex polytope, the feasible region of the program), and a linear function (what to optimize). Every linear program has a dual problem
with the same optimal solution, but the variables in the dual problem correspond to constraints in the primal problem and vice versa.
Other analogous dualities follow from these:
Topology
inherits a duality between open
and closed subset
s of some fixed topological space X: a subset U of X is closed if and only if its complement in X is open. Because of this, many theorems about closed sets are dual to theorems about open sets. For example, any union of open sets is open, so dually, any intersection of closed sets is closed. The interior
of a set is the largest open set contained in it, and the closure
of the set is the smallest closed set that contains it. Because of the duality, the complement of the interior of any set U is equal to the closure of the complement of U.
The collection of all open subsets of a topological space X forms a complete Heyting algebra
. There is a duality, known as Stone duality
, connecting sober space
s and spatial locales.
V is defined as
The set of morphisms, i.e., linear maps, is a vector space in its own right. There is always a natural, injective map V → V∗∗ given by v ↦ (f ↦ f(v)), where f is an element of the dual space. That map is an isomorphism if and only if the dimension of V is finite.
In the realm of topological vector space
s, a similar construction exists, replacing the dual by the topological dual vector space. A topological vector space that is canonically isomorphic to its bidual is called reflexive space
.
The dual lattice of a lattice
L is given by
which is used in the construction of toric varieties. The Pontryagin dual of locally compact topological group
s G is given by
continuous group homomorphisms with values in the circle (with multiplication of complex numbers as group operation).
, this amounts to a contravariant functor between two categories
C and D:
which for any two objects X and Y of C gives a map
That functor may or may not be an equivalence of categories
. There are various situations, where such a functor is an equivalence between the opposite category
Cop of C, and D. Using a duality of this type, every statement in the first theory can be translated into a "dual" statement in the second theory, where the direction of all arrows has to be reversed. Therefore, any duality between categories C and D is formally the same as an equivalence between C and Dop (Cop and D). However, in many circumstances the opposite categories have no inherent meaning, which makes duality an additional, separate concept.
Many category-theoretic
notions come in pairs in the sense that they correspond to each other while considering the opposite category. For example, Cartesian product
s Y1 × Y2 and disjoint union
s Y1 ⊔ Y2 of sets are dual to each other in the sense that
and
for any set X. This is a particular case of a more general duality phenomenon, under which limits
in a category C correspond to colimits in the opposite category Cop; further concrete examples of this are epimorphism
s vs. monomorphism
, in particular factor modules (or groups etc.) vs. submodules, direct product
s vs. direct sums (also called coproduct
s to emphasize the duality aspect). Therefore, in some cases, proofs of certain statements can be halved, using such a duality phenomenon. Further notions displaying related by such a categorical duality are projective
and injective module
s in homological algebra
, fibration
s and cofibration
s in topology and more generally model categories
.
Two functors F: C → D and G: D → C are adjoint if for all objects c in C and d in D
in a natural way. Actually, the correspondence of limits and colimits is an example of adjoints, since there is an adjunction
between the colimit functor that assigns to any diagram in C indexed by some category I its colimit and the diagonal functor that maps any object c of C to the constant diagramm which has c at all places. Dually,
s and affine schemes: to every commutative ring A there is an affine spectrum, Spec A
, conversely, given an affine scheme S, one gets back a ring by taking global sections of the structure sheaf OS. In addition, ring homomorphism
s are in one-to-one correspondence with morphisms of affine schemes, thereby there is an equivalenceop ≅ (affine schemes)
Compare with noncommutative geometry
and Gelfand duality.
In a number of situations, the objects of two categories linked by a duality are partially ordered, i.e., there is some notion of an object "being smaller" than another one. In such a situation, a duality that respects the orderings in question is known as a Galois connection
. An example is the standard duality in Galois theory
(fundamental theorem of Galois theory
) between field extension
s and subgroup
s of the Galois group
: a bigger field extension corresponds—under the mapping that assigns to any extension L ⊃ K (inside some fixed bigger field Ω) the Galois group Gal(Ω / L)—to a smaller group.
Pontryagin duality
gives a duality on the category of locally compact abelian group
s: given any such group G, the character group
given by continuous group homomorphisms from G to the circle group S1 can be endowed with the compact-open topology
. Pontryagin duality states that the character group is again locally compact abelian and that
Moreover, discrete group
s correspond to compact abelian group
s; finite groups correspond to finite groups. Pontryagin is the background to Fourier analysis, see below.
Both Gelfand and Pontryagin duality can be deduced in a largely formal, category-theoretic way.
, problems are frequently solved by passing to the dual description of functions and operators.
Fourier transform
switches between functions on a vector space and its dual:
and conversely
If f is an L2-function
on R or RN, say, then so is
and 
. Moreover, the transform interchanges operations of multiplication and convolution
on the corresponding function space
s. A conceptual explanation of the Fourier transform is obtained by the aforementioned Pontryagin duality, applied to the locally compact groups R (or RN etc.): any character of R is given by
. The dualizing character of Fourier transform has many other manifestations, for example, in alternative descriptions of quantum mechanical
systems in terms of coordinate and momentum representations.
s (in the sense of linear algebra) of other objects of interest are often called dualities. Many of these dualities are given by a bilinear pairing of two K-vector spaces
For perfect pairings, there is, therefore, an isomorphism of A to the dual of B.
For example, Poincaré duality
of a smooth compact complex manifold
X is given by a pairing of singular cohomology with C-coefficients (equivalently, sheaf cohomology
of the constant sheaf
C)
where n is the (complex) dimension of X. Poincaré duality can also be expressed as a relation of singular homology
and de Rham cohomology
, by asserting that the map
(integrating a differential k-form over an 2n−k-(real)-dimensional cycle) is a perfect pairing.
The same duality pattern holds for a smooth projective variety over a separably closed field, using l-adic cohomology with Qℓ-coefficients instead. This is further generalized to possibly singular varieties, using intersection cohomology
instead, a duality called Verdier duality
. With increasing level of generality, it turns out, an increasing amount of technical background is helpful or necessary to understand these theorems: the modern formulation of both these dualities can be done using derived categories
and certain direct and inverse image functors of sheaves
, applied to locally constant sheaves (with respect to the classical analytical topology in the first case, and with respect to the étale topology
in the second case).
Yet another group of similar duality statements is encountered in arithmetics: étale cohomology of finite
, local
and global field
s (also known as Galois cohomology
, since étale cohomology over a field is equivalent to group cohomology
of the (absolute) Galois group
of the field) admit similar pairings. The absolute Galois group G(Fq) of a finite field, for example, is isomorphic to
, the profinite completion of Z, the integers. Therefore, the perfect pairing (for any G-module
M)
is a direct consequence of Pontryagin duality
of finite groups. For local and global fields, similar statements exist (local duality and global or Poitou–Tate duality).
Serre duality
or coherent duality
are similar to the statements above, but applies to cohomology of coherent sheaves instead.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often (but not always) by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, the dual of A is sometimes A itself. For example, Desargues' theorem
Desargues' theorem
In projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
in projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
is self-dual in this sense.
In mathematical contexts, duality has numerous meanings, and although it is “a very pervasive and important concept in (modern) mathematics” and “an important general theme that has manifestations in almost every area of mathematics”, there is no single universally agreed definition that unifies all concepts of duality.
Many mathematical dualities between objects of two types correspond to pairing
Pairing
The concept of pairing treated here occurs in mathematics.-Definition:Let R be a commutative ring with unity, and let M, N and L be three R-modules.A pairing is any R-bilinear map e:M \times N \to L...
s, bilinear functions from an object of one type and another object of the second type to some family of scalars. For instance, linear algebra duality corresponds in this way to bilinear maps from pairs of vector spaces to scalars, the duality between distributions
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
and the associated test functions corresponds to the pairing in which one integrates a distribution against a test function, and Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
corresponds similarly to intersection number
Intersection number
In mathematics, and especially in algebraic geometry, the intersection number generalizes the intuitive notion of counting the number of times two curves intersect to higher dimensions, multiple curves, and accounting properly for tangency...
, viewed as a pairing between submanifolds of a given manifold.
Order-reversing dualities
A particularly simple form of duality comes from order theoryOrder theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
. The dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
of a poset P = (X, ≤) is the poset Pd = (X, ≥) comprising the same ground set but the converse relation. Familiar examples of dual partial orders include
- the subset and superset relations
and 
on any collection of sets,
- the divides and multiple-of relations on the integers, and
- the descendant-of and ancestor-of relations on the set of humans.
A concept defined for a partial order P will correspond to a dual concept on the dual poset Pd. For instance, a minimal element of P will be a maximal element
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
of Pd: minimality and maximality are dual concepts in order theory. Other pairs of dual concepts are upper and lower bounds, lower sets and upper set
Upper set
In mathematics, an upper set of a partially ordered set is a subset U with the property that x is in U and x≤y imply y is in U....
s, and ideals
Ideal (order theory)
In mathematical order theory, an ideal is a special subset of a partially ordered set . Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion...
and filters
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
.
A particular order reversal of this type occurs in the family of all subsets of some set S: if
denotes the complement set, then if and only if . In topology, open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s and closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s are dual concepts: the complement of an open set is closed, and vice versa. In matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
theory, the family of sets complementary to the independent sets of a given matroid themselves form another matroid, called the dual matroid. In logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, one may represent a truth assignment to the variables of an unquantified formula as a set, the variables that are true for the assignment. A truth assignment satisfies the formula if and only if the complementary truth assignment satisfies the De Morgan dual of its formula. The existential and universal quantifiers in logic are similarly dual.
A partial order may be interpreted as a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
in which there is an arrow from x to y in the category if and only if x ≤ y in the partial order. The order-reversing duality of partial orders can be extended to the concept of a dual category, the category formed by reversing all the arrows in a given category. Many of the specific dualities described later are dualities of categories in this sense.
According to Artstein-Avidan and Milman, a duality transform is just an involutive antiautomorphism
of a partially ordered setPartially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
S, that is, an order-reversing involution
Surprisingly, in several important cases these simple properties determine the transform uniquely up to some simple symmetries. If are two duality transforms then their compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
is an order automorphism
Order isomorphism
In the mathematical field of order theory an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets . Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that one of...
of S; thus, any two duality transforms differ only by an order automorphism. For example, all order automorphisms of a power set S = 2R are induced by permutations of R. The papers cited above treat only sets S of functions on Rn satisfying some condition of convexity and prove that all order automorphisms are induced by linear or affine transformations of Rn.
Dimension-reversing dualities
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, in which the cube and the octahedron form a dual pair, the dodecahedron and the icosahedron form a dual pair, and the tetrahedron is self-dual. The dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of any of these polyhedra may be formed as the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the center points of each face of the primal polyhedron, so the vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of the dual correspond one-for-one with the faces of the primal. Similarly, each edge of the dual corresponds to an edge of the primal, and each face of the dual corresponds to a vertex of the primal. These correspondences are incidence-preserving: if two parts of the primal polyhedron touch each other, so do the corresponding two parts of the dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
. More generally, using the concept of polar reciprocation
Pole and polar
In geometry, the terms pole and polar are used to describe a point and a line that have a unique reciprocal relationship with respect to a given conic section...
, any convex polyhedron, or more generally any convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
, corresponds to a dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
or dual polytope, with an i-dimensional feature of an n-dimensional polytope corresponding to an (n − i − 1)-dimensional feature of the dual polytope. The incidence-preserving nature of the duality is reflected in the fact that the face lattices of the primal and dual polyhedra or polytopes are themselves order-theoretic duals. Duality of polytopes and order-theoretic duality are both involutions: the dual polytope of the dual polytope of any polytope is the original polytope, and reversing all order-relations twice returns to the original order. Choosing a different center of polarity leads to geometrically different dual polytopes, but all have the same combinatorial structure.
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
, the graph of its vertices and edges. The dual polyhedron has a dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
, a graph with one vertex for each face of the polyhedron and with one edge for every two adjacent faces. The same concept of planar graph duality may be generalized to graphs that are drawn in the plane but that do not come from a three-dimensional polyhedron, or more generally to graph embedding
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
s on surfaces of higher genus: one may draw a dual graph by placing one vertex within each region bounded by a cycle of edges in the embedding, and drawing an edge connecting any two regions that share a boundary edge. An important example of this type comes from computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
: the duality for any finite set S of points in the plane between the Delaunay triangulation
Delaunay triangulation
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
of S and the Voronoi diagram
Voronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
of S. As with dual polyhedra and dual polytopes, the duality of graphs on surfaces is a dimension-reversing involution: each vertex in the primal embedded graph corresponds to a region of the dual embedding, each edge in the primal is crossed by an edge in the dual, and each region of the primal corresponds to a vertex of the dual. The dual graph depends on how the primal graph is embedded: different planar embeddings of a single graph may lead to different dual graphs. Matroid duality is an algebraic extension of planar graph duality, in the sense that the dual matroid of the graphic matroid of a planar graph is isomorphic to the graphic matroid of the dual graph.
In topology, Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
also reverses dimensions; it corresponds to the fact that, if a topological manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is respresented as a cell complex, then the dual of the complex (a higher dimensional generalization of the planar graph dual) represents the same manifold. In Poincaré duality, this homeomorphism is reflected in an isomorphism of the kth homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
group and the (n − k)th cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
group.
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
. In the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
, it is possible to find geometric transformations that map each point of the projective plane to a line, and each line of the projective plane to a point, in an incidence-preserving way: in terms of the incidence matrix
Incidence matrix
In mathematics, an incidence matrix is a matrix that shows the relationship between two classes of objects. If the first class is X and the second is Y, the matrix has one row for each element of X and one column for each element of Y. The entry in row x and column y is 1 if x and y are related ...
of the points and lines in the plane, this operation is just that of forming the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
. Transformations of this type exist also in any higher dimension; one way to construct them is to use the same polar transformations
Pole and polar
In geometry, the terms pole and polar are used to describe a point and a line that have a unique reciprocal relationship with respect to a given conic section...
that generate polyhedron and polytope duality. Due to this ability to replace any configuration of points and lines with a corresponding configuration of lines and points, there arises a general principle of duality in projective geometry
Duality (projective geometry)
A striking feature of projective planes is the "symmetry" of the roles played by points and lines in the definitions and theorems, and duality is the formalization of this metamathematical concept. There are two approaches to the subject of duality, one through language and the other a more...
: given any theorem in plane projective geometry, exchanging the terms "point" and "line" everywhere results in a new, equally valid theorem.
The points, lines, and higher dimensional subspaces n-dimensional projective space may be interpreted as describing the linear subspaces of an (n + 1)-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
; if this vector space is supplied with an inner product the transformation from any linear subspace to its perpendicular subspace is an example of a projective duality. The Hodge dual
Hodge dual
In mathematics, the Hodge star operator or Hodge dual is a significant linear map introduced in general by W. V. D. Hodge. It is defined on the exterior algebra of a finite-dimensional oriented inner product space.-Dimensions and algebra:...
extends this duality within an inner product space by providing a canonical correspondence between the elements of the exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
.
A kind of geometric duality also occurs in optimization theory
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, but not one that reverses dimensions. A linear program may be specified by a system of real variables (the coordinates for a point in Euclidean space Rn), a system of linear constraints (specifying that the point lie in a halfspace; the intersection of these halfspaces is a convex polytope, the feasible region of the program), and a linear function (what to optimize). Every linear program has a dual problem
Dual problem
In constrained optimization, it is often possible to convert the primal problem to a dual form, which is termed a dual problem. Usually dual problem refers to the Lagrangian dual problem but other dual problems are used, for example, the Wolfe dual problem and the Fenchel dual problem...
with the same optimal solution, but the variables in the dual problem correspond to constraints in the primal problem and vice versa.
Duality in logic and set theory
In logic, functions or relations A and B are considered dual if A(¬x) = ¬B(x), where ¬ is logical negation. The basic duality of this type is the duality of the ∃ and ∀ quantifiers. These are dual because ∃x.¬P(x) and ¬∀x.P(x) are equivalent for all predicates P: if there exists an x for which P fails to hold, then it is false that P holds for all x. From this fundamental logical duality follow several others:- A formula is said to be satisfiable in a certain model if there are assignments to its free variables that render it true; it is valid if every assignment to its free variables makes it true. Satisfiability and validity are dual because the invalid formulas are precisely those whose negations are satisfiable, and the unsatisfiable formulas are those whose negations are valid. This can be viewed as a special case of the previous item, with the quantifiers ranging over interpretations.
- In classical logic, the ∧ and ∨ operators are dual in this sense, because (¬x ∧ ¬y) and ¬(x ∨ y) are equivalent. This means that for every theorem of classical logic there is an equivalent dual theorem. De Morgan's laws are examples. More generally,
. The left side is true if and only if ∀i.¬xi, and the right side if and only if ¬∃i.xi.
- In modal logicModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
,
means that the proposition p is "necessarily" true, and 
that p is "possibly" true. Most interpretations of modal logic assign dual meanings to these two operators. For example in Kripke semanticsKripke semanticsKripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
, "p is possibly true" means "there exists some world W in which p is true", while "p is necessarily true" means "for all worlds W, p is true". The duality of
and 
then follows from the analogous duality of ∀ and ∃. Other dual modal operators behave similarly. For example, temporal logicTemporal logicIn logic, the term temporal logic is used to describe any system of rules and symbolism for representing, and reasoning about, propositions qualified in terms of time. In a temporal logic we can then express statements like "I am always hungry", "I will eventually be hungry", or "I will be hungry...
has operators denoting "will be true at some time in the future" and "will be true at all times in the future" which are similarly dual.
Other analogous dualities follow from these:
- Set-theoretic union and intersection are dual under the set complement operator C. That is,
, and more generally, 
. This follows from the duality of ∀ and ∃: an element x is a member of 
if and only if ∀α.¬x∈Aα, and is a member of 
if and only if ¬∃α.x∈Aα.
Topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
inherits a duality between open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
and closed subset
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s of some fixed topological space X: a subset U of X is closed if and only if its complement in X is open. Because of this, many theorems about closed sets are dual to theorems about open sets. For example, any union of open sets is open, so dually, any intersection of closed sets is closed. The interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of a set is the largest open set contained in it, and the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the set is the smallest closed set that contains it. Because of the duality, the complement of the interior of any set U is equal to the closure of the complement of U.
The collection of all open subsets of a topological space X forms a complete Heyting algebra
Heyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
. There is a duality, known as Stone duality
Stone duality
In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation...
, connecting sober space
Sober space
In mathematics, a sober space is a topological spacesuch that every irreducible closed subset of X is the closure of exactly one point of X: that is, has a unique generic point.-Properties and examples :...
s and spatial locales.
- Birkhoff's representation theoremBirkhoff's representation theoremIn mathematics, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice can be represented as finite sets, in such a way that the lattice operations correspond to unions and intersections of sets...
relating distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
s and partial orders
Dual objects
A group of dualities can be described by endowing, for any mathematical object X, the set of morphisms Hom(X, D) into some fixed object D, with a structure similar to the one of X. This is sometimes called internal Hom. In general, this yields a true duality only for specific choices of D, in which case X∗=Hom(X, D) is referred to as the dual of X. It may or may not be true that the bidual, that is to say, the dual of the dual, X∗∗ = (X∗)∗ is isomorphic to X, as the following example, which is underlying many other dualities, shows: the dual vector space V∗ of a K-vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V is defined as
- V∗ = Hom (V, K).
The set of morphisms, i.e., linear maps, is a vector space in its own right. There is always a natural, injective map V → V∗∗ given by v ↦ (f ↦ f(v)), where f is an element of the dual space. That map is an isomorphism if and only if the dimension of V is finite.
In the realm of topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, a similar construction exists, replacing the dual by the topological dual vector space. A topological vector space that is canonically isomorphic to its bidual is called reflexive space
Reflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
.
The dual lattice of a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
L is given by
- Hom(L, Z),
which is used in the construction of toric varieties. The Pontryagin dual of locally compact topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s G is given by
- Hom(G, S1),
continuous group homomorphisms with values in the circle (with multiplication of complex numbers as group operation).
Opposite category and adjoint functors
In another group of dualities, the objects of one theory are translated into objects of another theory and the maps between objects in the first theory are translated into morphisms in the second theory, but with direction reversed. Using the parlance of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, this amounts to a contravariant functor between two categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C and D:
- F: C → D
which for any two objects X and Y of C gives a map
- HomC(X, Y) → HomD(F(Y), F(X))
That functor may or may not be an equivalence of categories
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
. There are various situations, where such a functor is an equivalence between the opposite category
Opposite category
In category theory, a branch of mathematics, the opposite category or dual category Cop of a given category C is formed by reversing the morphisms, i.e. interchanging the source and target of each morphism. Doing the reversal twice yields the original category, so the opposite of an opposite...
Cop of C, and D. Using a duality of this type, every statement in the first theory can be translated into a "dual" statement in the second theory, where the direction of all arrows has to be reversed. Therefore, any duality between categories C and D is formally the same as an equivalence between C and Dop (Cop and D). However, in many circumstances the opposite categories have no inherent meaning, which makes duality an additional, separate concept.
Many category-theoretic
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
notions come in pairs in the sense that they correspond to each other while considering the opposite category. For example, Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s Y1 × Y2 and disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
s Y1 ⊔ Y2 of sets are dual to each other in the sense that
- Hom(X, Y1 × Y2) = Hom(X, Y1) × Hom(X, Y2)
and
- Hom(Y1 ⊔ Y2, X) = Hom(Y1, X) × Hom(Y2, X)
for any set X. This is a particular case of a more general duality phenomenon, under which limits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
in a category C correspond to colimits in the opposite category Cop; further concrete examples of this are epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
s vs. monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, in particular factor modules (or groups etc.) vs. submodules, direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
s vs. direct sums (also called coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s to emphasize the duality aspect). Therefore, in some cases, proofs of certain statements can be halved, using such a duality phenomenon. Further notions displaying related by such a categorical duality are projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
and injective module
Injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
s in homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, fibration
Fibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
s and cofibration
Cofibration
In mathematics, in particular homotopy theory, a continuous mappingi\colon A \to X,where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines...
s in topology and more generally model categories
Model category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
.
Two functors F: C → D and G: D → C are adjoint if for all objects c in C and d in D
- HomD(F(c), d) ≅ HomC(c, G(d)),
in a natural way. Actually, the correspondence of limits and colimits is an example of adjoints, since there is an adjunction
between the colimit functor that assigns to any diagram in C indexed by some category I its colimit and the diagonal functor that maps any object c of C to the constant diagramm which has c at all places. Dually,
Examples
For example, there is a duality between commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s and affine schemes: to every commutative ring A there is an affine spectrum, Spec A
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
, conversely, given an affine scheme S, one gets back a ring by taking global sections of the structure sheaf OS. In addition, ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
s are in one-to-one correspondence with morphisms of affine schemes, thereby there is an equivalenceop ≅ (affine schemes)
Compare with noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
and Gelfand duality.
In a number of situations, the objects of two categories linked by a duality are partially ordered, i.e., there is some notion of an object "being smaller" than another one. In such a situation, a duality that respects the orderings in question is known as a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
. An example is the standard duality in Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
(fundamental theorem of Galois theory
Fundamental theorem of Galois theory
In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...
) between field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s and subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
: a bigger field extension corresponds—under the mapping that assigns to any extension L ⊃ K (inside some fixed bigger field Ω) the Galois group Gal(Ω / L)—to a smaller group.
Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
gives a duality on the category of locally compact abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s: given any such group G, the character group
Character group
In mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory...
- χ(G) = Hom(G, S1)
given by continuous group homomorphisms from G to the circle group S1 can be endowed with the compact-open topology
Compact-open topology
In mathematics, the compact-open topology is a topology defined on the set of continuous maps between two topological spaces. The compact-open topology is one of the commonly-used topologies on function spaces, and is applied in homotopy theory and functional analysis...
. Pontryagin duality states that the character group is again locally compact abelian and that
- G ≅ χ(χ(G)).
Moreover, discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
s correspond to compact abelian group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
s; finite groups correspond to finite groups. Pontryagin is the background to Fourier analysis, see below.
- Tannaka-Krein dualityTannaka-Krein dualityIn mathematics, Tannaka–Krein duality theory concerns the interaction of a compact topological group and its category of linear representations. Its natural extension to the non-Abelian case is the Grothendieck duality theory....
, a non-commutative analogue of Pontryagin duality - Gelfand duality relating commutative C*-algebras and compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s
Both Gelfand and Pontryagin duality can be deduced in a largely formal, category-theoretic way.
Analytic dualities
In analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, problems are frequently solved by passing to the dual description of functions and operators.
Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
switches between functions on a vector space and its dual:
and conversely
If f is an L2-function
Lebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
on R or RN, say, then so is
and . Moreover, the transform interchanges operations of multiplication and convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
on the corresponding function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s. A conceptual explanation of the Fourier transform is obtained by the aforementioned Pontryagin duality, applied to the locally compact groups R (or RN etc.): any character of R is given by
. The dualizing character of Fourier transform has many other manifestations, for example, in alternative descriptions of quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
systems in terms of coordinate and momentum representations.
- Laplace transform is similar to Fourier transform and interchanges operators of multiplication by polynomials with constant coefficient linear differential operators.
- Legendre transformationLegendre transformationIn mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
is an important analytic duality which switches between velocitiesVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
in Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
and momentaMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
in Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
.
Poincaré-style dualities
Theorems showing that certain objects of interest are the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
s (in the sense of linear algebra) of other objects of interest are often called dualities. Many of these dualities are given by a bilinear pairing of two K-vector spaces
- A ⊗ B → K.
For perfect pairings, there is, therefore, an isomorphism of A to the dual of B.
For example, Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
of a smooth compact complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
X is given by a pairing of singular cohomology with C-coefficients (equivalently, sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
of the constant sheaf
Constant sheaf
In mathematics, the constant sheaf on a topological space X associated to a set A is a sheaf of sets on X whose stalks are all equal to A. It is denoted by or AX. The constant presheaf with value A is the presheaf that assigns to each open subset of X the value A, and all of whose restriction maps...
C)
- Hi(X) ⊗ H2n−i(X) → C,
where n is the (complex) dimension of X. Poincaré duality can also be expressed as a relation of singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
and de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
, by asserting that the map
(integrating a differential k-form over an 2n−k-(real)-dimensional cycle) is a perfect pairing.
The same duality pattern holds for a smooth projective variety over a separably closed field, using l-adic cohomology with Qℓ-coefficients instead. This is further generalized to possibly singular varieties, using intersection cohomology
Intersection cohomology
In topology, a branch of mathematics, intersection homology is an analogue of singular homology especially well-suited for the study of singular spaces, discovered by Mark Goresky and Robert MacPherson in the fall of 1974 and developed by them over the next few years.Intersection cohomology was...
instead, a duality called Verdier duality
Verdier duality
In mathematics, Verdier duality is a generalization of the Poincaré duality of manifolds to locally compact spaces with singularities. Verdier duality was introduced by , as an analog for locally compact spaces of the coherent duality for schemes due to Grothendieck...
. With increasing level of generality, it turns out, an increasing amount of technical background is helpful or necessary to understand these theorems: the modern formulation of both these dualities can be done using derived categories
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
and certain direct and inverse image functors of sheaves
Image functors for sheaves
In mathematics, especially in sheaf theory, a domain applied in areas such as topology, logic and algebraic geometry, there are four image functors for sheaves which belong together in various senses....
, applied to locally constant sheaves (with respect to the classical analytical topology in the first case, and with respect to the étale topology
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
in the second case).
Yet another group of similar duality statements is encountered in arithmetics: étale cohomology of finite
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, local
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
and global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s (also known as Galois cohomology
Galois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
, since étale cohomology over a field is equivalent to group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
of the (absolute) Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the field) admit similar pairings. The absolute Galois group G(Fq) of a finite field, for example, is isomorphic to
, the profinite completion of Z, the integers. Therefore, the perfect pairing (for any G-moduleG-module
In mathematics, given a group G, a G-module is an abelian group M on which G acts compatibly with the abelian group structure on M. This widely applicable notion generalizes that of a representation of G...
M)
- Hn(G, M) × H1−n (G, Hom (M, Q/Z)) → Q/Z
is a direct consequence of Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
of finite groups. For local and global fields, similar statements exist (local duality and global or Poitou–Tate duality).
Serre duality
Serre duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
or coherent duality
Coherent duality
In mathematics, coherent duality is any of a number of generalisations of Serre duality, applying to coherent sheaves, in algebraic geometry and complex manifold theory, as well as some aspects of commutative algebra that are part of the 'local' theory....
are similar to the statements above, but applies to cohomology of coherent sheaves instead.
- Alexander dualityAlexander dualityIn mathematics, Alexander duality refers to a duality theory presaged by a result of 1915 by J. W. Alexander, and subsequently further developed, particularly by P. S. Alexandrov and Lev Pontryagin...
See also
- List of dualities
- Duality principle (disambiguation)
- Dual (category theory)Dual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
- Dual numberDual numberIn linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
s, a certain associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
; the term "dual" here is synonymous with double, and is unrelated to the notions given above. - Duality (electrical engineering)Duality (electrical engineering)In electrical engineering, electrical terms are associated into pairs called duals. A dual of a relationship is formed by interchanging voltage and current in an expression...
- Lagrange duality
- Dual code
- Dual lattice
- Dual basis
- dual abelian varietyDual abelian varietyIn mathematics, a dual abelian variety can be defined from an abelian variety A, defined over a field K.-Definition:To an abelian variety A over a field k, one associates a dual abelian variety Av , which is the solution to the following moduli problem...
- Adjoint functors