
Intersection (set theory)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
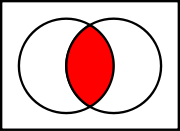
, the intersection (denoted as ∩) of two sets A and B is the set that contains all elements of A that also belong to B (or equivalently, all elements of B that also belong to A), but no other elements.
For explanation of the symbols used in this article, refer to the table of mathematical symbols
Table of mathematical symbols
This is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...
.
Basic definition
The intersection of A and B is written "A ∩ B".Formally:
- x ∈ A ∩ B if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
- x ∈ A andLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
- x ∈ B.
- x ∈ A and
- For example:
- The intersection of the sets {1, 2, 3} and {2, 3, 4} is {2, 3}.
- The number 9 is not in the intersection of the set of prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s {2, 3, 5, 7, 11, …} and the set of odd numbers {1, 3, 5, 7, 9, 11, …}.
If the intersection of two sets A and B is empty, that is they have no elements in common, then they are said to be disjoint, denoted: A ∩ B = ∅. For example the sets {1, 2} and {3, 4} are disjoint, written
{1, 2} ∩ {3, 4} = ∅.
More generally, one can take the intersection of several sets at once.
The intersection of A, B, C, and D, for example, is A ∩ B ∩ C ∩ D = A ∩ (B ∩ (C ∩ D)).
Intersection is an associative operation; thus,
A ∩ (B ∩ C) = (A ∩ B) ∩ C.
If the sets A and B are closed under complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
then the intersection of A and B may be written as the complement of the union of their complements, derived easily from De Morgan's laws:
A ∩ B = (Ac ∪ Bc)c
Arbitrary intersections
The most general notion is the intersection of an arbitrary nonempty collection of sets.If M is a nonempty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
set whose elements are themselves sets, then x is an element of the intersection of M if and only if for every
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
element A of M, x is an element of A.
In symbols:

The notation for this last concept can vary considerably.
Set theorists
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
will sometimes write "M", while others will instead write "A∈M A".
The latter notation can be generalized to "i∈I Ai", which refers to the intersection of the collection {Ai : i ∈ I}.
Here I is a nonempty set, and Ai is a set for every i in I.
In the case that the index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
I is the set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, notation analogous to that of an infinite series may be seen:
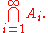
When formatting is difficult, this can also be written "A1 ∩ A2 ∩ A3 ∩ ...", even though strictly speaking, A1 ∩
(This last example, an intersection of countably many sets, is actually very common; for an example see the article on σ-algebras.)
Finally, let us note that whenever the symbol "∩" is placed before other symbols instead of between them, it should be of a larger size .
Nullary intersection
Note that in the previous section we excluded the case where M was the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
. The reason is as follows: The intersection of the collection M is defined as the set (see set-builder notation
Set-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
)
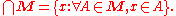
If M is empty there are no sets A in M, so the question becomes "which x
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
. So the intersection of the empty family should be the universal set
Universal set
In set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
, which according to standard (ZFC
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
) set theory, does not exist.
A partial fix for this problem can be found if we agree to restrict our attention to subsets of a fixed set U called the universe. In this case the intersection of a family of subsets of U can be defined as

Now if M is empty there is no problem. The intersection is just the entire universe U, which is a well-defined set by assumption.
See also
- ComplementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
- Intersection graphIntersection graphIn the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
- Logical conjunctionLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
- Naive set theoryNaive set theoryNaive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
- Symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
- UnionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
- Cardinality
- Iterated binary operationIterated binary operationIn mathematics, an iterated binary operation is an extension of a binary operation on a set S to a function on finite sequences of elements of S through repeated application. Common examples include the extension of the addition operation to the summation operation, and the extension of the...

