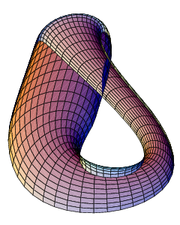
Klein bottle - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Klein bottle (icon) is a non-orientable

Orientability

In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...

surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

, informally, a surface (a two-dimensional manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

) in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip

Möbius strip

The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...

and the real projective plane

Real projective plane

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...

. Whereas a Möbius strip is a surface with boundary, a Klein bottle has no boundary. (For comparison, a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

is an orientable surface with no boundary.)

The Klein bottle was first described in 1882 by the German

Germany

Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...

mathematician Felix Klein

Felix Klein

Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...

. It is sometimes claimed that it was originally named the Kleinsche Fläche "Klein surface" and that this was incorrectly interpreted as Kleinsche Flasche "Klein bottle," which ultimately led to the adoption of this term in the German language as well.

Construction

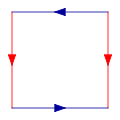
Start with a square, and then glue together corresponding coloured edges, in the following diagram, so that the arrows match. More formally, the Klein bottle is the quotient space

Quotient space

In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...

described as the square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

[0,1] × [0,1] with sides identified by the relations for and for :

This square is a fundamental polygon

Fundamental polygon

In mathematics, each closed surface in the sense of geometric topology can be constructed from an even-sided oriented polygon, called a fundamental polygon, by pairwise identification of its edges....

of the Klein bottle.

Note that this is an "abstract" gluing in the sense that trying to realize this in three dimensions results in a self-intersecting Klein bottle. The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions.

Glue the red arrows of the square together (left and right sides), resulting in a cylinder. To glue the ends together so that the arrows on the circles match, pass one end through the side of the cylinder. Note that this creates a circle of self-intersection. This is an immersion of the Klein bottle in three dimensions.
By adding a fourth dimension to the three dimensional space, the self-intersection can be eliminated. Gently push a piece of the tube containing the intersection out of the original three dimensional space. A useful analogy is to consider a self-intersecting curve on the plane; self-intersections can be eliminated by lifting one strand off the plane.

This immersion is useful for visualizing many properties of the Klein bottle. For example, the Klein bottle has no boundary, where the surface stops abruptly, and it is non-orientable

Orientability

, as reflected in the one-sidedness of the immersion.

The common physical model of a Klein bottle is a similar construction. The Science Museum in London

Science Museum (London)

The Science Museum is one of the three major museums on Exhibition Road, South Kensington, London in the Royal Borough of Kensington and Chelsea. It is part of the National Museum of Science and Industry. The museum is a major London tourist attraction....

has on display a collection of hand-blown glass Klein bottles, exhibiting many variations on this topological theme. The bottles date from 1995 and were made for the museum by Alan Bennett.

Properties

The Klein bottle can be seen as a fiber bundle

Fiber bundle

In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...

over S¹ as follows: one takes the square (modulo the edge identifying equivalence relation) from above to be E, the total space, while the base space B is given by the unit interval in y, modulo 1~0. The projection π is then given by π([x, y]) = [y].

Like the Möbius strip

Möbius strip

, the Klein bottle is a two-dimensional differentiable manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

which is not orientable

Orientability

. Unlike the Möbius strip, the Klein bottle is a closed manifold, meaning it is a compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

manifold without boundary. While the Möbius strip can be embedded in three-dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

R³, the Klein bottle cannot. It can be embedded in R⁴, however.

The Klein bottle can be constructed (in a mathematical sense, because it cannot be done without allowing the surface to intersect itself) by joining the edges of two Möbius strips together, as described in the following anonymous

Anonymity

Anonymity is derived from the Greek word ἀνωνυμία, anonymia, meaning "without a name" or "namelessness". In colloquial use, anonymity typically refers to the state of an individual's personal identity, or personally identifiable information, being publicly unknown.There are many reasons why a...

limerick

Limerick (poetry)

A limerick is a kind of a witty, humorous, or nonsense poem, especially one in five-line or meter with a strict rhyme scheme , which is sometimes obscene with humorous intent. The form can be found in England as of the early years of the 18th century...

A mathematician named Klein

Thought the Möbius band was divine.

Said he: "If you glue

The edges of two,

You'll get a weird bottle like mine."

Six colors suffice to color any map on the surface of a Klein bottle; this is the only exception to
the Heawood conjecture

Heawood conjecture

In graph theory, the Heawood conjecture or Ringel–Youngs theorem gives a lower bound for the number of colors that are necessary for graph coloring on a surface of a given genus. It was proven in 1968 by Gerhard Ringel and John W. T. Youngs. One case, the non-orientable Klein bottle, proved an...

, a generalization of the four color theorem

Four color theorem

In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...

, which would require seven.

A Klein bottle is equivalent to a sphere plus two cross caps.

When embedded in Euclidean space the Klein bottle is one-sided. However there are other topological 3-spaces, and in some of the non-orientable examples a Klein bottle can be embedded such that it is two-sided, though due to the nature of the space it remains non-orientable.

Dissection

Dissecting a Klein bottle into halves along its plane of symmetry results in two mirror image Möbius strip

Möbius strip

s, i.e. one with a left-handed half-twist and the other with a right-handed half-twist (one of these is pictured on the right). Remember that the intersection pictured isn't really there.

Simple-closed curves

One description of the types of simple-closed curves that may appear on the surface of the Klein bottle is given by the use of the first homology group of the Klein bottle calculated with integer coefficients. This group is isomorphic to Z×Z₂. Up to reversal of orientation, the only homology classes which contain simple-closed curves are as follows: (0,0), (1,0), (1,1), (2,0), (0,1). Up to reversal of the orientation of a simple closed curve, if it lies within one of the two crosscaps that make up the Klein bottle, then it is in homology class (1,0) or (1,1); if it cuts the Klein bottle into two Möbius bands, then it is in homology class (2,0); if it cuts the Klein bottle into an annulus, then it is in homology class (0,1); and if bounds a disk, then it is in homology class (0,0).

Parameterization

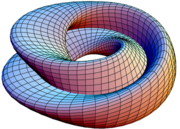
The "figure 8" immersion (Klein bagel) of the Klein bottle has a particularly simple parameterization. It is that of a "figure-8" torus with a 180 degree "Möbius" twist inserted:

In this immersion, the self-intersection circle is a geometric circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

in the xy-plane. The positive constant r is the radius of this circle. The parameter u gives the angle in the xy-plane, and v specifies the position around the 8-shaped cross section. With the above parameterization the cross section is a 2:1 Lissajous curve

Lissajous curve

In mathematics, a Lissajous curve , also known as Lissajous figure or Bowditch curve, is the graph of a system of parametric equationswhich describe complex harmonic motion...

.

The parameterization of the 3-dimensional immersion of the bottle itself is much more complicated. Here is a simplified version:

where

for 0 ≤ u < 2π and 0 ≤ v < 2π.

In this parameterization, u follows the length of the bottle's body while v goes around its circumference.

Generalizations

The generalization of the Klein bottle to higher genus

Genus (mathematics)

In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...

is given in the article on the fundamental polygon

Fundamental polygon

.

In another order of ideas, constructing 3-manifold

3-manifold

In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...

s, it is known that a solid Klein bottle is topologically equivalent with the Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

, the Mobius band

Mobius Band

Mobius Band is an electronic rock trio from Brooklyn, New York consisting of Noam Schatz , Peter Sax , and Ben Sterling .-History:...

times an interval. The solid Klein bottle is the non-orientable version of the solid torus, equivalent to

Klein surface

A Klein surface is, as for Riemann surface

Riemann surface

In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...

s, a surface with an atlas allowing the transition function

Transition function

In mathematics, a transition function has several different meanings:* In topology, a transition function is a homeomorphism from one coordinate chart to another...

s to be composed using complex conjugation. One can obtain the so called dianalytic structure of the space.

External links

Imaging Maths - The Klein Bottle
The biggest Klein bottle in all the world
Klein Bottle animation: produced for a topology seminar at the Leibniz University Hannover. http://www-ifm.math.uni-hannover.de/~fugru/video/top/05_top_Kleins_Bottle.mov
Klein Bottle animation from 2010 including a car ride through the bottle and the original description by Felix Klein: produced at the Free University Berlin.
Torus Games Free downloadable games for Windows and Mac OS X that highlight the topologies of the Torus and Klein Bottle.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Construction

Properties

Dissection

Simple-closed curves

Parameterization

Generalizations

Klein surface

See also

External links