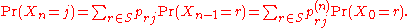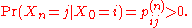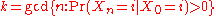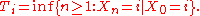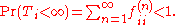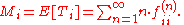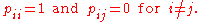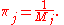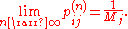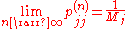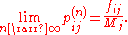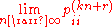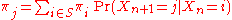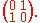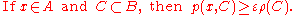Markov chain
Encyclopedia
A Markov chain, named after Andrey Markov
, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process
characterized as memoryless
: the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property
. Markov chains have many applications as statistical models of real-world processes.
with the Markov property
. Often, the term "Markov chain" is used to mean a Markov process which has a discrete (finite or countable) state-space. Usually a Markov chain is defined for a discrete set of times (i.e., a discrete-time Markov chain) although some authors use the same terminology where "time" can take continuous values. The use of the term in Markov chain Monte Carlo
methodology covers cases where the process is in discrete time (discrete algorithm steps) with a continuous state space. The following concentrates on the discrete-time discrete-state-space case.
A discrete-time random process involves a system which is in a certain state at each step, with the state changing randomly between steps. The steps are often thought of as moments in time, but they can equally well refer to physical distance or any other discrete measurement; formally, the steps are the integers or natural numbers, and the random process is a mapping of these to states. The Markov property states that the conditional probability distribution for the system at the next step (and in fact at all future steps) depends only on the current state of the system, and not additionally on the state of the system at previous steps.
Since the system changes randomly, it is generally impossible to predict with certainty the state of a Markov chain at a given point in the future. However, the statistical properties of the system's future can be predicted. In many applications, it is these statistical properties that are important.
The changes of state of the system are called transitions, and the probabilities associated with various state-changes are called transition probabilities. The set of all states and transition probabilities completely characterizes a Markov chain. By convention, we assume all possible states and transitions have been included in the definition of the processes, so there is always a next state and the process goes on forever.
A famous Markov chain is the so-called "drunkard's walk", a random walk
on the number line
where, at each step, the position may change by +1 or −1 with equal probability. From any position there are two possible transitions, to the next or previous integer. The transition probabilities depend only on the current position, not on the manner in which the position was reached. For example, the transition probabilities from 5 to 4 and 5 to 6 are both 0.5, and all other transition probabilities from 5 are 0. These probabilities are independent of whether the system was previously in 4 or 6.
Another example is the dietary habits of a creature who eats only grapes, cheese or lettuce, and whose dietary habits conform to the following rules:
This creature's eating habits can be modeled with a Markov chain since its choice tomorrow depends solely on what it ate today, not what it ate yesterday or even farther in the past. One statistical property that could be calculated is the expected percentage, over a long period, of the days on which the creature will eat grapes.
A series of independent events (for example, a series of coin flips) satisfies the formal definition of a Markov chain. However, the theory is usually applied only when the probability distribution of the next step depends non-trivially on the current state.
Many other examples of Markov chains
exist.
s X1, X2, X3, ... with the Markov property, namely that, given the present state, the future and past states are independent. Formally,
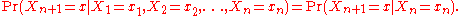
The possible values of Xi form a countable set
S called the state space of the chain.
Markov chains are often described by a directed graph
, where the edges are labeled by the probabilities of going from one state to the other states.
Andrey Markov
Andrey Andreyevich Markov was a Russian mathematician. He is best known for his work on theory of stochastic processes...
, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
characterized as memoryless
Memorylessness
In probability and statistics, memorylessness is a property of certain probability distributions: the exponential distributions of non-negative real numbers and the geometric distributions of non-negative integers....
: the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
. Markov chains have many applications as statistical models of real-world processes.
Introduction
Formally, a Markov chain is a discrete (discrete-time) random processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
with the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
. Often, the term "Markov chain" is used to mean a Markov process which has a discrete (finite or countable) state-space. Usually a Markov chain is defined for a discrete set of times (i.e., a discrete-time Markov chain) although some authors use the same terminology where "time" can take continuous values. The use of the term in Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
methodology covers cases where the process is in discrete time (discrete algorithm steps) with a continuous state space. The following concentrates on the discrete-time discrete-state-space case.
A discrete-time random process involves a system which is in a certain state at each step, with the state changing randomly between steps. The steps are often thought of as moments in time, but they can equally well refer to physical distance or any other discrete measurement; formally, the steps are the integers or natural numbers, and the random process is a mapping of these to states. The Markov property states that the conditional probability distribution for the system at the next step (and in fact at all future steps) depends only on the current state of the system, and not additionally on the state of the system at previous steps.
Since the system changes randomly, it is generally impossible to predict with certainty the state of a Markov chain at a given point in the future. However, the statistical properties of the system's future can be predicted. In many applications, it is these statistical properties that are important.
The changes of state of the system are called transitions, and the probabilities associated with various state-changes are called transition probabilities. The set of all states and transition probabilities completely characterizes a Markov chain. By convention, we assume all possible states and transitions have been included in the definition of the processes, so there is always a next state and the process goes on forever.
A famous Markov chain is the so-called "drunkard's walk", a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
on the number line
Number line
In basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...
where, at each step, the position may change by +1 or −1 with equal probability. From any position there are two possible transitions, to the next or previous integer. The transition probabilities depend only on the current position, not on the manner in which the position was reached. For example, the transition probabilities from 5 to 4 and 5 to 6 are both 0.5, and all other transition probabilities from 5 are 0. These probabilities are independent of whether the system was previously in 4 or 6.
Another example is the dietary habits of a creature who eats only grapes, cheese or lettuce, and whose dietary habits conform to the following rules:
- It eats exactly once a day.
- If it ate cheese today, tomorrow it will eat lettuce or grapes with equal probability.
- If it ate grapes today, tomorrow it will eat grapes with probability 1/10, cheese with probability 4/10 and lettuce with probability 5/10.
- If it ate lettuce today, it will not eat lettuce again tomorrow but will eat grapes with probability 4/10 or cheese with probability 6/10.
This creature's eating habits can be modeled with a Markov chain since its choice tomorrow depends solely on what it ate today, not what it ate yesterday or even farther in the past. One statistical property that could be calculated is the expected percentage, over a long period, of the days on which the creature will eat grapes.
A series of independent events (for example, a series of coin flips) satisfies the formal definition of a Markov chain. However, the theory is usually applied only when the probability distribution of the next step depends non-trivially on the current state.
Many other examples of Markov chains
Examples of Markov chains
- Board games played with dice :A game of snakes and ladders or any other game whose moves are determined entirely by dice is a Markov chain, indeed, an absorbing Markov chain. This is in contrast to card games such as blackjack, where the cards represent a 'memory' of the past moves. To see the...
exist.
Formal definition
A Markov chain is a sequence of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X1, X2, X3, ... with the Markov property, namely that, given the present state, the future and past states are independent. Formally,
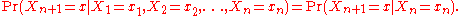
The possible values of Xi form a countable set
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
S called the state space of the chain.
Markov chains are often described by a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, where the edges are labeled by the probabilities of going from one state to the other states.
Variations
- Continuous-time Markov processes have a continuous index.Time-homogeneous Markov chains (or stationary Markov chains) are processes where
- for all n. The probability of the transition is independent of n.
- A Markov chain of order m (or a Markov chain with memory m), where m is finite, is a process satisfying
-
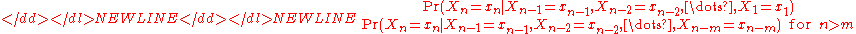
- In other words, the future state depends on the past m states. It is possible to construct a chain (Yn) from (Xn) which has the 'classical' Markov property as follows:
- Let Yn = (Xn, Xn−1, ..., Xn−m+1), the ordered m-tuple of X values. Then Yn is a Markov chain with state space Sm and has the classical Markov propertyMarkov propertyIn probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
.
It can be proved that a Markov chain of order m can be in fact reduced to a Markov chain of order m = 1 (a simple Markov chain).
- An additive Markov chainAdditive Markov chainIn probability theory, an additive Markov chain is a Markov chain with an additive conditional probability function. Here the process is a discrete-time Markov chain of order m and the transition probability to a state at the next time is a sum of functions, each depending on the next state and one...
of order m is determined by an additive conditional probability,
The value f(xn,xn-r,r) is the additive contribution of the variable xn-r to the conditional probability.
Example
A simple example is shown in the figure on the right, using a directed graph to picture the state transitions. The states represent whether the economy is in a bull market, a bear market, or a recession, during a given week. According to the figure, a bull week is followed by another bull week 90% of the time, a bear market 7.5% of the time, and a recession the other 2.5%. From this figure it is possible to calculate, for example, the long-term fraction of time during which the economy is in a recession, or on average how long it will take to go from a recession to a bull market.
A thorough development and many examples can be found in the on-line monograph
Meyn & Tweedie 2005.
The appendix of Meyn 2007, also available on-line, contains an abridged Meyn & Tweedie.
A finite state machineFinite state machineA finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
can be used as a representation of a Markov chain. Assuming a sequence of independent and identically distributedIndependent and identically distributed random variablesIn probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
input signals (for example, symbols from a binary alphabet chosen by coin tosses), if the machine is in state y at time n, then the probability that it moves to state x at time n + 1 depends only on the current state.
Markov chains
The probability of going from state i to state j in n time steps is
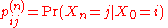
and the single-step transition is

For a time-homogeneous Markov chain:
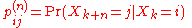
and
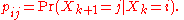
The n-step transition probabilities satisfy the Chapman–Kolmogorov equation, that for any k such that 0 < k < n,

where S is the state space of the Markov chain.
The marginal distributionMarginal distributionIn probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
Pr(Xn = x) is the distribution over states at time n. The initial distribution is Pr(X0 = x). The evolution of the process through one time step is described by
Note: The superscript (n) is an indexIndex (mathematics)The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
and not an exponent.
Reducibility
A state j is said to be accessible from a state i (written i → j) if a system started in state i has a non-zero probability of transitioning into state j at some point. Formally, state j is accessible from state i if there exists an integer n ≥ 0 such that
Allowing n to be zero means that every state is defined to be accessible from itself.
A state i is said to communicate with state j (written i ↔ j) if both i → j and j → i. A set of states C is a communicating class if every pair of states in C communicates with each other, and no state in C communicates with any state not in C. It can be shown that communication in this sense is an equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
and thus that communicating classes are the equivalence classes of this relation. A communicating class is closed if the probability of leaving the class is zero, namely that if i is in C but j is not, then j is not accessible from i.
That said, communicating classes need not be commutative, in that classes achieving greater periodic frequencies that encompass 100% of the phases of smaller periodic frequencies, may still be communicating classes provided a form of either diminished, downgraded, or multiplexed cooperation exists within the higher frequency class.
A state i is said to be essential if for all j such that i → j it is also true that j → i. A state i is inessential if it is not essential.
Finally, a Markov chain is said to be irreducible if its state space is a single communicating class; in other words, if it is possible to get to any state from any state.
Periodicity
A state i has period k if any return to state i must occur in multiples of k time steps. Formally, the periodPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
of a state is defined as
(where "gcd" is the greatest common divisorGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
). Note that even though a state has period k, it may not be possible to reach the state in k steps. For example, suppose it is possible to return to the state in {6, 8, 10, 12, ...} time steps; k would be 2, even though 2 does not appear in this list.
If k = 1, then the state is said to be aperiodic: returns to state i can occur at irregular times. Otherwise (k > 1), the state is said to be periodic with period k.
It can be shown that every state in a communicating class must have overlapping periods with all equivalent-or-larger occurring sample(s).
Every state of a bipartite graphBipartite graphIn the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
has an even period.
Recurrence
A state i is said to be transient if, given that we start in state i, there is a non-zero probability that we will never return to i. Formally, let the random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
Ti be the first return time to state i (the "hitting time"):
The number
is the probability that we return to state i for the first time after n steps.
Therefore, state i is transient if
State i is recurrent (or persistent) if it is not transient.
Recurrent states have finite hitting time with probability 1.
Mean recurrence time
Even if the hitting time is finite with probability 1, it need not have a finite expectationExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
.
The mean recurrence time at state i is the expected return time Mi:
State i is positive recurrent (or non-null persistent) if Mi is finite; otherwise, state i is null recurrent (or null persistent).
Expected number of visits
It can be shown that a state i is recurrent if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the expected number of visits to this state is infinite, i.e.,
Absorbing states
A state i is called absorbing if it is impossible to leave this state. Therefore, the state i is absorbing if and only if
If every state can reach an absorbing state, then the Markov chain is an absorbing Markov chainAbsorbing Markov chainIn the mathematical theory of probability, an absorbing Markov chain is a Markov chain in which every state can reach an absorbing state. An absorbing state is a state that, once entered, cannot be left....
.
Ergodicity
A state i is said to be ergodicErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
if it is aperiodic and positive recurrent. If all states in an irreducible Markov chain are ergodic, then the chain is said to be ergodic.
It can be shown that a finite state irreducible Markov chain is ergodic if it has an aperiodic state. A model has the ergodic property if there's a finite number N such that any state can be reached from any other state in exactly N steps. In case of a fully connected transition matrix where all transitions have a non-zero probability, this condition is fulfilled with N=1. A model with more than one state and just one out-going transition per state cannot be ergodic.
Steady-state analysis and limiting distributions
If the Markov chain is a time-homogeneous Markov chain, so that the process is described by a single, time-independent matrix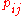 , then the vector
, then the vector 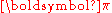 is called a stationary distribution (or invariant measureInvariant measureIn mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
is called a stationary distribution (or invariant measureInvariant measureIn mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
) if its entries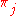 are non-negative and sum to 1 and if it satisfies
are non-negative and sum to 1 and if it satisfies
An irreducible chain has a stationary distribution if and only if all of its states are positive recurrent. In that case, π is unique and is related to the expected return time:
Further, if the chain is both irreducible and aperiodic, then for any i and j,
Note that there is no assumption on the starting distribution; the chain converges to the stationary distribution regardless of where it begins. Such π is called the equilibrium distribution of the chain.
If a chain has more than one closed communicating class, its stationary distributions will not be unique (consider any closed communicating class in the chain; each one will have its own unique stationary distribution
in the chain; each one will have its own unique stationary distribution 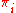 . Extending these distributions to the overall chain, setting all values to zero outside the communication class, yields that the set of invariant measures of the original chain is the set of all convex combinations of the
. Extending these distributions to the overall chain, setting all values to zero outside the communication class, yields that the set of invariant measures of the original chain is the set of all convex combinations of the 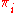 's). However, if a state j is aperiodic, then
's). However, if a state j is aperiodic, then
and for any other state i, let fij be the probability that the chain ever visits state j if it starts at i,
If a state i is periodic with period k > 1 then the limit
does not exist, although the limit
does exist for every integer r.
Steady-state analysis and the time-inhomogeneous Markov chain
A Markov chain need not necessarily be time-homogeneous to have an equilibrium distribution. If there is a probability distribution over states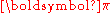 such that
such that
for every state j and every time n then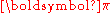 is an equilibrium distribution of the Markov chain. Such can occur in Markov chain Monte Carlo (MCMC)Markov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
is an equilibrium distribution of the Markov chain. Such can occur in Markov chain Monte Carlo (MCMC)Markov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
methods in situations where a number of different transition matrices are used, because each is efficient for a particular kind of mixing, but each matrix respects a shared equilibrium distribution.
Finite state space
If the state space is finite, the transition probability distribution can be represented by a matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, called the transition matrix, with the (i, j)th element of P equal to
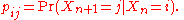
Since each row of P sums to one and all elements are non-negative, P is a right stochastic matrix.
Time-homogeneous Markov chain with a finite state space
If the Markov chain is time-homogeneous, then the transition matrix P is the same after each step, so the k-step transition probability can be computed as the k-th power of the transition matrix, Pk.
The stationary distribution π is a (row) vector, whose entries are non-negative and sum to 1, that satisfies the equation

In other words, the stationary distribution π is a normalized (meaning that the sum of its entries is 1) left eigenvector of the transition matrix associated with the eigenvalue 1.
Alternatively, π can be viewed as a fixed point of the linear (hence continuous) transformation on the unit simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
associated to the matrix P. As any continuous transformation in the unit simplex has a fixed point, a stationary distribution always exists, but is not guaranteed to be unique, in general. However, if the Markov chain is irreducible and aperiodic, then there is a unique stationary distribution π. Additionally, in this case Pk converges to a rank-one matrix in which each row is the stationary distribution π, that is,

where 1 is the column vector with all entries equal to 1. This is stated by the Perron–Frobenius theoremPerron–Frobenius theoremIn linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
. If, by whatever means,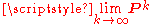 is found, then the stationary distribution of the Markov chain in question can be easily determined for any starting distribution, as will be explained below.
is found, then the stationary distribution of the Markov chain in question can be easily determined for any starting distribution, as will be explained below.
For some stochastic matrices P, the limit does not exist, as shown by this example:
does not exist, as shown by this example:
Because there are a number of different special cases to consider, the process of finding this limit if it exists can be a lengthy task. However, there are many techniques that can assist in finding this limit. Let P be an n×n matrix, and define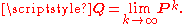
It is always true that
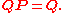
Subtracting Q from both sides and factoring then yields
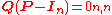
where In is the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
of size n, and 0n,n is the zero matrix of size n×n. Multiplying together stochastic matrices always yields another stochastic matrix, so Q must be a stochastic matrixStochastic matrixIn mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
. It is sometimes sufficient to use the matrix equation above and the fact that Q is a stochastic matrix to solve for Q. Including the fact that the sum of each the rows in P is 1, there are n+1 equations for determining n unknowns, so it is computationally easier if on the one hand one selects one row in Q and substitute each of its elements by one, and on the other one substitute the corresponding element (the one in the same column) in the vector 0, and next left-multiply this latter vector by the inverse of transformed former matrix to find Q.
Here is one method for doing so: first, define the function f(A) to return the matrix A with its right-most column replaced with all 1's. If [f(P − In)]−1 exists then
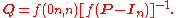
- Explain: The original matrix equation is equivalent to a system of n×n linear equations in n×n variables. And there are n more linear equations from the fact that Q is a right stochastic matrixStochastic matrixIn mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
whose each row sums to 1. So it needs any n×n independent linear equations of the (n×n+n) equations to solve for the n×n variables. In this example, the n equations from “Q multiplied by the right-most column of (P-In)” have been replaced by the n stochastic ones.
One thing to notice is that if P has an element Pi,i on its main diagonal that is equal to 1 and the ith row or column is otherwise filled with 0's, then that row or column will remain unchanged in all of the subsequent powers Pk. Hence, the ith row or column of Q will have the 1 and the 0's in the same positions as in P.
Reversible Markov chain
A Markov chain is said to be reversible if there is a probability distribution over states, π, such that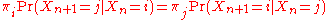
for all times n and all states i and j.
This condition is also known as the detailed balanceDetailed balanceThe principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
condition (some books refer the local balance equation).
With a time-homogeneous Markov chain, Pr(Xn+1 = j | Xn = i) does not change with time n and it can be written more simply as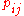 . In this case, the detailed balance equation can be written more compactly as
. In this case, the detailed balance equation can be written more compactly as
Summing the original equation over i gives
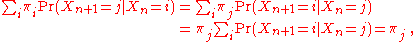
so, for reversible Markov chains, π is always a steady-state distribution of Pr(Xn+1 = j | Xn = i) for every n.
If the Markov chain begins in the steady-state distribution, i.e., if Pr(X0 = i) = πi, then Pr(Xn = i) = πi for all n and the detailed balance equation can be written as
The left- and right-hand sides of this last equation are identical except for a reversing of the time indices n and n + 1.
Reversible Markov chains are common in Markov chain Monte Carlo (MCMC)Markov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
approaches because the detailed balance equation for a desired distribution π necessarily implies that the Markov chain has been constructed so that π is a steady-state distribution. Even with time-inhomogeneous Markov chains, where multiple transition matrices are used, if each such transition matrix exhibits detailed balance with the desired π distribution, this necessarily implies that π is a steady-state distribution of the Markov chain.
Bernoulli scheme
A Bernoulli schemeBernoulli schemeIn mathematics, the Bernoulli scheme or Bernoulli shift is a generalization of the Bernoulli process to more than two possible outcomes. Bernoulli schemes are important in the study of dynamical systems, as most such systems exhibit a repellor that is the product of the Cantor set and a smooth...
is a special case of a Markov chain where the transition probability matrix has identical rows, which means that the next state is even independent of the current state (in addition to being independent of the past states). A Bernoulli scheme with only two possible states is known as a Bernoulli processBernoulli processIn probability and statistics, a Bernoulli process is a finite or infinite sequence of binary random variables, so it is a discrete-time stochastic process that takes only two values, canonically 0 and 1. The component Bernoulli variables Xi are identical and independent...
.
General state space
Many results for Markov chains with finite state space can be generalized to chains with uncountable state space through Harris chains. The main idea is to see if there is a point in the state space that the chain hits with probability one. Generally, it is not true for continuous state space, however, we can define sets A and B along with a positive number ε and a probability
measure ρ, such that
Then we could collapse the sets into an auxiliary point α, and a recurrent Harris chain can be modified to contain α. Lastly, the collection of Harris chains is a comfortable level of generality, which is broad enough to contain a large number of interesting examples, yet restrictive enough to allow for a rich theory.
Applications
Markov chains are applied in a number of ways to many different fields. Often they are used as a mathematical model from some random physical process; if the parameters of the chain are known, quantitative predictions can be made. In other cases, they are used to model a more abstract process, and are the theoretical underpinning of an algorithm.
Physics
Markovian systems appear extensively in thermodynamicsThermodynamicsThermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
and statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, whenever probabilities are used to represent unknown or unmodelled details of the system, if it can be assumed that the dynamics are time-invariant, and that no relevant history need be considered which is not already included in the state description.
Chemistry
Chemistry is often a place where Markov chains and continuous-time Markov processes are especially useful because these simple physical systems tend to satisfy the Markov property quite well. The classical model of enzyme activity, Michaelis-Menten kinetics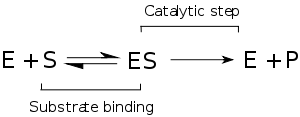 Michaelis-Menten kineticsIn biochemistry, Michaelis–Menten kinetics is one of the simplest and best-known models of enzyme kinetics. It is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten. The model takes the form of an equation describing the rate of enzymatic reactions, by relating...
Michaelis-Menten kineticsIn biochemistry, Michaelis–Menten kinetics is one of the simplest and best-known models of enzyme kinetics. It is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten. The model takes the form of an equation describing the rate of enzymatic reactions, by relating...
, can be viewed as a Markov chain, where at each time step the reaction proceeds in some direction. While Michaelis-Menten is fairly straightforward, far more complicated reaction networks can also be modeled with Markov chains.
An algorithm based on a Markov chain was also used to focus the fragment-based growth of chemicals in silico towards a desired class of compounds such as drugs or natural products. As a molecule is grown, a fragment is selected from the nascent molecule as the "current" state. It is not aware of its past (i.e., it is not aware of what is already bonded to it). It then transitions to the next state when a fragment is attached to it. The transition probabilities are trained on databases of authentic classes of compounds.
Also, the growth (and composition) of copolymers may be modeled using Markov chains. Based on the reactivity ratios of the monomers that make up the growing polymer chain, the chain's composition may be calculated (e.g., whether monomers tend to add in alternating fashion or in long runs of the same monomer). Due to steric effectsSteric effectsSteric effects arise from the fact that each atom within a molecule occupies a certain amount of space. If atoms are brought too close together, there is an associated cost in energy due to overlapping electron clouds , and this may affect the molecule's preferred shape and reactivity.-Steric...
, second-order Markov effects may also play a role in the growth of some polymer chains.
Testing
Several theorists have proposed the idea of the Markov chain statistical test (MCST), a method of conjoining Markov chains to form a "Markov blanketMarkov blanketIn machine learning, the Markov blanket for a node A in a Bayesian network is the set of nodes \partial A composed of A's parents, its children, and its children's other parents. In a Markov network, the Markov blanket of a node is its set of neighbouring nodes...
", arranging these chains in several recursive layers ("wafering") and producing more efficient test sets—samples—as a replacement for exhaustive testing. MCSTs also have uses in temporal state-based networks; Chilukuri et al.'s paper entitled "Temporal Uncertainty Reasoning Networks for Evidence Fusion with Applications to Object Detection and Tracking" (ScienceDirect) gives a background and case study for applying MCSTs to a wider range of applications.
Information sciences
Markov chains are used throughout information processing. Claude Shannon's famous 1948 paper A mathematical theory of communicationA Mathematical Theory of Communication"A Mathematical Theory of Communication" is an influential 1948 article by mathematician Claude E. Shannon. As of November 2011, Google Scholar has listed more than 48,000 unique citations of the article and the later-published book version...
, which in a single step created the field of information theoryInformation theoryInformation theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, opens by introducing the concept of entropyInformation entropyIn information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
through Markov modeling of the English language. Such idealized models can capture many of the statistical regularities of systems. Even without describing the full structure of the system perfectly, such signal models can make possible very effective data compressionData compressionIn computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
through entropy encodingEntropy encodingIn information theory an entropy encoding is a lossless data compression scheme that is independent of the specific characteristics of the medium....
techniques such as arithmetic codingArithmetic codingArithmetic coding is a form of variable-length entropy encoding used in lossless data compression. Normally, a string of characters such as the words "hello there" is represented using a fixed number of bits per character, as in the ASCII code...
. They also allow effective state estimation and pattern recognitionPattern recognitionIn machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
.
Markov chains are also the basis for Hidden Markov Models, which are an important tool in such diverse fields as telephone networks (for error correction), speech recognition and bioinformaticsBioinformaticsBioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
.
The world's mobile telephone systems depend on the Viterbi algorithmViterbi algorithmThe Viterbi algorithm is a dynamic programming algorithm for finding the most likely sequence of hidden states – called the Viterbi path – that results in a sequence of observed events, especially in the context of Markov information sources, and more generally, hidden Markov models...
for error-correction, while hidden Markov models are extensively used in speech recognitionSpeech recognitionSpeech recognition converts spoken words to text. The term "voice recognition" is sometimes used to refer to recognition systems that must be trained to a particular speaker—as is the case for most desktop recognition software...
and also in bioinformaticsBioinformaticsBioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
, for instance for coding region/gene prediction. Markov chains also play an important role in reinforcement learningReinforcement learningInspired by behaviorist psychology, reinforcement learning is an area of machine learning in computer science, concerned with how an agent ought to take actions in an environment so as to maximize some notion of cumulative reward...
.
Queueing theory
Markov chains are the basis for the analytical treatment of queues (queueing theoryQueueing theoryQueueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
). This makes them critical for optimizing the performance of telecommunications networks, where messages must often compete for limited resources (such as bandwidth).
Internet applications
The PageRankPageRankPageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
of a webpage as used by GoogleGoogleGoogle Inc. is an American multinational public corporation invested in Internet search, cloud computing, and advertising technologies. Google hosts and develops a number of Internet-based services and products, and generates profit primarily from advertising through its AdWords program...
is defined by a Markov chain. It is the probability to be at page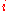 in the stationary distribution on the following Markov chain on all (known) webpages. If
in the stationary distribution on the following Markov chain on all (known) webpages. If  is the number of known webpages, and a page
is the number of known webpages, and a page 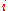 has
has 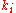 links then it has transition probability
links then it has transition probability 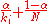 for all pages that are linked to and
for all pages that are linked to and 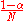 for all pages that are not linked to. The parameter
for all pages that are not linked to. The parameter  is taken to be about 0.85.
is taken to be about 0.85.
Markov models have also been used to analyze web navigation behavior of users. A user's web link transition on a particular website can be modeled using first- or second-order Markov models and can be used to make predictions regarding future navigation and to personalize the web page for an individual user.
Statistics
Markov chain methods have also become very important for generating sequences of random numbers to accurately reflect very complicated desired probability distributions, via a process called Markov chain Monte CarloMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
(MCMC). In recent years this has revolutionized the practicability of Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
methods, allowing a wide range of posterior distributions to be simulated and their parameters found numerically.
Economics and finance
Markov chains are used in Finance and Economics to model a variety of different phenomena, including asset prices and market crashes. The first financial model to use a Markov chain was from Prasad et al. in 1974. Another was the regime-switching model of James D. HamiltonJames D. HamiltonJames Douglas "Jim" Hamilton is an US econometrician currently teaching at University of California, San Diego. His work is especially influential in time series and energy economics...
(1989), in which a Markov chain is used to model switches between periods of high volatility and low volatility of asset returns. A more recent example is the Markov Switching MultifractalMarkov switching multifractalIn financial econometrics, the Markov-switching multifractal is a model of asset returns that incorporates stochastic volatility components of heterogeneous durations. MSM captures the outliers, log-memory-like volatility persistence and power variation of financial returns...
asset pricing model, which builds upon the convenience of earlier regime-switching models. It uses an arbitrarily large Markov chain to drive the level of volatility of asset returns.
Dynamic macroeconomics heavily uses Markov chains. An example is using Markov chains to exogenously model prices of equity (stock) in a general equilibriumGeneral equilibriumGeneral equilibrium theory is a branch of theoretical economics. It seeks to explain the behavior of supply, demand and prices in a whole economy with several or many interacting markets, by seeking to prove that a set of prices exists that will result in an overall equilibrium, hence general...
setting.
Leontief's Input-output modelInput-output modelIn economics, an input-output model is a quantitative economic technique that represents the interdependencies between different branches of national economy or between branches of different, even competing economies. Wassily Leontief developed this type of analysis and took the Nobel Memorial...
is a Markov chain.
Social sciences
Markov chains are generally used in describing path-dependent arguments, where current structural configurations condition future outcomes. An example is the commonly argued link between economic developmentEconomic developmentEconomic development generally refers to the sustained, concerted actions of policymakers and communities that promote the standard of living and economic health of a specific area...
and the rise of capitalismCapitalismCapitalism is an economic system that became dominant in the Western world following the demise of feudalism. There is no consensus on the precise definition nor on how the term should be used as a historical category...
. Once a country reaches a specific level of economic development, the configuration of structural factors, such as size of the commercial bourgeoisieBourgeoisieIn sociology and political science, bourgeoisie describes a range of groups across history. In the Western world, between the late 18th century and the present day, the bourgeoisie is a social class "characterized by their ownership of capital and their related culture." A member of the...
, the ratio of urban to rural residence, the rate of political mobilization, etc., will generate a higher probability of transitioning from authoritarian to capitalist.
Mathematical biology
Markov chains also have many applications in biological modelling, particularly population processPopulation processIn applied probability, a population process is a Markov chain in which the state of the chain is analogous to the number of individuals in a population , and changes to the state are analogous to the addition or removal of individuals from the population.Although named by analogy to biological...
es, which are useful in modelling processes that are (at least) analogous to biological populations. The Leslie matrixLeslie matrixIn applied mathematics, the Leslie matrix is a discrete, age-structured model of population growth that is very popular in population ecology. It was invented by and named after Patrick H. Leslie...
is one such example, though some of its entries
are not probabilities (they may be greater than 1). Another example is the modeling of cell shape in dividing sheets of epithelial cells. Yet another example is the state of Ion channelIon channelIon channels are pore-forming proteins that help establish and control the small voltage gradient across the plasma membrane of cells by allowing the flow of ions down their electrochemical gradient. They are present in the membranes that surround all biological cells...
s in cell membranes.
Markov chains are also used in simulations of brain function, such as the simulation of the mammalian neocortex.
Games
Markov chains can be used to model many games of chance. The children's games Snakes and LaddersSnakes and laddersSnakes and Ladders is an ancient Indian board game regarded today as a worldwide classic. It is played between two or more players on a game board having numbered, gridded squares. A number of "ladders" and "snakes" are pictured on the board, each connecting two specific board squares...
and "Hi Ho! Cherry-OHi Ho! Cherry-OHi Ho! Cherry-O is a children's board game currently published by Milton Bradley in which two to four players spin a spinner in an attempt to collect cherries. The original edition, designed by Hermann Wernhard and first published in 1960 by Whitman Publishers , had players compete to collect 10...
", for example, are represented exactly by Markov chains. At each turn, the player starts in a given state (on a given square) and from there has fixed odds of moving to certain other states (squares).
Music
Markov chains are employed in algorithmic music compositionAlgorithmic compositionAlgorithmic composition is the technique of using algorithms to create music.Algorithms have been used to compose music for centuries; the procedures used to plot voice-leading in Western counterpoint, for example, can often be reduced to algorithmic determinacy...
, particularly in software programs such as CSoundCsoundCsound is a computer programming language for dealing with sound, also known as a sound compiler or an audio programming language, or more precisely, a C-based audio DSL. It is called Csound because it is written in C, as opposed to some of its predecessors...
or MaxMax (software)Max is a visual programming language for music and multimedia developed and maintained by San Francisco-based software company Cycling '74. During its 20-year history, it has been widely used by composers, performers, software designers, researchers, and artists for creating innovative recordings,...
or SuperColliderSupercolliderA Supercollider is a high energy particle accelerator. The term may refer to:* Superconducting Super Collider, planned 80 km project in Texas, canceled in 1993...
. In a first-order chain, the states of the system become note or pitch values, and a probability vectorProbability vectorStochastic vector redirects here. For the concept of a random vector, see Multivariate random variable.In mathematics and statistics, a probability vector or stochastic vector is a vector with non-negative entries that add up to one....
for each note is constructed, completing a transition probability matrix (see below). An algorithm is constructed to produce and output note values based on the transition matrix weightings, which could be MIDI note values, frequency (HzHertzThe hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
), or any other desirable metric.
1st-order matrix Note A C♯ E♭ A 0.1 0.6 0.3 C♯ 0.25 0.05 0.7 E♭ 0.7 0.3 0
2nd-order matrix Note A D G AA 0.18 0.6 0.22 AD 0.5 0.5 0 AG 0.15 0.75 0.1 DD 0 0 1 DA 0.25 0 0.75 DG 0.9 0.1 0 GG 0.4 0.4 0.2 GA 0.5 0.25 0.25 GD 1 0 0
A second-order Markov chain can be introduced by considering the current state and also the previous state, as indicated in the second table. Higher, nth-order chains tend to "group" particular notes together, while 'breaking off' into other patterns and sequences occasionally. These higher-order chains tend to generate results with a sense of phrasalPhrase (music)In music and music theory, phrase and phrasing are concepts and practices related to grouping consecutive melodic notes, both in their composition and performance...
structure, rather than the 'aimless wandering' produced by a first-order system.
It should also be noted that Markov chains can be used structurally, as in Xenakis's Analogique A and B, as described in his book 'Formalized Music: Mathematics and Thought in Composition'
Baseball
Markov chain models have been used in advanced baseball analysis since 1960, although their use is still rare. Each half-inning of a baseball game fits the Markov chain state when the number of runners and outs are considered. During any at-bat, there are 24 possible combinations of number of outs and position of the runners. Mark Pankin shows that Markov chain models can be used to evaluate runs created for both individual players as well as a team.
He also discusses various kinds of strategies and play conditions: how Markov chain models have been used to analyze statistics for game situations such as buntingBuntingBunting can refer to:* Bunting , a group of birds* An infant sleeping bag* The act of laying down a bunt, a type of offensive play in baseball* Bunting , a lightweight cloth material often used for flags and festive decorations...
and base stealing and differences when playing on grass vs. astroturfAstroTurfAstroTurf is a brand of artificial turf. Although the term is a registered trademark, it is sometimes used as a generic description of any kind of artificial turf. The original AstroTurf product was a short pile synthetic turf while the current products incorporate modern features such as...
.
Markov text generators
Markov processes can also be used to generate superficially "real-looking" text given a sample document: they are used in a variety of recreational "parody generator" software (see dissociated pressDissociated pressDissociated press is an algorithm for generating text based on another text. It is intended for transforming any text into potentially humorous garbage. The name is a play on "Associated Press".An implementation of the algorithm is available in Emacs....
, Jeff Harrison http://www.fieralingue.it/modules.php?name=Content&pa=list_pages_categories&cid=111, Mark V ShaneyMark V ShaneyMark V Shaney is a fake Usenet user whose postings were generated by using Markov chain techniques. The name is a play on the words "Markov chain". Many readers were fooled into thinking that the quirky, sometimes uncannily topical posts were written by a real person.-History:Bruce Ellis did the...
).
These processes are also used by spammersE-mail spamEmail spam, also known as junk email or unsolicited bulk email , is a subset of spam that involves nearly identical messages sent to numerous recipients by email. Definitions of spam usually include the aspects that email is unsolicited and sent in bulk. One subset of UBE is UCE...
to inject real-looking hidden paragraphs into unsolicited email in an attempt to get these messages past spam filters.
Fitting
When fitting a Markov chain to data, situations where parameters poorly describe the situation may highlight interesting trends.
History
Andrey MarkovAndrey MarkovAndrey Andreyevich Markov was a Russian mathematician. He is best known for his work on theory of stochastic processes...
produced the first results (1906) for these processes, purely theoretically.
A generalization to countably infinite state spaces was given by Kolmogorov (1936).
Markov chains are related to Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
and the ergodic hypothesisErgodic hypothesisIn physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...
, two topics in physics which were important in the early years of the twentieth century, but Markov appears to have pursued this out of a mathematical motivation, namely the extension of the law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
to dependent events. In 1913, he applied his findings for the first time to the first 20,000 letters of Pushkin's Eugene OneginEugene OneginEugene Onegin is a novel in verse written by Alexander Pushkin.It is a classic of Russian literature, and its eponymous protagonist has served as the model for a number of Russian literary heroes . It was published in serial form between 1825 and 1832...
.
Seneta provides an account of Markov's motivations and the theory's early development. The term "chain" was used by Markov (1906).
See also
- Hidden Markov modelHidden Markov modelA hidden Markov model is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E...
- Telescoping Markov chainTelescoping Markov chainIn probability theory, a telescoping Markov chain is a vector-valued stochastic process that satisfies a Markov property and admits a hierarchical format through a network of transition matrices with cascading dependence....
- Markov chain mixing timeMarkov chain mixing timeIn probability theory, the mixing time of a Markov chain is the time until the Markov chain is "close" to its steady state distribution.More precisely, a fundamental result about Markov chains is that a finite state irreducible aperiodic chain has a unique stationary distribution π and,...
- Markov chain geostatisticsMarkov chain geostatisticsMarkov chain geostatistics refer to the Markov chain models, simulation algorithms and associated spatial correlation measures based on the Markov chain random field theory, which extends a single Markov chain into a multi-dimensional field for geostatistical modeling. A Markov chain random field...
- Quantum Markov chainQuantum Markov chainIn mathematics, the quantum Markov chain is a reformulation of the ideas of a classical Markov chain, replacing the classical definitions of probability with quantum probability...
- Markov processMarkov processIn probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
- Markov information sourceMarkov information sourceIn mathematics, a Markov information source, or simply, a Markov source, is an information source whose underlying dynamics are given by a stationary finite Markov chain.-Formal definition:...
- Markov chain Monte CarloMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
- Markov networkMarkov networkA Markov random field, Markov network or undirected graphical model is a set of variables having a Markov property described by an undirected graph. A Markov random field is similar to a Bayesian network in its representation of dependencies...
- Markov blanketMarkov blanketIn machine learning, the Markov blanket for a node A in a Bayesian network is the set of nodes \partial A composed of A's parents, its children, and its children's other parents. In a Markov network, the Markov blanket of a node is its set of neighbouring nodes...
- Semi-Markov processSemi-Markov processA continuous-time stochastic process is called a semi-Markov process or 'Markov renewal process' if the embedded jump chain is a Markov chain, and where the holding times are random variables with any distribution, whose distribution function may depend on the two states between which the move is...
- Variable-order Markov modelVariable-order Markov modelVariable-order Markov models are an important class of models that extend the well known Markov chain models. In contrast to the Markov chain models, where each random variable in a sequence with a Markov property depends on a fixed number of random variables, in VOM models this number of...
- Markov decision processMarkov decision processMarkov decision processes , named after Andrey Markov, provide a mathematical framework for modeling decision-making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying a wide range of optimization problems solved via...
External links
- Techniques to Understand Computer Simulations: Markov Chain Analysis
- Markov Chains chapter in American Mathematical Society's introductory probability book(pdf)
- Markov Chains
- Chapter 5: Markov Chain Models
- A JavaScript Markovian text compressor (in Portuguese).
- Application to Markov Chains
- Generating Text:Section 15.3 of Programming Pearls
- Generating Text Online: Markov Random Walk v1.1
- a list of recourses related to Markov chains